Спосіб визначення коефіцієнта тертя між гнучким тілом та барабаном

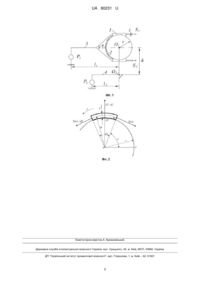
Реферат: UA 80231 U UA 80231 U 5 10 15 Корисна модель належить до техніки випробування матеріалів, зокрема до способів визначення фрикційних характеристик гнучких тіл, а саме коефіцієнта тертя між гнучким тілом та барабаном. В техніці випробування матеріалів відомий спосіб визначення коефіцієнта тертя між тілами в одній площині, які ковзають між собою, при заданій нормальній реакції між ними у відповідності з законом Амонтона (Леонардо да Вінчі) [Колчин Н.И. Механика машин. Т2. Кинетостатика и динамика машин. Трение в машинах. / Колчин Н.И. - Л.: Машиностроение, 1972.-456 с.]. Недоліком цього способу є те, що спосіб не забезпечує достовірності визначення коефіцієнта тертя гнучких тіл при терті по циліндричній поверхні. Найближчим технічним рішенням є спосіб визначення коефіцієнта тертя між гнучким тілом та барабаном, які ковзають між собою, що включає визначення зусиль натягування гнучкого тіла в набігаючій та збігаючій з барабана ланках, кута обхвату гнучким тілом барабана, лінійної маси та швидкості руху гнучкого тіла при відомому моменті гальмування барабана, а коефіцієнт тертя визначають у відповідності з законом тертя гнучких тіл Ейлера [Колчин Н.И. Механика машин. Т2. Кинетостатика и динамика машин. Трение в машинах. / Колчин Н.И. - Л.: Машиностроение, 1972.-456 с.] по формулі f 20 25 30 35 40 45 50 55 1 S  2  q  2  ln 1 ,  S2  2  q   2 де f - коефіцієнт тертя гнучкого тіла; S2, S1 - зусилля натягування гнучкого тіла в набігаючій та збігаючій з барабана ланках;  - кут обхвату гнучким тілом барабана;  - швидкість ковзання гнучкого тіла; q - лінійна маса гнучкого тіла. Недоліком цього способу є недостовірність визначення коефіцієнта тертя між гнучким тіла та барабана із-за того, що при його розрахунках використовується відомий закон тертя гнучких тіл Ейлера, який поширюється лише на тертя ідеальної нитки по нерухомому блоці, враховує застарілі уявлення про тертя Амонтона та були невідомі принципи збереження енергії, що діяло в час виведення закону. В основу корисної моделі поставлено задачу удосконалення способу визначення коефіцієнта тертя між гнучким тілом та барабаном, в якому досягається можливість врахування фактичного впливу нормальної реакції між тілами, сучасних знань про тертя та принципу збереження енергії, геометричних розмірів та конструкції гнучкого тіла і за рахунок цього підвищується достовірність визначення параметра. Поставлена задача вирішується тим, що в способі визначення коефіцієнта тертя між гнучким тілом та барабаном згідно з винаходом попередньо задають величину сумарного зусилля натягування в набігаючій та збігаючій з барабана ланках, визначають радіуси барабана та кривизни гнучкого тіла в зоні тертя по якій сконцентрована рівнодіюча зусилля натягування, а коефіцієнт тертя визначають з виразу  2  (S1  S2 ) f  , r   (S1  S2  2  q   2 ) де f - коефіцієнт тертя гнучкого тіла; S2, S1 - зусилля натягування гнучкого тіла в набігаючій та збігаючій з барабана ланках;  - кут обхвату гнучким тілом барабана;  - швидкість ковзання гнучкого тіла; q - лінійна маса гнучкого тіла, r - радіус барабана;  - радіус кривизни гнучкого тіла, по якій сконцентрована рівнодіюча зусилля натягування На фіг. 1 представлена схема визначення зусилля натягування гнучкого тіла в набігаючій та збігаючій з барабана ланках заданого перетину: де 1 - стрічкове гальмо; 2 - барабан натяжної станції короткого конвеєра; 3, 4 - важелі; Р1, Р2 - динамометри; S2, S1 - зусилля натягування гнучкого тіла в набігаючій та збігаючій з барабана ланках конвеєрної стрічки; t – товщина гнучкого тіла (Привідний барабан короткого конвеєра відкинуто та замінено зусиллями S2, та S1). На фіг. 2. представлена елементарна ланка гнучкого тіла dl: де S() и [S()+dS] - сили натягування гнучкого тіла на кінцях елементарної ланки; dC - відцентрова сила елементарної ланки; dN - нормальна реакція між елементарною ланкою гнучкого тіла та барабаном; dF - сила тертя ковзання між елементарною ланкою гнучкого тіла і барабаном; h - товщина гнучкого тіла;  - радіус умовної (нейтральної) подовжньої лінії гнучкого тіла;  - кут перетину гнучкого тіла, який контактує з барабаном; da - елементарний кут на елементарній ланці гнучкого тіла. Спосіб реалізується таким чином. Спочатку (фіг. 1) попередньо за допомогою динамометра Р2 та важеля 4, на якому розташовується кінцевий барабан 2, задається зусилля натягування конвеєрної стрічки 1 UA 80231 U (величина сумарного зусилля натягування гнучкого тіла в набігаючій та збігаючій з барабана ланках конвеєрної стрічки S2+S1), яка практично дорівнює подвійній сумі частки нормальної реакції між тілами та кута обхвату і добутку лінійної маси гнучкого тіла на квадрат її швидкості 5 10 N  S1  S2  2    q   2 ,     де N - нормальна реакція між тілами. Привідним барабаном запускається конвеєр і поступово за допомогою стрічкового гальма І створюється на валу кінцевого барабана 2 момент гальмування, при якому він гальмується чи зупиняється. При цьому визначається показник динамометра Р2 на важелі 3, який контролює силу тертя, що виникає між тілами. Рівнодіюча внутрішніх сил натягування стрічки в зоні контакту тіл діє по кривизні з радіусом  . Методами механіки з умови рівноваги механічної системи визначаються зусилля натягування гнучкого тіла в набігаючій та збігаючій з барабана ланках S2, S1 за формулами P  l    P1  l1  h S1  2 2 ; 2 h P2  l2    P1  l1  h . 2 h В разі симетричного по середній лінії перетину гнучкого тіла з одного матеріалу та укріпленого (армованого) по ній більш міцним матеріалом (наприклад, конвеєрна стрічка укріплена тросом чи тканою прокладкою) радіус кривизни , по якій зосереджена рівнодіюча сил натягування, співпадає з середньою лінією. Про це свідчать, зокрема, результати досліджень діаметра гнучких резинових кілець [Лубенец Н.А. Обоснование метода измерения диаметров резиновых уплотнительных колец / Лубенец Н.А., Панин В.В., Сафронов Е.В. // Производство шин, резинотехнических и асбестотехнических изделий. - М., 1983. - № 11. - С. 16-19.]. В іншому випадку (наприклад, клиновий ремінь) радіус кривизни  , по якій зосереджена рівнодіюча сил натягування, залежить ще і від форми перетину [Андреев А.В. Передача трением / Андреев А.В. - М.: Машгиз, 1978.-176с]. Тому радіус кривизни  визначається з умови одного розтягування під дією середньої сумарної величини зусилля в набігаючій та збігаючій з барабана лінійної ланки гнучкого тіла та цієї ж ланки, перекинутої через барабан, яка, зокрема, S  S2 має задану криволінійну траєкторію (задану циліндричну кривизну), рівного 1 . 2 Розшукуваний коефіцієнт тертя визначають з виразу  2  (S1  S2 ) f  , r   (S1  S2  2  q   2 ) Для обґрунтування виразу розглянемо розрахункову схему фіг. 2. Система рівнянь рівноваги сил, моментів і закону тертя тіл Кулона для елементарної ланки гнучкого тіла dl, який відповідає елементарному куту обхвату d, при ковзанні гнучкого тіла по блоку буде S2  15 20 25 30 dN  S()  d  dC  S()  d  q  2    d;  r  dF    d; 35 40 Fc    d  tg  dN; r  де Fc - сила тертя між гнучким тілом та барабаном при нормальній реакції, яка дорівнює нулю; tg - тангенс кута нахилу залежності сили тертя від нормальної реакції між тілами. Тому диференційне рівняння має вид F  dF   dS  c  d  tg  (S()  q  2 )  d. r  Його розв'язання dF  S  F   1   dS    c  tg  (S()  q  2 )  d. r S   0 1 2 UA 80231 U Інтеграл   S()  d, який входе в отримане рівняння (площа фігури, яка обмежена функцією 0 5 S() в межах кута обхвату ) - нормальна реакція між гнучким тілом та барабаном, яка обумовлена тільки натягуванням гнучкого тіла. У відповідності з принципом збереження потенціальної енергії подовження лінійнодеформованого гнучкого тіла при заданому зусиллі натягування не залежить від його фрикційних властивостей lk  10  1 б 1 б S(, f )    (, f )  dl     dl   S(, f )  d  const, E а E а F EF 0 де, lk - подовження ланки лінійно-деформованого гнучкого тіла, який контактує з барабаном; Е - модуль Юнга гнучкого тіла; F - площа перетину гнучкого тіла; (, f ) - поздовжнє напруження у гнучкому тілі; а, б - початок та кінець лінії контакту між тілами. При цьому інтеграл   S(, f )  d в приведеному виразі також величина постійна. Але це 0 15 можливо тільки при лінійній залежності розшукуваного натягування гнучкого тіла S() в зоні тертя 2 S  S2 S()  1    S2.  Тоді сумарна нормальна реакція між гнучким тілом та барабаном, обумовлена натягуванням гнучкого тіла та його відцентровими силами складе   S  S2  2  q  2  . N   (S() q  2 )  d     1   2 0   Звідки 20 N  S1  S2  2    q   2 .     Розв'язанням диференційного рівняння буде   S  S2  2  q   2  tg  (S()  q   2 )  d  Fc  tg    ( 1 ). 2  0 Або з використанням коефіцієнта тертя   (S1  S2 )  r 25 30 35  Fc    S  S2  2  q  2  (S1  S2 )  f    ( 1 ). r 2 Чи  2  (S1  S2 ) f  . r   (S1  S2  2  q   2 ) Для визначення сили тертя між гнучким тілом та барабаном попередньо задають величину сумарного зусилля натягування в набігаючій та збігаючій з барабана ланках S2 та S1, яке дорівнює подвійній сумі частки нормальної реакції між тілами та кута обхвату і добутку лінійної маси гнучкого тіла на квадрат її швидкості N  S1  S2  2    q   2 ,     Це відповідає заданій нормальній реакції між тілами, що погоджується з пануючим зараз законом тертя тіл Кулона. В таблиці приведено дані експериментальної оцінки коефіцієнта тертя нарізної резинотканої конвеєрної стрічки загального призначення з лінійною масою 7,6 кг/м та товщиною 10 мм по барабану короткого конвеєра при швидкості пересування 1 м/с (фіг. 1). Параметри конвеєра: l1=0,92 м; l2=1,52 м; r=0,11 м; h=0,39 м;  - 3,14 рад. 3 UA 80231 U Таблиця Дані експериментальної оцінки коефіцієнта тертя різними способами Стан стрічки Параметри, кГ Коефіцієнт тертя Р1 Суха Волога 5 10 15 20 25 30 Р2 S1 S2 1 S  2  q  2  ln 1  S2  2  q   2 2  (S1  S 2 )   r   (S1  S 2  2  q   2 ) 24 9 80 80 256 193 55 118 0,53 0,17 0,43 0,16 Отримані результати коефіцієнта тертя конвеєрної стрічки згідно з прототипом в порівнянні з істинним значенням завищені приблизно до 20 %, що відповідає загальній різниці між результатами визначення сили тертя, отриманими з використанням закону тертя гнучких тіл Ейлера та їх істинними значеннями, котрі інколи досягають 30 % [Андреев А.В. Передача трением / Андреев А.В. - М.: Машгиз, 1978.-176 с.], і свідчить про достовірність запропонованого способу. Запропонований спосіб в порівняння з відомим (прототипом) сприяє підвищенню достовірності визначення коефіцієнта тертя гнучкого тіла по барабану, що дозволить приблизитись до визначення його істинного значення в умовах тертя гнучкого тіла по барабану з заданою нормальною реакцією. ФОРМУЛА КОРИСНОЇ МОДЕЛІ Спосіб визначення коефіцієнта тертя між гнучким тілом та барабаном, що включає визначення зусиль натягування гнучкого тіла в набігаючій та збігаючій з барабана ланках, кута обхвату гнучким тілом барабана, лінійної маси та швидкості руху гнучкого тіла в умовах створення моменту гальмування на валу барабана, який відрізняється тим, що попередньо задають величину сумарного зусилля натягування в набігаючій та збігаючій з барабана ланках, визначають радіуси барабана та кривизни гнучкого тіла в зоні тертя, по якій сконцентрована рівнодіюча зусилля натягування, а коефіцієнт тертя визначають з виразу 2  (S1  S2 )  f  , r   (S1  S2  2  q   2 ) де f - коефіцієнт тертя гнучкого тіла; S2 , S1 - зусилля натягування гнучкого тіла в набігаючій та збігаючій з барабана ланках; r - радіус барабана;  - радіус кривизни гнучкого тіла, по якій сконцентрована рівнодіюча зусилля натягування;  кут обхвату гнучким тілом барабана;  - швидкість ковзання гнучкого тіла; q - лінійна маса гнучкого тіла. 4 UA 80231 U Комп’ютерна верстка А. Крижанівський Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601 5