Спосіб автоматичного керування нелінійним об’єктом

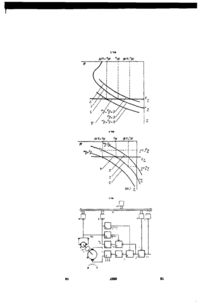
Спосіб автоматичного керування нелінійним об'єктом, який полягає в тому, що вимірюють регульовану координату, отриманий сигнал порівнюють з сигналом завдання, результат порівняння підсумовують з сигналом компенсації' нелінійності, який відрізняється тим, що результат порівняння перетворюють в пропорційний сигнал на виході моделі, результат перетворення масштабують і алгебраїчно підсумовують з сигналом керування, вимірюють сигнал завдання, сигнал пропорційний регульованій координаті і сигнал на виході моделі, визначають значення нелінійної складової регульованої координати по збуренню і визначають величину сигналу компенсації зовнішнього збурення згідно виразу: £M = biU 2 +biU M -£3. сигнал завдання алгебраїчно підсумовують з сигналом компенсації і формують сигнал, пропорційний заданому значенню регульованої координати, де: Єз - сигнал завдання; £м - сигнал компенсації; U z - сигнал, пропорційний регульованій координаті; UM - сигнал з виходу моделі; Ь-і, D2 - постійні коефіцієнти. Спосіб корисної моделі відноситься до галузі автоматичного керування і регулювання і може використовуватися для стабілізації координат об'єктів з нелінійної залежності між регулюємою координатою та зовнішнім збуренням. Відомий спосіб автоматичного керування нелінійним об'єктом, який полягає в лінеаризації' нелінійної характеристики об'єкта та керування нелінійним об'єктом, як лінійним [1]. Недоліками цього способу є наявність статичної похибки регулювання та вузький діапазон керуючих впливів, визначений лінеаризованою ділянкою. Відомий спосіб автоматичного керування нелінійним об'єктом, який полягає в тому, що формують сигнал, пропорційний регулюємій координаті, одержану величину зрівнюють з заданим і формують сигнал керування пропорційний отриманій різниці, при цьому задану величину визначають, виходячи з результуючої статичної характеристики системі керування [2]. Недоліком даного способу є статична похибка регулювання, яка визначається не лінійністю результуючої характеристики. Відомий спосіб автоматичного керування нелінійним об'єктом, який полягає в тому, що форму ють сигнал, пропорційний регулюємій координаті, одержану величину зрівнюють з сигналом завдання, а результат порівняння сумують з сигналом компенсації не лінійності [3], прототип. Недоліком відомого способу є те, що для компенсації не лінійності потрібно синтезувати пропорційно-диференціальний регулятор, який реалізує нелінійну функцію, обернену до не лінійності об'єкта регулювання. Крім того, навіть при досягненні лінійності об'єкта регулювання отримана система має статичну похибку. Ще один недолік відомого способу полягає в тому, що в замкненій системі автоматичного регулювання з від'ємним зворотнім зв'язком зменшується коефіцієнт підсилення прямого перетворення в і -г К|-|К 0 разів, що знижує ефективність регулювання. Задачею заявленого об'єкта є підвищення точності керування за рахунок виключення статичної похибки. Поставлена задача вирішується тим, в способі керування нелінійним об'єктом, який полягає в тому що вимірюють регулюєму координату, отриманий сигнал порівнюють з сигналом завдання, ео ю со 6507 результат порівняння сумують з сигналом компенсації не лінійності, результат порівняння перетворюють в пропорційний сигнал на виході моделі, результат перетворення масштабують і алгебраїчно сумують з сигналом керування, вимірюють сигнал завдання, сигнал пропорційний регулюємій координаті і сигнал на виході моделі, визначають значення нелінійної складовою регулюємої координати по збуренню і визначають величину сигналу компенсації зовнішнього збурення згідно виразу єм =Ь1и2+Ь2им-є3 Сигнал завдання алгебраїчне сумують з сигналом компенсації зовнішнього збурення, а сигнал, пропорційний заданому значенню регулюємої координати формують, як алгебраїчну суму сигналу компенсації зовнішнього моменту і сигналу завдання в відповідності з заданим законом керування. Де: є 3 - сигнал завдання наті є м - сигнал компенсації U z - сигнал, пропорційний регулюємій коорди UM - сигнал з виходу моделі Ьі,Ьг - постійні коефіцієнти На Фіг.1 приведена структурна схема системи для втілення способу. На Фіг.2, схема системи автоматичного регулювання нелінійним об'єктом в якій блоки 3,8,9 та 10 реалізовані програмним шляхом в процесорі. На Фіг.З приведений приклад принципового виконання способу. На Фіг.4 приклад статичних характеристик регулювання з вогнутою не лінійністю. На Фіг.5 приклад статичних характеристик з випуклою не лінійністю. На Фіг.6 ілюстрація розрахункового прикладу. На Фіг.7-9 приклад накладання шуму на зовнішнє збурення. Система автоматичного регулювання нелінійного об'єкта Фіг.1 містить перший, другий та третій 1 , 2 і З суматори, підсилювач 4, регулятор 5, нелінійний об'єкт 6, вимірювач значення регулюємої координати 7, модель 8 в якості якої може використовуватися лінійний підсилювач, перший і другий 9, 10 масштабні перетворювачі, перший, другий та третій 11, 12 та 13 модулі вводу аналогових сигналів (аналого-цифрові перетворювачі) АЦП, модуль виводу 14 (цифро-аналоговий перетворювач) ЦАП, інтерфейс 15, процесор 16. Блоки 2-10 утворюють контур статичного регулювання і виконують роль контуру підлеглого регулювання. Блоки 1, 11, 13, інтерфейс 15 та процессор 16 утворюють контур астатичного регулювання і виконують роль основного контуру регулювання. Спосіб автоматичного регулювання нелінійним об'єктом виконується наступним чином. Рівняння статичної характеристики нелінійного об'єкта визначається наступною залежністю Z = K u u-F(M) (1). де: u - сигнал керування М - збурення регулюємої величини Ки - коефіцієнт передачі прямого перетворен ня, що включає в себе блоки 4, 5, 6. 2 n F(M) = аіМ + а2М і +... + a n M - поліном п-го ступеня який визначає нелінійну характеристику регулювання. аі,а2...ап - коефіцієнти полінома які визначаються із системи рівнянь: 11 + а 2 М^ +... + арМ , = 2 0 - 2 ! | + ... + апМ£ = 2 0 - 2 2 J-+... + a n M ; ; = Z 0 - Z n (2) де: 2о - значення регулюємої координати при М=0, Фіг.2, 3. п - порядок полінома. Для втілення запропонованого способу формують сигнал є пропорційний заданому значенню регулюємої координати, вимірюють значення регулюємої координати у відповідності з рівнянням: U z = KZ2 (3) де: U2 - сигнал на виході вимірювача регулюємої координати 2; Kz - коефіцієнт пропорційності Для здійснення способу використовується модель 8 з функцією перетворення U M = Кміїм, (4) де: им - сигнал на вході моделі; UM - сигнал на виході моделі; Км - коефіцієнт перетворення. Далі, отриманий сигнал масштабують і сумують з сигналом, пропорційним регулюємій величині і формують сигнал на виході моделі у відповідності з рівнянням: U M = K M ( £ - K Z ( 3 2 ) (5) де: є - сигнал на вході суматора 3; UM - сигнал на виході моделі; Км - коефіцієнт передачі моделі; Р - коефіцієнт передачі масштабного перетворювача 9. Вихідний сигнал моделі масштабують і сумують з сигналом є, підсилюють в підсилювачі 3 і формують сигнал керування об'єктом у відповідності з рівнянням: де: u - сигнал на виході суматора 2; Ку - коефіцієнт підсилення; Рм - коефіцієнт передачі масштабного перетворювача 10. На основі (3) - (6) отримують систему двох координатне взаємопов'язаних рівнянь: 2 + K u p M U M = K u e - F ( M ) (7) -Kup*2 + U M = K M e (8) Систему можна виразити у вигляді матриці: 2 Г им L о J (9) Розв'язуючи систему (9) відносно сигналів 2 і UM І збурення F(M) отримують систему двох параметрично взаємопов'язаних рівнянь: ) (Ю) 6507 =K M ( I + KUP )E + P K M F ( M ) Рівняння (10) - (11) визначають рефлексивне керування об'єктом, коли модель взаємодіє з об'єктом таким чином, що об'єкт впливає на модель, а модель впливає на об'єкт. Причому внаслідок такої взаємодії збурення не діє на модель але сигнал на виході моделі містить складову, пропорційну збуренню яке діє на об'єкт, причому таким чином, що при збільшення збурення регулюєма координата зменшується, а сигнал на виході моделі збільшується і навпаки. Модель 8 називається рефлексивною, так як її перетворення (11) відображує перетворення нелінійного об'єкта (10). При виконанні умови: К и (3 = 1 (12) що легко досягається вибором коефіцієнта Р - тг~ масштабного перетворювача 10, рівняння к и (10) - (11) зводяться до вигляду: Z = K u e-F(M), (13) U M = K F F ( M ) , (14) ДЄ ^ F - є 3 + є м (15) З урахуванням рівняння (15), рівняння (9) (10) можна представити, у такому вигляді: U z = - K 0 ( e 3 + e M ) - K F F ( M ) (16) UM=-K де: К п = ^ кР = K UM К (Є З співвідношення (17) можна отримати рівнянє є ня інваріантно відносно сигналів з і м U Z + KFF(M) Ко UM-KFMF(M) : К Звідси визначають значення нелінійної складової збурення: KOUM-KUZ (20) F(M) = r+K0KFM Рівняння (20) можна представити в такому вигляді: F(M) = a 1 U M - a 2 U 2 (21) де: Ко KKF+K0KFM к KKF+K0KFM Враховуючи (21) рівняння (16) буде мати вигляд: - ^ З рівняння (10) випливає, що по запропонованому способу регулювання знаходиться на більш високому рівні ніж в прототипі, так, як нелінійна характеристика регулювання проходить через точку Z o = K u e що відповідає відсутності збурення та природної характеристики, що підвищує ефективність регулювання. З рівняння (12) випливає, що сигнал UM на виході моделі пропорційний збуренню яке діє на об'єкт регулювання і інваріантний відносно сигналу керування є. У відповідності з запропонованим способом сигнал є формують, як алгебраїчну суму сигналу завдання є з, пропорційного заданій регулюємій координаті і сигналу є м пропорційного зовнішньому збуренню. к = K0(£3+eM)-KFF(M) (11) к т (1-к ц р) FM Для знаходження величини є м сигналу компенсації зовнішнього збурення визначають відношення сигналів U z і UM: Звідки значення сигналу компенсації зовнішнього збурення є м визначають у відповідності з рівнянням: -—z ем = 1 м 2-^- (23) або e M = b 1 U z + b 2 U M - E 3 (24) де: 1 а к _ - 2 Ко Рівняння (21) і (24) реалізуються в процесорі 16. Результат обчислення є м виводиться через ЦАП 14. Система автоматичного регулювання працює наступним чином. Нехай до регулюємої координати прикладене зовнішнє збурення, яке відповідає деякому номінальному значенню Мн, поз. 1, Фіг.4 і 5. Значення регулюємої координати дорівнює Z3. В процесі регулювання відбувається неперервне вимірювання сигналу завдання є 3 , сигналу з виходу моделі UM І сигналу U z шляхом їх вводу через АЦП 11, 12 і 13 в процесор. При цьому коефіцієнти аі, аг, Ь-і, D2 зберігаються в пам'яті процесора у вигляді постійних коефіцієнтів. Зі зменшенням зовнішнього збурення на величину М Н - А М відбувається збільшення значення регулюємої координати на величину Z^+hZ. У процесі регулювання у процесорі 16 відбувається розрахунок значення діючого збурення F(M), у відповідності з рівнянням (20) і значення сигналу компенсації є м у відповідності з рівнянням (23). Отримане значення є через ЦАП 14 подається на 6507 другий вхід першого суматора 1 де зрівнюється з сигналом завдання є 3 і формується сигнал керування є , який подається на суматор 2 Фізично це означає паралельне зміщення регулюючої характеристики вправо, поз. З, що призводить до точного відновлення заданого значення регулюємої координати. Зі збільшенням зовнішнього збурення на величину М Н + А М відбувається зменшення регулюємої координати на величину Z g - A Z . Далі процеси регулювання відбуваються аналогічно вище викладеному, відбувається зміщення характеристики Z(M) вліво і відновлення регуюємої координати до заданої величини, поз. 2, Фіг 4, 5. Таким чином у ВІДПОВІДНОСТІ З запропонованим способом регулювання нелінійним об'єктом відбу 8 вається у ВІДПОВІДНОСТІ з ЛІНІЄЮ 4 паралельною до осі М, що свідчить про астатичне регулювання нелінійного об'єкта. Для доказу працездатності способу наведемо розрахунковий приклад. Нехай характеристика нелінійного об'єкта має вигляд: Z=10u-F(M) 2 3 де. F(M) = 43.2М + 0.89М - 0.0062М та вказана на Фіг.6, поз 1. Нехай U = 100, тоді: 2 Z = 1000 - F(M), a F(M) = 43.2М + 0.89М 3 0.0062М Нехай Kz = 0.01 Розрахункові значення цих величин наведено в таблиці 1 і наведені на Фіг.6 поз 1. Таблиця 1 М, Нм RM) Z Uz 0 0 1000 10,0 10 349,2 650,8 6,508 20 557,6 442,4 4,424 Нехай номінальне значення Мн = 20, що відповідає значенню регулюємої координати Z = 442,4 Задамо значення зміни збурення ±50%. Задамо наступні значення параметрів: Км = 10, р = 0.001, р м =0.1. Тоді будемо мати наступні рівняння: Z = 20e-F(M) U z =10e-0.01F(M) U M =10.1e-0.01F(M) ЗО 662,4 337,6 3,376 40 700,8 292,2 2,922 50 710,0 290,0 2,900 Отриману систему необхідно доповнити законом керування, тобто залежністю регулюємої координати від сигналу завдання. Нехай цей закон відповідає пропорційному у вигляді наступного рівняння* Z 3 = 8.848е3 Розрахункове значення цих рівнянь при є 3 = 50 наведені в таблиці 2 і показані на Фіг.6 поз. 1 Таблиця 2 м F(M) Z Uz UM 0 0 1000 10,0 505 10 349,2 650,8 6,508 501,508 20 557,6 442,4 4,424 499,424 Для визначення значень F(M) вимірюють сигнали Uz і UM: F(M) = 2.0202UM - 102.0202Uz При Мі = 20 отримують 0.2-499.424 + 10.1 4.424 V ' 0 1(1-0.1) При ЗМІНІ навантаження на ± 50, тобто при Мг = 10 та М 3 = ЗО будуть наступні значення: _ 0.2 501.508-10.1 6.508 _ г 0.099 F(M3)=°2498376-1013-376=6624 3 0.099 Для формування сигналу є м у ВІДПОВІДНОСТІ ЗІ знайденими значеннями F(M) діючого збурення будемо мати" ЗО 662,4 337,6 3,376 498,376 40 700,8 292,2 2,922 494,992 50 710,0 290,0 2,900 497,9 є м = 0.05соз -0.099U y +0 049F(M) ем1 = Є М2 £ 10.1 442.4-20 499.424 + 9.9 557.6 =0 100 2 1 01 -' мз = 10.1 442.4-20 501.508 + 9.9 349.2 = 10.42 202 10.1442.4-20 498.376 + 9.9 662.4 =5-24 Підставивши отримані значення в рівняння (16) отримаємо: щ = 20(50 + 0) - 557.6 = 442.4 (02 = 20(50 -10.42) - 349.2 = 442 4 «з = 20(50 + 5.24) - 662.4 = 442 4 Таким чином у ВІДПОВІДНОСТІ ДО запропонованого способу, зі зменшенням збурення сигнал завдання зменшується, а при збільшенні збурення 6507 10 збільшується, причому, на таку величину, що регулюєма координата залишається постійною Регулюючі характеристики для такого випадку показано на Фіг 4 поз 2 і 3 При ЗМІНІ сигналу завдання змінюють значення сигналу є 3 в рівнянні (22) Отже Z = 20(50+2 88) - 557 6 = 500 Приклад 2 Нехай сигнал є 3 представляє собою адитивну сполуку постійної складової і вузькополосної низькочастотної перешкоди у вигляді гармонічного сигналу е 3 = 5 0 + 5 siniOt Наприклад, потрібно при моменті зовнішнього Тоді будемо мати наступні перетворення навантаження М = 20 підтримувати регулюєму Z(t) = 20(50 +5sin10t) - F(M) координату на рівні Z3 = 500 Uz(t) = 0 2(50 +5sin10t) - 0 01F(M) Тоді маємо UM(t)=10 1(50+5sin10t)-0 01F(M) є м = 0 05 500-0 099 499 424 + 0.049 557.6 = 2 88 Розрахункові значення для цих рівнянь при М = 20 і ВІДПОВІДНО F(M) = 557 6 наведені в таблиці З Таблиця З t,MC e(t) Z(t) Uzft) UM(t) 0 50,0 442,4 4,424 499,324 5 53,830 519,0 5,190 538,107 10 54,929 540,88 5,408 549,156 З таблиці З можна зробити висновок, що як кутова швидкість ЕП, так і сигнали U z та UM мають крім постійної складової низькочастотну перешкоду, тоді F(M),=5 = 2 0202 • 538 107 -102 0202 • 5 190 = 557 6 F(M),=io = 2 0202 • 549 156 -102 0202 • 5 408 = 557 6 F(M),=15 = 2 0202 • 524 674 -102 0202 • 4 924 = 557 6 Сигнал е м буде визначатися наступними рівняннями є м і = 0 05 • 442 4 - 0 099 • 538 107 + 0 049 • 557 6 = -3 83 є м 2 = 0 05 • 442 4 - 0 099 • 549 156 + 0 049 • 557 6 = -4 924 е м з = 0 05 • 442 4 - 0 099 • 524 674 + 0 049 • 557 6 = -2 5 Звідси ZI = 20(53 83 - 3 83) - 557 6 = 442 4 15 52,50 492,40 4,924 524,674 20 48,289 408,18 4,081 482,142 25 45,075 343,54 3,435 449,681 30 45,669 355,78 3,557 455,68 Z2 = 20(54 924 - 4 924) - 557 6 = 442 4 Z2 = 20(52 5 - 2 5) - 557,6 = 442 4 Таким чином, при існуванні перешкоди у вхідному сигналі, система автоматичного керування формує сигнал, рівний по абсолютному значенню, але протилежний по знаку (противофазний) сигнал компенсації перешкоди, що підтверджує присутність властивості інваріантності рівнянь (23) та (28) відносно сигналу завдання Приклад 3 Розглянемо приклад динамічного характеру зміни моменту навантаження Наприклад, биття вала ЕП, тоді M(t) = 557 6+5sm10t Тоді ВІДПОВІДНІ перетворення матимуть вигляд U2(t) = 20e-557 6-5sin10t U M (t) = 0 2 е - 0 01(557 6 + 2sin10t) = = 10 1є-0 01(557 6 + 5sin10t) Результати розрахунку цих рівнянь наведено в таблиці 4 Таблиця 4 t мс , M(t), Н м Z(t) Uz(t) U M (t) 0 557 6 442 4 4 424 499 424 5 561 43 438 57 4 385 499 385 10 562 524 437 476 4 374 499 374 Тоді F(M)t=5 = 2 0202 • 499 385 - 102 0202 • 4 3857 = 561 430 F(M)t=io = 2 0202 • 499 374 - 102 0202 • 4 3747 = 562 524 F(M),=15 =2 0202 • 499 399 - 102 0202 • 4 399 = 560 10 отже е м і = 0 05 • 442 4 - 0 099 • 499 385 + 0 040 • 561 43 = 0 191 £ М 2 = 0 05 • 442 4 - 0 099 • 499 374 + 0 040 • 15 560 1 439 9 4 399 499 399 20 555 889 444 111 4 441 499 441 25 552 675 447 325 4 473 499 473 ЗО 553 269 446 731 4 467 499 467 562 524 = 0,246 є м з = 0 05 • 442 4 -0 099 • 499 399 + 0 040 • 560 1=0 125 звідки Zi =20(50+ 0 191)-561 43 = 442 4 Z2 = 20(50+0 246) - 561 524 = 442 4 Z 3 = 20(50+0 125) - 561 10 = 442 4 Результати розрахунку Z(t),Ta є к при динамічній ЗМІНІ навантаження M(t), з урахуванням наведених вище викладок наведено в таблиці 5 11 6507 12 Таблиця 5 t мс , M(t), Н м Z(t) 0 564.137 442.4 0,327 4 554,761 442.4 -0,142 2 561.607 442.4 0,2 Ці данні підтверджуються моделюванням результатів за допомогою програмного забезпечення Mathcad, результати у вигляді графіків наведені на Фіг.7 Наведені розрахункові приклади наочно підтверджують працездатність такого способу, а також досягнення позитивного ефекту, який полягає у відсутності статичної похибки, тобто у підвищенні точності регулювання при нелінійній характеристиці. Звичайно, усі теоретичні викладки, викладені у описанні винаходу у розділі підвищення точності 6 554,854 442.4 -0,137 10 559.027 442.4 0,071 регулювання відносяться також до об'єктів з лінійною характеристикою. Література: 1. Зайцев Г.Ф. Основы теории автоматического регулирования. Киев, Киевское высшее инженерное радиотехническое училище, 1974, с 437. 2. Юревич А. Н. Теория автоматического управления. - Ленинград, 1957, с. 175-176 3. Система регулирования нелинейного объекта. Авторское свидетельство СССР, №1679206, MI1KG05B 13/00, 1990. 1 \ ill 8 553,799 442.4 -0,190 і 1 4 /12 Є± Фіг. 1 Фіг. 2 Z0S9 6507 15 1200 1100 16 \ 1 . і Z(J^ 1000' \ Uі 900 \ \ dOC j і 2 K!\ V ; ьоо - 4/ b 700 1 600 \ \ 400 soo 200 100 ' ] 4 •£ = :.Q-b " ^ е-ы і ) Є" U ')—JO 42 І 1L J 30 і .0 , t' h) Н С Фіг.7 Фіг.8 Комп'ютерна верстка А. Крулевський Підписне Тираж 28 прим. Міністерство освіти і науки України Державний департамент інтелектуальної власності, вул. Урицького, 45, м Київ, МСП, 03680, Україна ДП "Український інститут промислової власності", вул Глазунова, 1, м. Київ - 4 2 , 01601