Завадостійкий n-входовий двійковий дешифратор

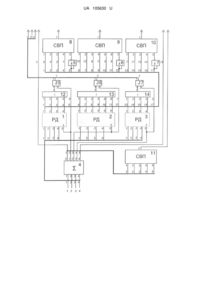
Реферат: UA 105630 U UA 105630 U Корисна модель належить до автоматики й обчислювальної техніки й може бути використана для дешифрації двійкових кодів в системах передачі даних, лічильниках, перетворювачів коду. Відомий завадостійкий n-входовий двійковий дешифратор, який містить суматор, n-1 схем 5 10 15 20 25 30 35 40 45 50 55 q рівноважних дешифраторів (далі РД) з n+1 входами і Cn (q  [1 ..., n  1]) виходами, де n , кількість входів двійкового завадостійкого двійкового дешифратора, q - можлива кількість одиниць у вхідній комбінації, і для виявлення частини помилок елементи АБО та схеми нерівнозначності. На входи кожного елементу АБО надходять сигнали з виходів відповідного РД. Вихід кожного елементу АБО з'єднаний з першим входом відповідної схеми нерівнозначності, на другий вхід якої подається сигнал з відповідного виходу суматора. Інформація про появу одиниці на виході схеми нерівнозначності свідчить про наявність помилки при роботі відповідного їй РД. Перші n входів кожного РД і всі n входів суматора з'єднані з n входами двійкового дешифратора, а n+1 - й вхід РД з відповідним виходом суматора одиниць. Цей пристрій найбільш близький до заявленого по технічній суті й досягнутому результату, тому він був обраний як прототип (Борисенко А.А., Лопатченко Б.К., Бражник И.Е. Построение экономичных дешифраторов, Сумы: Вісник СумДУ, № 10, 2006 г., с. 78, рис. 3). Недолік такого технічного рішення полягає в тому, що такий завадостійкий n-входовий двійковий дешифратор може виявляти лише частину помилок: появу однієї або більше одиниць на виходах РД, на n+1 вхід якого подається 0, та появу нулів на всіх виходах РД, на n+1 вхід якого подається 1. При цьому не виявляються дві або більше одиниць на виходах цього РД. Також такий двійковий дешифратор не може виявляти помилки на виході суматора. В основу корисної моделі поставлена задача вдосконалення існуючого завадостійкого дешифратора шляхом введення нового складу елементів та нової організації взаємозв'язків між ними, що забезпечило виявлення усіх помилок, за виключенням перестановок одиниць, на виходах рівноважних дешифраторів і на виході суматора, та можливість виявлення помилок в схемах виявлення помилок рівноважних дешифраторів, розширюючи таким чином функціональні можливості дешифратора. Поставлена задача вирішується тим, що в завадостійкий n-входовий двійковий дешифратор, що містить суматор, не більше n-1 схем рівноважних дешифраторів (далі РД) з (n+1) входами і q Cn (q  [1 ..., n  1]) виходами, де n - кількість входів завадостійкого двійкового дешифратора, q , можлива кількість одиниць у вхідній комбінації, елементи АБО та схеми нерівнозначності, перші n-входи кожного РД і всі n-входи суматора з'єднані з n-входами завадостійкого дешифратора, а (n+1)-й вхід РД - з відповідним виходом суматора, входи кожного елемента АБО зв'язані з виходами відповідного РД, а виходи з'єднані з першими входами відповідних схеми нерівнозначності, другий вхід яких зв'язаний з відповідним виходом суматора, згідно з корисною моделлю, в завадостійкий n-входовий двійковий дешифратор додатково введені (n-1) схем виявлення всіх помилок (СВП), входи кожної із яких з'єднані з виходами відповідних РД і виходами відповідних додатково введених інверторів, а виходи є виходами завадостійкого дешифратора, при цьому вхід кожного інвертора з'єднаний з виходом суматора, відповідним цьому РД, і кожна СВП має на один більше входів, ніж відповідний їй РД, і один вихід, окрім цього додатково введена СВП для суматора, n+1 входів якої з'єднуються з n+1 виходами суматора, а вихід є виходом завадостійкого дешифратора. Введення інвертора та СВП для всіх РД поряд з тим, що можна виявити появу однієї або більше одиниць на виходах РД, на n+1 вхід якого подається 0, та появу нулів на всіх виходах РД, на n+1 вхід якого подається 1, призводить до можливості виявляти дві або більше одиниць на виходах РД, на вхід якого подається 1, що призводить до підвищення завадостійкості. Крім того, частину помилок, яку виявляє СВП, виявляють елементи АБО та схеми нерівнозначності, що призводить до можливості виявляти помилки в схемах виявлення помилок РД. Введення додаткової СВП для суматора призводить до можливості виявляти всі помилки на виході суматора, за виключенням перестановок одиниць. Таким чином, введення вищезгаданих конструктивних елементів і зв'язків надає можливість виявляти всі помилки як на виходах рівноважних дешифраторів, так і на виході суматора, та можливість виявлення помилок в схемах виявлення помилок рівноважних дешифраторів, що значно розширює функціональні можливості самого дешифратора. На кресленні приведений дешифратор двійкового коду з довжиною комбінації n=4, і наведені наступні скорочення, а саме: - рівноважний дешифратор - "РД"; - суматор - "Σ"; - елементи АБО - "1"; 1 UA 105630 U 5 10 15 20 25 30 35 40 45 - схема нерівнозначності - "="; схема виявлення всіх помилок - "СВП"; інвертори виконані на основі елементів І-НЕ, які позначені як "&", з інверсією на своєму виході. Двійковий дешифратор містить, наприклад, n=4 входів, 2"=16 виходів до дешифрації вхідних комбінацій, n-1=3 невироджених РД (1, 2. 3), суматор (4). інверторів (5, 6, 7), СВП (8, 9, 10, 11), елементи АБО (12, 13, 14) та схеми нерівнозначності (15, 16, 17). q Як РД використані відомі схеми, які містять n+1 входів та C n виходів, які призначені до дешифрації комбінацій рівноважного коду з довжиною комбінації n і кількістю одиниць q, що подаються на перші n входів схеми. На n+1 подається сигнал, що дозволяє чи забороняє роботу схеми. Такі схеми представлені, наприклад, в (Борисенко Л.А., Лопатченко Б.К., Бражник И.Е. Построение экономичных дешифраторов, Сумы: Вісник СумДУ, № 10. 2006 г., с. 78, рис. 3). Як суматор використаний відомий матричний суматор, який видає одиничний сигнал, на одному з своїх виходів в залежності від кількості одиниць на своїх входах. Така схема представлена, наприклад, в (Борисенко Л.А., Лопатченко Б.К., Бражник И.Е. Построение экономичных дешифраторов, Сумы: Вісник СумДУ. № 10, 2006 г., с. 78, рис. 2). Комбінації двійкового коду розділені за кількістю одиниць від 0 до n. Для даної довжини кодової комбінації n=4 існують (n+1)=5 груп таких рівноважних комбінацій з кількістю одиниць q=0, 1, 2, 3, 4. Групам комбінацій з кількістю одиниць q=0, 4 не відповідають РД, оскільки до цих груп комбінацій входить тільки по одній комбінації, то РД, які б відповідали цих групам, були б виродженими, не містили б елементів і дешифрували б по одній комбінації, тому на кресленні виходи суматора 0 і 4 безпосередньо з'єднані з відповідно 0 і 15 виходами самого двійкового дешифратору. Групам комбінацій з кількістю одиниць q=1, 2, 3 відповідають РД (1, 2, 3). РД (1, q 2, 3) мають n+1=5 входів і C n виходів (q  [1 ..., n  1]) . Входи 1, 2, 3, 4 рівноважних , дешифраторів з'єднані з 1, 2, 3, 4 входами двійкового дешифратора, виходи всіх РД є виходами двійкового дешифратора. На вхід 5 рівноважних дешифраторів (1, 2, 3) подаються відповідно сигнали з виходів 1, 2, 3 суматора (4). Кожному РД (1, 2 або 3) відповідає один інвертор (5, 6, або 7), один елемент АБО (12, 13, 14), одна схема нерівнозначності (15, 16, 17) та одна СВП (8, 9 або 10). На входи інверторів (5, 6, 7) подаються сигнали з 1, 2, 3 виходів суматора (4). Кожна СВП (8, 9, 10) має на один більше входів, ніж кількість виходів у відповідному їй РД (1, 2, 3), та один вихід, що є виходом завадостійкого n-входового двійкового дешифратора. На входи кожної СВП (8, 9, 10) подаються сигнали з виходів відповідних РД (1, 2, 3) та з виходів відповідних інверторів (5, 6, 7). На входи кожного елемента АБО (12, 13, 14) подаються сигнали з виходів відповідного РД (1,2, 3). Виходи кожного елемента АБО (12, 13, 14) з'єднані з першим входом відповідної схеми нерівнозначності (15, 16, 17). На другий вхід цієї схеми подається сигнал з відповідного виходу суматора (4). На вхід СВП (11) подаються сигнали з виходів суматора (4), вихід СВП (11) є виходом завадостійкого n-входового двійкового дешифратора. В групу рівноважних комбінацій з кількістю одиниць q=0 входить лише одна комбінація: 0000. Цій групі рівноважних комбінацій не відповідає РД, оскільки він був би виродженим, не використовував би інформацію із своїх перших n входів, мав би один вихід та не містить елементів. Тому вихід 0 суматора (4), який відповідає кількості одиниць q=0 у комбінації з'єднаний з 0 виходом двійкового дешифратора. q В групу рівноважних комбінацій з кількістю одиниць q=1 входить Cn  C1  4 комбінацій: 4 0001, 0010. 0100, 1000. Такій групі рівноважних комбінацій відповідає РД (1), який дешифрує ці q чотири рівноважні комбінації. Він містить (n+1)=5 входів і Cn  C1  4 виходи. 4 Аналогічно з попередніми випадками, в групу рівноважних комбінацій з q=2 входить C 2  C 2  6 комбінацій: 0011, 0101, 0110, 1001, 1010, 1100. Цій групі рівноважних комбінацій 4 4 відповідає РД (2), який дешифрує ці шість рівноважних комбінацій. Цей РД (2) містить n+1=5 50 55 q входів і Cn  C 2  6 виходів. 4 Групі рівноважних комбінацій з кількістю одиниць q=3, в яку входять комбінації 0111, 1011, 1101, 1110, відповідає РД (3), який дешифрує тільки ці комбінації. Він має n+1=5 входів і q Cn  C3  4 виходи. 4 В групу рівноважних комбінацій з кількістю одиниць q=n=4 входить лише одна комбінація. Тому цій групі не відповідає РД, оскільки, аналогічно як для випадку з g=0, такий РД був би виродженим і не містив би елементів. Тому вихід n=4 суматора (4), який відповідає кількості одиниць q=n=4 у комбінації з'єднаний з 15 виходом двійкового дешифратора. 2 UA 105630 U 5 10 15 20 25 30 35 40 45 Як СВП використані широко відомі схеми, які видають сигнал помилки на своєму виході, при наявності на своїх входах більше ніж однієї одиниці або при відсутності одиниць. Така схема, наприклад, представлена в (Согомонян Е.С., Слабаков Н.В. Самопроверяемые устройства и отказоустойчивые системы. Москва: "Радио и связь", 1989, с. 113, рис. 3.23). Як елементи АБО та схем нерівнозначності використані стандартні елементи АБО та схеми нерівнозначності, інвертор побудований на основі елемента 1-НЕ. Пристрій працює наступним чином. Спочатку на вхід пристрою надходить n-розрядна комбінація двійкового коду з максимальною кількістю одиниць к в комбінації. Сигнали з входу пристрою надходять на входи 1, 2, 3, 4 суматора (4). Суматор (4) підраховує кількість одиниць на вході пристрою, та в залежності від кількості одиниць видає на одному з своїх n+1 виходів одиничний сигнал. У випадку, коли кількість одиниць у вхідній комбінації не рівна 0 і 4. Цей одиничний сигнал надходить на вхід 5 одного з n-1 РД і дозволяє його роботу. На входи 1, 2, 3, 4 схеми РД (1, 2 або 3), роботу якого було дозволено, надходять сигнали з 1, 2, 3, 4 входів завадостійкого двійкового дешифратора. Оскільки всі комбінації n-розрядного коду з кількістю одиниць q є комбінаціями одного рівноважного коду, то відповідний РД, призначений для дешифрації комбінацій цього коду, може однозначно дешифрувати такі комбінації. В результаті однозначної q дешифрації, лише на одному з C n виходів цього блока з'являється одиничний сигнал, який надходить на один з виходів завадостійкого n-входового двійкового дешифратора і призводить до дешифрації вхідної комбінації. У випадку, коли на вхід завадостійкого двійкового дешифратора подається комбінація з кількістю одиниць q, що дорівнює нулю або n=4, це призводить до появи одиничного сигналу відповідно на 0 або n=4 виході суматора (4). Одиничний сигнал з відповідного виходу суматора (4) безпосередньо надходить на вихід завадостійкого двійкового дешифратора, який відповідає поданій вхідній комбінації. Оскільки на всі інші РД, окрім задіяного, не подаються одиничні дозволяючі сигнали, то ці дешифратори не будуть задіяні, а на всіх виходах цих дешифраторів будуть нулі, і одиничні сигнали з виходів цих блоків не будуть подаватись на виходи завадостійкого двійкового дешифратора. Таким чином, лише на одному виході пристрою буде одиничний сигнал, який буде однозначно відповідати вхідній двійковій комбінації. Завадостійкий дешифратор двійкового коду також може виявляти частину помилок при своїй роботі. Важливою його перевагою є те, що вій може визначити частину пристрою, яка зробила помилку. СВП (11) призначена до виявлення помилок на виході суматора (4). При нормальній роботі суматора (4) в залежності від кількості одиниць у вхідній комбінації на одному з його виходів завжди буде одиниця. СВП (11), входи якої з'єднані з виходами суматора (4), видає сигнал помилки на своєму виході при відсутності одиниць на виходах суматора (4) чи наявності двох або більше одиниць. Тобто СВП (11) може виявляти всі помилки суматора (4), окрім перестановок одиниць на виходах суматора (4). СВП (8, 9, 10) призначені до виявлення помилок на виходах, відповідних РД (1, 2. 3). При нормальній роботі РД при надходженні вхідної комбінації в залежності від кількості одиниць, на одному з виходів суматора (4) з'явиться одиничний сигнал, який дозволить роботу одного з РД. Оскільки групам вхідних комбінацій з q=0, n не відповідають РД, то і помилок при роботі РД для цих комбінацій не буде. Тому інформація з виходів завадостійкого двійкового дешифратора, які відповідають цим комбінаціям не контролюється. Розглянемо роботу СВП (8). В таблиці наведені приклади комбінацій на її входах, при яких вона дасть чи не дасть сигнал помилки. 3 UA 105630 U Таблиця Робота схеми виявлення помилок (СВП) (8) Комбінація на вході схеми виявлення помилок (СВП) (8) Сигнал на виході Сигнал на Комбінація на виході рівноважного дешифратора Сигнал на схеми виявлення виході 1 (РД) (і) помилок (СВП) виході суматора (4) (8) інвертора (5) 1 2 3 4 0 0 0 0 0 1 0 0 1 0 1 1 помилка 0 0 1 1 1 1 помилка 0 0 1 1 1 1 помилка 0 1 1 1 1 1 помилка 1 0 0 0 0 0 помилка 1 0 0 0 1 0 1 0 0 1 1 0 помилка 1 0 0 1 1 0 помилка 1 1 0 1 1 0 помилка 5 10 15 20 25 30 35 40 Якщо була дозволена робота РД (1), то в результаті дешифрації на одному з його виходів з'явиться одиничний сигнал, а на всіх інших його виходах будуть нулі. Одиничний сигнал з виходу 1 суматора (4), який дозволив роботу цього РД (1) також надходить на вхід інвертора (5), що спричиняє появу нуля на виході цього інвертора (5). Одиничний сигнал з одного з виходів РД (1) надходить на один з входів СВП (8). На всі інші входи цієї схеми надходять нулі з інших виходів РД (1) та нуль з виходу інвертора (5). Оскільки на вході цієї СВП (8) буде лише одна одиниця, то схема не дасть сигналу помилки на своєму виході, що буде свідчити про правильну роботу РД (1). Такий випадок, продемонстрований в сьомому рядку таблиці. Якщо робота блока (1) не буде дозволена, то на його виходах будуть нулі. Нульовий сигнал з виходу 1 суматора (4), який не дозволив роботу цього РД (1),. також буде надходити на вхід інвертора (5), що призведе до появи одиниці на його виході. Нулі з виходів РД (1) та одиниця з виходу інвертору (5) буде надходити на входи СВП (8). Оскільки на входи цієї схеми (8) прийде одна одиниця, то схема (8) не дасть сигналу помилки, що буде свідчити про правильну роботу РД (1). Такий випадок, продемонстрований в першому рядку таблиці. Якщо в результаті помилки на виході РД (1), роботу якого не було дозволено з'явиться один або декілька одиничних сигналів, то на входи відповідної йому СВП (8) надійде один або декілька одиничних сигналів з виходу РД (1) та одиничний з виходу інвертора (5). Оскільки на вхід СВП (8) надійде два або більше одиничних сигналів, то на виході СВП (8) з'явиться сигнал, який буде свідчити про помилку у РД (1). Такий випадок, продемонстрований у рядках з 2 по 5 таблиці 1. Якщо в результаті помилки на виході РД (1), роботу якого було дозволено, зникне одиничний сигнал, тобто на всіх його виходах будуть нулі, то на входи відповідної цьому блоку СВП (8) надійдуть нулі з виходів РД (1) та нуль з виходу інвертора (5). Оскільки на входах цієї СВП (8) будуть тільки нулі, тобто не буде однієї одиниці, то ця схема на своєму виході дасть сигнал, який буде свідчити про наявність помилки у РД (1). Такий випадок, продемонстрований у шостому рядку таблиці 1. Якщо на виходах РД (1), роботу якого було дозволено, у результаті помилки з'являться два або більше одиничних сигнали, то на входи відповідної цьому блоку СВП (8) надійдуть дві або більше одиниць з виходів РД (1) та нуль з виходу інвертору (5). Оскільки на входах цієї СВП будуть дві або більше одиниць, то ця схема на своєму виході дасть сигнал, який буде свідчити про наявність помилки у РД (1). Такий випадок, продемонстрований у рядках з 8 по 10 таблиці 1. Якщо в результаті помилки, на одному з виходів РД (1), роботу якого було дозволено, зникне достовірний одиничний сигнал і з'явиться помилковий одиничний сигнал, на іншому його виході, то на вхід відповідної СВП (8) надійде одна одиниця з виходів РД (1) і нуль з виходу інвертора (5). Оскільки на вхід СВП (8) надійде тільки одна одиниця, то ця схема не дасть сигналу помилки на своєму виході і помилка, у цьому випадку, не буде виявлена. Вхідна комбінація СВП (8), отримана в результаті такої помилки, ідентична правильній вхідній комбінації СВП (8) для іншої вхідної комбінації завадостійкого двійкового дешифратора. Тому такий випадок також може бути продемонстрований в сьомому рядку таблиці 1. 4 UA 105630 U 5 10 15 20 25 30 35 40 45 50 55 60 Аналогічним чином виявляють помилки СВП (9) і СВП (10). Також пристрій здатен виявляти помилки при роботі схеми виявлення помилок РД (1, 2, 3), за допомогою паралельної роботи елемента АБО із схемою нерівнозначності та СВП, що під'єднані до виходів цих РД. Виявлення помилок в РД (1) за допомогою елемента АБО (12) та схеми нерівнозначності (15) працює наступним чином. Якщо була дозволена робота РД (1), тο в результаті дешифрації на одному з його виходів з'явиться одиничний сигнал, а на всіх інших його виходах будуть нулі. Одиничний сигнал з одного з виходів РД (1) надходить на один з входів схеми АБО (12). На всі інші входи цієї схеми надходять нулі з інших виходів РД (1). Оскільки на вході елемента АБО (12) надійшла одиниця, то на її виході з'явиться одиниця, яка надійде на перший вхід схеми нерівнозначності (15). Одиничний сигнал з виходу 1 суматора (4), який дозволив роботу цього РД (1), надходить на другий вхід схеми нерівнозначності (15). Оскільки на вході схеми нерівнозначності буде дві одиниці, то схема нерівнозначності (15) не дасть сигналу помилки на своєму виході, що буде свідчити про правильну роботу РД (1). Якщо робота РД (1) не буде дозволена, то на його виходах будуть нулі, які надійдуть на входи елемента АБО (12). Оскільки на входи елемента АБО (12) не надійде жодної одиниці, то на її виході буде нуль, який надійде на перший вхід схеми нерівнозначності (15). Нульовий сигнал з виходу 1 суматора (4). який не дозволив роботу цього РД (1), буде надходити на другий вхід схеми нерівнозначності (15). Оскільки на входи схеми нерівнозначності (15) прийдуть два нулі, то схема нерівнозначності (15) не дасть сигналу помилки, що буде свідчити про правильну роботу РД (1). Якщо в результаті помилки на виході РД (1), роботу якого не було дозволено з'явиться один або декілька одиничних сигналів, то на входи відповідної йому елемента АБО (12) надійде один або декілька одиничних сигналів з виходу РД (1). Оскільки на вхід елемента АБО (12) надійде два або більше одиничних сигналів, то на її виході з'явиться одиничний сигнал, який надійде на перший вхід схеми нерівнозначності (15). Нульовий сигнал з виходу 1 суматора (4), який не дозволив роботу цього РД (1), буде надходити на другий вхід схеми нерівнозначності (15). Оскільки на входи схеми нерівнозначності (15) прийде один нуль і одна одиниця, то схема нерівнозначності (15) дасть сигнал помилки, що буде свідчити про помилку при роботі РД (1). Якщо в результаті помилки на виході РД (1), роботу якого було дозволено, зникне одиничний сигнал, тобто на всіх його виходах будуть нулі, то на входи відповідного цьому блоку елемента АБО (12) надійдуть нулі з виходів РД (1), що призведе до появи нуля на виході елемента АБО (12). Цей нуль надійде на перший вхід схеми нерівнозначності (15). Одиничний сигнал з виходу 1 суматора (4), який дозволив роботу РД (1) також надходить на другий вхід схеми нерівнозначності (15). Оскільки на входи схеми нерівнозначності (15) прийде один нуль і одна одиниця, то схема нерівнозначності (15) дасть сигнал помилки, що буде свідчити про помилку при роботі РД (1). Якщо в результаті помилки, на одному з виходів РД (1), роботу якого було дозволено, з'явиться один або більше помилкових одиничних сигналів (при цьому достовірний одиничний сигнал може залишитися, а може теж зникнути в результаті помилки), то на вхід елемента АБО (12) надійдуть одна або більше одиниць, що призведе до появи одиниці на її виході. Ця одиниця надійде на перший вхід схеми нерівнозначності (15). Одиничний сигнал з виходу 1 суматора (4), який дозволив роботу РД (1), надійде на другий вхід схеми нерівнозначності (15). Оскільки на входи схеми нерівнозначності (15) прийде дві одиниці, то схема нерівнозначності (15) не дасть сигналу помилки, і помилка не буде виявлена. Схеми виявлення помилок, що складаються із схеми АБО 13, 14 та схем нерівнозначності 16, 17, які відповідають РД (2, 3), працюють аналогічно. Схеми, що складаються з елемента АБО та схеми нерівнозначності, виявляють менше помилок при роботі відповідного їм РД, ніж схеми СВП, які відповідають цим РД. Але апаратурні затрати на реалізацію схем, що складаються з елемента АБО та схеми нерівнозначності, менші, ніж на реалізацію відповідної СВП. Паралельна робота схем, що складаються з елемента АБО та схеми нерівнозначності, і СВП призводить до можливості виявляти помилки при роботі схем виявлення помилок. Оскільки схема, що складається з схеми АБО (12) і схеми нерівнозначності (15), виявляє менше помилок, ніж СВП (8), то наявність сигналу помилки на виході СВП (8) і відсутність сигналу помилки на виході схеми нерівнозначності (15) не обов'язково буде свідчити про помилку в роботі схем виявлення помилок РД (1), бо може свідчити про наявність помилки в РД (1), яку може виявити СВП (8) і не може виявити схема, що складається зі схеми АБО (12) і 5 UA 105630 U 5 схеми нерівнозначності (15). Але, якщо СВП (8) не дасть сигналу помилки, а на виході схеми нерівнозначності (15) з'явиться сигнал помилки, то це однозначно буде свідчити про помилку в роботі схем виявлення помилок РД (1). Аналогічно можна виявити помилки при роботі схем виявлення помилок РД (2,3). Внесені зміни дозволяють підвищити завадостійкість пристрою при дешифрації двійкових комбінацій, розширюючи функціональні можливості самого дешифратора. ФОРМУЛА КОРИСНОЇ МОДЕЛІ 10 15 20 Завадостійкий n-входовий двійковий дешифратор, що містить суматор, не більше n  1 схем q рівноважних дешифраторів (далі РД) з n  1 входами і C n (q  [1, ..., n  1]) виходами, де n кількість входів завадостійкого двійкового дешифратора, q - можлива кількість одиниць у вхідній комбінації, елементи АБО та схеми нерівнозначності, перші n-входи кожного РД і всі nвходи суматора з'єднані з n-входами завадостійкого дешифратора, а (n  1) -й вхід РД - з відповідним виходом суматора, входи кожного елемента АБО зв'язані з виходами відповідного РД, а виходи з'єднані з першими входами відповідних схеми нерівнозначності, другий вхід яких зв'язаний з відповідним виходом суматора, який відрізняється тим, що в завадостійкий nвходовий двійковий дешифратор додатково введені n  1 схем виявлення всіх помилок (СВП), входи кожної із яких з'єднані з виходами відповідних РД і виходами відповідних додатково введених інверторів, а виходи є виходами завадостійкого дешифратора, при цьому вхід кожного інвертора з'єднаний з виходом суматора, відповідним цьому РД, і кожна СВП має на один більше входів, ніж відповідний їй РД, і один вихід, окрім цього додатково введена СВП для суматора, n  1 входів якої з'єднуються з n  1 виходами суматора, а вихід є виходом завадостійкого дешифратора. 6 UA 105630 U Комп’ютерна верстка Л. Ціхановська Державна служба інтелектуальної власності України, вул. Василя Липківського, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут інтелектуальної власності”, вул. Глазунова, 1, м. Київ – 42, 01601 7