Модифікована лінза френеля

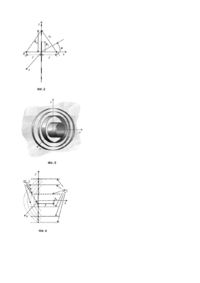
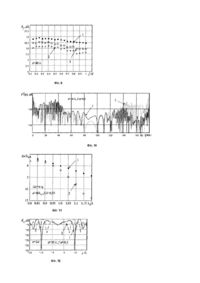
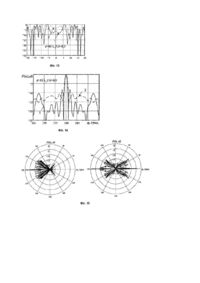
Корисна модель відноситься до антеної техніки. Може бути використана в техніці наземного й космічного радіозв'язку, радіолокації для створення гостроспрямованого випромінювання, формування квазіплоских полів у коліматорах і збіжних хвильових фронтів у фокусуючи х пристроях НВЧ, з метою підвищення коефіцієнта спрямованої дії (КСД) й поліпшення фокусування, зниження рівня випромінювань у напрямку протилежному головній пелюстці діаграми спрямованості. Більшість антен, що працюють у діапазонах сантиметрових і більш коротких хвиль, відносяться до класу апертурних антен оптичного типу. До таких антен можна віднести, наприклад, добре відомі з оптики [1] лінзи Френеля, в яких поверхня, що переломлює, являє собою плоску одношарову провідну дискретну поверхню [2, 3]. Дискретні поверхні можуть використовуватися не тільки як антенні елементи, але й у коліматорах для створення квазіплоских або сфокусованих полів [4, 5]. Лінзи Френзеля (прототип), наприклад, застосовуються в міліметровому й сантиметровому діапазонах хвиль як пасивні ретранслятори й кільцеві антенні директори [6]. Однак ці антенні елементи мають властивий основний недолік, який обмежує можливості практичного застосування - це багатофокусність. Наприклад, у тому випадку, коли класична симетрична лінза Френеля опромінюється точковим джерелом електромагнітного поля, розсіяне поле формує не одну, а дві головні пелюстки діаграми спрямованості (ДС) у прямому й зворотному напрямку, а також фокусується на поздовжній осі в області фокальних точок, які можна назвати областями вторинного фокусування або «паразитними» фокусами. Наявність ефекту багато фокусності є однією з основних причин зниження коефіцієнта спрямованої дії (КСД) антени, погіршення захисних властивостей антени в напрямку протилежному напрямку головної пелюстки ДС. Фокусування розсіяного поля в місці розміщення опромінювача погіршує коефіцієнт біжучої хвилі (КБХ) у живильному тракті. Ідея створення антенних елементів у вигляді лінзи Френеля базується на принципі Гюйгенса-Френеля й понятті зон Френеля. Лінза Френеля формується шляхом розбивки утворюючої плоскої поверхні S на зони Френеля [1, 2, 3] з наступним заповненням парних (з номерами які дорівнюють 2n, де n=1,2,...N, N - є загальне число зон у розкриві, парне заповнення), або непарних (з номерами які дорівнюють 2n-1, де n=1,2,...N, N - є загальне число зон у розкриві, непарне заповнення) зон тонким шаром добре провідного матеріалу (фіг.1). Така лінза являє собою провідну дискретно-плоску поверхню з парним або непарним заповненням, відповідно. При осьовому опроміненні такої дискретної поверхні плоскою хвилею, наприклад, що приходить із позитивного напрямку осі z, розсіяне поле фокусується не тільки у двох ближніх фокальних точках F1 й F2, але також й у нескінченно віддалених точках (х=±¥) на оптичній осі (фіг.2). Аналогічно цьому, при опромінюванні її джерелом сферичної хвилі, що, наприклад, знаходиться на оптичній осі в точці х=f, розсіяне поле також фокусується не тільки в нескінченно віддалених точках (х=±¥) на оптичній осі, але також й у дво х ближніх фокальних точках F1 й F2 . Отже, при практичній реалізації плоских лінз Френеля як елементів антенних або фокусуючи х пристроїв (наприклад, як пасивних ретрансляторів або кільцевих антенних директорів [6]) проявляється властивий їм недолік: більш ніж половина енергії падаючого поля використовується не за призначенням, що, зокрема, є причиною зниження коефіцієнта спрямованої дії D й коефіцієнта захисної дії таких антенних пристроїв. Нагадаємо, що принцип розбивання плоскої поверхні, на зони Френеля забезпечується виконанням умови: rn = f + n l / 2 , де: n - номер зони, rn - відстань від джерела до зовнішнього краю n-ї зони, f - фокусна відстань, l - довжина хвилі (фіг.2). При цьому різниця фаз полів створюваних джерелом монохроматичної електромагнітної хвилі в крайніх точках кожної зони становить 180°. Радіуси зон Френеля Rn визначаються співвідношенням: Rn = y 2 + z 2 = fnl + (nl / 2)2 n n . (1) При опромінюванні такої дискретної поверхні джерелом сферичної хвилі її елементи, перебуваючи в площині розкриву лінзи, «затінюють» області протифазних полів у розкриві, тобто в них утворяться «тіньові» зони. Для лінзової антени Френеля поставлена задача різкого зниження рівня поля розсіяного в напрямку джерела падаючої хвилі, зниження рівня задніх бічних пелюсток діаграми спрямованості й збільшення коефіцієнта спрямованої дії, зменшення впливу е фекту називаного «реакцією дзеркала на опромінювач». Принцип дії пропонованої конструкції лінзи Френеля, названої модифікованою лінзою Френеля (МЛФ), подібний до принципу дії канонічної лінзи Френеля, а саме, як і у прототипу, уявлювана плоска поверхня розкриву лінзи також дискретизується (розбивається на зони Френеля). Технічним рішенням поставленого завдання є те, що в конструкції модифікованої лінзи Френеля, передбачається інший спосіб усунення протифазних зон, тобто їх «затінення». А саме: елементи МЛФ «затінюють» парну підмножину зон Френеля на плоскій поверхні розкриву, при цьому самі вони знаходяться поза тіньовими зонами на згаданій поверхні, тобто не лежать у площині розкриву й, наприклад, орієнтовані ортогонально стосовно неї (фіг.2). У такому випадку елементи МЛФ являють собою перетин сімейства утворюючих, поверхонь у вигляді поверхонь кругових циліндрів Рk, які, ортогональні до площини розкриву лінзи. Ціль такої модифікації класичної лінзи Френеля полягає в тому, щоб, по-перше, - знизити рівень відбиттів від лінзи убік джерела падаючої хвилі, а по-друге, - частково перенаправити енергію відбитих полів у прямому напрямку. Геометрія МЛФ формується у такий спосіб. Спочатку проводиться дискретизація (поділ) площини розкриву (площини х=0) майбутньої лінзи на зони Френеля. Межа n-ї зони Френеля являє собою лінію перетинання цієї площини з n-ю січною поверхнею - елементом конформного сімейства у вигляді поверхонь співфокусних параболоїдів обертання {Qn,1} з фокусом у точці з координатами х=x0 ,у=0, z=0 (фіг.4). Друге сімейство {Qn,2} січни х поверхонь - це кругові конічні поверхні, які мають загальну вершину в точці з координатами х=x0 , у=0, z=0. Кожна n-а поверхня цього сімейства проходить через границю n-ї зони Френеля (фіг.5) на площині х=0. Третє сімейство {Рk} поверхонь, що будемо називати утворюючими поверхнями, це поверхні співвісних кругових циліндрів, осі яких збігаються з віссю х. Кожна одна утворююча поверхня проходить через верхню границю однієї з непарних зон Френеля. Два сусідніх елементи Q2n-1,2 й Q2n,2 із сукупності {Qn,2} обмежують («відтинають») на утворюючій поверхні Р2n1 й область, ширина якої l 2n-1 визначається співвідношенням l2n -1 = (r 2n - r 2n -1 ) / tgy 2n , n = 1 N . (2) ,..., Багатозв'язна незамкнена поверхня S , що утворена з таких циліндричних відрізків, і розглядається як модифікована дискретна поверхня Френеля (її профіль, - перетин площиною х=0, показаний на фіг.6). Якщо елементи цієї поверхні виконати із провідного матеріалу, то в результаті одержимо конструкцію модифікованої лінзи Френеля. На цьому ж рисунку для наочності показано як у МЛФ усуваються протифазність полів у розкриву лінзи й у парних зонах Френеля утворяться «тіньові» області. Для обгрунтування запропонованого конструктивного розв'язання було проведено чисельний експеримент, заснований на розв'язанні електродинамічного завдання про знаходження поля, розсіяного модифікованою лінзою Френеля, при опромінюванні джерелом електромагнітного поля. З цією метою виконувалося коректне розв'язання відповідної двовимірної (геометрія лінзи й характеристики електромагнітного поля не залежать від координати z) задачі дифракції. У формуванні двовимірної модифікованої поверхні S беруть участь три сімейства поверхонь. Перше сімейство {Qn,1} - січні поверхні: параболічні циліндри з фокусом на лінії х = 0, у=0, др уге сімейство {Qn,2} - січні х поверхні: напівплощини, які починаються на лінії х=х0, у=0, третє сімейство Р2n-1 - утворюючі поверхні: сукупність площин паралельних до площини у=0. Нехай на основі дискретної модифікованої поверхні S, геометрія якої визначена в результаті процедури дискретизації за описаним вище алгоритмом і формулами (1), (2), утворена МЛФ із розміром розкриву d й фокусною відстанню f. Оскільки розглянута дифракційна задача є двовимірною, то граничні умови, амплітудно-фазові розподіли полів джерел не залежать від вибраної координати (у цьому випадку, від координати z). Потрібно знайти розподіл розсіяного поля в далекій зоні, розрахува ти діаграму спрямованості й коефіцієнт спрямованої дії (КСД) модифікованої лінзи Френеля. Потім, порівнюючи одержані результати з аналогічними розрахунками, виконаними для моделі канонічної лінзи Френеля, оцінити переваги у спрямованих й фокусуючи х властивостя х, виграш у КСД, які досягаються модифікованою лінзою Френеля. 0 0 Отже, розглянемо задачу ди фракції Е - поляризованого монохроматичного електромагнітного поля E , H на модифікованій дискретній поверхні S (незамкненому багато-зв'язному ідеально провідному двосторонньому екрані), розміщеній в безмежному однорідному ізотропному середовищі з параметрами e 0 ,m 0 . Поставлена задача зводиться до знаходження розподілу густини поверхневого струму на екрані за допомогою чисельного розв'язання інтегрального рівняння Фредгольма першого роду: wma jx (g )K( t, g)dg = E0 ( t) x 4 ò L (3) шляхом зведення його до системи лінійних алгебраїчних рівнянь методом колокації [8]. Контур L має вигляд перетину дискретної поверхні S площиною z=0 й при чисельному розв'язанні рівняння (3) методом колокації на ділянку контуру L розміром у довжину хвилі припадало приблизно 30...40 точок колокації. Знайдене в результаті такого розв'язання розподілення густини поверхневого струму j = z0 j z на поверхні S дає можливість шляхом використання коректних методів чисельного інтегрування розрахувати вторинні (розсіяні поля, а також інші необхідні характеристики. Для того щоб можна було порівнювати характеристики двох типів лінз, паралельно проводилося розв'язання аналогічної задачі для канонічної лінзи Френеля (ЛФ). У такій постановці результати розв'язання даної задачі дозволяють коректно оцінити характеристики розглянути х лінзових антен. Процедура розв'язання задачі складається із двох послідовно виконуваних етапів. Перший етап, - коли 0 0 джерелом первинного (падаючого) монохроматичного поля E = z 0 Ez , є плоска хвиля (при цьому розраховується характеристика розсіювання, визначаються фокусуючі властивості й уточнюється положення фокальної лінії), другий, - коли джерелом служить нитка електричного струму, яка розміщена на фокальній лінії (при цьому розраховуються амплітудно-фазові розподіли поля в розкриві й визначаються спрямовані властивості). Обговорення одержаних результатів. Результати розрахунків й аналіз характеристик модифікованих лінз Френеля, які наведені нижче, виконувалися для декількох варіантів МЛФ із розмірами розкриву d=40 l й d=50 l . Криві, наведені на фіг.7, 8 відображають розподіл амплітуди сумарного поля у фокальній області лінз двох типів при опромінюванні їх плоскою хвилею, що поширюється в напрямку позитивних значень координати х. Тут порівняння властивостей цих лінз Френеля показує, що менший розмір фокальної плями на горизонтальній осі (фіг.7) має МЛФ, а положення фокуса цієї лінзи практично збігається із заданими початкове. При цьому для канонічної ЛФ, положення максимуму амплітудного розподілу зміщено щодо геометричного фокуса на величину Dx =0,6 l . Як показують графіки, зображені на фіг.8 амплітудні розподіли полів у фокальній площині поблизу поздовжньої осі МЛФ і ЛФ мало відрізняються. Для того щоб наочніше продемонструвати відмінності фокусуючи х властивостей двох типів лінз уведемо показник, який можна назвати коефіцієнтом фокусування kf, обумовлений наступним виразом: 2 é ù Es ( x 0 ,0) ê z ú k f = 20lgê d ú 2 ê d / 2 E s (x 0 , y) dy ú ò-d / 2 z ë û. Як показали розрахунки здатність концентрувати поле в області фокальної лінії в МЛФ і ЛФ різна. Так на фіг.9 наведено дані про значення коефіцієнта фокусування kf, для лінз із розміром розкриву 40l при різних значеннях відношення f/d. Видно, що для розглянутих лінз залежність kf від фокусної відстані відносно мала. Проте, найкращі фокусуючі властивості спостерігаються поблизу значень f/d=0,4, при цьому, що особливо треба відзначити, коефіцієнт фокусування для МЛФ приблизно на 2...2,5 дБ більше, ніж для ЛФ із парним заповненням, і приблизно на 4...5 дБ більше, ніж для ЛФ із непарним заповненням. Про переваги МЛФ порівняно з канонічною ЛФ найбільше яскраво свідчать результати розрахунків діаграм розсіювання для випадку падіння плоскої хвилі, які наведено на фіг.10. Ці криві нормовані до того самого максимального значення амплітуди розсіяного поля. Тут для МЛФ спостерігається різке (на 10...30 дБ) зниження рівня розсіяного поля в секторі кутів 140°£j£220°, тобто в напрямках зворотних щодо напрямку падіння плоскої хвилі. Оскільки геометрія лінз на основі розглянутих дискретних поверхонь й, зокрема, МЛФ заснована на дискретизації плоскої поверхні розкриву на зони Френеля, розміри яких тісно пов'язані з довжиною хвилі, то особливий інтерес становить аналіз властивостей таких поверхонь залежно від довжини хвилі. У цьому зв'язку, наприклад, показові графіки, подані на фіг.10, де показано як зміщується реальна фокальна лінія щодо свого положення заданого спочатку в процесі дискретизації на розрахунковій довжині хвилі l0 , тобто частотні властивості. Можна відзначити, що у двох випадках, поданих на цьому рисунку, зі зменшенням довжини хвилі відбувається зсув фокальної лінії в напрямку від лінзи. Однак видно, що для модифікованої лінзи характерне менше й більш плавне зростання величини зміщення Dx порівняно з ЛФ. Другий етап розрахунків (коли опромінювач у вигляді нитки електричного струму знаходиться на реальній фокальній лінії) містив у собі розрахунки амплітудно-фазового розподілення (АФР) сумарного поля в площині паралельній розкриву лінз на відстані 2d від нього, результати яких відображені у вигляді графіків на фіг.12, 13. Криві, які тут наводяться, дозволяють оцінити можливості використання МЛФ коліматори для створення плоского поля в ближній зоні. Порівнюючи області, у яких флуктуації амплітуди сформованого поля перебувають у межах ±2 дБ, а флуктуації фази - у межах ±30 градусів не важко бачити, що у випадку МЛФ ця область приблизно на 30% ширше, ніж для ЛФ. Спрямовані властивості МЛФ порівняно з ЛФ ілюструють діаграми спрямованості, наведені на фіг.14 і фіг.15. При розрахунку діаграм спрямованості покладалося, що діаграма спрямованості f(j) опромінювана секторна: f (j) = 1, j Î [ -y 0 , y 0 ] ü ý f (j) = 0, j Ï [ - y 0 , y 0 ]þ де ці y 0 - половина кута розкриву лінзи. Аналізуючи ДН в області кутів поблизу головної пелюстки (фіг.14) можна відзначити, що характер зміни ближніх бічних пелюсток для обох типів лінз відрізняється. Так, якщо ДН МЛФ має явно виражений пелюстковий характер. Відмінності в ширині найголовнішої пелюстки на цих рисунках малопомітні, однак, як показують детальні розрахунки, ця величина, визначена на рівні - 3 дБ, становить 1,0° для МЛФ і 1,2° для ЛФ, тобто головна пелюстка ДН ЛФ на 20% ширше, ніж головний пелюсток діаграми МЛФ. Набагато помітніше проявляються відмінності діаграм спрямованості в області заднього півпростору (фіг.15). Добре видно, що рівень заднього й далеких бічних пелюсток ДН у МЛФ на 15...20 дБ нижче, ніж у ЛФ. Можна припускати, що рівень розсіяного поля в напрямку джерела в області фокуса також знижується, що сприяє підвищенню КБХ у тракті, який вживлює опромінювач реальної модифікованої лінзової антени Френеля. Проведені розрахунки дають підставу стверджувати, що запропонована конструкція МЛФ забезпечує розсіювання поля переважно в одному (прямому) напрямку й цим істотно відрізняється від канонічної ЛФ. Внаслідок цього спрямовані властивості модифікованої лінзи краще ніж у класичної лінзи Френеля, про що свідчать результати розрахунків коефіцієнта спрямованої дії, наведені нижче. Аналіз частотних властивостей модифікованої лінзи Френеля з розміром розкриву d=40l0 проводився при зміні довжини хвилі в межах 0,8£l0/l£1,5. При такій зміні, зокрема, має місце ефект зсуву положення фокальної лінії щодо початкового («геометричного») фокуса лінзи. Досліджуючи частотні властивості МЛФ можна «відстежити» цей зсув за кожної зміни довжини хвилі, і при розрахунках КСД поміщати джерело падаючого поля на лінію «реального» фокуса. У цьому випадку результати відображають частотні властивості самої дискретної модифікованої поверхні Френеля (фіг.16). Тут порівнюючи результати, одержані для двох типів дискретних поверхонь, відзначимо, що КСД лінзи, утвореної модифікованою поверхнею помітно (на 1,5...2,4 дБ) перевищує КСД класичної ЛФ. Причому, максимальне значення КСД, яке дорівнює 16,4 дБ, досягається на частоті, приблизно дорівнює 1,1f0, де f0 тастота, що відповідає ви хідній розрахунковій довжині хвилі l0. Проаналізувати залежності КСД від фокусної відстані у випадку, коли джерело падаючого поля перебуває в «реальному» фокусі, дають можливість результати розрахунків (фіг.17), виконаних для лінз розмір розкриву яких становить 40l. Видно, що зі зростанням відношення f/d, починаючи від f/d=0,2 і до f/d=0,65, коефіцієнт спрямованої дії МЛФ монотонно зростає із 15,8 дБ до 17,6 дБ і далі майже не змінюється. У той самий час КСД лінзи Френеля з парним заповненням зон змінюється набагато повільніше зростаючи з 14,7 дБ при f/d=0,2 до 15,3 дБ при f/d=1. КСД у МЛФ за всі х значень f/d більше ніж у ЛФ, причому максимальний виграш по КСД лінзи з модифікованою поверхнею Френеля порівняно з канонічним варіантом ЛФ має місце при f/d=0,65 й досягає 2,6 дБ. Висновок: результати проведених розрахунків на моделях модифікованих лінз Френеля й порівняння одержаних результатів з характеристиками канонічної моделі лінзи Френеля показали таке: - МЛФ забезпечують більш вузьку головну пелюстку ДН і більш низький рівень далеких бічних пелюстків ДН ; - МЛФ мають виграш у КСД, який досягає 2,4 дБ; - відносний рівень поля розсіяного МЛФ у напрямку джерела падаючого поля на 10...30 дБ менше; - значення коефіцієнта фокусування для МЛФ більше на 2...2,5 дБ ніж для ЛФ із парним заповненням, і приблизно на 4...5 дБ більше, ніж для ЛФ із непарним заповненням. На основі розв'язання поставленої дифракційної задачі й наведених вище результатів можна досить коректно, обґрунтовано й достовірно зробити висновок, що модифіковані лінзи Френеля помітно перевершують класичні лінзи Френеля за своїми спрямованими і фокусуючими властивостями. Перелік фігур креслення Фіг.1. Геометрія зон дискретно-плоскої поверхні Френеля Фіг.2. Профіль дискретно-плоскої поверхні Френеля Фіг.3. Зовнішній вигляд модифікованої лінзи Френзеля Фіг.4; Фіг.5; Фіг.6. Формування геометрії модифікованої лінзи Френзеля Фіг.7. Розподіл амплітуди поля на поздовжній осі Фіг.8. Розподіл амплітуди у фокальній у фокальній площині, 1 - МЛФ, 2 - ЛФ Фіг.9. Залежність kf від фокусної відстані: 1 - МЛФ, 2 - ЛФ (при непарному заповненні), 3 - ЛФ (при парному заповненні) Фіг.10. Діаграми розсіяного поля: 1 - МЛФ, 2 - ЛФ (при парному заповненні). Фіг.11. Залежність положення фокуса від довжини хвилі: 1 - МЛФ, 2 - ЛФ. Фіг.12; Фіг.13. Амплітудно-фазові розподіли полів у розкриві: 1 - МЛФ, 2 - ЛФ. Фіг.14. Діаграми спрямованості: 1 - МЛФ, 2 - ЛФ. Фіг.15. Діаграми спрямованості: d=50l, f/d=0,5, a - МЛФ, б - ЛФ. Фіг.16. Частотні залежності КСД: 1 (МЛФ, 2 (ЛФ (при парному заповненні. Фіг.17. Залежність КСД від фокусної відстані: 1 - МЛФ, 2 - ЛФ (при парному заповненні). Джерела інформації: 1. Кольер Р., Беркхарт К., Лин Л. Оптическая топография. 1973 - М: Мир. - 354 с. 2. L. Van Buskirk, C.E. Hendrix. The Zone Plate as a Radio Frequency Focusing Element. // IRE 3. Цалиев Т.А. Электродинамические свойства дискретных поверхностей // Известия вузов. Радиоэлектроника. - 2000. - 43. - № 5-10. - С.13-22. 4. Базарский О.В., Колесников А.И., Хлянич Я.Л. Частотные свойства зонированных линз Френеля. // Радиотехника и электроника. - 1980. - № 12, 5. Байбулатов Ф.Х., Минин И.В. Исследование фокусирующих свойств зонной пластинки Френеля. // Радиотехника и электроника. 1985. - № 9. 6. Айзенберг Г.З., Ямпольский В.Г. Пассивные ретрансляторы для радиорелейных линий. - 1973. - М.: Связь. - 208 с.