Спосіб визначення параметрів нелінійної дисипативної коливальної системи
Формула / Реферат
Спосіб визначення параметрів нелінійної дисипативної коливальної системи, за яким формують шість режимів коливань нелінійної дисипативної коливальної системи, в першому і другому режимах задають перше початкове і перше кінцеве, друге початкове і друге кінцеве значення амплітуди коливань відповідно, вимірюють перший і другий часові інтервали і числа циклів коливань в першому і другому часових інтервалах відповідно, перший раз змінюють інерційність нелінійної дисипативної коливальної системи і проводять вищевказану сукупність операцій по визначенню третього і четвертого часових інтервалів і чисел циклів коливань в цих часових інтервалах при зміні амплітуди коливань від першого початкового значення до першого кінцевого значення, від другого початкового значення до другого кінцевого значень відповідно, другий раз змінюють інерційність нелінійної дисипативної коливальної системи і проводять вищевказану сукупність операцій по визначенню п'ятого і шостого часових інтервалів і чисел циклів коливань в цих часових інтервалах при зміні амплітуди коливань від першого початкового значення до першого кінцевого значення, від другого початкового значення до другого кінцевого значення, який відрізняється тим, що шість режимів коливань формують як режими вимушених коливань, в кожному із шести режимів коливань фіксують значення нижніх і верхніх частот діапазонів частот, що відповідають змінам амплітуд вимушених коливань від першого початкового значення до першого кінцевого значення в першому, третьому і п'ятому режимах, від другого початкового до другого кінцевого значення в другому, четвертому і шостому режимах, причому зміну частоти сигналу вимушеної дії проводять із першою, другою, третьою, четвертою, п'ятою і шостою швидкостями для першого, другого, третього, четвертого, п'ятого, шостого режимів відповідно, а значення частот ![]() вільних коливань лінійної породжувальної системи, інерційно-жорсткісних параметрів ms, сs по S-ій нормальній координаті визначають на підставі співвідношень:
вільних коливань лінійної породжувальної системи, інерційно-жорсткісних параметрів ms, сs по S-ій нормальній координаті визначають на підставі співвідношень:
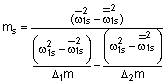 ,
,
![]()
або
![]() ,
,
![]()
або
![]() ,
,
де :
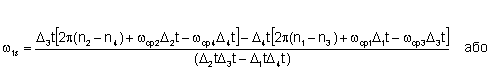
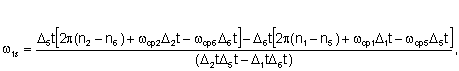
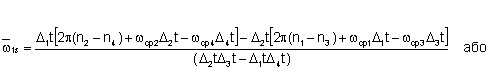
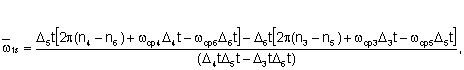
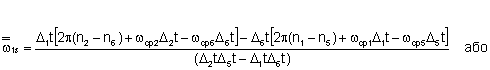
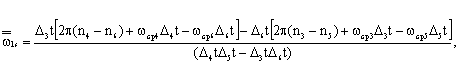
![]() ,
, ![]() ,
, ![]() ,
,
![]() - перша і друга додаткові маси відповідно;
- перша і друга додаткові маси відповідно; ![]() - число циклів вимушених коливань в часовому інтервалі
- число циклів вимушених коливань в часовому інтервалі ![]() при зміні частоти вимушених коливань із першою постійною швидкістю
при зміні частоти вимушених коливань із першою постійною швидкістю ![]() від першого початкового значення
від першого початкового значення ![]() до першого кінцевого значення
до першого кінцевого значення ![]() для маси
для маси ![]() ;
; ![]() - число циклів вимушених коливань в часовому інтервалі
- число циклів вимушених коливань в часовому інтервалі ![]() при зміні частоти вимушених коливань із другою постійною швидкістю
при зміні частоти вимушених коливань із другою постійною швидкістю ![]() від другого початкового значення
від другого початкового значення ![]() до другого кінцевого значення
до другого кінцевого значення ![]() для маси
для маси ![]() ;
; ![]() - число циклів вимушених коливань в часовому інтервалі
- число циклів вимушених коливань в часовому інтервалі ![]() при зміні частоти вимушених коливань із третьою постійною швидкістю V3 від першого початкового значення
при зміні частоти вимушених коливань із третьою постійною швидкістю V3 від першого початкового значення ![]() до першого кінцевого значення
до першого кінцевого значення ![]() для маси
для маси ![]() при першій зміні інерційності коливальної системи;
при першій зміні інерційності коливальної системи; ![]() - число циклів вимушених коливань в часовому інтервалі
- число циклів вимушених коливань в часовому інтервалі ![]() при зміні частоти вимушених коливань із четвертою постійною швидкістю
при зміні частоти вимушених коливань із четвертою постійною швидкістю ![]() від другого початкового значення
від другого початкового значення ![]() до другого кінцевого значення
до другого кінцевого значення ![]() для маси
для маси ![]() при першій зміні інерційності;
при першій зміні інерційності; ![]() - число циклів вимушених коливань в часовому інтервалі
- число циклів вимушених коливань в часовому інтервалі ![]() при зміні частоти вимушених коливань із п'ятою постійною швидкістю
при зміні частоти вимушених коливань із п'ятою постійною швидкістю ![]() від першого початкового значення
від першого початкового значення ![]() до першого кінцевого значення
до першого кінцевого значення ![]() для маси
для маси ![]() при другій зміні інерційності;
при другій зміні інерційності; ![]() - число циклів вимушених коливань в часовому інтервалі
- число циклів вимушених коливань в часовому інтервалі ![]() при зміні частоти вимушених коливань із шостою постійною швидкістю
при зміні частоти вимушених коливань із шостою постійною швидкістю ![]() від другого початкового значення
від другого початкового значення ![]() до другого кінцевого значення
до другого кінцевого значення ![]() для маси
для маси ![]() при другій зміні інерційності;
при другій зміні інерційності; ![]() - середні частоти діапазонів частот, що відповідають часовим інтервалам
- середні частоти діапазонів частот, що відповідають часовим інтервалам ![]() відповідно і визначаються співвідношеннями:
відповідно і визначаються співвідношеннями:
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ,
,
де: ![]() - верхні і нижні частоти діапазонів частот, що відповідають зміні амплітуди вимушених коливань від першого початкового значення
- верхні і нижні частоти діапазонів частот, що відповідають зміні амплітуди вимушених коливань від першого початкового значення ![]() до першого кінцевого значення
до першого кінцевого значення ![]() ;
; ![]() - верхні і нижні частоти діапазонів частот, що відповідають зміні амплітуди вимушених коливань від другого початкового значення
- верхні і нижні частоти діапазонів частот, що відповідають зміні амплітуди вимушених коливань від другого початкового значення ![]() до другого кінцевого значення
до другого кінцевого значення ![]() .
.
Текст
Спосіб визначення параметрів нелінійної дисипативної коливальної системи, за яким формують шість режимів коливань нелінійної дисипативної коливальної системи, в першому і другому режимах задають перше початкове і перше кінцеве, друге початкове і друге кінцеве значення амплітуди коливань відповідно, вимірюють перший і другий часові інтервали і числа циклів коливань в першому і другому часових інтервалах відповідно, перший раз змінюють інерційність нелінійної дисипативної коливальної системи і проводять вищевказану сукупність операцій по визначенню третього і четвертого часових інтервалів і чисел циклів коливань в цих часових інтервалах при зміні амплітуди коливань від першого початкового значення до першого кінцевого значення, від другого початкового значення до другого кінцевого значень відповідно, другий раз змінюють інерційність нелінійної дисипативної коливальної системи і проводять вищевказану сукупність операцій по визначенню п'ятого і шостого часових інтервалів і чисел циклів коливань в цих часових інтервалах при зміні амплітуди коливань від першого початкового значення до першого кінцевого значення, від другого початкового значення до другого кінцевого значення, який відрізняється тим, що шість ре 2 2 (13) U (1s 1s ) , ms 2 2 2 2 1s 1s 1s 1s 1m 2m 2 2 (1s 1s )m s (ms 1m) 1m 56369 cs або 2 (11) (2 1s )m s (m s 2m) c s 1s , 2m 2 2 cs (2 1s )(m s 1m) m 2 1s (1s 1s )1 s ms 1m 1m UA 2 0s або 2 2 c (2 1s )( m s 2m) m 2 s 1s ( 1s 1s )1 s , ms 2m 2m (19) 2 0 s де : 1s 3 t 2(n2 n4 ) cp2 2 t cp 4 4 t 4 t 2(n1 n3 ) cp11t cp3 3 t ( 2 t 3 t 1t 4 t ) або 3 1s 1s 5 t 2(n2 n6 ) cp2 2t cp6 6 t 6 t 2(n1 n5 ) cp11t cp5 5 t ( 2t 5 t 1t 6 t ) , ( 2 t 3 t 1t 4 t ) 5 t 2(n4 n6 ) cp 4 4 t cp6 6 t 6 t 2(n3 n5 ) cp3 3 t cp5 5 t ( 4 t 5 t 3 t 6 t ) 1t 2(n2 n6 ) cp2 2t cp6 6 t 6 t 2(n1 n5 ) cp11t cp5 5 t 1s 1s c sms1 h2 , s 4 1t 2(n2 n4 ) cp2 2t cp4 4 t 2 t 2(n1 n3 ) cp11t cp3 3 t 1s 1s 56369 ( 2t 5 t 1t 6 t ) або , або 3 t 2(n4 n6 ) cp 4 4 t cp6 6 t 6 t 2(n3 n5 ) cp3 3 t cp5 5 t ( 4 t 5 t 3 t 6 t ) 2 1s c s (ms 1m)1 hs , 2 , вимушених коливань із п'ятою постійною швидкістю V5 від першого початкового значення X до 1 1s c s (m s 2m) 1 h s , першого 1m, 2m(1m 2m, 1m ms, 2m ms ) - перша (ms 2m) при другій зміні інерційності; n6 - число циклів вимушених коливань в часовому інтервалі 6 t при зміні частоти вимушених коливань із і друга додаткові маси відповідно; n 1 - число циклів вимушених коливань в часовому інтервалі 1t при зміні частоти вимушених коливань із першою постійною швидкістю V1 від першого початкового значення X1 до першого кінцевого значення X2 для маси ms ; n 2 - число циклів вимушених коливань в часовому інтервалі 2 t при зміні частоти вимушених коливань із другою постійною швидкістю V2 від другого початкового значення X3 до другого кінцевого значення X 4 для маси ms ; n 3 - число циклів вимушених коливань в часовому інтервалі 3 t при зміні частоти вимушених коливань із третьою постійною швидкістю V3 від першого початкового значення X1 до першого кінцевого значення X2 для маси (ms 1m) при першій зміні інерційності коливальної системи; n 4 - число циклів вимушених коливань в часовому інтервалі 4 t при зміні частоти вимушених коливань із чет кінцевого значення X 2 для маси шостою постійною швидкістю V6 від другого початкового значення X3 до другого кінцевого значення X4 для маси (ms 2m) при другій зміні інерційності; cp1, cp2 , cp3 , cp4 , cp5 , cp6 - середні частоти діапазонів частот, що відповідають часовим інтервалам 1t, 2t, 3t, 4t, 5t, 6t, відповідно і визначаються співвідношеннями: H1 H2 cp1 B1 ; cp2 B2 ; 2 2 H3 H4 cp3 B3 ; cp 4 B 4 ; 2 2 H5 H6 cp5 B5 ; cp6 B6 , 2 2 де: B1, B3 , B5 , H1, H3 , H5 - верхні і нижні частоти діапазонів частот, що відповідають зміні амплітуди вимушених коливань від першого початкового значення X1 до першого кінцевого значення чення X4 для маси (ms 1m) при першій зміні X2 ; B2, B4 , B6 , H2, H4 , H6 - верхні і нижні частоти діапазонів частот, що відповідають зміні амплітуди вимушених коливань від другого початкового значення X3 до другого кінцевого значен інерційності; n 5 - число циклів вимушених коли ня X 4 . вертою постійною швидкістю V 4 від другого початкового значення X3 до другого кінцевого зна вань в часовому інтервалі 5 t при зміні частоти Корисна модель відноситься до області машинобудівної, авіаційної і ракетно-космічної техніки, а саме, до способів визначення інерційно жорсткістних і дисипативних параметрів нелінійних коливальних систем із кінцевим числом ступенів вільності і може знайти застосування для визна 5 чення моментів інерції механічних коливальних систем при застосуванні джерела енергії обмеженої потужності. Відомий спосіб визначення параметрів нелінійної дисипативної коливальної системи, за яким формують два режими вимушених коливань коливальної системи, в кожному режимі задають початкове і кінцеве значення амплітуди коливань нелінійної дисипативної коливальної системи, вимірюють перший і другий часові інтервали і число циклів коливань в першому і другому часових інтервалах при зміні амплітуди коливань в кожному часовому інтервалі від початкового до кінцевого значення, в першому режимі вимушених коливань нелінійної коливальної системи, частоту сигналу збуджувальної дії змінюють із постійною швидкістю V1, в другому - із постійною швидкістю V2, в режимах вимушених коливань початкові значення амплітуд коливань задають однаковими і кінцеві значення амплітуд коливань задають однаковими, вимір першого часового інтервалу і число циклів коливань в цьому інтервалі проводять при зміні частоти сигналу вимушеної дії із першою постійною швидкістю V1, вимір другого часового інтервалу і число циклів коливань в цьому часовому інтервалі проводять при зміні частоти сигналу вимушеної дії із другою постійною швидкістю V2 (V2V1, V2V1), а визначення параметра 0 проводять Із співвідношення: 0 1 ( V12 t V2 2 t )] 1 2 2 ( 1t 2 t ) [2(n1 n2 ) де: 0 - частота вільних коливань лінійної породжу вальної системи; 1t, 2t - перший і другий часові інтервали відповідно; n1, n2 - числа циклів в першому і другому часових інтервалах відповідно (Патент України на корисну модель №41550, МПК G01H11/00, 2009). Недолік відомого способу визначення параметрів нелінійної дисипативної коливальної системи при умові застосування джерела енергії, що має обмежену потужність, є можливість визначення параметрів слабо дисипативної нелінійної коливальної системи і неможливість визначення параметрів сильно дисипативної нелінійної коливальної системи при умові застосування джерела енергії, що має обмежену потужність. За прототип вибрано спосіб визначення параметрів нелінійної дисипативної коливальної системи, за яким задають перше початкове і перше кінцеве значення амплітуди затухаючих коливань нелінійної дисипативної коливальної системи, 56369 6 проводять вимір першого часового інтервалу і число циклів коливань в цьому інтервалі при зміні амплітуди затухаючих коливань від першого початкового до першого кінцевого значення, далі задають друге початкове і друге кінцеве значення амплітуди затухаючих коливань, проводять вимір другого часового інтервалу і число циклів коливань в цьому часовому інтервалі при зміні амплітуди затухаючих коливань від другого початкового до другого кінцевого значення, потім один раз змінюють інерційність нелінійної дисипативної коливальної системи і проводять вищевказану сукупність операцій по визначенню третього і четвертого часових інтервалів і чисел циклів коливань в цих часових інтервалах при зміні амплітуди коливань від її першого початкового значення до першого кінцевого значення, від другого початкового значення до другого кінцевого значення відповідно, додатково другий раз змінюють інерційність нелінійної дисипативної коливальної системи і проводять вищевказану сукупність операцій по визначенню п'ятого і шостого часових Інтервалів і чисел циклів коливань в цих часових Інтервалах при зміні амплітуди коливань від її першого початкового значення до першого кінцевого значення, від другого початкового значення до другого кінцевого значення відповідно, при цьому частоти вільних коливань лінійної дисипативної породжувальної системи і вільних коливань лінійної консервативної породжувальної системи " 1 " та " 0 " а також масу "m" коливальної системи, коефіцієнт "С" жорсткості, коефіцієнт "h" демпфування, коефіцієнт "b" опору визначають із співвідношень відповідно: [ t(n n 4 ) 4 t(n1 n 3 )] , 1 2 3 2 ( 2 t 3 t 1t 4 t ) 2 2 21m 2m 1 1 , m 2 2 2 2 2m 1 1 1m 1 1 C 2 m m2 2 2 1 1 1 1 , 1m m 0 C m 2 m m 2 2 1 1 1 1 , 1m m 2 2 h 0 1 2 m m 2 2 1 1 1 1 1m m 2 2 2 2 2 m 2 2 2 2m 1 1 1 1 1 21 1 1 41m 2m m , b 2mh 2 2 2 2 2 2 2 2 2m 1 1 1m 1 1 2m 1 1 1m 1 1 7 де 1 cm 1 h 2 , 1 c(m 1m)1 h2 , 1 c(m 2m)1 h2 , 1m , 2m , (1m 2m, 1m m, 2m 1m) - перша і друга додаткові маси; n1, n2 - числа циклів затухаючих коливань маси "m" при зміні амплітуди затухаючих коливань від першого початкового значення X1 до першого кінцевого значення X2 , від другого початкового значення X3 до другого кінцевого значення X 4 відповідно; 1t, 2 t - часові інтервали, що відповідають числам циклів n1, n2 ; n3 ,n4 - числа циклів затухаючих коливань маси ( m 1m ) при зміні амплітуди затухаючих коливань від першого початкового значення X1 до першого кінцевого значення X2 , від другого початкового значення X3 до другого кінцевого значення X 4 відповідно; 3 t, 4 t - часові інтервали, що відповідають числам n3 ,n4 циклів(періодів) коливань; n5 , n6 - числа циклів (періодів) затухаючих коливань маси (m 2m) при зміні амплітуди затухаючих коливань від першого початкового значення X1 до першого кінцевого значення X2 , від другого початкового значення X3 до другого кінцевого значення X 4 відповідно; 5 t, 6 t - часові інтервали, що відповідають числам n5 , n6 циклів коливань (Патент України на корисну модель №45033, МПК G01H11/00, 2009). Недолік відомого способу визначення параметрів нелінійної дисипативної коливальної системи є можливість визначення параметрів сильно дисипативної нелінійної коливальної системи при застосуванні ідеального джерела енергії і неможливість визначення параметрів сильно дисипативної нелінійної коливальної системи при застосуванні джерела енергії обмеженої потужності. В основу корисної моделі поставлене завдання удосконалення способу визначення параметрів нелінійної дисипативної коливальної системи шляхом визначення параметрів нелінійної сильно дисипативної коливальної системи при застосуванні джерела енергії обмеженої потужності за рахунок формування нового алгоритму на підставі отриманих нових аналітичних співвідношень, що і розширює функціональні можливості способу і область його використання. Поставлене завдання вирішується тим, що в способі визначення параметрів нелінійної дисипа 56369 8 тивної коливальної системи, за яким формують шість режимів коливань нелінійної дисипативної коливальної системи, в першому і другому режимах задають перше початкове і перше кінцеве, друге початкове і друге кінцеве значення амплітуди коливань відповідно, вимірюють перший і другий часові інтервали І числа циклів коливань в першому і другому часових інтервалах відповідно, перший раз змінюють інерційність нелінійної дисипативної коливальної системи і проводять вищевказану сукупність операцій по визначенню третього і четвертого часових інтервалів і чисел циклів коливань в цих часових інтервалах при зміні амплітуди коливань від першого початкового значення до першого кінцевого значення, від другого початкового значення до другого кінцевого значення відповідно, другий раз змінюють інерційність нелінійної дисипативної коливальної системи і проводять вищевказану сукупність операцій по визначенню п'ятого і шостого часових інтервалів і чисел циклів коливань в цих часових інтервалах при зміні амплітуди коливань від першого початкового значення до першого кінцевого значення, від другого початкового значення до другого кінцевого значення, згідно з корисною моделлю, шість режимів коливань формують, як режими вимушених коливань, в кожному із шести режимів коливань фіксують значення нижніх і верхніх частот діапазонів частот, що відповідають змінам амплітуд вимушених коливань від першого початкового значення до першого кінцевого значення в першому, третьому і п'ятому режимах, від другого початкового до другого кінцевого значення в другому, четвертому і шостому режимах, причому зміну частоти сигналу вимушеної дії проводять із першою, другою, третьою, четвертою, п'ятою і шостою швидкостями для першого, другого, третього, четвертого, п'ятого, шостого режимів відповідно, а значення частот 0s вільних коливань лінійної породжувальної системи, інерційно-жорсткісних параметрів ms, сs по S-ій нормальній координаті визначають на підставі співвідношень: 2 2 (1s 1s ) ; ms 2 2 2 2 1s 1s 1s 1s 1m 2m 2 cs 2 (1s 1s )m s (ms 1m) 1m або 2 (2 1s )m s (m s 2m) ; c s 1s 2m 9 56369 10 2 2 0s 2 cs (2 1s )(m s 1m) m 2 1s (1s 1s )1 s ms 1m 1m 2 0 s 2 cs (2 1s )( m s 2m) m 2 1s (1s 1s )1 s ms 2m 2m або 2 де: 1s або , або ( 2 t 3 t 1t 4 t ) 5 t 2(n4 n6 ) cp 4 4 t cp6 6 t 6 t 2(n3 n5 ) cp3 3 t cp5 5 t ( 4 t 5 t 3 t 6 t ) 1t 2(n2 n6 ) cp2 2t cp6 6 t 6 t 2(n1 n5 ) cp11t cp5 5 t 3 t 2(n4 n6 ) cp 4 4 t cp6 6 t 6 t 2(n3 n5 ) cp3 3 t cp5 5 t ( 4 t 5 t 3 t 6 t ) , або ( 2t 5 t 1t 6 t ) , льної системи; n 4 - число циклів вимушених коли 1s c sms1 h2 , s вань в часовому інтервалі 4 t при зміні частоти вимушених коливань із четвертою постійною швидкістю V4 від другого початкового значення X3 і 2 1s c s (ms 1m)1 hs , 2 1s c s (m s 2m) 1 h s , до другого кінцевого значення X 4 1m, 2m(1m 2m, 1m ms , 2m ms ) перша І друга додаткові маси відповідно; n1 - число циклів вимушених коливань в часовому інтервалі 1t при зміні частоти вимушених коливань із першою постійною швидкістю V1 від першого початкового значення X1 до першого кінцевого значення X2 для маси ms ; n 2 - число циклів вимушених коливань в часовому інтервалі 2 t при зміні частоти вимушених коливань із другою постійною швидкістю V2 від другого початкового значення X3 до другого кінцевого значення X 4 для маси ms ; n 3 - число циклів вимушених коливань в часовому інтервалі 3 t при зміні частоти вимушених коливань із третьою постійною швидкістю V3 від першого початкового значення X1 до кінцевого ( 2t 5 t 1t 6 t ) 1s першого 5 t 2(n2 n6 ) cp2 2t cp6 6 t 6 t 2(n1 n5 ) cp11t cp5 5 t 1t 2(n2 n4 ) cp2 2t cp4 4 t 2 t 2(n1 n3 ) cp11t cp3 3 t 1s 1s ( 2 t 3 t 1t 4 t ) 1s 1s 3 t 2(n2 n4 ) cp2 2 t cp 4 4 t 4 t 2(n1 n3 ) cp11t cp3 3 t значення X2 для маси (ms 1m) при першій зміні Інерційності колива для маси (ms 1m) при першій зміні інерційності; n 5 - число циклів вимушених коливань в часовому інтервалі 5 t при зміні частоти вимушених коливань із п'ятою постійною швидкістю V5 від першого початкового значення X1 до першого кінцевого значення X2 для маси (ms 2m) при другій зміні інерційності; n 6 - число циклів вимушених коливань в часовому інтервалі 6 t при зміні частоти вимушених коливань із шостою постійною швидкістю V6 від другого початкового значення X3 до другого кінцевого (ms 2m) при значення другій cp1, cp2 , cp3 , cp4 , cp5 , cp6 X4 зміні для маси інерційності; - середні частоти діапазонів частот, що відповідають часовим інтервалам 1t, 2 t, 3 t, 4 t, 5 t, 6 t, відповідно і визначаються співвідношеннями: H1 H2 ; cp2 B2 ; cp1 B1 2 2 11 56369 ною коливальною системою при застосуванні асимптотичного методу Крилова-БоголюбоваМитропольського система рівнянь першого наближення приймає вигляд B3 H3 H4 ; cp 4 B 4 ; 2 2 H5 H6 ; cp6 B6 , cp5 B5 2 2 де: B1, B3 , B5 , H1, H3 , H5 - верхні і нижні частоти діапазонів частот, що відповідають зміні амплітуди вимушених коливань від першого початкового значення X1 до першого кінцевого знаcp3 dXa hs Xa A1( Xa ) exp(hs t ), (1) dt d 1s cp B1( Xa ), dt 2 де: 1s 2 h2 , cp - середня частота по діs s апазону частот зміни амплітуди коливань. (Пресняков В.К., Филер З.Е. Колебания механической системы, рассматриваемой совместно с двигателем. «Динамика и прочность машин», Харьков, изд-во Харьковского университета, - 1971. С.82; Кононенко В.О. Колебательные системы с ограниченным возбуждением, М.: «Наука», - 1964. С.30-35, 51-58; Кононенко В.О. Нелинейные колебания механических систем. Киев: «Наукова думка», - 1980. С.90-93, 95-100, 126-130, 201-210; патент №45033 України. МПК G01H11/00; Бюл. №20, 2009р.). Система рівнянь (1) відповідає коливальній системі, диференційне рівняння для якої належить до класу чення X2 ; B2 , B4 , B6 , H2 , H4 , H6 - верхні і нижні частоти діапазонів частот, що відповідають зміні амплітуди вимушених коливань від другого початкового значення X3 до другого кінцевого значення X 4 . Застосування запропонованого способу визначення параметрів нелінійної дисипативної коливальної системи разом з усіма суттєвими ознаками, включаючи відмінні, забезпечує можливість визначення інерційно-жорсткістних параметрів шляхом формування нового алгоритму проведення операцій по проведенню вимірювань в режимах вимушених коливань, що забезпечує розширення функціональних можливостей за рахунок визначення параметрів сильно дисипативної коливальної системи при застосуванні джерела енергії обмеженої потужності. Розробка нового алгоритму визначення параметрів нелінійної дисипативної коливальної системи базується на наступних теоретичних аналітичних перетвореннях. Для випадку урахування взаємодії джерела енергії обмеженої потужності із сильнодисипатив d 1s t cp t exp(ht) ( xa ) 12 d2 x dx dx 2 0s x f ( x, ) , (2) dt dt dt рішення якого X Xa sin . Із системи рівнянь (1) отримаємо таке рівнян2 2hs ня B1 ( X a ) A 1( X a ) dXa B1 ( X a ) X a h exp(ht) A (t) 1( X a ) dt . (3) На підставі співвідношення (3) отримаємо систему рівнянь 2n1 1s 1t cp1 1t xa2 exp(ht) x a1 2n 2 1s 2 t cp2 2 t B1( X a ) A 1( X a ) xa 4 exp(ht) xa3 2n 3 1s 3 t cp3 3 t xa2 exp(ht) x a1 2n 4 1s 4 t cp 4 4 t xa4 exp(ht) xa2 2n 5 1s 5 t cp5 5 t xa2 exp(ht) x a1 2n 6 1s 6 t cp6 6 t xa4 xa3 де 1s c sms1 h2 , s exp(ht) t2 dX a X a exp(ht) B1( X a ) A 1( X a ) B1( X a ) A 1( X a ) B1( X a) A 1( X a ) B1( X a ) A 1( X a ) B1( X a ) A 1( X a ) t1 B1( X a ) A 1( X a ) t4 dX a X a exp(ht) t3 t6 dX a X a exp(ht) t5 t8 dX a X a exp(ht) t7 dX a t10 B1( X a) A 1( X a ) B1( X a ) A 1( X a ) B1( X a ) A 1( X a ) B1( X a ) X a exp(ht) A t9 dX a t12 1( X a ) B1( X a ) X a exp(ht) A t11 dt , (4) 1( X a ) dt , (5) dt , (6) dt , (7) dt , (8) dt , (9) 2 1s c s (m s 2m) 1 h s , (10) 2 1s c s (ms 1m)1 hs , де: 1m, 2m(1m 2m, 1m ms , 2m ms ) перша і друга додаткові маси відповідно; n1 - чис 13 56369 ло циклів вимушених коливань в часовому інтервалі 1t при зміні частоти вимушених коливань із 14 першою постійною швидкістю V1 від першого по вань в часовому інтервалі 6 t при зміні частоти вимушених коливань із шостою постійною швидкістю V6 від другого початкового значення X3 до чаткового значення X1 до першого кінцевого другого значення X2 для маси ms ; n 2 - число циклів (ms 2m) вимушених коливань в часовому інтервалі 2 t при зміні частоти вимушених коливань із другою постійною швидкістю V2 від другого початкового cp1, cp2 , cp3 , cp4 , cp5 , cp6 - середні частоти діапазонів частот, що відповідають часовим інтервалам 1t, 2 t, 3 t, 4 t, 5 t, 6 t відповідно і визначаються співвідношеннями: H1 H2 ; cp2 B2 ; cp1 B1 2 2 H3 H4 ; cp 4 B 4 ; cp3 B3 2 2 H5 H6 ; cp6 B6 , cp5 B5 2 2 де: B1, B3 , B5 , H1, H3 , H5 - верхні і нижні частоти діапазонів частот, що відповідають зміні амплітуди вимушених коливань від першого початкового значення X1 до першого кінцевого значення значення X3 до другого кінцевого значення X 4 для маси ms ; n 3 - число циклів вимушених коливань в часовому інтервалі 3 t при зміні частоти вимушених коливань із третьою постійною швидкістю V2 від першого початкового значення X1 до першого кінцевого значення X2 для маси (ms 1m) при першій зміні інерційності коливальної системи; n 4 - число циклів вимушених коливань в часовому інтервалі 4 t при зміні частоти вимушених коливань із четвертою постійною швидкістю V4 від другого початкового значення X3 до другого кінцевого значення X 4 для маси (ms 1m) при першій зміні інерційності; n 5 - число циклів вимушених коливань в часовому інтервалі 5 t при зміні частоти вимушених коливань із п'ятою постійною швидкістю V5 від першого початкового значення X1 до першого кінцевого значення X2 для маси (ms 2m) при другій зміні інерційності; n 6 - число циклів вимушених коли кінцевого при значення другій X4 зміні для маси інерційності; X2 ; B2 , B4 , B6 , H2 , H4 , H6 - верхні і нижні частоти діапазонів частот, що відповідають зміні амплітуди вимушених коливань від другого початкового значення X3 до другого кінцевого значення X 4 . Після нескладних перетворень системи рівнянь (4)-(9) отримаємо такі рівняння для визначення частот 1s , 1s , 1s , а саме: 1) із першого (4) і третього (6), другого (5) і четвертого (7) рівнянь отримаємо таку систему рівнянь: 2n1 1s 1t cp11t 2n3 1s 3 t cp3 3 t, (11) 2n2 1s 2 t cp2 2 t 2n 4 1s 4 t cp4 4 t; 2) із першого (4) і п'ятого (8), другого (5) і шостого (9) рівнянь отримаємо таку систему рівнянь: 2n1 1s 1t cp11t 2n5 1s 5 t cp5 5 t, (12) 2n 2 1s 2 t cp2 2 t 2n 6 1s 6 t cp6 6 t; 3) із третього (6) і п'ятого (8), четвертого (7) і шостого (9) рівнянь отримаємо таку систему рівнянь: 2n1 1s 3 t cp3 3 t 2n5 1s 5 t cp5 5 t, (13) 2n 4 1s 4 t cp 4 4 t 2n 6 1s 6 t cp6 6 t; Із (11) маємо таку систему двох рівнянь 1s 1t 1s 3 tt 2(n1 n3 ) cp11t cp3 3 t, (14) 1s 1t 1s 3 tt 2(n1 n3 ) cp11t cp3 3 ; Із (12) маємо таку систему двох рівнянь: 1s 1t 1s 5 t 2(n1 n5 ) cp11t cp5 5 t, (15) 1s 2 t 1s 6 t 2(n1 n 6 ) cp2 2 t cp6 6 t; Із (І3) маємо таку систему двох рівнянь: 1s 1t 1s 3 tt 2(n1 n3 ) cp11t cp3 3 t, (16) 1s 1t 1s 3 tt 2(n1 n3 ) cp11t cp3 3 ; 15 56369 16 Із (14) отримаємо аналітичні співвідношення для визначення частот 1s , 1s 3t[2(n2 n4 ) cp22t cp44t] 4t[2(n1 n3 ) cp11t cp33t] 1s , (17) (2t3t 1t4t ) 1s 1t[2(n2 n4 ) cp22t cp44t] 2t[2(n1 n3 ) cp11t cp33t] (18) ( 2t3t 1t4t ) Із (15) отримаємо аналітичні співвідношення для визначення частот 1s , 1s 5t[2(n2 n6 ) cp22t cp66t] 6t[2(n1 n5 ) cp11t cp55t] 1s , (19) ( 2t5t 1t6t ) 1s 1t[2(n2 n6 ) cp22t cp66t] 6t[2(n1 n5 ) cp11t cp55t] ( 2t5t 1t6t ) . (20) Із (16) отримаємо аналітичні співвідношення для визначення частот 1s , 1s 1s 1s 5t[2(n4 n6 ) cp44t cp66t] 6t[2(n3 n5 ) cp33t cp55t] ( 4t5t 3t6t ) , (21) 3t[2(n4 n6 ) cp44t cp66t] 6t[2(n3 n5 ) cp33t cp55t] , (22) ( 4t5t 3t6t ) На підставі (10), (17), (18), (19), (20), (21), (22) 2 2 (1s 1s )m s (ms 1m) отримаємо аналітичні співвідношення для визна(24) cs 1m чення інерційно-жорсткісних параметрів 2 або 2 (1s 1s ) 2 ; (23) ms 2 (1s 1s )m s (m s 2m) 2 2 2 2 ; (25) cs 1s 1s 1s 1s 2m 1m 2m 2 2 0s 2 cs (2 1s )(m s 1m) m 2 1s (1s 1s )1 s (26) ms 1m 1m 2 0 s 2 cs ( 2 1s )( m s 1m) ms 2 . (22) 1s (1s 1s )1 ms 1m 2m або 2 Спосіб визначення параметрів нелінійної сильнодисипативної коливальної системи при застосуванні джерела енергії обмеженої потужності реалізують на підставі наступного алгоритму. 1) Формують шість режимів вимушених коливань нелінійної дисипативної коливальної системи, в першому, другому, третьому, четвертому, п'ятому і шостому режимах частоту сигналу вимушеної дії змінюють із постійними швидкостями V1, V2, V3, V4, V5, V6 відповідно. 2) В кожному режимі фіксують і реєструють часові інтервали і числа циклів (періодів) коливань у відповідному часовому інтервалі. 3) В першому, третьому і п'ятому режимах часові інтервали і числа циклів коливань фіксують і реєструють при зміні амплітуди вимушених коливань від першого початкового значення до першого кінцевого значення, у другому, четвертому і шостому режимах часові інтервали і числа циклів коливань фіксують і реєструють при зміні амплітуди вимушених коливань від другого початкового значення до другого кінцевого значення. 4) В кожному режимі фіксують і реєструють нижні і верхні частоти діапазонів частот, що відпо відають зміні амплітуди від початкового значення до кінцевого значення. 5) Перший і другий режими вимушених коливань формують без зміни інерційності коливальної системи масою «ms». 6) Третій і четвертий режими вимушених коливань формують після першої зміни інерційності коливальної системи для маси (ms 1m) за рахунок жорсткого з'єднання маси «ms» коливальної системи з першого додаткового масою 1m при умові 1m ms . 7) П'ятий і шостий режими вимушених коливань формують після другої зміни інерційності коливальної системи для маси (ms 2m) за рахунок жорсткого з'єднання маси «m» коливальної системи з другою додатковою масою 2m при умові 2m ms , 2m 1m . Новим в реалізації визначення параметрів сильно дисипативної коливальної системи при застосуванні джерела енергії обмеженої потужності є: 17 56369 1) формування шести режимів вимушених коливань нелінійної дисипативної коливальної системи; 2) в кожному із шести режимів коливань фіксують і реєструють значення верхніх і нижніх частот кожного із шести діапазонів частот, які визначають відповідно зміні амплітуди вимушених коливань від відповідних початкових значень до відповідних кінцевих значень. Спосіб визначення параметрів нелінійної дисипативної коливальної системи реалізують наступним чином. 1) Установлюють випробуваний об'єкт (конструкцію) на рухомій платформі вібростенда, зокрема, електродинамічного типу. 2) Послідовно реалізують шість режимів вимушених коливань, перший і другий режими формують без зміни інерційності сильнодисипативної нелінійної коливальної системи, третій і четвертий режими формують при першій зміні інерційності коливальної системи, п'ятий і шостий режими формують при другій зміні інерційності коливальної системи. Першу зміну інерційності формують шляхом жорсткого з'єднання з масою «ms» коливальної системи першої додаткової маси 1m при умові 1m ms . Другу зміну інерційності формують шляхом жорсткого з'єднання з масою «ms» коливальної системи другої додаткової маси 2m при умові 2m ms . 3) У першому, третьому і п'ятому режимах фіксують і реєструють відповідні часові інтервали і Комп’ютерна верстка О. Рябко 18 числа циклів коливань в цих часових інтервалах при зміні амплітуди вимушених коливань від першого початкового значення до першого кінцевого значення при зміні частоти сигналу вимушеної дії з першою, третьою і п'ятою швидкостями відповідно. 4) У другому, четвертому і шостому режимах фіксують і реєструють відповідні часові інтервали і числа циклів коливань в цих часових інтервалах при зміні амплітуди вимушених коливань від другого початкового значення до другого кінцевого значення при зміні частоти сигналу вимушеної дії із другою, четвертою і шостою швидкостями відповідно. 5) В першому-шостому режимах проводять фіксацію І реєстрацію нижніх і верхніх частот шести діапазонів частот відповідно. Як відомо для випадку сильнодисипативної нелінійної коливальної системи при застосуванні асимптотичного методу Крилова-Боголюбова-Митропольського (КБМ) із рівнянь першого наближення визначають не частоту вільних коливань лінійної консервативної системи, а частоту вільних коливань лінійної дисипативної коливальної системи. 6) За допомогою обчислювальновимірювального комплексу (комп'ютерної системи) проводять обробку зареєстрованих сигналів 1t, 2 t, 3 t, 4 t, 5 t, 6 t , вимушених коливань від другого початкового значення X3 до другого кінцевого значення X 4 . Підписне Тираж 26 прим. Міністерство освіти і науки України Державний департамент інтелектуальної власності, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601
ДивитисяДодаткова інформація
Назва патенту англійськоюMethod for determination of parameters of non-linear dissipative oscillatory system
Автори англійськоюPuz'ko Ihor Danylovych
Назва патенту російськоюСпособ определения параметров нелинейной диссипативной колебательной системы
Автори російськоюПузько Игорь Данилович
МПК / Мітки
МПК: G01H 11/00
Мітки: системі, визначення, дисипативної, спосіб, параметрів, коливальної, нелінійної
Код посилання
<a href="https://ua.patents.su/9-56369-sposib-viznachennya-parametriv-nelinijjno-disipativno-kolivalno-sistemi.html" target="_blank" rel="follow" title="База патентів України">Спосіб визначення параметрів нелінійної дисипативної коливальної системи</a>
Попередній патент: Спосіб лікування хворих на хронічну серцеву недостатність коронарогенного генезу з супутньою анемією
Наступний патент: Спосіб переробки твердих побутових відходів
Випадковий патент: Пристрій для руйнування монолітних об'єктів












