Спосіб збереження в пам`яті потокового графа алгоритму у формі структурної матриці

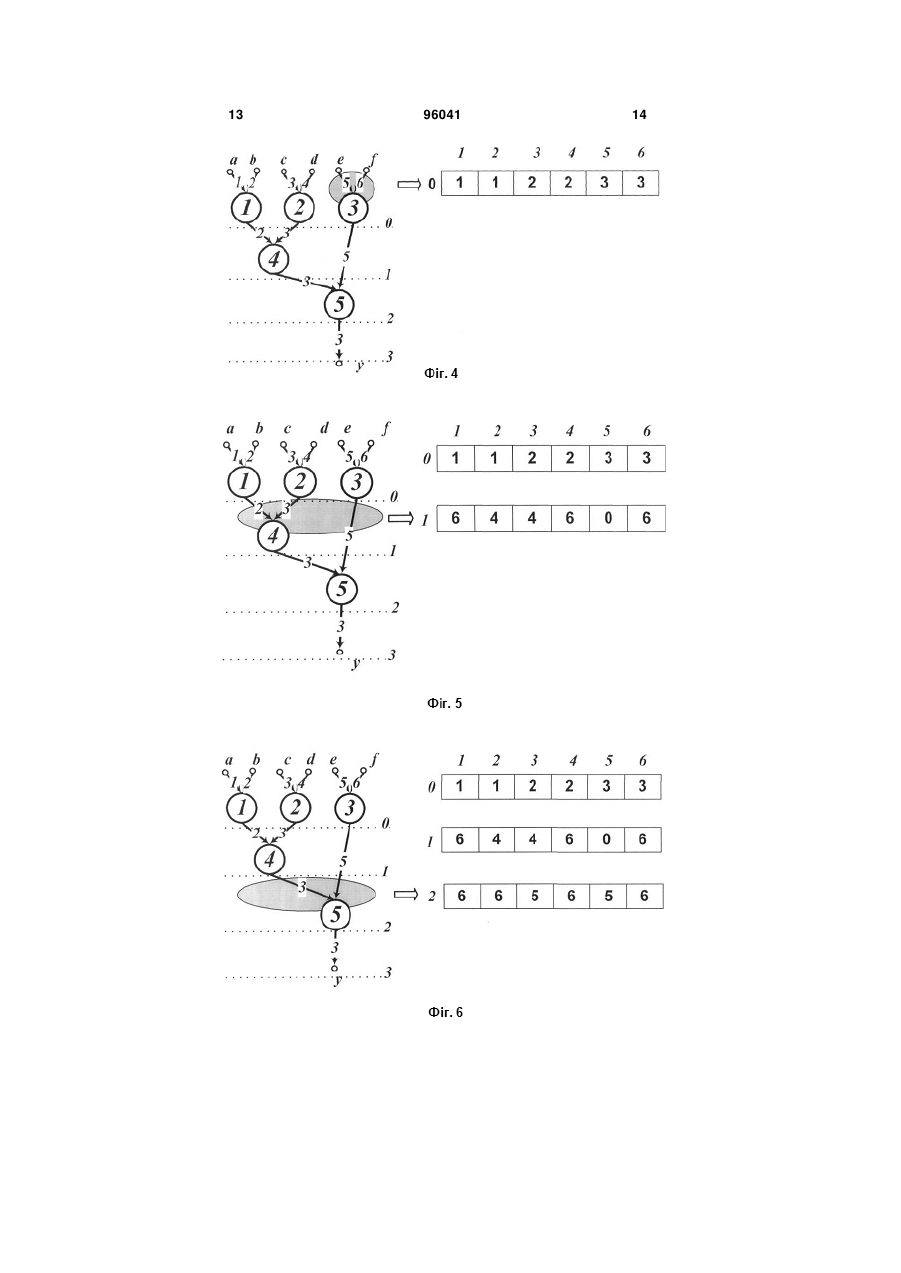
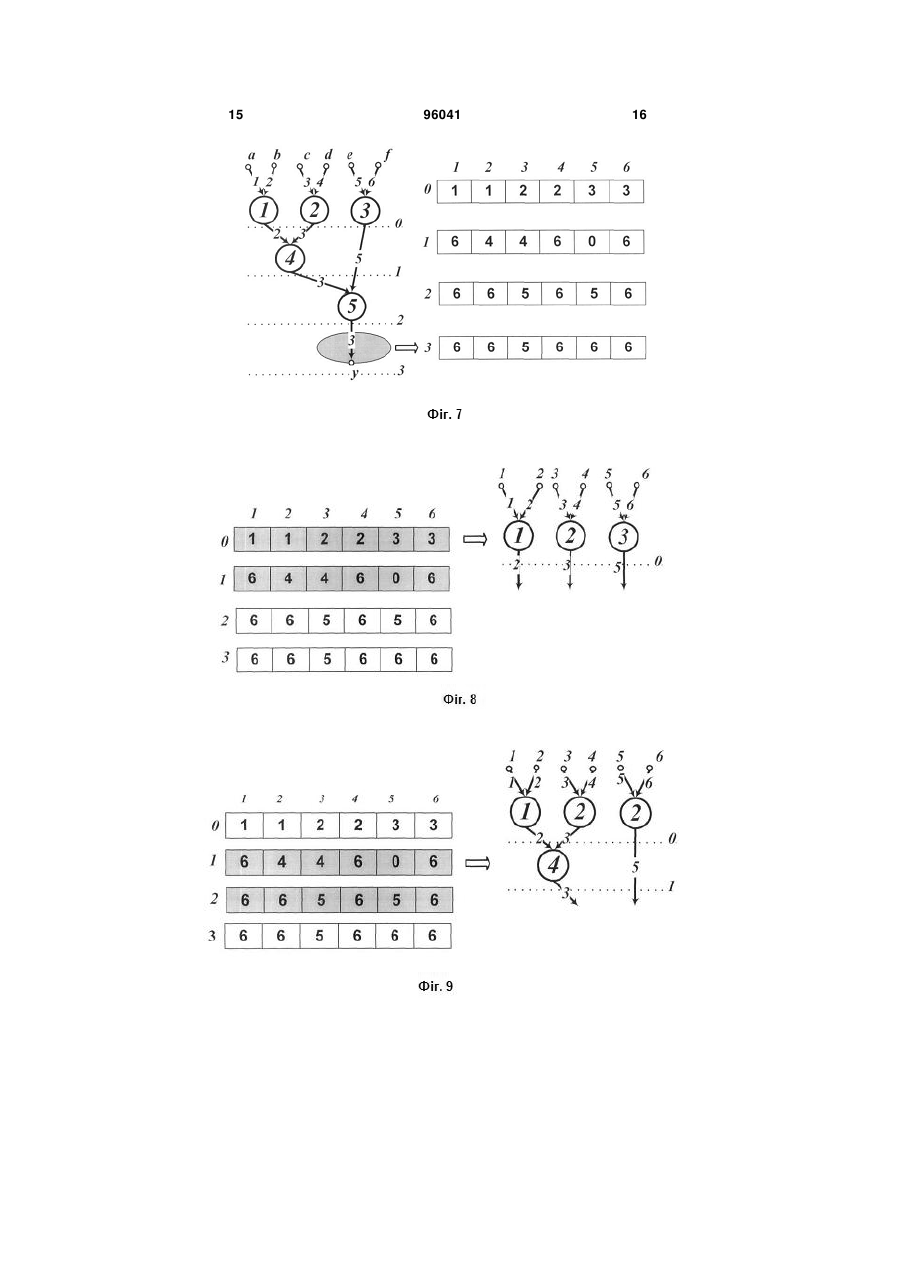
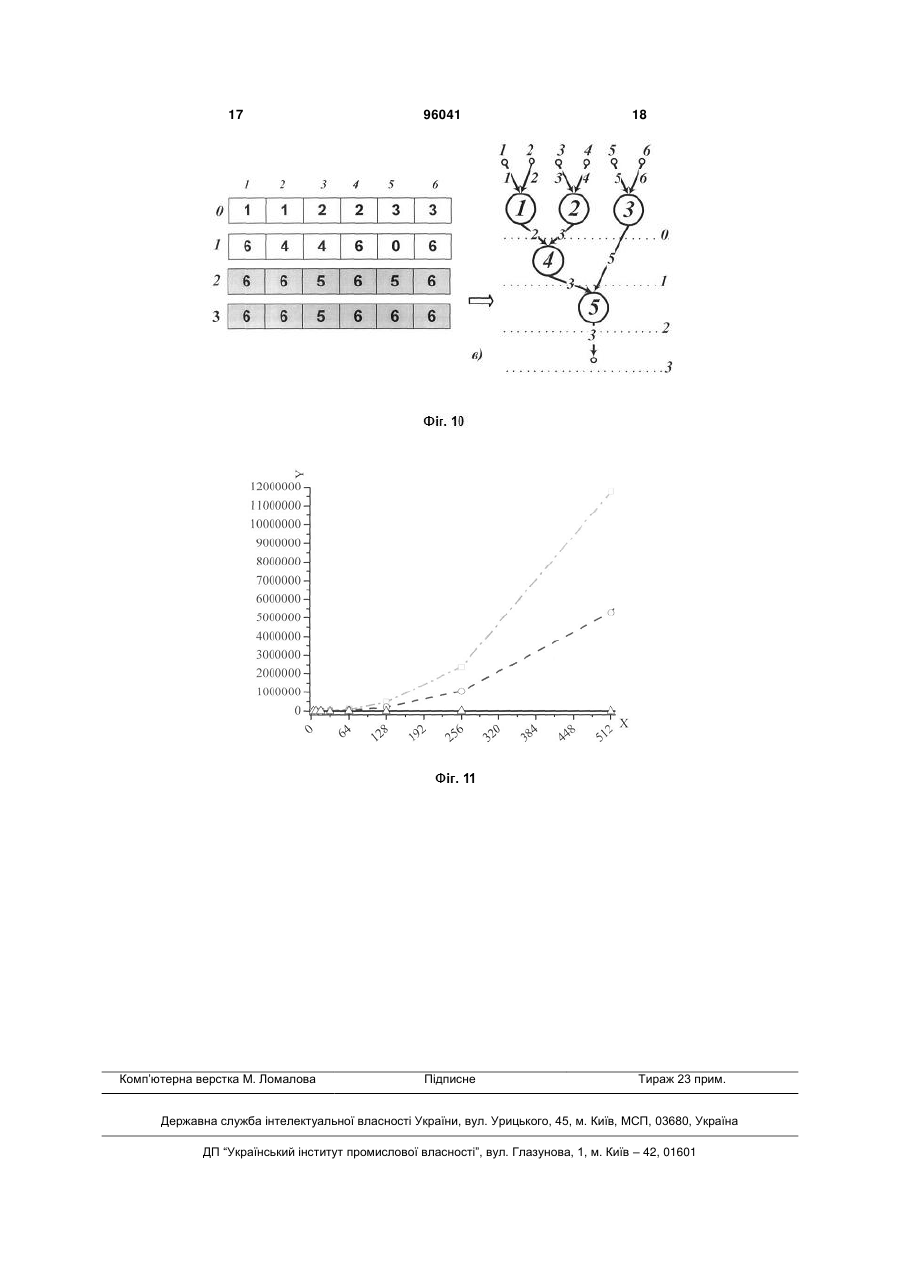
Спосіб збереження в пам'яті потокового графа алгоритму у формі структурної матриці, який складається з етапу маркування графа алгоритму, етапу запису інформації та етапу зчитування інформації, причому, на етапі маркування графа алгоритму здійснюють нумерацію вершин потокового графа алгоритму числами від 1 до N, де N кількість вершин потокового графа алгоритму, та нумерацію дуг потокового графа алгоритму, на етапі запису інформації здійснюють перегляд потокового графа алгоритму та запис інформації до комірок пам'яті, на етапі зчитування інформації здійснюють зчитування вмісту комірок пам'яті та побудову потокового графа алгоритму, причому спочатку будують та нумерують цифрами від 1 до N вершини графа алгоритму, далі зчитують вміст комірок пам'яті та з'єднують вершини потокового графа алгоритму дугами, який відрізняється тим, що на етапі маркування вершини розподіляють по l ярусах таким чином, що в i  му ярусі 2 3 96041 4 дить в цю вершину, якщо вмістом комірки ij є число, що входить до множини номерів вершин і вміс містить значення 0, тобто перетинає i  й ярус і не надходить в жодну вершину даного ярусу, то в i  му ярусі дугу з номером j продовжують до наступного ярусу, та виконують дані дії до тих пір, доки не буде зчитано вміст всіх комірок пам'яті та відображені всі дуги та вершини графа алгоритму. Винахід належить до області обчислювальної техніки і може бути використаний при виконанні опрацювання інформації. Відомий спосіб збереження в пам'яті графа алгоритму у формі матриці суміжності [1], який передбачає виконання етапу маркування графа алгоритму, етапу запису інформації та етапу зчитування інформації, причому, на етапі маркування графа алгоритму здійснюють нумерацію вершин графа алгоритму числами від 1 до N, де N - кількість вершин графа алгоритму, на етапі запису інформації здійснюють перегляд графа алгоритму комірки (і) містить перелік вершин, то вершину і з'єднують дугами з вершинами з даного переліку. Кількість комірок пам'яті, необхідних для збереження графа алгоритму даним способом, рівна сумі кількості вершин та дуг графа алгоритму. Недоліком відомого способу збереження в пам'яті графа алгоритму у формі списку суміжності є неможливість збереження потокового графа алгоритму, оскільки цей спосіб не забезпечує розподіл та закріплення вершин за ярусами графа алгоритму та необхідність виконання великої кількості кроків для отримання множини вершин, які є суміжними з даною вершиною. Відомий спосіб збереження в пам'яті графа алгоритму у формі символьної матриці [3], який передбачає виконання етапу маркування графа алгоритму, етапу запису інформації та етапу зчитування інформації, причому, на етапі маркування графа алгоритму здійснюють нумерацію вершин графа алгоритму числами від 1 до N, де N - кількість вершин графа алгоритму, та нумерацію дуг графа алгоритму парою чисел, що відповідають номерам вершин, які є початком і кінцем даної дуги, на етапі запису інформації здійснюють перегляд графа алгоритму та запис в комірку том комірки i  1 , j є число, що входить до множини номерів вершин, або дорівнює 0, то в i  му ярусі відображають дугу з номером j , що виходить з даної вершини, якщо вміст комірки ij та запис в комірку (i, j) (i  1 N, j  1 N) пам'яті зна, , чення кількості дуг a (a  1 n) , n - кількість вхідних , дуг графа), що з'єднують вершини і тa j, які є суміжними, і вершина і є початком для даних дуг, та нуля в інших випадках, на етапі зчитування інформації здійснюють зчитування вмісту комірок пам'яті та побудову графа алгоритму, причому спочатку будують та нумерують цифрами від 1 до N вершини графа алгоритму, далі зчитують вміст комірок (i, j) пам'яті та, якщо вміст комірки (i, j) пам'яті рівний а, вершини і тa j з'єднують а дугами, інакше, якщо вміст комірки (i, j) пам'яті рівний нулю, вершини і тa j дугами не з'єднують. Кількість комірок пам'яті, необхідних для збереження графа алгоритму даним способом, рівна квадрату кількості N вершин графа алгоритму. Недоліком відомого способу збереження в пам'яті графа алгоритму у формі матриці суміжності є потреба у великому об'ємі пам'яті та неможливість збереження потокового графа алгоритму, оскільки цей спосіб не забезпечує розподіл та закріплення вершин за ярусами графа алгоритму. Відомий спосіб збереження в пам'яті графа алгоритму у формі списку суміжності [2], який передбачає виконання етапу маркування графа алгоритму, етапу запису інформації та етапу зчитування інформації, причому, на етапі маркування графа алгоритму здійснюють нумерацію вершин графа алгоритму числами від 1 до N, де N - кількість вершин графа алгоритму, на етапі запису інформації здійснюють перегляд графа алгоритму та запис в комірку (i) (i  1 N) пам'яті номерів всіх , вершин, що є суміжними з вершиною і, та на етапі зчитування інформації здійснюють зчитування вмісту комірок пам'яті та побудову графа алгоритму, причому спочатку будують та нумерують цифрами від 1 до N вершини графа алгоритму, далі зчитують вміст комірок (і) пам'яті та, якщо вміст (i) (i  1 N) , пам'яті одиниці, а в комірки (i, j) (i  1 N, j  1 N) пам'яті символьного позначення , , дуги a(i, j) , якщо вершина і зв'язана дугою a(i, j) з вершиною j і є її початком, запис в комірку пам'яті (i, j) заперечення символьного позначення дуги a(i, j) , що відзначається рискою зверху (a(i, j)) , якщо вершина i зв'язана дугою a(i, j) з вершиною j і є її кінцем, та запис в комірку (i, j) пам'яті нуля, якщо вершини і та j не зв'язані, на етапі зчитування інформації здійснюють зчитування вмісту комірок пам'яті та побудову графа алгоритму, причому спочатку будують та нумерують цифрами від 1 до N вершини графа алгоритму, далі зчитують вміст комірок (i, j) пам'яті та, якщо вміст комірки (i, j) пам'яті містить символьне позначення дуги a(i, j) , тоді до вершини i, що є початком дуги, приєднують дугу, що з'єднує дану вершину з вершиною j та проставляють її номер, якщо вміст комірки (i, j) пам'яті відзначається рискою зверху (a(i, j)) , до вершини i, що є кінцем дуги приєднують дугу від вершини j та проставляють номер дуги, інакше, якщо вміст комірки (i, j) пам'яті рівний нулю або одиниці, вершини і та j дугою не з'єднують. 5 Кількість комірок пам'яті, необхідних для збереження графа алгоритму даним способом, рівна квадрату кількості N вершин графа алгоритму. Недоліком відомого способу збереження в пам'яті графа алгоритму у формі символьної матриці є потреба у великому об'ємі пам'яті та неможливість збереження потокового графа алгоритму, оскільки цей спосіб не забезпечує розподіл та закріплення вершин за ярусами графа алгоритму. Найближчим до винаходу є спосіб збереження в пам'яті графа алгоритму у формі матриці інциденцій [4], який передбачає виконання етапу маркування графа алгоритму, етапу запису інформації та етапу зчитування інформації, причому, на етапі маркування графа алгоритму здійснюють нумерацію вершин графа алгоритму числами від 1 до N, де N - кількість вершин графа алгоритму, та нумерацію дуг графа алгоритму числами від 1 до М, де М - кількість дуг графа алгоритму, на етапі запису інформації здійснюють перегляд графа алгоритму та запис в комірку ( j, i) ( j  1 M, i  1 N) пам'яті одини, , ці, якщо вершина інцидентна дузі і є її початком, запис в комірку (j,i) пам'яті мінус одиниці, якщо вершина інцидентна дузі і є її кінцем, та запис в комірку (i, j) пам'яті нуля, якщо вершина та дуга не інцидентні, на етапі зчитування інформації здійснюють зчитування вмісту комірок пам'яті та побудову графа алгоритму, причому спочатку будують та нумерують цифрами від 1 до N вершини графа алгоритму, далі зчитують вміст комірок (i, j) пам'яті та, якщо вміст комірки (i, j) пам'яті рівний одиниці, до вершини i, що є початком дуги, приєднують дугу j та проставляють її номер, якщо вміст комірки (i, j) пам'яті рівний мінус одиниці, до вершини і, що є кінцем дуги, приєднують дугу j та проставляють її номер, інакше, якщо вміст комірки (i, j) пам'яті рівний нулю, дугу j до вершини i не приєднують. Кількість комірок пам'яті, необхідних для збереження графа алгоритму даним способом, рівна добутку кількості вершин та дуг графа алгоритму. Недоліком відомого способу збереження в пам'яті графа алгоритму у формі матриці інциденцій є потреба у великому об'ємі пам'яті та неможливість збереження потокового графа алгоритму, оскільки цей спосіб не забезпечує розподіл та закріплення вершин за ярусами графа алгоритму. В основу винаходу поставлена задача зменшити об'єм пам'яті, необхідний для збереження графа алгоритму, та розширити функціональні можливості за рахунок забезпечення розподілу та закріплення вершин за ярусами графа алгоритму. Поставлена задача вирішується тим, що в способі збереження в пам'яті потокового графа алгоритму у формі структурної матриці, який передбачає виконання етапу маркування графа алгоритму, етапу запису інформації та етапу зчитування інформації, причому, на етапі маркування графа алгоритму здійснюють нумерацію вершин потокового графа алгоритму числами від 1 до N, де N - кількість вершин потокового графа алгоритму, та нумерацію дуг потокового графа алгоритму, на етапі запису інформації здійснюють перегляд потокового графа алгоритму та запис інформації 96041 6до комірок пам'яті, на етапі зчитування інформації здійснюють зчитування вмісту комірок пам'яті та побудову потокового графа алгоритму, причому спочатку будують та нумерують цифрами від 1 до N вершини графа алгоритму, далі зчитують вміст комірок пам'яті та з'єднують вершини потокового графа алгоритму дугами, відповідно до винаходу на етапі маркування вершини розподіляють по l ярусах таким чином, що в z-му ярусі (i  0, l  1) розміщені тільки вершини, на які надходять дуги від вершин попередніх ярусів і не надходять від вершин того ж ярусу та наступних ярусів, нумерацію ярусів починають з ярусу, на якому виконуються операції над вхідними даними і закінчують ярусом, в якому знаходяться вихідні дуги потокового графа алгоритму, а нумерацію дуг розпочинають з першого ярусу, і кожній вхідній дузі даного ярусу привласнюють натуральне число j( j  1 n) , а від , нього вниз за правилом: вихідним дугам привласнюють довільне значення із множини натуральних чисел, що привласнені дугам, які входять в дану вершину, причому кількість вхідних дуг будь-якої вершини графа k(k  1 N) дорівнює a(a  1 n) , а , , кількість вихідних дуг будь-якої вершини k дорівнює b(b  1 n) , n - кількість вхідних дуг графа, при, чому для кожної вершини повинна виконуватися нерівність a  b , на етапі запису інформації здійснюють перегляд всіх дуг j( j  1 n) кожного ярусу , i (i  0, l  1) та в комірку ij пам'яті записують номер вершини k, в яку надходить дана дуга j, або 0, якщо в даному i-му ярусі вона не надходить в жодну з вершин, а перетинає цей ярус, а в усі інші комірки пам'яті, виділені для даного ярусу, записують число, яке не входить в множину номерів вершин, та виконанні даних дій до тих пір, доки не будуть переглянуті всі дуги графа, крім дуг останнього ярусу, в якому знаходяться вихідні дуги графа, для яких в комірку пам'яті ij записують номер вершини k, з якої виходить дана дуга j, а в усі інші комірки пам'яті, виділені для даного ярусу, записують число, яке не входить в множину номерів вершин, на етапі зчитування інформації здійснюють зчитуван , , ня вмісту комірок пам'яті ij(i  0, l  1 j  1 n) та, залежно від зчитаних значень, відображають вершину k та дугу j в i-му ярусі за правилом: якщо вмістом комірки ij є число, що входить до множини номерів вершин, то в i-му ярусі відображають вершину k, якщо вона не була відображена раніше, і дугу j, яка входить в цю вершину; якщо вмістом комірки ij є число, що входить до множини номерів вершин і вмістом комірки i+1,j є число, що входить до множини номерів вершин, або дорівнює 0, то в i-му ярусі відображають дугу з номером j, що виходить з даної вершини; якщо вміст комірки ij містить значення 0, то в i-му ярусі дугу з номером j продовжують до наступного ярусу (перетинає i-й ярус і не надходить в жодну вершину даного ярусу); та виконанні даних дій до тих пір, доки не буде зчитано вміст всіх комірок пам'яті та відображені всі дуги та вершини графа алгоритму. 7 Розглянемо реалізацію способу збереження в пам'яті потокового графа алгоритму у формі структурної матриці на прикладі потокового графа алгоритму, наведеного на фіг. 1. Спочатку виконаємо етап маркування графа алгоритму та етап запису інформації. Виконаємо нумерацію дуг, вершин та ярусів за описаним вище правилом. П'ять вершин нумеруються натуральними числами k  1,5 . Ці вершини розподіляють по чотирьох ярусах таким чином, що в i-му ярусі ( k  0,3) розміщені тільки вершини, на які надходять дуги від вершин попередніх ярусів і не надходять від вершин того ж ярусу та наступних ярусів. Нумерацію ярусів починаємо з ярусу, на якому виконуються операції над вхідними даними і закінчуємо ярусом, в якому знаходяться вихідні дуги графа. Кількість n вхідних дуг потокового графа алгоритму дорівнює шести. Нумерацію дуг розпочинаємо з першого ярусу, і кожній вхідній дузі даного ярусу привласнюємо натуральне число j( j  1,6) , а від нього вниз за правилом: вихідним дугам привласнюють довільне значення із множини натуральних чисел, що привласнені дугам, які входять в дану вершину (фіг. 1). Для кожного ярусу потокового графа алгоритму виділяється 6 комірок пам'яті, тому для збереження в пам'яті даного потокового графа алгоритму, який має 4 яруси, необхідно виділити 24 комірки. Переглядаємо дуги нульового ярусу: перша та друга дуги надходять в першу вершину, тому в комірки пам'яті 01 та 02 записують значення 1 (фіг. 2); третя та четверта дуги надходять в другу вершину, тому в комірки пам'яті 03 та 04 записують значення 2 (фіг. 3); відповідно в комірки пам'яті 05 та 06 записують значення 3. (фіг. 4). Переглянемо дуги першого ярусу: друга та третя дуги надходять в вершину з номером 4, тому в комірки пам'яті 12 та 13 записують значення 4; п'ята дуга не надходить в жодну з вершин, а перетинає цей ярус, тому в комірку 15 записують 0, а в усі інші комірки пам'яті, виділені для даного ярусу, записують число, яке не входить в множину номерів вершин, і в даному випадку дорівнює 6 (фіг. 5). На другому ярусі дуги із номерами 3 та 5 входять в вершину із номером 5, тому в комірки із номерами 23 та 25 записують число 5, а в усі інші комірки пам'яті, виділені для даного ярусу, записують число, яке не входить в множину номерів вершин, і в даному випадку дорівнює 6 (фіг. 6). Для збереження вихідної дуги останнього третього ярусу із номером 3, в комірку пам'яті 33 записують номер вершини 5, з якої виходить дана дуга, а в усі інші комірки пам'яті, виділені для даного ярусу, записують число, яке не входить в множину номерів вершин - число 6 (фіг. 7). Таким чином, здійснений перегляд всіх дуг кожного ярусу та записано в пам'яті потоковий граф алгоритму. Розглянемо етап зчитування інформації того ж потокового графа алгоритму. Кроки виконання етапу наведено на фіг. 8 - фіг. 10. Формування нульового ярусу потокового графа алгоритму (фіг. 8): 96041 8 - вмістом комірки 01 є число 1, що входить до множини номерів вершин, тому в 0-му ярусі відображаємо вершину 1, оскільки вона не була відображена раніше, і дугу 1, яка входить в цю вершину 1; - вмістом комірки 02 є також число 1, що входить до множини номерів вершин, і оскільки в 0-му ярусі вершина 1 відображена раніше, то відображаємо дугу 2, що входить в дану вершину 1; - вмістом комірки 02 є число 1, а вмістом комірки 12 є число 4, які входять до множини номерів вершин, тому відображаємо дугу з номером 2, що виходить з вершини 1; - вмістом комірки 03 є число 2, що входить до множини номерів вершин і, оскільки, вона не була відображена раніше, то в 0-му ярусі відображаємо вершину 2 і дугу 3, яка входить в цю вершину 2; - вмістом комірки 03 є число 2 та вмістом комірки 13 є число 4, які входять до множини номерів вершин, тому відображаємо дугу з номером 3, що виходить з вершини 2; - вмістом комірки 04 є число 2, що входить до множини номерів вершин, і оскільки в 0-му ярусі вершина 2 відображена раніше, то відображаємо дугу 4, що входить в вершину 2; - вмістом комірки 05 є число 3, що входить до множини номерів вершин і, оскільки, вона не була відображена раніше, то в 0-му ярусі відображаємо вершину 3 і дугу 5, яка входить в цю вершину 3; - вмістом комірки 05 є число 3, що входить до множини номерів вершин і вмістом комірки 15 є число 0, тому відображаємо дугу з номером 5, що виходить з вершини 3; - вмістом комірки 06 є також число 3, що входить до множини номерів вершин, і оскільки в 0-му ярусі вершина 3 відображена раніше, то відображаємо дугу 6, що входить в вершину 3. Формування першого ярусу потокового графа алгоритму (фіг. 9): - вмістом комірки 11 є число 6, що не входить до множини номерів вершин, тому нічого не відображаємо, а переходимо до наступної комірки; - вмістом комірки 12 є число 4, що входить до множини номерів вершин, і оскільки в 1-му ярусі вершина 4 не була відображена раніше, то відображаємо вершину 4 та дугу 2 продовжуємо з попереднього ярусу до вершини 4 поточного ярусу; - вмістом комірки 13 є число 4, що входить до множини номерів вершин і, оскільки, вершина 4 була відображена раніше, то в 1-му ярусі продовжуємо дугу 3 з попереднього ярусу до вершини 4; - вмістом комірки 13 є число 4 та вмістом комірки 23 є число 5, які входять до множини номерів вершин, тому відображаємо дугу з номером 3, що виходить з вершини 4; - вмістом комірки 14 є число 6, що не входить до множини номерів вершин, тому переходимо до наступної комірки; - вмістом комірки 15 є число 0, тому в 1-му ярусі дугу з номером 5 продовжують з попереднього ярусу до наступного ярусу (дуга з номером 5 перетинає 1-й ярус і не надходить в жодну вершину даного ярусу); 9 96041 - вмістом комірки 16 є число 6, що не входить до множини номерів вершин, тому переходимо до наступної комірки. Формування другого та третього ярусів потокового графа алгоритму (фіг. 10): - вмістом комірок 21 та 22 є число 6, що не входить до множини номерів вершин, тому переходимо до наступної комірки; - вмістом комірки 23 є число 5, що входить до множини номерів вершин, і оскільки в 2-му ярусі вершина 5 не була відображена раніше, то відображаємо вершину 5 та дугу 3 продовжуємо з попереднього ярусу до вершини 5; - вмістом комірки 23 є число 5 та вмістом комірки 33 є число 5, які входять до множини номерів вершин, тому відображаємо дугу з номером 3, що виходить з вершини 5; - вмістом комірки 24 є число 6, що не входить до множини номерів вершин, тому нічого не відображаємо, а переходимо до наступної комірки; - вмістом комірки 25 є число 5, що входить до множини номерів вершин, і оскільки в 2-му ярусі вершина 5 була відображена раніше, то дугу 5 продовжуємо до вершини 5; - вмістом комірки 26 є число 6, що не входить до множини номерів вершин, тому нічого не відображаємо. Таким чином, зчитано вміст всіх комірок пам'яті та відображено всі дуги та вершини потокового графа алгоритму. Кількість комірок пам'яті, необхідних для збереження графа алгоритму запропонованим способом, дорівнює добутку кількості ярусів на кількість дуг нульового ярусу - l  n , де l - кількість ярусів, a n - кількість дуг нульового ярусу. Оскільки, кількість ярусів l завжди менша за загальну кількість N вершин графа, а кількість дуг n нульового ярусу завжди менша за загальну кількість М дуг, то об'єм пам'яті, необхідний для збереження графа алгоритму запропонованим способом, завжди буде меншим ніж при використанні відомих способів збереження в пам'яті графа алгоритму, і в найгіршому випадку, коли N вершин графа розміщені по 1 ярусах і кожна вершина має тільки одну дугу: 10 - кількість комірок пам'яті Vi для збереження матриці інциденцій дорівнюватиме 2  l2 ; Vi  N  M  N - кількість комірок пам'яті Vc / c для збереження матриці суміжності та символьної матриці Vc / c  N  M  N 2  l 2 ; - кількість комірок пам'яті Vnew для збереження структурної матриці при використанні запропонованого способу Vnew  l  n ; а оскільки кожна вершина має тільки одну дугу (n  1) , то Vnew  l , що в l раз менше, ніж кількість комірок пам'яті для збереження матриці інциденцій, суміжності та символьної матриці. Зменшення кількості комірок пам'яті при використанні запропонованого способу збереження в пам'яті потокового графа алгоритму у формі структурної матриці в порівнянні із використанням відомих способів збереження в пам'яті графа алгоритму у формі матриці інциденцій, матриці суміжності та символьної матриці підтверджено експериментально і для графа алгоритму швидкого перетворення Фур'є (ШПФ) різної розмірності показані на фіг. 11 та наведені в таблиці 1. На фіг. 11 по осі X відкладено розмірність ШПФ, а по осі Y - кількість комірок пам'яті. Залежність кількості комірок пам'яті для збереження графа алгоритму ШПФ від його розмірності на фіг. 11 позначено: для матриці інциденцій переривчастою лінією з квадратом, для матриці суміжності - переривчастою лінією з колом, та для символьної матриці - суцільною лінією з трикутником. На фіг. 11 показано, що із збільшенням кількості точок алгоритму ШПФ кількість комірок пам'яті, необхідних для збереження графа алгоритму ШПФ за допомогою матриці інциденцій, суміжностей та символьної матриці експоненційно зростають, в той час як кількість комірок пам'яті, необхідних для збереження графа алгоритму ШПФ за допомогою структурної матриці, збільшується лінійно. Таблиця 1 Оцінка різних способів збереження в пам'яті графа алгоритму швидкого перетворення Фур'є Коефіцієнт зменшення Кількість комірок пам'яті для збереження гра- кількості комірок пам'яті Параметри графа алгоритму фа алгоритму запропонованого способу по відношенню запропонований суміжності, спосіб у вигляді К-ть до матриці вершин, дуг, ярусів, інициденцій, до матриц символьної структурної матвх. д суміжності, N М l інциденцій Vi(NM) n символьної Vc/c(NN) риці Vnew(l  n) 4 8 16 32 64 4 12 32 80 192 12 32 80 192 448 2 3 4 5 6 48 384 2560 15360 86016 16 144 1024 6400 36864 8 24 64 160 384 6 16 40 96 224 2 6 16 40 96 11 96041 12 Продовження таблиці 1 Коефіцієнт зменшення Кількість комірок пам'яті для збереження гра- кількості комірок пам'яті фа алгоритму запропонованого способу по відношенню запропонований суміжності, спосіб у вигляді до матриці вершин, дуг, ярусів, інициденцій, до матриц символьної структурної матсуміжності, N М l інциденцій Vi(NM) символьної Vc/c(NN) риці Vnew(l  n) 448 1024 7 458752 200704 896 512 224 1024 2304 8 2359296 1048576 2048 1152 512 2304 5120 9 11796480 5308416 4608 2560 1152 5120 11264 10 57671680 26214400 10240 5632 2560 11264 24576 11 276824064 126877696 22528 12288 5632 24576 53248 12 1308622848 603979776 49152 26624 12288 53248 114688 13 6106906624 2835349504 106496 57344 26624 Параметри графа алгоритму К-ть вх. д n 128 256 512 1024 2048 4096 8192 Вказаний результат зменшення кількості комірок пам'яті запропонованого способу по відношенню до відомих способів досягається тим, що в запропонованому способі збереження графа алгоритму кількість комірок залежить від кількості дуг одного (нульового) ярусу та загальної кількості ярусів, а не від загальної кількості вершин та/або дуг, що завжди менше кількості дуг або вершин потокового графа алгоритму. Таким чином, запропонований спосіб збереження в пам'яті потокового графа алгоритму у формі структурної матриці дозволяє зменшити об'єм пам'яті, необхідний для збереження графа алгоритму, та розширити функціональні можливості за рахунок забезпечення розподілу та закріплення вершин за ярусами графа алгоритму. Джерела інформації: 1. Оре О. Теория графов. - М.: Наука. 1980. С. 30. - 336с. 2. Миллер Р., Боксер Л. Последовательные и параллельные алгоритмы. - М.: БИНОМ. Лаборатория знаний, 2006. - С. 325-960с. 3. Е.Л. Рабкин, Ю.Б. Фарфоровская. Дискретная математика. Булевы функции и элементы теории графов. http://dvo.sut.ru/libr/himath/w163rabky/11.htm. 4. Ковалюк Т.В. Основи програмування. - К.: Видавнича група BHV, 2005. - С. 340-384с. 13 96041 14 15 96041 16 17 Комп’ютерна верстка М. Ломалова 96041 Підписне 18 Тираж 23 прим. Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601