Спосіб визначення параметрів нелінійної дисипативної коливальної системи
Формула / Реферат
Спосіб визначення параметрів коливань нелінійної дисипативної коливальної системи, по якому задають перше початкове і перше кінцеве значення амплітуди вільних затухаючих коливань нелінійної дисипативної коливальної системи, проводять вимір першого часового інтервалу і число циклів коливань в цьому часовому інтервалі при зміні амплітуди вільних затухаючих коливань від першого початкового до першого кінцевого значення, далі задають друге початкове і друге кінцеве значення амплітуди вільних затухаючих коливань і проводять вимір другого часового інтервалу і число циклів коливань в цьому часовому інтервалі при зміні амплітуди вільних затухаючих коливань від другого початкового до другого кінцевого значення, потім два рази змінюють інерційність нелінійної дисипативної коливальної системи і при кожній зміні інерційності проводять вищевказану сукупність операцій по визначенню першого і другого часових інтервалів і числа циклів коливань в цих часових інтервалах при зміні амплітуди вільних затухаючих коливань від її першого початкового значення до першого кінцевого значення, від другого початкового значення до другого кінцевого значення відповідно, який відрізняється тим, що додатково проводять "N-1" разів вимір першого часового інтервалу і число циклів коливань в кожному часовому інтервалі при зміні амплітуди вільних затухаючих коливань від першого початкового до першого кінцевого значення, "N-1" разів вимір другого часового інтервалу і число циклів коливань в кожному часовому інтервалі при зміні амплітуди вільних затухаючих коливань від другого початкового до другого кінцевого значення, при кожній зміні інерційності проводять "N-1" разів вимір першого часового інтервалу і число циклів коливань в кожному часовому інтервалі при зміні амплітуди вільних затухаючих коливань від першого початкового значення до першого кінцевого значення, "N-1" разів вимір другого часового інтервалу і число циклів коливань в кожному часовому інтервалі при зміні амплітуди вільних затухаючих коливань від другого початкового значення до другого кінцевого значення, при цьому оцінки частоти вільних коливань лінійної сильно дисипативної породжувальної коливальної системи і частоти вільних коливань лінійної консервативної породжувальної коливальної системи "![]() " та "
" та "![]() " відповідно, а також оцінки маси "
" відповідно, а також оцінки маси "![]() " коливальної системи, коефіцієнта "
" коливальної системи, коефіцієнта "![]() " жорсткості, коефіцієнта "
" жорсткості, коефіцієнта "![]() " демпфування, коефіцієнта "
" демпфування, коефіцієнта "![]() " опору визначають із наведених співвідношень:
" опору визначають із наведених співвідношень:
![]()
![]()
![]()
-
![]()
-
![]()
![]() ;
;
![]()
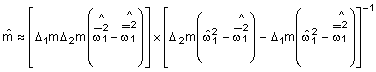 ,
,
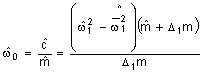 ,
, 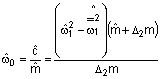 ;
;
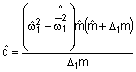 , або
, або 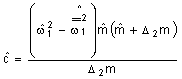 ,
,
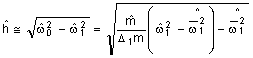 , або
, або 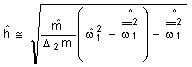 ,
,
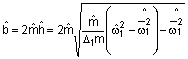 , або
, або 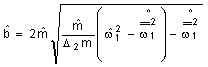 ,
,
де ![]() - оцінки значень параметрів
- оцінки значень параметрів ![]() відповідно;
відповідно; ![]() - оцінки значень частот
- оцінки значень частот ![]() ,
, ![]() - перша і друга додаткові маси;
- перша і друга додаткові маси; ![]() - перша і друга групи чисел циклів вільних затухаючих коливань дисипативної коливальної системи, маса якої "
- перша і друга групи чисел циклів вільних затухаючих коливань дисипативної коливальної системи, маса якої "![]() ", при зміні амплітуди вільних затухаючих коливань системи від першого початкового значення
", при зміні амплітуди вільних затухаючих коливань системи від першого початкового значення ![]() до першого кінцевого значення
до першого кінцевого значення ![]() , від другого початкового значення
, від другого початкового значення ![]() до другого кінцевого значення
до другого кінцевого значення ![]() відповідно;
відповідно; ![]() - перша і друга групи часових інтервалів, що відповідають групам чисел циклів
- перша і друга групи часових інтервалів, що відповідають групам чисел циклів ![]() циклів коливань коливальної системи;
циклів коливань коливальної системи; ![]() - третя і четверта групи чисел циклів вільних затухаючих коливань нелінійної дисипативної коливальної системи, маса якої
- третя і четверта групи чисел циклів вільних затухаючих коливань нелінійної дисипативної коливальної системи, маса якої ![]() , при зміні амплітуди затухаючих коливань від першого початкового значення
, при зміні амплітуди затухаючих коливань від першого початкового значення ![]() до першого кінцевого значення
до першого кінцевого значення ![]() , від другого початкового значення
, від другого початкового значення ![]() до другого кінцевого значення
до другого кінцевого значення ![]() відповідно;
відповідно; ![]() - третій і четвертий часові інтервали, що відповідають групам чисел
- третій і четвертий часові інтервали, що відповідають групам чисел ![]() циклів коливань коливальної системи;
циклів коливань коливальної системи; ![]() - п'ята і шоста групи чисел циклів вільних затухаючих коливань нелінійної дисипативної коливальної системи, маса якої
- п'ята і шоста групи чисел циклів вільних затухаючих коливань нелінійної дисипативної коливальної системи, маса якої ![]() , при зміні амплітуди коливань від першого початкового значення
, при зміні амплітуди коливань від першого початкового значення ![]() до першого кінцевого значення
до першого кінцевого значення ![]() , від другого початкового значення
, від другого початкового значення ![]() до другого кінцевого значення
до другого кінцевого значення ![]() відповідно;
відповідно; ![]() - п'ята і шоста групи часових інтервалів, що відповідають числам
- п'ята і шоста групи часових інтервалів, що відповідають числам ![]() циклів коливань коливальної системи.
циклів коливань коливальної системи.
Текст
Спосіб визначення параметрів коливань нелінійної дисипативної коливальної системи, по якому задають перше початкове і перше кінцеве значення амплітуди вільних затухаючих коливань нелінійної дисипативної коливальної системи, проводять вимір першого часового інтервалу і число циклів коливань в цьому часовому інтервалі при зміні амплітуди вільних затухаючих коливань від першого початкового до першого кінцевого значення, далі задають друге початкове і друге кінцеве значення амплітуди вільних затухаючих коливань і проводять вимір другого часового інтервалу і число циклів коливань в цьому часовому інтервалі при зміні амплітуди вільних затухаючих коливань від другого початкового до другого кінцевого значення, потім два рази змінюють інерційність нелінійної дисипативної коливальної системи і при кожній зміні інерційності проводять вищевказану сукупність операцій по визначенню першого і другого часових інтервалів і числа циклів коливань в цих часових інтервалах при зміні амплітуди вільних затухаючих коливань від її першого початкового значення до першого кінцевого значення, від другого початкового значення до другого кінцевого U 2 ; (19) 1 3 ˆ c ˆ m ˆ0 ˆ c ˆ m ˆ2 1 ^ 2 ˆ ˆ 1 mm ˆ c ˆ2 0 ˆ b де 2m ˆˆ 2mh ˆ 2m ˆ 2m ^ 2 1 ˆ m ˆ2 1 1m ^ 2 1 ^ 2 1 ˆ m ˆ2 1 2m ˆ ˆ ˆ ˆ m, c, ˆ 0, h, b ^ 2 1 , або m) - пер вань коливальної системи; n3i, n4i i 1 N - третя і , четверта групи чисел циклів вільних затухаючих коливань нелінійної дисипативної коливальної системи, маса якої m 1m , при зміні амплітуди затухаючих коливань від першого початкового значення Xa1 до першого кінцевого значення , 3it, 4it i 1 N - третій і четвертий часові інтервали, що відповідають групам чисел n3i, n4i циклів , коливань коливальної системи; n5i, n6i i 1 N п'ята і шоста групи чисел циклів вільних затухаючих коливань нелінійної дисипативної коливальної системи, маса якої m 2m , при зміні амплітуди ^ 2 1 , ˆ m ˆ2 1 1m 2m Xa2 , від другого початкового значення Xa3 до другого кінцевого значення Xa4 відповідно; , ˆ2 1 ˆ m ˆ2 m 1 2 ˆ h або , 2m m, вого значення Xa4 відповідно; 1it, 2it i 1 N , перша і друга групи часових інтервалів, що відповідають групам чисел циклів n1i, n2i циклів коли 1m ^ 2 ˆ ˆ 1 mm 1m гого початкового значення Xa3 до другого кінце; 1m ˆ2 1 ˆ b 2m 2m ˆ c ˆ h , ^ 2 ˆ 1 m 2m, ша і друга додаткові маси; n1i, n2i i 1 N - перша і , друга групи чисел циклів вільних затухаючих коливань дисипативної коливальної системи, маса якої ˆ " m ", при зміні амплітуди вільних затухаючих коливань системи від першого початкового значення Xa1 до першого кінцевого значення Xa2 , від дру 1m 1m ˆ2 1 4 1m, 2m( 1m ^ 2 ˆ 1 m ˆ2 1 ˆ0 52563 ^ 2 1 ^ 2 1 , коливань від першого початкового значення Xa1 до першого кінцевого значення Xa2 , від другого або , значення Xa4 відповідно; 5it, 6it i 1 N - п'ята і шоста групи часових інтервалів, що відповідають числам n5i, n6i циклів коливань коливальної системи. ^ 2 1 , оцінки значень ^ початкового значення Xa3 до другого кінцевого параметрів ^ m, c, 0 , h, b відповідно; ˆ 1, , 1 - оцінки значень 1 частот 1, 1, 1 , Корисна модель відноситься до області машинобудівної, авіаційної і ракетно-космічної техніки, а саме, до способів визначення параметрів вільних коливань нелінійних дисипативних коливальних систем із кінцевим числом ступенів вільності і може бути застосована, зокрема, при визначенні моментів інерції за допомогою механічних коливальних систем. Відомий спосіб визначення параметрів нелінійної дисипативної коливальної системи, за яким задають перше початкове і перше кінцеве значення амплітуди вільних коливань нелінійної коливальної системи, вимірюють перший і другий часові інтервали зміни амплітуди коливань, вимір першого часового інтервалу і числа циклів коливань в цьому часовому інтервалі проводять при зміні ам 5 плітуди вільних коливань від першого початкового значення до першого кінцевого значення амплітуди, потім задають друге початкове і друге кінцеве значення амплітуди вільних коливань, вимір другого часового інтервалу і числа циклів коливань в цьому часовому інтервалі проводять при зміні амплітуди вільних коливань від її другого початкового значення до другого кінцевого значення, після чого змінюють інерційність нелінійної дисипативної коливальної системи і проводять вищевказану сукупність операцій по виміру першого і другого часових інтервалів і чисел циклів в кожному часовому інтервалі при зміні амплітуди вільних коливань від її першого початкового значення до першого кінцевого значення, від другого початкового значення до другого кінцевого значення відповідно, а визначення параметра нелінійної дисипативної коливальної системи проводять при урахування часових інтервалів і чисел циклів вільних коливань (див. ав. Св.. СРСР № 1703990, МПК G01H 1/00, 1992). Недоліком відомого способу є обмежені функціональні можливості цієї системи, що пояснюється визначенням тільки одного параметра коливань слабко дисипативної нелінійної коливальної системи, що, в свою чергу, приводить до неможливості визначення множини параметрів сильно дисипативної нелінійної коливальної системи. За прототип вибрано спосіб визначення параметрів нелінійної дисипативної коливальної системи, за яким задають перше початкове і перше кінцеве значення амплітуди затухаючих коливань нелінійної дисипативної коливальної системи, проводять вимір першого часового інтервалу і числа циклів коливань в цьому часовому інтервалі при зміні амплітуди затухаючих коливань від першого початкового значення до першого кінцевого значення, потім задають друге початкове і друге кінцеве значення амплітуди затухаючих коливань, проводять вимір другого часового інтервалу і числа циклів коливань в цьому часовому інтервалі при зміні амплітуди затухаючих коливань від її другого початкового значення до другого кінцевого значення, після чого один раз змінюють інерційність нелінійної дисипативної коливальної системи і приводять вищевказану сукупність операцій по визначенню першого і другого часових інтервалів і числа циклів в кожному часовому інтервалі при зміні амплітуди коливань від її першого початкового значення до першого кінцевого значення, від другого початкового значення до другого кінцевого значення відповідно, далі додатково другий раз змінюють інерційність нелінійної дисипативної коливальної системи і проводять вищевказану сукупність операцій по визначенню першого і другого часових інтервалів і чисел циклів коливань в цих часових інтервалах при зміні амплітуди вільних коливань від її першого початкового значення до першого кінцевого значення, від другого початкового значення до другого кінцевого значення відповідно, при цьому частоти вільних коливань лінійної дисипативної породжувальної системи і вільних коливань лінійної консервативної породжувальної системи, а також масу коливальної системи, коефіцієнт жорсткості, коефіцієнти демпфування та опору визначають по відповідних 52563 6 співвідношеннях (див. патент України на корисну модель № 45033, МПК G01H11/00, 26.10.2009). Згідно цього способу можливо визначати параметри сильно дисипативної нелінійної коливальної системи, але при цьому має місце недостатня точність їх визначення, що пояснюється неврахуванням випадкових похибок виміру, фіксації та запам'ятовування інформаційних масивів часових інтервалів та чисел циклів (періодів) коливального процесу при зміні амплітудних значень коливань, а також недостатнім по множині інформаційним масивам даних для зменшення похибок визначення параметрів шляхом усереднення. В основу корисної моделі поставлене завдання удосконалення способу визначення параметрів нелінійної сильно дисипативної коливальної системи шляхом підвищення точності визначення параметрів лінійної дисипативної породжувальної коливальної системи за рахунок проведення додаткових технічних операцій по вимірюванню і реєстрації інформаційних масивів часових інтервалів і чисел циклів коливальних процесів, які формують розширений інформаційний масив, що дає підстави для формування нового алгоритму математичних перетворень, які приводять до зменшення впливу випадкових похибок вимірювання на результат визначення параметрів при реалізації вільних коливань лінійної дисипативної породжувальної коливальної системи. Поставлене завдання вирішується тим, що в способі визначення параметрів нелінійної дисипативної коливальної системи, по якому задають перше початкове і перше кінцеве значення амплітуди вільних затухаючих коливань нелінійної дисипативної коливальної системи, проводять вимір першого часового інтервалу і число циклів коливань в цьому часовому інтервалі при зміні амплітуди вільних затухаючих коливань від першого початкового до першого кінцевого значення, далі задають друге початкове і друге кінцеве значення амплітуди вільних затухаючих коливань і проводять вимір другого часового інтервалу і число циклів коливань в цьому часовому інтервалі при зміні амплітуди вільних затухаючих коливань від другого початкового до другого кінцевого значення, потім два рази змінюють інерційність нелінійної дисипативної коливальної системи і при кожній зміні інерційності проводять вищевказану сукупність операцій по визначенню першого і другого часових інтервалів і числа циклів коливань в цих часових інтервалах при зміні амплітуди вільних затухаючих коливань від її першого початкового значення до першого кінцевого значення, від другого початкового значення до другого кінцевого значення відповідно, згідно із корисною моделлю, додатково проводять «N-1» разів вимір першого часового інтервалу і число циклів коливань в кожному часовому інтервалі при зміні амплітуди вільних затухаючих коливань від першого початкового до першого кінцевого значення, «N-1» разів вимір другого часового інтервалу і число циклів коливань в кожному часовому інтервалі при зміні амплітуди вільних затухаючих коливань від другого початкового до другого кінцевого значення, при кожній зміні інерційності проводять «N-1» разів вимір першого 7 52563 часового інтервалу і число циклів коливань в кожному часовому інтервалі при зміні амплітуди вільних затухаючих коливань від першого початкового значення до першого кінцевого значення, «N-1» разів вимір другого часового інтервалу і число циклів коливань в кожному часовому інтервалі при зміні амплітуди вільних затухаючих коливань від другого початкового значення до другого кінцевого значення, при цьому оцінки частоти вільних коливань лінійної сильно дисипативної породжувальної 1it ˆ1 2 3it ^ 2 ˆ 1 m ˆ c ˆ m ^ 2 ˆ 1 m 4it ˆ b ^ 2 1 ˆˆ 2mh 2 t 4i 3it 1 ^ 2 1 2 1m ˆ 1 ˆ 2m ; ˆ m ˆ2 m 1 1 , ^ 2 1 ^ 2 1 , або ˆ b ^ 2 ˆ ˆ 1 mm ˆ m 2m , або ^ 2 1 , ^ m, c, 0 , h, b відповідно; ˆ 1, , 1 - оцінка значень 1 частот 1, 1, 1 ; 1m, 2m( 1m 2m, 2m ˆ m m 1 ˆ2 1 ˆ2 1 ^ 1m 2m ˆ2 1 ^ 2 1 ˆ ˆ ˆ ˆ де m, c, ˆ 0, h, b - оцінки значень параметрів , ˆ c ˆ 2m ˆ m 2m ; 1m ˆ2 0 1it 2it 2 2m ˆ 1 2 t 4i n3i 3it 2t 1 i ^ 2 1 2it 3it 2it 3it 2m ^ 2 ˆ ˆ 1 mm ˆ c ˆ h n1i 1it m 1 2m ˆ2 1 ˆ h 2t 1 i n4i 4it m 1 ˆ c ˆ m ˆ2 1 4it , ˆ2 1 ˆ0 ˆ цієнта " b " опору визначають із наведених співвідношень: 4it 2t 3i ^ 2 1m 2m 1 ˆ m ˆ0 2t 4i 2t 2i 1t i ˆ2 1 2t 3i 2it коливальної системи і частоти вільних коливань лінійної консервативної породжувальної коливальної системи " 1" та " 0" відповідно, а також оцінˆ ˆ ки маси " m " коливальної системи, коефіцієнта " c " ˆ " демпфування, коефіжорсткості, коефіцієнта " h n2i 2it 2t 2i 1t i 8 ^ 2 1 ˆ2 1 ^ 2 1 ^ 2 1 , ^ 2 1 , або 1m m, 2m m) - пер , ша і друга додаткові маси; n1i, n2i i 1 N - перша і друга групи чисел циклів вільних затухаючих коливань дисипативної коливальної системи, маса якої ˆ " m ", при зміні амплітуди вільних затухаючих коливань системи від першого початкового значення Xa1 до першого кінцевого значення Xa2 , від другого початкового значення Xa3 до другого кінце , вого значення Xa4 відповідно; 1it, 2it i 1 N перша і друга групи часових інтервалів, що відповідають групам чисел n1i, n2i циклів коливань ко, ливальної системи; n3i, n4i i 1 N - третя і четверта групи чисел циклів вільних затухаючих коливань нелінійної дисипативної коливальної системи, маса якої m 1m , при зміні амплітуди 9 затухаючих коливань від першого початкового значення Xa1 до першого кінцевого значення Xa2 , від другого початкового значення Xa3 до другого кінцевого значення Xa4 відповідно; , 3it, 4it i 1 N - третій і четвертий часові інтервали, що відповідають групам чисел n3i, n4i циклів , коливань коливальної системи; n5i, n6i i 1 N п'ята і шоста групи чисел циклів вільних затухаючих коливань нелінійної дисипативної коливальної системи, маса якої m 2m , при зміні амплітуди коливань від першого початкового значення Xa1 до першого кінцевого значення Xa2 , від другого початкового значення Xa3 до другого кінцевого , значення Xa4 відповідно; 5it, 6it i 1 N - п'ята і шоста групи часових інтервалів, що відповідають числам n5i, n6i циклів коливань коливальної системи. Застосування запропонованого способу визначення параметрів нелінійної сильно дисипативної коливальної системи разом з усіма суттєвими ознаками, включаючи відмінні, забезпечує формування розширеного інформаційного масиву, що дає підстави для формування нового алгоритму математичних перетворень, які приводять до зменшення впливу випадкових похибок вимірювання на результат визначення параметрів при реалізації вільних коливань лінійної дисипативної породжувальної коливальної системи. Формування нового способу і алгоритму для його забезпечення базується на наступних теоретичних дослідженнях. В роботі (Боголюбов Н.Н., Митропольский Ю.А. Асимптотические методы в теории нелинейных колебаний. - М.: Физматгиз, 1963. - С. 185) застосовано асимптотичний метод КриловаБоголюбова - Митропольского (КБМ) для отримання рішення диференціального рівняння, зокрема, другого порядку: d2 x dx 2x f x, , (1) 0 2 dt dt де: 0 - частота вільних коливань лінійної породжувальної коливальної системи; x - узагальнена координата; dx - нелінійна функція; f x, dt 0 - малий позитивний параметр. Рішення x Xa cos рівняння (1) в першому наближенні визначаються із рівнянь першого наближення (Боголюбов Н.Н., Митропольский Ю.А. Асимптотические методы в теории нелинейных колебаний. - М.: Физматгиз, 1963.-С. 185) dXa A1 Xa , dt (2) d 0 B1 Xa , dt де 52563 10 A1 Xa B1 Xa 1 2 f Xa cos , Xa 0 sin sin d , 0 0 (3) 2 1 f Xa cos , Xa 0 sin cos d , 2 Xa 0 0 2 Із системи рівнянь (2) першого наближення робиться висновок про можливість дослідження, аналізу і розрахунку повільно затухаючих або повільно зростаючих нелінійних коливань перехідних процесів, що наближені до гармонійних x=Xacos 0t, амплітуда Ха і частота 0 яких повільно змінюються. При проведенні досліджень, аналізу і розрахунку ряду динамічних систем мають місце випадки, коли коливні процеси відносяться до класу таких, що мають значне демпфування, або таких, що значно розходяться (Попов Е.П., Пальтов М.П. Приближенные методы исследования нелинейных автоматических систем. - М.: Физматгиз, 1960. - С. 507-512) x(t)=Xaexp( 0t)cos 0t, (4) але з таким показником затухання 0 і власною частотою 0, що повільно змінюються на визначеному обмеженому часовому інтервалі (Попов Е.П., Пальтов М.П. Приближенные методы исследования нелинейных автоматических систем. - М.: Физматгиз, 1960. - С. 507-512). Рішення (4) відповідає диференціальному рівнянню другого порядку (Попов Е.П., Пальтов М.П. Приближенные методы исследования нелинейных автоматических систем. - М.: Физматгиз, 1960. - С. 507-512) d2x dx 2x 0 , 2h (5) 0 2 dt dt 2 Cm 1, 2 2 h2 . 0 0 1 На підставі однорідного диференціального рівняння (5) диференціальне рівняння для нелінійної дисипативної коливальної системи має вигляд: d2x dx dx 2x 2h f x, . (6) 0 dt dt dt 2 де h 0, Узагальнення асимптотичного методу КБМ для рівняння (6) приводить до такої системи рівнянь першого наближення (Попов Е.П., Пальтов М.П. Приближенные методы исследования нелинейных автоматических систем. -М.: Физматгиз, 1960. - С. 507-512) dXa hX a 1 1 Xa , dt (7) d 1 B1 Xa , dt рішення яких має вигляд (8) x=Xasin . Для спрощення аналізу системи (7) вводять нову зміну y(t), причому Ya=Xa exp(ht), де Ya - амплітудне значення змінної y(t). Після введення нової змінної у(t) рівняння (7) першого наближення приймають вигляд * dXa (9) A1 Xa , dt 11 52563 d 1 B1 Xa , dt де * Xa Xa exp ht , (10) * dXa dXa hX a exp ht . dt dt Таким чином, системи рівнянь (2) і (9) аналогічні за винятком того, що Ха в системі (2) заміняють * на Xa Xa exp ht в системі (9). Проведемо нескладні перетворення співвідношень (9), (10) і отримаємо два таких рівняння першого наближення dXa hX a A1 Xa e ht , dt (11) d 1 B1 Xa . dt Із рівнянь (11) першого наближення отримаємо одне рівняння шляхом виключення малого позитивного множника d 1dt B X B X eht 1 a dXa hX aeht 1 a dt . (12) A1 Xa A1 Xa Беручи до уваги співвідношення =2 n, n - число циклів коливань, на підставі рівняння (12) отримаємо інтегральне співвідношення Xak tk B X B X 2 n 1 t eht 1 a dXa hX aeht 1 a dt ,(13) A1 Xa A1 Xa Xan tn де Xak , Xan - початкове і кінцеве значення амплітуд коливань; tn, tk - початкове і кінцеве значення часового інтервалу, що відповідає значенням амплітуд Xn, Xk. На підставі співвідношення (13) отримаємо систему рівнянь: X a2 2 n1 1 1t B X eht 1 a dXa A1 Xa Xa1 Xa4 2 n2 1 2t 2 n3 1 3t t2 B X hX aeht 1 a dt , A1 Xa t1 B X eht 1 a dXa A1 Xa X a3 t4 B X hX aeht 1 a dt ,(15) A1 Xa t3 X a2 2 n5 1 5t t8 Xa 2 1 4t t6 Xa4 2 n4 (14) t10 B X eht 1 a dXa A1 Xa Xa1 B X eht 1 a dXa A1 Xa X a3 B X eht 1 a dXa A1 Xa Xa1 B X hX aeht 1 a dt , (16) A1 Xa t5 B X hX aeht 1 a dt , (17) A1 Xa t7 B X hX aeht 1 a dt , (18) A1 Xa t9 N S1 2 n1i i 1 ˆ 1 1it Xa 2 Xa1 12 X a4 2 n6 1 6t t12 B X , hX aeht 1 a dt A1 Xa t11 B X eht 1 a dXa A1 Xa X a3 (19) де 1 cm 1 h2 , 1 cm 1 h2 , , 1m 1 cm 1 h2 2m (20) m, 2m m) 1m, 2 m( 1m 2m, 1m перша і друга додаткові маси; n1, n2 - числа циклів затухаючих коливань від першого початкового значення Xa1 до першого кінцевого значення Xa2 , від другого початкового значення Xa3 до другого кінцевого значення Xa4 відповідно; 1t, 2t - часові інтервали, що відповідають числам циклів n1, n2 ; n3 , n 4 - числа циклів затухаючих коливань маси 1m при зміні амплітуди затухаючих коливань від першого початкового значення Xa1 m до першого кінцевого значення Xa2 , від другого початкового значення Xa3 до другого кінцевого значення Xa4 відповідно; 3 t, 4 t - часові інтервали, що відповідають числам n3 , n4 циклів (періодів) коливань; n5 , n6 - числа циклів (періодів) затухаючих коливань маси m 2m при зміні амплітуди коливань від першого початкового значення Xa1 до першого кінцевого значення Xa2 , від другого початкового значення Xa3 до другого кінцевого значення Xa4 відповідно; 5 t, 6 t - часові інтервали, що відповідають числам n5 , n6 циклів коливань. При проведенні вимірювань групи часових інтервалів t, 2it, 3it, 4it, 5it, 6it , групи 1i n1i, n2i, n3i, n4i, n5i, n6i чисел циклів коливань, що відповідають фіксованим часовим інтервалам, а також амплітудні значення вільних затухаючих коливань вимірюють при наявності випадкових похибок. Тому на підставі системи рівнянь (14)-(19) отримаємо такі мінімізуючі фунціонали: B X exp ht 1 a dXa A1 Xa t2 t1 2 B X hX a exp ht 1 a dt A1 Xa . (21) 13 52563 N S2 2 n2i ˆ 1 2it Xa 4 i 1 Xa 3 N Xa 2 S3 2 n3i 1 3it i 1 Xa1 N Xa 4 S4 2 n4i 1 4it i 1 Xa 3 N Xa 2 S5 2 n5i 1 5it i 1 Xa1 N Xa 4 S6 2 n6i 1 6it i 1 Xa 3 B X exp ht 1 a dXa A1 Xa B X exp ht 1 a dXa A1 Xa B X exp ht 1 a dXa A1 Xa B X exp ht 1 a dXa A1 Xa B X exp ht 1 a dXa A1 Xa де ˆ 1 , 1 , 1 - оцінки частот 14 t4 t3 2 B X hX a exp ht 1 a dt A1 Xa t6 t5 t8 t7 1, 1, 1 відповід 6N -число експериментів. N 2t 3t 1i 1i i 1 i 1 N N 2t 1 1it 3i i 1 i 1 , (23) , (24) , (25) , (26) 2 B X hX a exp ht 1 a dt A1 Xa 2 B X hX a exp ht 1 a dt A1 Xa 2 t10 B X hX a exp ht 1 a dt A1 Xa t9 2 t12 t11 B X hX a exp ht 1 a dt A1 Xa ˆ 1 , 1 , 1 частот N (22) Після формування частинних похідних S1 S2 S1 S2 S1 S2 отримаємо , , , , , ˆ1 ˆ1 1 1 1 1 систему нормальних рівнянь відносно оцінок но; ˆ , 1, 1, 1 відповідно: N N N N n1i 1it n3i 3it 3it 1it ; i 1 i 1 i 1 i 1 2 N N 2t ˆ1 4it 2i i 1 i 1 N N 2t 1 2it 4i i 1 i 1 2 N N 2t ˆ1 5it 1i i 1 i 1 N N 2t 1 1it 5i i 1 i 1 2 N N 2t ˆ1 6it 2i i 1 i 1 N N 2t 1 2it 6i i 1 i 1 2 N N N n2i 2it n4i 4it 4it 2it ; i 1 i 1 i 1 i 1 (27) N N N N n1i 1it n5i 5it 5it 1it ; i 1 i 1 i 1 i 1 (28) N N N N n2i 2it n6i 6it 6it 2it ; i 1 i 1 i 1 i 1 (29) N (30) Із системи рівнянь (27) - (30) отримаємо аналітичні співвідношення для визначення оцінок ˆ 1 , 1 , 1 частот ˆ1 1, 1, 1 відповідно: 1it 2 3it 1t i 2t 2i 2t 3i 2it 1t i 2t 4i 2t 2i 2t 3i n2i 2it 4it n1i 1it 4it 4it 2t 1 i 3it 2t 1 i n4i 4it 2it 3it n3i 3it 2it 3it 2it 2t 4i 1it 2 t 4i ; (31) 15 52563 2t 1i 1 2 2t 2i 1t i 3it 2t 3i 2t 2i 2t 2i 1t i 2t 1i 1 2 1it 2t 2i 2t 2i 1it 2t 2i n2i 2it 4it 4it 16 4it n4i 4it 2t 1 i 2it 5it n1i 1it 3it 2t 1 i 2it 6it n6i 6it n2i 2it 2t 5i 6it 6it n1i 1it 2t 5i 6it n3i 3it 2t 1i 2it 5it На підставі (20) і застосовуючи співвідношення (31), (32), (33), отримаємо аналітичні співвідноˆ ˆ ˆ ˆ шення для визначення оцінок m, c, h, b параметрів ˆ m 2m ˆ2 1 ˆ c 2 1 2 1 ^ 2 ˆ ˆ 1 mm 1m 2 1 2t 6i 5it ; (33) ^ 2 ˆ 1 m m 1 (37) , m 1 ˆ2 1 ^ 2 ˆ 1 m 2m (38) ˆ c ˆ m 2m Аналітичні співвідношення для визначення ˆ ˆ оцінок b, h параметрів b,h відповідно отримаємо ^ 2 1 , (34) на підставі співвідношень (20), (31), (32), (33), (34), (37), (38): ˆ h ˆ2 0 ˆ m m 1 ˆ2 1 ˆ2 1 ^ 2 1 ^ 2 1 (39) або 1m (35) ˆ m 2m ˆ h або ^ 2 ˆ ˆ 1 mm 1it або ˆ0 1m ˆ2 1 2t 6i ˆ c ˆ m ˆ0 ; (32) 2it 5it 2it (20) і при виконанні умови h h h отримаємо наближені аналітичні співвідношення для визнаˆ ˆ чення оцінок m, c параметрів m, с ^ 2 1 2 t 4i 3it ˆ2 1 m,c,h,b відповідно математичної моделі нелінійної дисипативної коливальної системи. Після проведення нескладних перетворень ^ 2 1m 2m 1 1it n5i 5it 2t 1i 2 t 4i 3it 4it 2t 3i 2it 2m (36) ˆ c , 2m ˆ де оцінка m параметра «m» визначається співвідношенням (34), а оцінки ˆ 1 , 1 , 1 значень частот 1, 1, 1 визначається співвідношеннями (31), (32), (33) відповідно. Співвідношення для визначення оцінки ˆ 0 параметра 0 отримаємо на підставі (34), (35), (36) ˆ b ˆˆ 2mh ˆ 2m ˆ2 1 ^ 2 1 ˆ m ˆ2 m 1 1 ^ 2 1 ; ^ 2 1 (40) ^ 2 1 , (41) ^ 2 1 . (42) або ˆ b ˆ 2m ˆ m m 1 ˆ2 1 ^ 2 1 Отримані аналітичні співвідношення (31), (32), (33), (34), (35), (35), (37), (38), (39), (40), (41), (42) можуть знайти застосування для визначення інерційно - жорсткісних і дисипативних параметрів нелінійних сильно дисипативних коливальних систем, коливальні процеси в яких відносяться до 17 класу швидко затухаючих або швидкозростаючих із повільно змінювальним коефіцієнтом демпфування (опору) і частотою вільних коливань на обмеженому часовому інтервалі, математична модель яких відповідає лінійному однорідному диференціальному рівнянню другого порядку, а асимптотичні рішення визначають для відповідного нелінійного диференціального рівняння із швидко затухаючими або швидкозростаючими нелінійними коливаннями із кінцевим значенням коефіцієнта затухання. Спосіб визначення параметрів нелінійної сильно дисипативної коливальної системи реалізують на підставі наступного алгоритму: 1) формують N режимів вільних коливань досліджувальної нелінійної сильно дисипативної коливальної системи. Задають значення першої початкової Ха1 і першої кінцевої Ха2 амплітуд вільних затухаючих коливань цієї нелінійної системи; 2) при фіксації зміни амплітуди вільних затухаючих коливань від першого початкового Ха1 до першого кінцевого значення Ха2 реєструють і запам'ятовують значення першого часового інтервалу 1іt і число n1i i 1, N циклів коливань в часо вому інтервалі 1іt при повторенні N разів i 1, N такого алгоритму; 3) задають значення другої початкової Ха3 і другої кінцевої Ха4 амплітуд вільних коливань цієї системи; при фіксації зміни амплітуди вільних затухаючих коливань від другого початкового значення Ха3 до другого кінцевого значення Ха4 амплітуди вільних затухаючих коливань реєструють і запам'ятовують значення другого часового інтервалу 2іt і число n2і циклів коливань в цьому часовому інтервалі 2іt при повторенні N разів i 1, N такого алгоритму; 4) змінюють інерційність нелінійної дисипативної коливальної системи шляхом жорсткого з'єднання з масою "m" системи першої додаткової маси 1m при такій умові вибору маси 1m
ДивитисяДодаткова інформація
Назва патенту англійськоюMethod for determination of parameters of non-linear dissipative oscillatory system
Автори англійськоюPuz'ko Ihor Danylovych
Назва патенту російськоюСпособ определения параметров нелинейной диссипативной колебательной системы
Автори російськоюПузько Игорь Данилович
МПК / Мітки
МПК: G01H 11/00
Мітки: нелінійної, системі, параметрів, дисипативної, визначення, спосіб, коливальної
Код посилання
<a href="https://ua.patents.su/10-52563-sposib-viznachennya-parametriv-nelinijjno-disipativno-kolivalno-sistemi.html" target="_blank" rel="follow" title="База патентів України">Спосіб визначення параметрів нелінійної дисипативної коливальної системи</a>
Попередній патент: Креслярський пристрій для відтворення гіперболи
Наступний патент: Пристрій для статико-імпульсної обробки внутрішніх напівсферичних поверхонь
Випадковий патент: Застосування гетерометалічного комплексу [cu(en)2][mn2(c2o4)3].6h2o (en - етилендіамін) як прекурсора для одержання електрокаталізатора відновлення кисню












