Спосіб комплексної обробки навігаційної інформації від датчиків курсо-швидкісної навігаційної системи і супутникової навігаційної системи літального апарата

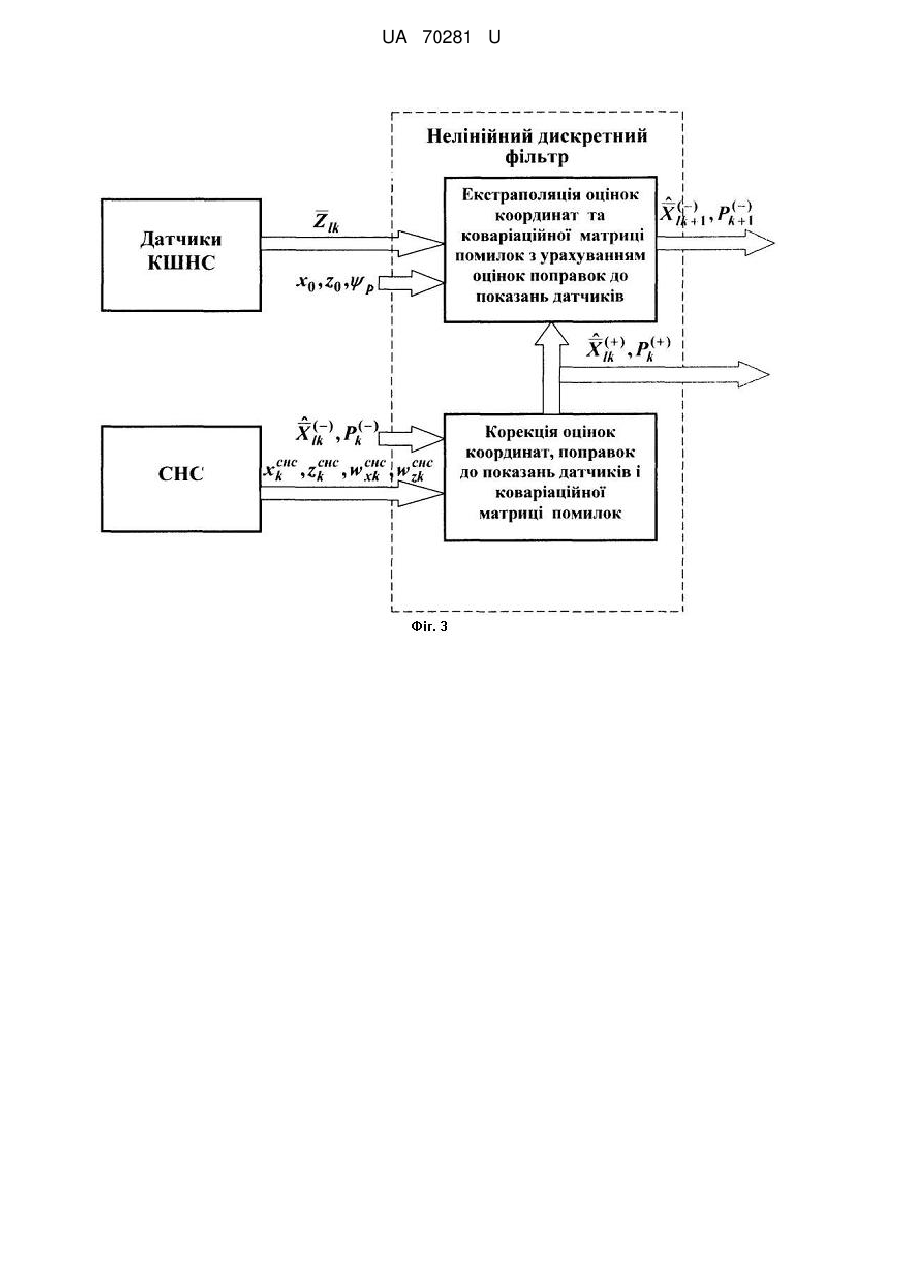
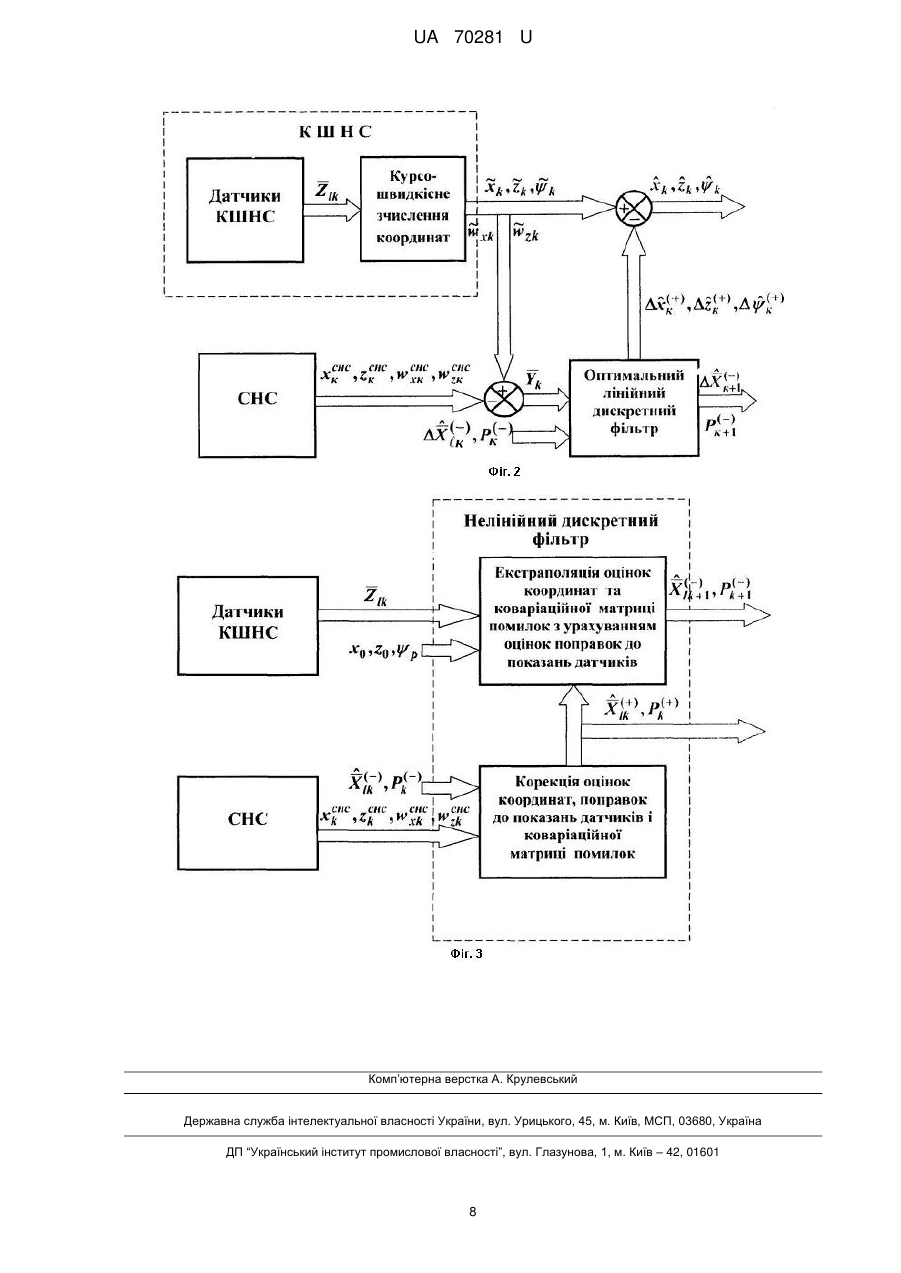
Реферат: Спосіб комплексної обробки навігаційної інформації від датчиків курсо-швидкісної навігаційної системи і супутникової навігаційної системи літального апарата включає зчислення поточних координат місцеположення центру мас літального апарата у вибраній системі координат (частковоортодромічній, геоцентричній, географічній та ін.) за інформацією від датчиків курсошвидкісної навігаційної системи, а також корекцію зчисленних координат за інформацією від супутникової навігаційної системи. Оцінки поточних координат місцеположення центра мас літального апарата і поправок до показань датчиків курсо-швидкісної системи на кожному кроці обробки навігаційної інформації одержують за допомогою дискретного нелінійного фільтра, в якому операцію оцінювання координат місцеположення, поправок до показань датчиків і коваріаційної матриці помилок оцінок реалізують після одержання поточної позиційношвидкісної інформації від супутникової навігаційної системи, а операцію екстраполяції оцінок координат місцеположення центра мас літального апарата виконують за допомогою формул курсо-швидкісного зчислення координат з використанням поточної інформації від датчиків з урахуванням оцінок поправок до показань цих датчиків. UA 70281 U (12) UA 70281 U UA 70281 U 5 10 15 Корисна модель належить до галузі навігації літальних апаратів, у якій курсо-швидкісні системи, зокрема системи курсо-повітряного і курсо-допплерівського типів, знаходять широке застосування [1]. Курсо-швидкісні навігаційні системи призначені для безперервного вимірювання і інтегрування в часі складових вектора шляхової швидкості літального апарата для отримання поточних координат місцеположення його центра мас щодо навігаційної системи відліку. Як опорні навігаційні системи координат для курсо-швидкісних навігаційних систем знаходять застосування геоцентрична, географічна і частковоортодромічна (плоска прямокутна) системи координат [1, 2, 4]. Для літальних апаратів малого і середнього радіусів дії зазвичай використовують частковоортодромічну систему координат OXYZ, горизонтальна вісь ОХ якої орієнтована під кутом p (кутом карти) до північного напряму меридіана, що проходить через початок координат О, а вісь OZ також лежить у горизонтальній площині і утворює праву прямокутну систему відліку. При нехтуванні кутами атаки , ковзання  і тангажу  в основу процедури курсо-повітряного зчислення частковоортодромічних координат приймають трикутник швидкостей, зображений на фіг. 1, та наступні відомі формули [1]:   t    Xt   X0   Vв cos    p  Ucos в   p dt 0 ; t      Zt   Z 0   Vв sin    p  Usin в   p dt (1) 0 , 20 25 де Х0, Z0 - початкові значення координат; Vв() - дійсна повітряна швидкість, вимірювана датчиком повітряної швидкості (далі передбачається, що всі вимірювання позиційно-швидкісних параметрів приводяться до центра мас об’єкта); () - кут курсу (кут між північним напрямом ON в площині опорного меридіана і проекцією подовжньої осі літального апарата на горизонтальну площину XOZ), вимірюваний датчиком курсу; U(), в(t)- горизонтальна складова швидкості вітру і кут напряму вітру (кут між напрямом на північ ON і проекцією швидкості вітру на площину OXZ), що задаються за допомогою датчика вітру. Співвідношенням (1) відповідають наступні формули зчислення координат ~ ~ ~ ~ X  Х  V cos     U cos    Т к 1 к Z к 1  Z к  ~  V вк   к р   к   вк р   ~ ~ ~ к=0, 1, вк sin  к   р  Uк sin  вк   р Т (2) …; 30 35 де ΔT - крок дискретності часу (крок інтегрування); ~ Vвк - результати вимірювання дійсної повітряної швидкості у момент часу t=t к; ~ ~ U к і вк - оцінки швидкості і кута напряму горизонтальної складової вітру, що задаються за допомогою датчика вітру; ~  к - результат вимірювання кута курсу датчиком курсу у момент t=tк. У першому наближенні справедливі співвідношення вигляду: ~ Vвк  Vвк  вк ; ~ Uк  Uк  U  Uк ; ~ вк  вк  в  вк(3) ; ~ к  к    к , де Vвк, вк - фактичні значення дійсної повітряної швидкості і кута курсу у момент t=t к; Uк, вк - фактичні значення горизонтальної складової швидкості вітру і кута напряму вітру; ΔU, Δв - систематичні помилки задання горизонтальної швидкості і кута вітру; Δ - систематична помилка датчика курсу; 1 UA 70281 U ηвк, ηUк, ημвк, ηк - випадкові помилки (типу дискретного «білого» шуму) з нульовими 2 2 середніми значеннями і відомими дисперсіями  2 ,  U ,  в ,  2 .  Vв Для побудови процедури курсо-повітряного обчислення геоцентричних і географічних координат літального апарата використовують наступні відомі формули [1]: t 1 Vв cos   Ucos в dt ; (4) Rh 0 ' t   '0   5 Vв sin   Usin в  d R  hcos ' 0 (5) t t    0   ; e2 sin 2' t  , 2 де: ' і  - геоцентрична і географічна широта; 2 e - квадрат ексцентриситету земного еліпсоїда, прийнятого для навігації; R - радіус Землі; h - висота польоту, яка може бути заміряна за допомогою баровисотоміра; Vв(t) і U(t) - горизонтальні проекції дійсної повітряної швидкості і швидкості вітру; в(t) - кут напряму горизонтального вітру; '0, 0 - початкові значення координат. Відповідно, в основу процедури курсо-допплерівського зчислення частковоортодромічних координат центра мас літального апарата приймаються наступні формули: t   ' t   10  t  Xt   X0   W cos    p   c  dt 0 ;  t  Zt   Z 0   W sin    p   c  dt (6) 0 , 15 20 де: W(), c() - вимірювані допплерівським вимірником шляхової швидкості і кута зносу горизонтальна складова шляхової швидкості і кут зносу (кут між проекціями шляхової швидкості і подовжньої осі літального апарата на площину OXZ); Х0, Z0 - початкові значення координат центра мас; (() - вимірюване датчиком курсу поточне значення кута курсу. Співвідношенням (6) відповідають наступні формули курсо-допплерівського зчислення частковоортодромічних координат центра мас літального апарата: ~ ~ ~ X  Х  W cos      Т к 1 к Z к 1  Z к   ~ ~  W sin к к к к р cк   ~   р   cк Т , к=0, 1, 2, (7) …, 25 30 ~ ~ ~ де Wк ,  cк і  к - результати вимірювань шляхової швидкості, кута зносу і кута курсу у момент t=tк відповідними датчиками. Передбачається, що справедливі співвідношення вигляду: ~ Wк  Wк 1   w    wк ; ~ cк  cк  c  cк (8) ; ~ к  к    к , де W - систематична помилка масштабного коефіцієнта допплерівського вимірника шляхової швидкості; Δс - систематична помилка вимірювання кута зносу; Δ - систематична помилка датчика курсу; ηWк, ημск, ηк - випадкові помилки типу дискретного «білого» шуму з нульовими середніми значеннями і відомими дисперсіями. Для побудови процедури курсо-допплерівського зчислення геоцентричних і географічних координат літального апарата використовують наступні формули [1]: 2 UA 70281 U W cos   c  d Rh 0 t ' t   '0   ; W sin   c  t    0   d R  hcos ' 0 t (9) , 5 10 15 20 25 30 35 де W(), с() - вимірювані допплерівською системою горизонтальна складова шляхової швидкості і кут зносу. Поточна географічна широта розраховується за формулою (5). Перевагами курсо-повітряної і курсо-допплерівської навігаційних систем є порівняна простота реалізації, автономність і безперервність отримання навігаційної інформації. До їх недоліків можна віднести необхідність задавання початкових значень координат і наявність ефекту нарощення помилок зчислення координат у часі (згідно із законом, близьким до лінійного). Для підвищення точності визначення навігаційних параметрів літальних апаратів до складу їх навігаційних комплексів, окрім курсо-швидкісних навігаційних систем, включають супутникову навігаційну систему, перевагою якої є висока точність вимірювання складових шляхової швидкості і координат місцеположення. До недоліків можна віднести можливість короткочасного зникнення сигналів від навігаційних супутників. З урахуванням формул курсо-повітряного і курсо-допплерівського зчислення частковоортодромічних координат (2), (7) і співвідношень (3), (8) неважко побудувати лінійні дискретні моделі еволюції у часі помилок курсо-повітряної і курсо-допплерівської навігаційних систем у визначенні координат (фіг 1). Завдяки лінійному характеру моделей еволюції помилок курсо-швидкісних навігаційних систем і введенню різницевих вимірювань (різниць поточних вихідних навігаційних параметрів курсо-швидкісних навігаційних систем і відповідних вихідних показань супутникової навігаційної системи, приведених до центра мас і перетворених у вибрану опорну систему координат), відомий спосіб комплексної обробки навігаційної інформації від курсо-швидкісної навігаційної системи і супутникової навігаційної системи зводиться до оцінювання помилок курсо-швидкісної навігаційної системи за допомогою оптимального лінійного дискретного фільтра і виправлення вихідних навігаційних параметрів курсо-швидкісної навігаційної системи з використанням оцінок її помилок, що одержуються на виході фільтра [3]. При цьому передбачається, що нормальна робота супутникової навігаційної системи (видача необхідної позиційно-швидкісної інформації) забезпечується при видимості не менше 4-х навігаційних супутників. Оскільки за наявності різницевих вимірювань за допомогою оптимального лінійного дискретного фільтра вдається одержати незміщені оцінки помилок курсо-швидкісної навігаційної системи, які практично не залежать від фактичних навігаційних параметрів (інваріантні до значень фактичних навігаційних параметрів), такий спосіб комплексної обробки навігаційної інформації називають інваріантним. Блок-схема розімкненої версії відомого інваріантного способу комплексної обробки навігаційної інформації представлена на фіг. 2, де використані наступні позначення: Z к - вектор-стовпець поточних вихідних параметрів курсо-швидкісної навігаційної системи  -го типу;  X к - вектор-стовпець помилок курсо-швидкісної навігаційної системи -  -го типу; ~ ~ снс ~ снс ~ снс T - вектор-стовпець різницевих вимірювань Yк  Xк  Хк , Zк  Zк , Wк  Wкснс , Wzк  Wzк для фільтра; Рк - коваріаційна матриця помилок оцінок фільтра; „-„ і „+„ - верхні індекси змінних до і після корекції у фільтрі; ~ ~ ~ ~  V , U ,  ,  Т , при   в ;  вк к вк к (10) Z к   ~ ~ ~ Т  Wк ,  с ,  к , при   д; к   40      Xк , Zк , U, в ,  Т , при   в ;  (11)  X к   Xк , Zк ,  W , в ,  Т , при   д.  снс Xк  Хк  хк ; (12) 3 UA 70281 U снс Zк  Zк  zк ; снс Wхк  Wxк  wхх ; снс Wzк  Wzк  wzк , 5 10 15 20 25 де: ηхк, ηzк, ηwхк, ηwzк - випадкові помилки супутникової навігаційної системи у вимірюванні частковоортодромічних координат і складових шляхової швидкості центра мас (типу дискретних «білих» шумів з нульовими середніми значеннями і відомими дисперсіями RC і wc відповідно); снс снс снс снс X к , Z к , Wхк , Wzк - показання супутникової навігаційної системи у момент t=tк, перетворені в частковоортодромічну систему координат і приведені до центра мас. До недоліків відомого інваріантного способу комплексної обробки навігаційної інформації від курсо-швидкісної навігаційної системи і супутникової навігаційної системи слід віднести низький рівень інтеграції (на рівні навігаційних систем), неурахування динамічних властивостей навігаційних параметрів і труднощі у використанні лінійної моделі еволюції помилок курсошвидкісної системи при тривалому часі безперервної роботи. Останній недолік може бути усунутий шляхом суттєвого ускладнення процедури обробки інформації при переході до замкненої версії інваріантного способу, що припускає періодичне введення зворотного зв'язку в курсо-швидкісну навігаційну систему за отриманими з виходу фільтра оцінками помилок курсошвидкісної системи [3]. Недоліків, властивих відомому інваріантному способу, позбавлений пропонований неінваріантний компенсаційний спосіб комплексної обробки навігаційної інформації від датчиків курсо-швидкісної навігаційної системи і супутникової навігаційної системи. Суть пропонованого способу зводиться до прямого оцінювання на кожному кроці обробки шуканих навігаційних параметрів літального апарата за допомогою нелінійного дискретного фільтра, в якому операцію оцінювання координат місцеположення центра мас літального апарата, поправок до показань датчиків і коваріаційної матриці помилок оцінок реалізують після одержання поточної позиційно-швидкісної інформації від супутникової навігаційної системи, а операцію екстраполяції оцінок координат на один крок виконують за допомогою відповідних формул курсо-швидкісного зчислення координат з використанням поточної інформації від датчиків з урахуванням оцінок поправок до показань цих датчиків. Блок-схема запропонованого способу представлена на фіг. 3, де позначено: X к - вектор оцінюваних параметрів для нелінійного дискретного фільтра; x к , zk , Uп , вп ,  п Т , при   в ;  (13) X к   х к , zk , w п ,  сп ,  п Т , при   д;  ∂Uп, ∂μп, ∂п, ∂wп, ∂μсп, ∂п - поправки до показань відповідних датчиків; 30 35   T снс снс снс Yк  xк , zк , wк , w снс - вектор спостережень для нелінійного дискретного фільтра; zк  =в - відповідає курсо-повітряній навігаційній системі;  =д - відповідає курсо-допплерівській навігаційній системі. Узагальнена дискретна модель еволюції вектора стану курсо-швидкісної навігаційної системи приймається у вигляді:   X к 1  f X к  Bк 1к  ;  =в, д. (14) Відповідно, узагальнене векторне рівняння спостережень має вигляд:    Yк  h X к  Dк 1к   G2  ,  =в, д. (15) к         У формулах (14) і (15): f X к і h X к - нелінійні вектор-функції відомого вигляду; B   , D  , G - матриці з відомими елементами: к 40 к   1к  ,  2к - вектори-стовпці випадкових дискретних «білих» шумів з нульовими середніми значеннями і одиничними дисперсіями. У використаному в запропонованому способі нелінійному дискретному фільтрі, який є нелінійною модифікацією заснованого на теоремі про нормальну кореляцію [6] узагальнюваного дискретного фільтра [5], операції корекції оцінок вектора стану X к і коваріаційної матриці 4 UA 70281 U помилок оцінок Рк виконуються після одержання позиційно-швидкісній інформації від супутникової навігаційної системи відповідно до наступних формул: ˆ ˆ ˆ   X   X   Р  Q Yк  h  X   ; (16)  к   к к       P    Р Q P T , (17) Pк к    5      D  D    GG  H P  H    ; T   T де P  Bк  Dк   Pк Hк  ; Q  Hк   10  T к  к   к  к  T  h X к ,  =в, д; Х к + - символ операції псевдообернення матриці: (-) і (+) - верхні індекси, відповідні значенням змінних до корекції і після корекції відповідно. Операція екстраполяції оцінок X к і Рк виконується на кожному кроці обробки згідно з формулами вигляду: ˆ ˆ Х к 1  f  Х к  ; (18)     Т Т Р  Ф Р Ф   В  В  , (19) к 1 к  де Фк   15  к T к   к к   к   ,  =в, д. f X к Х к Вирази вектор-функцій і матриць, що використовуються у формулах (14)-(19), мають наступний вигляд: а) для випадку  =в (курсо-повітряної навігаційної системи): ~  Vвк cos 1  3 cos  2   ~   Vвк sin 1  3 sin  2    ; (20) fв Xвк  Xвк  Т 0    0     0    Хк     Zк  hв Xвк   ~  (21)  Vвк cos 1  3 cos 2  ~   Vвк sin 1  3 sin 2  в  1к  і  2в  - вектори-стовпці дискретних «білих» шумів, що включають 7 і 4 компоненти к     20 відповідно:  Вкв  - матриця 5×7, у якій відмінні від нуля елементи: 25 b11=dcos1; b21=dsin1; b12=dcos2; b22=sin2; ~ b13=-d3sin2; b23=d3cos2; b14  dVвк sin 1 ; (22) ~ b 24  dVвк cos 1 ; b35=dξΔU; b46=dξμb; 1 b57=dξΔ; d  T 2 ; G - діагональна матриця 4×4, у якій відмінні від нуля елементи: g11=g22=RC; g33=g44=VС; (23)  Dкв  - матриця 4×7, у якій відмінні від нуля елементи: 30 d31=cos1; d41=sin1; d32=cos2; d42=sin2 ; ~ d33=-3sin2; d43=3cos2; b 34   Vвк sin 1 ; b 44   Vвк cos 1 ; (24) Ф в  - матриця 5×5, у якій відмінні від нуля елементи: к f11=f22=f33=f44=f55=1; f12=ΔTсоs2; f23=ΔTsin2; ~ ~ f14=-ΔT3sin2; f24=ΔT2cos2; f15   Vвк sin 1 ; f25  TVвк cos 1 ; (25) 5 UA 70281 U  Hкв  - матриця 4×5, у якій відмінні від нуля елементи: h11=h22=1; h33=cos2; h43=sin2; 34=-3sin2; ~ ~ h44=3cos2; h 35   Vвк sin 1 ; h 45  Vвк cos 1 ; (26) б) для випадку  =д (курсо-допплерівської навігаційної системи): 5   4 cos 5      4 sin 5   ; (27) f X к  X к  Т 0     0   0    Хк    Zк   (28) h X к    4 cos 5      sin   5   4   і    - вектори-стовпці дискретних «білих» шумів, що включають 6 і 4 компоненти Iк zк відповідно;  Вк  - матриця 5×6, у якій відмінні від нуля елементи:     10 15 b11=dcos5; b21=dsin5; b12=-d4sin5; b24=d4cos5; b13=-d4sin5; b23=d4cos5; b34=dξ∂w; b45=dξ∂μc; b56=dξΔ; 2 d=ΔT ; G - діагональна матриця вигляду (23);  Вк  - матриця 4×6, у якій відмінні від нуля елементи: d31=cos5; d41=sin5; d32=-4sin5; d42=-4cos5; d33=d32; d34=d42; (30)  Ф к  - матриця 5×5, у якій відмінні від нуля елементи: ~ ~ f11=f22=f33=f44=f55=1; f13  Tw к cos 5 ; f23  Tw к sin 5 ; 20 f14=-ΔT4sin5; f24=ΔT4cos5; (31) f15=f14; f25=f24;  Hк  - матриця 4×5, у якій відмінні від нуля елементи: ~ ~ h11=h22=1; h  w cos  ; h  w sin  ; 33 25 4 30 35 40 к 5 43 к 5 h34=-4sin5; h44=4cos5; h35=h34; h45=h44. (32) У формулах (20)-(32) використані такі позначення: ~ ~ 1   к   п   р ; 2=μвк+∂μвп-р; 3  Uк  Uп ; (33) ~ ~ ~   w 1  w  ;            , п 5 к п ск сп р ΔT - крок дискретності часу, співпадаючий з періодом оновлення інформації супутникової навігаційної системи. Пропонований неінваріантний компенсаційний спосіб комплексної обробки навігаційної інформації від датчиків курсо-швидкісної навігаційної системи (курсо-повітряного або курсодопплерівського типу) і від супутникової навігаційної системи забезпечує в порівнянні з відомим способом вищий рівень інтеграції (на рівні датчиків) та урахування динамічних властивостей шуканих навігаційних параметрів і, як наслідок, дає можливість підвищити точність навігації літальних апаратів. Крім того, пропонований спосіб відрізняється універсальністю по відношенню до типу курсо-швидкісної навігаційної системи і до вибору опорної навігаційної системи координат. Використані джерела: 1. Селезнев В.П. Навигационные устройства. - М.: Машиностроение, 1974. 2. Липчин Л.Ц. Проектирование сложных навигационных систем. - М.: Машиностроение, 1976. 3. Соловьев Ю.А. Спутниковая навигация и ее приложения. - М.: ЭКО-ТРЕНДЗ, 2003. 4. Бабич О.А. Обработка информации в навигационных комплексах. - М.: Машиностроение, 1991. 6 UA 70281 U 5. Захарин Ф.М. Методы и алгоритмы прикладного анализа. Выпуск 2. Статистическая фильтрация. - К.: КВВАИУ, 1978. 6. Липцер Р.Ш., Ширяев А.Н. Статистика случайных процессов. - М.: Наука,1974. 5 10 15 20 ФОРМУЛА КОРИСНОЇ МОДЕЛІ Спосіб комплексної обробки навігаційної інформації від датчиків курсо-швидкісної навігаційної системи і супутникової навігаційної системи літального апарата, що включає зчислення поточних координат місцеположення центру мас літального апарата у вибраній системі координат (частковоортодромічній, геоцентричній, географічній та ін.) за інформацією від датчиків курсо-швидкісної навігаційної системи, а також корекцію зчисленних координат за інформацією від супутникової навігаційної системи, який відрізняється тим, що оцінки поточних координат місцеположення центра мас літального апарата і поправок до показань датчиків курсо-швидкісної системи на кожному кроці обробки навігаційної інформації одержують за допомогою дискретного нелінійного фільтра, в якому операцію оцінювання координат місцеположення, поправок до показань датчиків і коваріаційної матриці помилок оцінок реалізують після одержання поточної позиційно-швидкісної інформації від супутникової навігаційної системи, а операцію екстраполяції оцінок координат місцеположення центра мас літального апарата виконують за допомогою формул курсо-швидкісного зчислення координат з використанням поточної інформації від датчиків з урахуванням оцінок поправок до показань цих датчиків. 7 UA 70281 U Комп’ютерна верстка А. Крулевський Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601 8