Спосіб частотної фільтрації та частотний фільтр для його здійснення

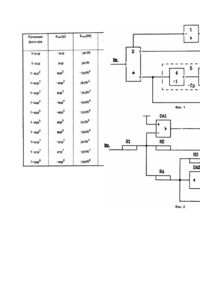
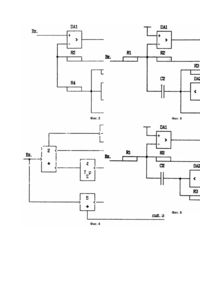
Изобретение относится к радиотехнике, связи и автоматическому регулированию, в частности, к частотной фильтрации сигналов. Известны аналоги способа, заключающиеся в том, что фильтр уемый сигнал умножат на функцию фильтрации с аппроксимирующим полиномом (многочленом) в знаменателе. В общем виде полином аппроксимации (апроксимирующий полином) представлен как где a, a2, ..., a n - постоянные положительные коэффициенты; n -натуральное число, определяющее порядок аппроксимации; p - оператор Лапласа. Первый аналог - способ заключается в том, что фильтруемый сигнал умножат на функцию с полиномом Бесселя, нормированные выражения которого приведены в табл.1 [1]. Способ фильтрации с использованием аппроксимации по Бесселю обеспечивает получение максимально линейной фазовочастотной характеристики (ФЧХ) и, соответственно, максимально равномерной характеристики группового времени задержки (ГВЗ). Для аппроксимации 2 - го порядка, независимо от вида аппроксимации, ФЧХ фильтра нижних частот (ФНЧ) равна при (p - угол "пи"), а характеристика ГВЗ которую можно записать в виде где W - частота; - постоянная составляющая времени задержки (Tзад(W) при W = 0); sTзад(W) - частотно-зависимое отклонение времени задержки от Tзад0. В полосе пропускания, в области нижних частот при Согласно (7), для аппроксимации по Бесселю, условием которой при n = 2 является a12/a2 = 3, Однако, обеспечивая максимально линейную ФЧХ и максимально равномерную характеристику ГВЗ (по сравнению со способами с другими видами аппроксимации), способ с аппроксимацией по Бесселю обеспечивает менее равномерную и с более пологим спадом, чем при рассматриваемом ниже способе с аппроксимацией по Баттерворту, амплитудно-частотную характеристику (АЧХ), что является недостатком способа. Кроме того, способ с аппроксимацией по Бесселю обладает недостатками, общими для всех видов аппроксимации. Это - наличие временной задержки Tзад0, которая будет больше при большем n, а также фазового сдвига, который, в общем случае, Второй аналог - способ заключается в том, что фильтруемый сигнал умножают на функцию с полиномом Баттерворта, нормированные выражения которого приведены в табл.2 ([1], с.190, табл.13.2). Способ обеспечивает получение максимально прямоугольной (среди други х известных способов) АЧХ которая в пределе, при n -> бск ("бск" бесконечность), представляет собой прямоугольную АЧХ идеального фильтра. Однако способ с аппроксимацией по Баттерворту приводит к нелинейной ФЧХ и, соответственно, к неравномерной характеристике ГВЗ. Характеристика ГВЗ, согласно (7), для аппроксимации по Баттерворту 2 - го порядка, для которой a12/a2 = 2, и, соответственно, согласно (5) и (6) и в отличие от (8), Нелинейность ФЧХ и, соответственно, неравномерность характеристики ГВЗ являются недостатком способа с аппроксимацией по Баттерворту. Кроме того, он обладает недостатками, общими для всех способов с известными аппроксимациями и рассмотренными выше (временная задержка и диапазон изменения фазы). Третий аналог - способ заключается в том, что фильтруемый сигнал умножают на функцию с полиномом, "переходным" между полиномами Бесселя и Баттерворта [2]. Однако при этом обеспечивается АЧХ, которая хуже, чем у способа с аппроксимацией по Баттерворту, и ФЧХ и характеристика ГВЗ, которые хуже, чем у способа с аппроксимацией по Бесселю. Кроме того, он также обладает общими недостатками, рассмотренными выше. Поставленная задача - устранить недостатки способов-аналогов и предложить способ, который обеспечил бы фильтрацию без временной задержки (во всей частотной области или в полосе пропускания) и без фазовых или с минимальными фазовыми (временными) искажениями, т.е. при При этом АЧХ должна быть максимально прямоугольной и, в пределе, при n ³ sск , прямоугольной АЧХ идеального фильтра. В равной мере сказанное должно относиться не только к фильтрации нижних частот, но и к фильтрации верхних часто т, полосовой (полоснопропускающей) и полосно-заграждающей фильтрации. Помимо сказанного, рассмотренные выше аналоги, а также способы с другими видами аппроксимации, не могут обеспечить частотное расщепление сигнала на две спектральные составляющие нижних и верхних частот с равномерными АЧХ, что обусловлено промежуточной спектральной группой полосовой фильтрации, определяемой для 2 - го порядка функцией которая в сумме с функциями фильтрации нижних и верхних частот на уровне 1/2; равна единице. Поэтому поставлена также задача, чтобы предлагаемый способ обеспечил расщепление сигнала на две спектральные группы с равномерными характеристиками нижних и верхних частот. При этом должна быть сохранена возможность полосовой фильтрации, а также полосно-заграждающей, которая для способованалогов характеризуется функцией В качестве прототипа выбран способ частотной фильтрации с аппроксимацией по Баттерворту. как наиболее близкий к заявляемому. Для осуществления поставленной задачи предлагается способ частотной фильтрации, при котором фильтруемый сигнал пропускают через цепь, характеризуемую аппроксимирующим полиномом в знаменателе передаточной функции. Согласно изобретению полином равен (бином), где an - коэффициент, определяющий частоту среза (в нормированном виде полином равен 1 ± pn при an = 1); n - натуральное число, определяющее порядок аппроксимации; p - оператор Лапласа. Предложенным способом могут быть осуществлены различные виды фильтрации, в том числе - нижних и вер хних частот, полосовой и полосно-заграждающей, а также других видов фильтрации. Передаточные функции фильтрации нижних частот и соответствующие АЧХ и ФЧХ, обусловленные полиномом (18) 1, ..., 8 - го порядков, приведены в табл.3. В соответствии с приведенными характеристиками свойства полинома (18) отличаются в зависимости от порядка, четного или нечетного. В общем виде, для полиномов нечетного порядка с частотой среза на уровне 1/21/2; (знаки в скобках соответствуют n = 3, 7, 11, ..., а без скобок - n = 1, 5, 9, ...), причем для n > 1 Из приведенных выражений следует: АЧХ (20) соответствует АЧХ (10) с аппроксимацией по Баттерворту; фаза, в отличие от (9) и независимо от n, - в пределах от 0 до ±p/2 (знак определяется знаком в (22)); характеристика ГВЗ равна нулю в начале диапазона частот. Для полиномов четного порядка где знак плюс - для четных значений n/2 и знак минус - для нечетных n/2, с частотой среза и, соответственно, Таким образом, предлагаемым способом частотной фильтрации обеспечивается выполнение поставленной задачи - фильтрация без задержки (Tзад = 0) и с минимальными фазовыми (временными) искажениями (sTзад(W) -> 0) для нечетных и вообще без искажений (sTзад(W) = 0) для четных значений n, АЧХ (20) и (25) максимально прямоугольны и в пределе, при n -> sск , - прямоугольные АЧХ идеального фильтра. Предлагается конкретизация способа, а именно: цепь, через которую пропускают фильтруемый сигнал, состоит из двух последовательно включенных цепей, одна из которых характеризуется аппроксимирующим полиномом другая - аппроксимирующем полиномом в знаменателях передаточных функций цепей, а коэффициенты обоих апроксимирующих полиномов равны коэффициентам полинома Баттерворта. В результате, аппроксимирующий полином цепи представляет собой произведение полиномов (29) и (30) и равен полиному (18). Для выполнения возможности расщепления сигнала на две спектральные составляющие, а также полосовой, полосно-заграждающей и других видов фильтрации - числитель передаточной функции равен При этом обеспечивается фильтрация верхних частот: - числитель передаточной функции равен При этом обеспечивается симметричная полосовая фильтрация; - числитель передаточной функции равен со знаком плюс при n/2 = 2, 6, ... и со знаком минус при n/2 = 4, 8, .... При этом обеспечивается симметричная полосно-заграждающая фильтрация; - числитель передаточной функции равен где s = 1, 2, ..., n - 1, кроме s = n/2. При этом обеспечивается асимметричная полосовая фильтрация. Особенность АЧХ при асимметричной фильтрации является то, что один из склонов АЧХ более крутой, а другой - более пологий; - числитель передаточной функции равен со знаком плюс при s = 2, 6, ... и со знаком минус, при s = 4, 8, .... При этом обеспечивается асимметричная полосно-заграждающая фильтрация. - числитель передаточной функции равен сумме сочетаний членов где 1 £ s £ n -1. При этом обеспечиваются различные виды комбинированной фильтрации. В частности, могут быть получены АЧХ для преобразования частотных изменений сигнала в амплитудные. Расщепление сигнала на две спектральные составляющие нижних и верхних частот обеспечивается согласно выражению (31), при котором функции фильтрации нижних и верхних частот в сумме равны единице (в отличие от аналогов, для 2 - го порядка которых равна единице сумма трех функций (14), (15) и (16), одна из которых является функцией полосовой фильтрации). Кроме того: - сигнал дополнительно пропускают через цепь с аппроксимирующим полиномом в знаменателе передаточной функции коэффициенты которого В частности, если сигнал пропускают через цепь с аппроксимирующим полиномом 1 -+ a1p (частный случай полинома (18)), дополнительное его пропускание через цепь, используемую при этом способе, обеспечит фильтрацию, характеризуемую полиномами согласно табл.3, а также полиномами более высоких порядков; - сигнал дополнительно пропускают через цепь с аппроксимирующим полиномом в знаменателе передаточной функции коэффициенты которого В частности, если сигнал пропускают через цепь с аппроксимирующим полиномом 1 - a2p2 (частный случай полинома (18)), дополнительное его пропускание через цепь, используемую при этом способе, обеспечит фильтрацию, характеризуемую полиномами (18) со значениями n, для которых n/2 нечетные. Указанные полиномы соответствуют полиномам, приведенным в табл.3, а также полиномам более высоких порядков. Рассмотрим аналоги фильтров. Первый аналог фильтра - это фильтр 1 - го порядка, содержащий трехполюсную (с одним общим выводом) цепь фильтрации (например, RC цепь), вход которой является входом, а общий вывод является общим выводом фильтра, и неинвертирующий усилитель, вход которого соединен с выходом цепи, а выход является выходом фильтра ([1], с.201, рис.13.10). Частотные свойства фильтра, определяются ограниченными свойствами пассивной цепи фильтрации. Второй аналог - это фильтр 2 - го порядка, содержащий цепь фильтрации с двумя общими выводами, вход которой является входом фильтра, а один общий вывод соединен с общим выводом фильтра, и неинвертирующий усилитель с коэффициентом усиления Kус = 1 (повторитель на операционном усилителе), вход которого соединен с выходом цепи, а выход - с другим общим выводом цепи и является выходом фильтра [3]. Второй аналог является эквивалентом LRC фильтра, для которого и, соответственно, для второго аналога где W0 - собственная частота фильтра; Q - добротность фильтра. Добротность LRC фильтра, как и второго аналога, а также рассматриваемых ниже других аналогов, положительна. Третий аналог - это фильтр 2 - го порядка, отличающийся от второго аналога тем, что Kус > 1 (определяется отрицательной обратной связью, обусловленной делителем из двух резисторов, вход которого соединен с выходом усилителя, а выход - с инвертирующим входом усилителя ([3], с.42, рис.4.2.6). Эквивалентом третьего аналога также является LRC фильтр. Четвертый аналог - это фильтр 2 - го порядка, содержащий цепь фильтрации с двумя общими выводами, вход которой является входом фильтра, а один общий вывод соединен с общим выводом фильтра, и инвертирующий усилитель с коэффициентом усиления Kус -> sск (операционный усилитель), вход которого соединен с выходом цепи, а выход - с другим общим выводом цепи и является выходом фильтра ([1], с.204, рис.13,15; с.214, рис.13.27; [3], с.40, рис.4.1.а). Четвертый аналог по своим свойствам соответствует второму аналогу. Рассмотренные аналоги фильтра с положительными постоянными времени и добротностями, тогда как для осуществления предложенных способов фильтрации необходимы отрицательные постоянные времени и добротности. Так, например, полином 1 - a1p реализуем при помощи цепи с постоянной времени T = -a1. Полином 1 - a2p2 реализуем при помощи цепи 2 - го порядка с T1 = a21/2 и T2 = -a21/2. Полином 1 - a1P + a2p2 реализуем при помощи цепи 2 - го порядка с Q = - a21/2/a1. Благодаря усиленной положительной обратной связи в третьем аналоге, можно было бы получить отрицательные постоянные времени и добротности, однако при этом фильтры возбуждаются, превращаясь в RC автогенераторы. В результате, для реализации предложенных способов фильтрации необходим новый "класс схем" фильтров. Ниже предложены соответствующие фильтры, у которых общим с аналогами является применение усилительного элемента (операционного усилителя). В этом смысле в качестве прототипа может быть принят, например, четвертый аналог фильтра. В соответствии со сказанным предлагается частотный фильтр, содержащий операционный усилитель, вы ход которого является выходом фильтра. Согласно изобретению, в него дополнительно введены цепь алгебраического суммирования с несколькими входами, один из входов которой является входом фильтра, другой соединен с выходом усилителя, цепь последовательно соединенных дифференциаторов с ±Tp, где T постоянные времени дифференциаторов, а p - оператор Лапласа, количество которых равно порядку фильтра, вход первого дифференциатора соединен с выходом усилителя, а вы ход последнего дифференциатора с третьим входом цепи суммирования и является вместе с выходами других ди фференциаторов другими выходами фильтра. Такой фильтр реализует способ 1 с полиномом 1 ±anpn и, соответственно, функции: а) на первом выходе фильтра (на выходе усилителя) - функцию фильтрации нижних частот где K1-2 - коэффициент усиления фильтра, определяемый отношением коэффициентов суммирования первого и второго входов цепи суммирования (например, K1-2 = 1); K3-2 - отношение коэффициентов суммирования третьего и второго входов цепи суммирования (например, K3-2 = 1); T1 ... Tn - произведение постоянных времени дифференциаторов; б) на выходе последнего, n го, дифференциатора - функция фильтрации верхних частот = R4 = 10кОм; C1 = 0,1мкФ; T = C1R 3 = 1мс; Fc p = 1/2ПТ = 1/2ПкГц - частота среза. Функции для схемы на фиг.2 соответствуют функциям, приведенным для схемы на фиг.1, умноженным на 1 (свойственно указанному виду обратной связи). 3. Фиг.3 - принципиальная схема фильтра с последовательной отрицательной обратной связью, соответствующая структурной схеме на фиг.1. Элементы схемы - те же, что и на схеме фиг.2, кроме отсутствующего R1 . Приведенные для схемы на фиг.1 функции умножаются на 2 (свойственно указанному виду обратной связи при R2 = R4). 4. Фиг.4 - структурная схема фильтра 2 - го порядка, характеризуемого полиномом и функциями в) на выходе s - го ди фференциатора (s =1, ..., n - 1) - функция симметричной и несимметричной полосовой фильтрации где Кроме того, в фильтре выход (1, ..., n - 1) - го дифференциатора соединен с четвертым входом цепи алгебраического суммирования. В равной мере это могут быть вы ходы всех или нескольких из числа указанных дифференциаторов. Дополнительно введена цепь алгебраического суммирования, выход которой соединен с входом s - го дифференциатора, один из входов - с вы ходом (s - 1) - го дифференциатора, а другой - с входом (1, ..., s - 1) - го дифференциатора. В равной мере цепь суммирования может иметь три и более входов, соединенных с входами други х (1, ..., s - 1) дифференциаторов. Кроме того, фильтр может содержать несколько цепей суммирования. Цепь суммирования может быть составной частью дифференциатора. Для получения функций комбинированной, в том числе полосно-заграждающей, фильтрации дополнительно введена цепь алгебраического суммирования, входы которой соединены один с входом, с другой с одним из выходов фильтра, а выход является дополнительным выходом фильтра. В равной мере дополнительных цепей суммирования может быть несколько - с разными функциями фильтрации. Изобретение поясняется следующими фигурами схем и характеристик: 1. Фиг.1 - структурная схема фильтра 1 - го порядка, характеризуемого полиномом и функциями (Вых. 1. Вых. 2), где: 1 - операционный усилитель ">" (входная цепь вынесена в цепь суммирования); 2 - цепь суммирования "+"; 3 - дифференциатор "Tp"; 4 - инвертор "-1"; 5 (3 и 4) - инвертирующий дифференциатор -Tp (с отрицательной постоянной времени). Фильтр на фиг.1 соответствует фильтру 1 (с одним дифференциатором). 2. Фиг.2 - принципиальная схема фильтра с параллельной отрицательной обратной связью, соответствующая структурной схеме на фиг.1, где DA1 и DA2 - операционные усилители; R1 = R2 = R3 (Вых. 1, Вых. 2, Вых. 3), где 1 - операционный усилитель ">" (входная цепь вынесена в цепь суммирования); 2 - цепь суммирования "+"; 3 инвертирующий дифференциатор "-T1p"; 4 неинвертирующий дифференциатор "T2p"; 5 дополнительная цепь суммирования "+". Фильтр на фиг.4 соответствует фильтру 4. 5. Фиг.5 - принципиальная схема фильтра 2 - го порядка с параллельной отрицательной обратной связью, соответствующая структурной схеме на фиг.4 (без цепи суммирования 5), и отличающаяся от схемы на фиг.2 наличием C2 (0,1мкФ) вместо R4. Конденсатор C2 выполняет функцию дифференциатора с T2p, где T 2 = C2R2. 6. Фиг.6 - принципиальная схема фильтра 2 - го порядка, отличающегося от фильтра на фиг.5 схемой включения DA2. Передаточная функция цепи, содержащей DA2, C1 и R3 , в результате полиномом чего фильтр характеризуется Включение DA2 (по схеме с последовательной отрицательной обратной связью) эквивалентно применению дифференциатора с передаточной функцией T1p и связи входа первого дифференциатора с входом второго - согласно фильтру 4, т.е. роль сумматора на входе 2 - го дифференциатора выполняет 1 й дифференциатор. Фильтр на фиг.6 соответствует фильтрам 1 и 4. 7. Фиг.7 - структурная схема фильтра 2 - го порядка, характеризуемого полиномом и функциями (Вых. 1, Вых. 2, Вых. 3), где 1 - операционный усилитель ">" (входная цепь вынесена в цепь суммирования); 2 - цепь суммирования "+"; 3 инвертирующий дифференциатор "-T1p"; 4 инвертирующий дифференциатор "-T2p". Фильтр на фиг.7 соответствует фильтру 2. 8. Фиг.8 - структурная схема фильтра 2 - го порядка, характеризуемого полиномом и функциями (Вых. 1, Вых. 2), где 1 - операционный усилитель ">" (входная цепь, вынесена в цепь суммирования); 2 цепь суммирования "+"; 3 - инвертирующий дифференциатор "-T1p"; 4 - инвертирующий дифференциатор "-T2p". Фильтр на фиг.8 соответствует фильтру 3 (дополнительная цепь суммирования на входе дифференциатора 4 совмещена с дифференциатором). 9. Фиг.9 - частотные характеристики ФНЧ и ФВЧ 4 - го порядка с передаточными функциями где V(2)/V(1) - АЧХ ФНЧ; V(3)/V(1) - АЧХ ФВЧ; VP(2) - ФЧХ ФНЧ; VP(3) - ФЧХ ФВЧ; VG(2) характеристика ГВЗ ФНЧ; VG(3) - характеристика ГВЗ ФВЧ; h - герц; Kh -килогерц: ud - микроградус; us - микросекунда (обозначения на фиг.9, а также на фиг.10, 11 и 12, обусловлены графикой ЭВМ), ФЧХ и характеристики ГВЗ равны нулю. 10. Фиг.10 - частотные характеристики полосового (ПП) и полосно-заграждающего (ПЗ) фильтров 4 - го порядка с передаточными функциями где V(2)/V(1) - АЧХ ПП; V(3)/V(1) - АЧХ ПЗ; VP(2) ФЧХ ПП; VP(3) - ФЧХ ПЗ; VG(2) - характеристика ГВЗ ПП; VG(3) - характеристика ГВЗ ПЗ, a h, Kh, ud и us - согласно обозначениям на фиг.9. ФЧХ и характеристики ГВЗ равны нулю. 11. Фиг.11 - частотные характеристики ФНЧ и ФВЧ 3 - го порядка с передаточными функциями где обозначения характеристик и величин согласно обозначениям на фиг.9, кроме: d - градус; ms - милисекунда. ФЧХ и характеристики ГВЗ равны нулю в полосе пропускания. 12. Фиг.12 - частотные характеристики амплитудно-частотного преобразователя 6 - го порядка с передаточной функцией где - передаточные функции асимметричной полосовой фильтрации; V(2)/V(1) - АЧХ преобразователя (построена со смещением на 0,5); VP(2) - ФЧХ преобразователя; VG(2) - характеристика ГВЗ преобразователя, а h, Kh; d и us - согласно обозначениям на фиг.9 и 10. ФЧХ и характеристики ГВЗ равны нулю. 13. Фиг.13 - структурная схема фильтра 1, где 1 операционный усилитель ">"; 2 -цепь алгебраического суммирования "+"; 3 - первый дифференциатор "±T1p"; 4 - n - й ди фференциатор "±Tnp"; "Bx." - вход фильтра; "Вых.1" - вы ход фильтра (выход усилителя); "Вых.2", ..., "Вых. (n - 1) -другие выходы фильтра (выходы 1, ..., n дифференциаторов). Предложенный способ (способы) фильтрации может быть осуществлен двумя путями - аппаратно и программно. Аппаратно способ осуществляется, в частности, предложенным фильтром (фильтрами). На фиг.1 - 8 и 13 приведены структурные и принципиальные схемы фильтров, а на фиг.9 - 12 частотные характеристики. Работа предложенных частотных фильтров определяется приведенными выше передаточными функциями фильтрации, соответствующими схемам. Полином функции фильтрации определяется передаточной функцией цепи обратной связи, а именно: - для фильтров на фиг.1, 4, 7 и 8 соответственно. Сигнал обратной связи, проходя через цепь с Kобр(p) и будучи умноженным на Kобр(p), сравнивается во входной цепи с входным сигналом фильтра. Вид фильтрации (нижних, верхних или други х частот) определяется тем, к какой части последовательной цепи дифференциаторов подключен выход фильтра: нижних частот - до дифференциаторов, что соответствует "н улевому" порядку члена в числителе функции фильтрации; верхних часто т - после последнего, n - го, дифференциатора, что соответствует n - му порядку члена в числителе; полосовой фильтрации - после s - го (s < n) дифференциатора, что соответствует s - му порядку члена в числителе функции фильтрации. Предложенный фильтр (фильтры) является устройством с отрицательной обратной связью, для которого важен вопрос обеспечения устойчивости. В общем случае в устройства х с отрицательной обратной связью возможны две причины неустойчивости. Во-первых, это частотнозависимая цепь, определяющая требуемую передаточную функцию устройства, и, во-вторых, паразитные фазосдвигающие цепи в операционных усилителях. Для определения того, устойчиво или неустойчиво устройство с обратной связью, пользуются петлевой передаточной функцией Kпет (p) и соответствующими частотными характеристиками Kпет (W) и F пет (W). В табл.4 приведены указанные функции и характеристики для фильтров с n = 1, ..., 8, а также показаны запасы по фазе в пределах "фазовой зоны" фильтров. Согласно табл.4, F пет (от W не зависит) для четных n - посередине "фазовой зоны", т.е. с запасом в пределах ±p/2, а для нечетных n - с запасом от 0 до p или от 0 до -p. Наличие запасов по фазе обеспечивает возможность осуществления устойчивости предложенных фильтров. Вопрос обеспечения устойчивости устройств с обратными связями и, в частности, на операционных усилителях известен и рассмотрен в литературе, например, в [1], с.82 ("7.4. Коррекция частотной характеристики"), с.145 ("11.5.2. Практическая реализация"), с.480 ("26. Электронные регуляторы"). Рассмотренные в [1] пути повышения устойчивости могут быть использованы в предложенном фильтре (фильтрах). В частности, это может быть введение корректирующи х цепей [1], с.82 и 480), применение "практической схемы" дифференциатора ([1], с.145). Кроме того, это может быть введение дополнительной связи с промежуточным отводом, подобно показанной на фиг.7. Возможность осуществления предложенного способа (способов) обусловлена приведенным анализом, а также предложенными фильтрами. Осуществление способа не исчерпывается предложенным фильтром (фильтрами). Способ может быть также осуществлен другими схемными решениями, в том числе цифровыми фильтрами, и, кроме того, он может быть осуществлен программно.