Спосіб визначення основних параметрів об’ємної структури металевих матеріалів
Номер патенту: 97453
Опубліковано: 10.02.2012
Автори: Даниленко Едуард Іванович, Даніленко Тетяна Петрівна
Формула / Реферат
1. Спосіб визначення основних параметрів об'ємної структури металевих матеріалів, який полягає в тому, що виготовляють шліф, отримують видиме зображення зеренної структури металу, вибирають на зображенні структури представницьку її область у сукупності не менш 3-х зерен, які межують одне з одним, наносять на цю область як групу паралельних рівновіддалених січних, так і перпендикулярну до неї другу ідентичну їй групу січних, вимірюють довжини хорд, що утворилися в результаті перерізу січних обох груп межами вибраної сукупності зерен, розподіляють заміряні довжини хорд у відносних частках ![]() по розмірних інтервалах у заданій розмірній шкалі і по отриманій сукупності вимірів хорд здійснюють реконструкцію розподілу
по розмірних інтервалах у заданій розмірній шкалі і по отриманій сукупності вимірів хорд здійснюють реконструкцію розподілу ![]() розмірів плоских перерізів зерен, а потім - реконструкцію розподілу
розмірів плоских перерізів зерен, а потім - реконструкцію розподілу ![]() розмірів тривимірних об'ємних зерен шляхом вирішення систем лінійних рівнянь і знаходять числові характеристики основних параметрів просторової структури в об'ємі, який відрізняється тим, що перед реконструкцією розподілу розмірів плоских перерізів зерен для урахування форми плоских перерізів визначають коефіцієнти їх форми
розмірів тривимірних об'ємних зерен шляхом вирішення систем лінійних рівнянь і знаходять числові характеристики основних параметрів просторової структури в об'ємі, який відрізняється тим, що перед реконструкцією розподілу розмірів плоских перерізів зерен для урахування форми плоских перерізів визначають коефіцієнти їх форми ![]() , для чого вибирають мінімальну статистично необхідну кількість типових за формою плоских перерізів, наносять на всю площину кожного з них під рівним кутом одна до другої не менше 8-ми груп паралельних рівновіддалених січних, вимірюють хорди, що утворилися в результаті перерізу січних межами цих типових плоских перерізів зерен, розподіляють заміряні хорди у відносних частках по розмірних інтервалах у заданій розмірній шкалі, знаходять для кожного розмірного інтервалу середні відносні частки хорд
, для чого вибирають мінімальну статистично необхідну кількість типових за формою плоских перерізів, наносять на всю площину кожного з них під рівним кутом одна до другої не менше 8-ми груп паралельних рівновіддалених січних, вимірюють хорди, що утворилися в результаті перерізу січних межами цих типових плоских перерізів зерен, розподіляють заміряні хорди у відносних частках по розмірних інтервалах у заданій розмірній шкалі, знаходять для кожного розмірного інтервалу середні відносні частки хорд ![]() від цих типових плоских перерізів зерен і визначають коефіцієнти форми
від цих типових плоских перерізів зерен і визначають коефіцієнти форми ![]() для кожного розмірного інтервалу шкали з відношення знайдених середніх відносних часток хорд від плоских перерізів зерен до відповідних розрахованих відносних часток хорд від кола; а реконструкцію розподілу розмірів плоских перерізів зерен здійснюють з урахуванням визначеної пропорційної залежності вірогідності потрапляння плоского перерізу зерна на січну лінію від його розміру шляхом вирішення системи лінійних рівнянь виду:
для кожного розмірного інтервалу шкали з відношення знайдених середніх відносних часток хорд від плоских перерізів зерен до відповідних розрахованих відносних часток хорд від кола; а реконструкцію розподілу розмірів плоских перерізів зерен здійснюють з урахуванням визначеної пропорційної залежності вірогідності потрапляння плоского перерізу зерна на січну лінію від його розміру шляхом вирішення системи лінійних рівнянь виду:
![]()
де:
![]() - кількість розмірних інтервалів у розмірній шкалі;
- кількість розмірних інтервалів у розмірній шкалі;
![]() - порядковий номер розмірного інтервалу від 1 до n;
- порядковий номер розмірного інтервалу від 1 до n;
![]() - довжини хорд k-го і (k-1)-го розмірних інтервалів; одиниці довжини;
- довжини хорд k-го і (k-1)-го розмірних інтервалів; одиниці довжини;
![]() - діаметри кругів, рівновеликих плоским перерізам зерен, відповідно, k-го, (k+1)-го,..., n-го розмірних інтервалів; одиниці довжини;
- діаметри кругів, рівновеликих плоским перерізам зерен, відповідно, k-го, (k+1)-го,..., n-го розмірних інтервалів; одиниці довжини;
![]() - відносна частка хорд k-го розмірного інтервалу;
- відносна частка хорд k-го розмірного інтервалу;
![]() - відносні частки плоских перерізів зерен, відповідно, k-го, (k+1)-го,..., n-го розмірних інтервалів;
- відносні частки плоских перерізів зерен, відповідно, k-го, (k+1)-го,..., n-го розмірних інтервалів;
![]() - коефіцієнти форми плоских перерізів зерен;
- коефіцієнти форми плоских перерізів зерен;
після чого отримують нормовані значення ![]() з відношення
з відношення ![]() потім перед реконструкцією розподілу розмірів тривимірних об'ємних зерен для урахування форми зерен визначають коефіцієнти форми
потім перед реконструкцією розподілу розмірів тривимірних об'ємних зерен для урахування форми зерен визначають коефіцієнти форми ![]() , для чого вибирають мінімальну статистично необхідну кількість типових за формою максимальних плоских перерізів зерен, присутніх на зображенні структури, наносять на всю площину кожного з них під рівним кутом одна до другої не менше 8-ми груп паралельних рівновіддалених січних, вимірюють хорди, що утворилися в результаті перерізу січних, межами цих типових максимальних плоских перерізів зерен, розподіляють заміряні хорди у частках по розмірних інтервалах у заданій розмірній шкалі, знаходять для кожного розмірного інтервалу середні відносні частки хорд
, для чого вибирають мінімальну статистично необхідну кількість типових за формою максимальних плоских перерізів зерен, присутніх на зображенні структури, наносять на всю площину кожного з них під рівним кутом одна до другої не менше 8-ми груп паралельних рівновіддалених січних, вимірюють хорди, що утворилися в результаті перерізу січних, межами цих типових максимальних плоских перерізів зерен, розподіляють заміряні хорди у частках по розмірних інтервалах у заданій розмірній шкалі, знаходять для кожного розмірного інтервалу середні відносні частки хорд ![]() від цих типових максимальних плоских перерізів зерен і визначають коефіцієнти форми
від цих типових максимальних плоских перерізів зерен і визначають коефіцієнти форми ![]() для кожного розмірного інтервалу шкали з відношення знайдених середніх відносних часток хорд до відповідних розрахованих відносних часток діаметрів плоских перерізів (кругів) від сфери; і далі, використовуючи як вихідну інформацію розраховані
для кожного розмірного інтервалу шкали з відношення знайдених середніх відносних часток хорд до відповідних розрахованих відносних часток діаметрів плоских перерізів (кругів) від сфери; і далі, використовуючи як вихідну інформацію розраховані ![]() або
або ![]() , знайдені безпосередніми вимірами діаметрів
, знайдені безпосередніми вимірами діаметрів ![]() на зеренній структурі і розподіленням їх у відносних частках по розмірних інтервалах, здійснюють реконструкцію розподілу розмірів тривимірних зерен з урахуванням пропорційної залежності вірогідності потрапляння тривимірного зерна на січну площину від його розміру, шляхом вирішення системи лінійних рівнянь виду:
на зеренній структурі і розподіленням їх у відносних частках по розмірних інтервалах, здійснюють реконструкцію розподілу розмірів тривимірних зерен з урахуванням пропорційної залежності вірогідності потрапляння тривимірного зерна на січну площину від його розміру, шляхом вирішення системи лінійних рівнянь виду:
![]()
де:
![]() - кількість розмірних інтервалів у розмірній шкалі;
- кількість розмірних інтервалів у розмірній шкалі;
![]() - порядковий номер розмірного інтервалу від 1 до n;
- порядковий номер розмірного інтервалу від 1 до n;
![]() - діаметри кругів, рівновеликих плоским перерізам зерен, відповідно, k-го, (k-1)-го розмірних інтервалів; одиниці довжини;
- діаметри кругів, рівновеликих плоским перерізам зерен, відповідно, k-го, (k-1)-го розмірних інтервалів; одиниці довжини;
![]() - діаметри сфер, рівновеликих тривимірним зернам, відповідно, k-го, (k+1)-го,..., n-го розмірних інтервалів; одиниці довжини;
- діаметри сфер, рівновеликих тривимірним зернам, відповідно, k-го, (k+1)-го,..., n-го розмірних інтервалів; одиниці довжини;
![]() - відносна частка плоских перерізів зерен k-го розмірного інтервалу;
- відносна частка плоских перерізів зерен k-го розмірного інтервалу;
![]() - відносні частки тривимірних зерен, відповідно, k-го, (k+1)-го,..., n-го розмірних інтервалів;
- відносні частки тривимірних зерен, відповідно, k-го, (k+1)-го,..., n-го розмірних інтервалів;
![]() – коефіцієнти форми тривимірних зерен,
– коефіцієнти форми тривимірних зерен,
після чого отримують нормовані значення ![]() з відношення
з відношення ![]() і знаходять числові характеристики основних параметрів просторової зеренної структури, а також сукупностей плоских і лінійних перерізів зерен.
і знаходять числові характеристики основних параметрів просторової зеренної структури, а також сукупностей плоских і лінійних перерізів зерен.
2. Спосіб за п. 1, який відрізняється тим, що для визначення коефіцієнтів форми плоских перерізів зерен ![]() для рівномірної розмірної шкали з будь-якою кількістю розмірних інтервалів спочатку знаходять розподіл довжин хорд
для рівномірної розмірної шкали з будь-якою кількістю розмірних інтервалів спочатку знаходять розподіл довжин хорд ![]() від статистично необхідної кількості типових за формою плоских перерізів зерен для рівномірної шкали з не менш як 7-ма розмірними інтервалами, шкала при цьому застосовується у відносному вигляді як:
від статистично необхідної кількості типових за формою плоских перерізів зерен для рівномірної шкали з не менш як 7-ма розмірними інтервалами, шкала при цьому застосовується у відносному вигляді як: ![]() представляють знайдений розподіл
представляють знайдений розподіл ![]() у графічному вигляді; в цих же осях координат будують відповідний графік розподілу відносних довжин хорд від кола
у графічному вигляді; в цих же осях координат будують відповідний графік розподілу відносних довжин хорд від кола ![]() , які розраховують за формулою
, які розраховують за формулою ![]() , і потім розраховують коефіцієнти форми
, і потім розраховують коефіцієнти форми ![]() для рівномірної шкали з необхідною кількістю розмірних інтервалів за формулою
для рівномірної шкали з необхідною кількістю розмірних інтервалів за формулою ![]() , знаходячи необхідні значення
, знаходячи необхідні значення ![]() і
і 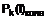 безпосередньо з побудованих графіків; далі аналогічним чином знаходять коефіцієнти форми тривимірних зерен
безпосередньо з побудованих графіків; далі аналогічним чином знаходять коефіцієнти форми тривимірних зерен ![]() для тієї ж розмірної шкали, для чого спочатку знаходять розподіл довжин хорд
для тієї ж розмірної шкали, для чого спочатку знаходять розподіл довжин хорд ![]() від статистично необхідної кількості типових за формою максимальних плоских перерізів зерен для рівномірної шкали з не менш як 7-ма розмірними інтервалами, шкала при цьому застосовується у відносному вигляді як:
від статистично необхідної кількості типових за формою максимальних плоских перерізів зерен для рівномірної шкали з не менш як 7-ма розмірними інтервалами, шкала при цьому застосовується у відносному вигляді як: ![]() представляють знайдений розподіл
представляють знайдений розподіл ![]() у графічному вигляді; в цих же осях координат будують відповідний графік розподілу відносних часток діаметрів кругів від сфери, які розраховують за формулою
у графічному вигляді; в цих же осях координат будують відповідний графік розподілу відносних часток діаметрів кругів від сфери, які розраховують за формулою ![]() , і потім розраховують коефіцієнти форми
, і потім розраховують коефіцієнти форми ![]() для рівномірної шкали з необхідною кількістю розмірних інтервалів за формулою
для рівномірної шкали з необхідною кількістю розмірних інтервалів за формулою ![]() , знаходячи необхідні значення
, знаходячи необхідні значення ![]() і
і ![]() безпосередньо з побудованих графіків.
безпосередньо з побудованих графіків.
3. Спосіб за п. 1, який відрізняється тим, що видимим зображенням зеренної структури може бути зображення плоских перерізів будь-яких елементів структури поліедричної, сферичної, еліпсоїдної та подібних їм форм, в тому числі неметалевих включень, графітної і цементитної фаз, вторинних фаз, інтерметалевих фаз та інших, для яких знаходять відповідні коефіцієнти форми їх плоских перерізів ![]() і коефіцієнти форми самих тривимірних елементів структури
і коефіцієнти форми самих тривимірних елементів структури ![]() .
.
Текст
1. Спосіб визначення основних параметрів об'ємної структури металевих матеріалів, який полягає в тому, що виготовляють шліф, отримують видиме зображення зеренної структури металу, вибирають на зображенні структури представницьку її область у сукупності не менш 3-х зерен, які межують одне з одним, наносять на цю область як групу паралельних рівновіддалених січних, так і перпендикулярну до неї другу ідентичну їй групу січних, вимірюють довжини хорд, що утворилися в результаті перерізу січних обох груп межами вибраної сукупності зерен, розподіляють заміряні довжини хорд у відносних частках Pk (l) по розмірних інтервалах у заданій розмірній шкалі і по отриманій сукупності вимірів хорд здійснюють реконструкцію розподілу Pk (d) розмірів плоских перерізів 2 3 97453 4 реконструкцією розподілу розмірів тривимірних об'ємних зерен для урахування форми зерен визначають коефіцієнти форми k , для чого вибирають мінімальну статистично необхідну кількість типових за формою максимальних плоских перерізів зерен, присутніх на зображенні структури, наносять на всю площину кожного з них під рівним кутом одна до другої не менше 8-ми груп паралельних рівновіддалених січних, вимірюють хорди, що утворилися в результаті перерізу січних, межами цих типових максимальних плоских перерізів зерен, розподіляють заміряні хорди у частках по розмірних інтервалах у заданій розмірній шкалі, знаходять для кожного розмірного інтервалу середні відносні частки хорд Pk (l)ср від цих типових числові характеристики основних параметрів просторової зеренної структури, а також сукупностей плоских і лінійних перерізів зерен. 2. Спосіб за п. 1, який відрізняється тим, що для визначення коефіцієнтів форми плоских перерізів зерен k для рівномірної розмірної шкали з будьякою кількістю розмірних інтервалів спочатку знаходять розподіл довжин хорд Pk (l)cр від статисти максимальних плоских перерізів зерен і визначають коефіцієнти форми k для кожного розмірного інтервалу шкали з відношення знайдених середніх відносних часток хорд до відповідних розрахованих відносних часток діаметрів плоских перерізів (кругів) від сфери; і далі, використовуючи як вихідну інформацію розраховані Pk (d) або гляді; в цих же осях координат будують відповідний графік розподілу відносних довжин хорд від кола Pk (l)кола , які розраховують за формулою Pk (d) , знайдені безпосередніми вимірами діаметрів dk на зеренній структурі і розподіленням їх у відносних частках по розмірних інтервалах, здійснюють реконструкцію розподілу розмірів тривимірних зерен з урахуванням пропорційної залежності вірогідності потрапляння тривимірного зерна на січну площину від його розміру, шляхом вирішення системи лінійних рівнянь виду: Pk (d) 1P(Dk ) 2 Dk 2 dk 1 2 2 2P(Dk 1 )( Dk 1 dk 1 2 2 2 2 Dk 1 dk ) ... n k 1P(Dn )( Dn dk 1 2 Dn 2 dk ), де: n - кількість розмірних інтервалів у розмірній шкалі; k - порядковий номер розмірного інтервалу від 1 до n; dk ; dk 1 - діаметри кругів, рівновеликих плоским перерізам зерен, відповідно, k-го, (k-1)-го розмірних інтервалів; одиниці довжини; Dk ;Dk 1;...;Dn - діаметри сфер, рівновеликих тривимірним зернам, відповідно, k-го, (k+1)-го,..., n-го розмірних інтервалів; одиниці довжини; Pk (d) - відносна частка плоских перерізів зерен kго розмірного інтервалу; P(Dk ); P(Dk 1);...;P(Dn ) - відносні частки тривимірних зерен, відповідно, k-го, (k+1)-го,..., n-го розмірних інтервалів; 1; 2 ;...;n k 1; – коефіцієнти форми тривимірних зерен, після чого отримують нормовані значення P(Dk ) з відношення n P(Dk ) P(Dk ) / P(Dk ) і знаходять k 1 чно необхідної кількості типових за формою плоских перерізів зерен для рівномірної шкали з не менш як 7-ма розмірними інтервалами, шкала при цьому застосовується у відносному вигляді як: l1 / lmax ;l2 / lmax ;...lk / lmax ;...lmax / lmax ; представляють знайдений розподіл Pk (l)cр у графічному ви 2 2 Pk (l)кола dk lk 1 , і потім розраховують коефі цієнти форми k для рівномірної шкали з необхідною кількістю розмірних інтервалів за формулою k Pk (l)cp / Pk (l)кола , знаходячи необхідні значення Pk (l)cр і Pk (l)кола безпосередньо з побудованих графіків; далі аналогічним чином знаходять коефіцієнти форми тривимірних зерен k для тієї ж розмірної шкали, для чого спочатку знаходять розподіл довжин хорд Pk (l)cр від статистично необхідної кількості типових за формою максимальних плоских перерізів зерен для рівномірної шкали з не менш як 7-ма розмірними інтервалами, шкала при цьому застосовується у відносному вигляді як: l1 / lmax ;l2 / lmax ;...lk / lmax ;...lmax / lmax ; представляють знайдений розподіл Pk (l)cр у графічному вигляді; в цих же осях координат будують відповідний графік розподілу відносних часток діаметрів кругів від сфери, які розраховують за формулою 2 2 Pk (d)сфери Dk dk 1 , і потім розраховують ко ефіцієнти форми k для рівномірної шкали з необхідною кількістю розмірних інтервалів за фор k Pk (l)cp / Pk (d)сфери , мулою знаходячи необхідні значення Pk (l)cр і Pk (d)сфери безпосередньо з побудованих графіків. 3. Спосіб за п. 1, який відрізняється тим, що видимим зображенням зеренної структури може бути зображення плоских перерізів будь-яких елементів структури поліедричної, сферичної, еліпсоїдної та подібних їм форм, в тому числі неметалевих включень, графітної і цементитної фаз, вторинних фаз, інтерметалевих фаз та інших, для яких знаходять відповідні коефіцієнти форми їх плоских перерізів k і коефіцієнти форми самих тривимірних елементів структури k . 5 Винахід належить до області металографічних досліджень і аналізу зеренної структури металевих матеріалів, способів визначення основних її параметрів. Формування регламентованої структури будьякого виробу забезпечується технологічним процесом його виготовлення, наприклад, зеренної структури - способами і параметрами пластичної деформації і термічної обробки, вибір яких здійснюють на підставі аналізу їх впливу на зернну структуру. Зазвичай металеві зеренні структури являють собою полідисперсні системи, тобто такі, що складаються з зерен різних розмірів. Найважливішою вихідною характеристикою таких полідисперсних систем є розподіл їх розмірів, який дозволяє розраховувати багато інших важливих кількісних параметрів структури: середній, максимальний, модальний розмір зерен, кількість зерен в одиниці 3 об'єму (наприклад, в 1 мм ), характеристики неоднорідності (розкиданості) розмірів - середньоквадратичне відхилення від середнього розміру, коефіцієнт варіації розподілу розмірів зерен та ін. Кількісні параметри зеренної структури впливають на властивості металів, тому регулюючи ці параметри можливо формувати необхідні властивості, а для цього необхідні способи якомога достовірнішого визначення параметрів. Через непрозорість металів для світла їх структуру найчастіше досліджують на металографічному шліфі, де зеренна структура представлена сукупністю багатокутників, якими є плоскі перерізи тривимірних (об'ємних) зерен, що мають форму різноманітних поліедрів (Салтыков С.А. Стереометрическая металлография. - М.: - 1970. - С. 276286). Але цей плоский переріз на шліфі є двовимірним зображенням реально існуючої тривимірної структури, саме яка і впливає на властивості. Тому задача формування певної структури, наприклад, з регламентованим середнім розміром зерен, є важливою і актуальною, і для її вирішення необхідно якомога достовірніше визначати параметри саме тривимірної об'ємної зеренної структури. Відомий спосіб визначення основних параметрів об'ємної структури (Салтыков С.А. Стереометрическая металлография. - М.: 1970. - С. 276-286), згідно з яким виготовляють шліф, отримують видиме зображення сферичних елементів структури на плоскому перерізі, встановлюють плоский переріз найбільшого діаметра, залежно від нього вибирають рівномірну розмірну шкалу з кількістю інтервалів не більше 15-ти; вимірюють діаметри плоских перерізів на всьому зображенні під мікроскопом з окуляр-мікрометром або на фотографії структури; розподіляють їх за розмірами в вибраній шкалі; визначають кількість елементів структури в кожній розмірній групі в частках, розраховують розподілення сферичних елементів структури за спеціальною формулою з використанням таблиці зі складовими формули. 97453 6 Недоліком даного способу є його обмежене застосування, оскільки він призначений до аналізу виключно елементів сферичної форми. Обмеженням є також використання розмірної шкали з кількістю інтервалів не більше 15-ти. Спосіб характеризується також низькою точністю через похибки складного процесу вимірювань діаметрів плоских перерізів. Відомий також спосіб визначення основних параметрів об'ємної структури матеріалів (Салтыков С.А. Стереометрическая металлография. - М.: 1970. - С. 286-291), який також призначений для аналізу структурних елементів виключно сферичної форми і який включає ту ж послідовність дій, що й за вище наведеним способом, але заміряні діаметри плоских перерізів сферичних частинок розподіляють в розмірній шкалі з 12-ма інтервалами, побудованій як геометричний ряд з множни-0,1 ком, що дорівнює 10 =0,79433, а розрахунок розподілу сферичних частинок за розмірами проводять за спеціальною формулою. Недоліком даного способу є його обмежене застосування, оскільки він призначений до аналізу виключно елементів сферичної форми. Обмеженням є також використання тільки однієї регламентованої нерівномірної розмірної шкали з 12-ма інтервалами. Спосіб характеризується також низькою точністю через похибки складного процесу вимірювань діаметрів плоских перерізів. Найбільш близьким за змістом є спосіб визначення основних параметрів структури металу (Патент України № 77135. - Опубл. 2006 - Бюл. №10), який полягає в тому, що виготовляють шліф, отримують видиме зображення зеренної структури металу, вибирають на зображенні представницьку область структури у сукупності не менше 3-х зерен, які межують одне з одним, наносять на неї як групу паралельних рівновіддалених січних, так і перпендикулярну до неї другу ідентичну групу січних, вимірюють довжини хорд, що утворилися в результаті перерізу січних обох груп межами вибраної сукупності зерен, розподіляють заміряні довжини хорд по розмірних інтервалах у заданій розмірній шкалі і проводять реконструкцію розподілу розмірів плоских перерізів зерен, а потім реконструкцію розподілу тривимірних зерен в об'ємі шляхом вирішення систем лінійних рівнянь; знаходять числові характеристики основних параметрів структури в об'ємі. Недоліком даного способу є обмежена його придатність тільки для структурних складових сферичної форми, про що свідчить вид його лінійних рівнянь для реконструкції розподілу зерен і їх плоских перерізів. При використанні даного способу для зеренних структур точність реконструкції розподілу розмірів зерен не є достовірною, оскільки: 1) форма зерен, згідно зі способом, приймається не поліедричною, якою вона є реально, а сферичною; 7 2) відсутнє рішення про врахування поліедричної форми металевих зерен; 3) не враховується існуюча пропорційна залежність вірогідності потрапляння плоских перерізів зерен на січну лінію і тривимірних зерен на січну площину від їх розмірів; 4) у формулі винаходу реконструкція розподілу розмірів плоских перерізів зерен некоректно названа «реконструкцією плоских перерізів», а реконструкція розподілу розмірів тривимірних зерен «реконструкцією об'ємної структури»; 5) не визначено, що є діаметром зерна на плоскому перерізі і що є діаметром зерна в об'ємі, адже об'ємне зерно є поліедром, а його плоский переріз на шліфі - багатокутником. Тому технологічні можливості застосування цього способу до визначення основних параметрів структури металевих матеріалів при встановленні впливу зеренної структури на властивості матеріалів, при розробці режимів їх термічної обробки, спрямованих на формування регламентованої структури, надто обмежені. В основу даного винаходу поставлена задача створення способу визначення основних параметрів об'ємної зеренної структури металевих матеріалів, який дозволяє врахувати реальну поліедричну форму металевих зерен і існуючу пропорційну залежність вірогідності потрапляння плоских перерізів зерен на січну лінію і тривимірних зерен на січну площину від їх розмірів шляхом зміни умов обробки видимого зображення структури на шліфі і прийомів по її реконструкції, що підвищує точність знайдених величин основних параметрів структури при одночасному забезпеченні розширення технологічних можливостей способу. Поставлена задача вирішується тим, що у способі визначення основних параметрів об'ємної структури металевих матеріалів, який полягає в тому, що виготовляють шліф, отримують видиме зображення зеренної структури металу, вибирають на зображенні структури представницьку її область у сукупності не менш 3-х зерен, які межують одне з одним, наносять на цю область як групу паралельних рівновіддалених січних, так і перпендикулярну до неї другу ідентичну їй групу січних, вимірюють довжини хорд, що утворилися в результаті перерізу січних обох груп межами вибраної сукупності зерен, розподіляють заміряні довжини хорд у відносних частках Рk(l) по розмірних інтервалах у заданій розмірній шкалі і по отриманій сукупності вимірів хорд здійснюють спочатку реконструкцію розподілу Pk(d) розмірів плоских перерізів зерен, а потім реконструкцію розподілу P(Dk) розмірів тривимірних об'ємних зерен шляхом вирішення систем лінійних рівнянь і знаходять числові характеристики основних параметрів просторової структури в об'ємі. При цьому, згідно з винаходом, перед реконструкцією розподілу розмірів плоских перерізів зерен для урахування форми плоских перерізів визначають коефіцієнти їх форми k , для чого вибирають мінімальну статистично необхідну кількість типових за формою плоских перерізів, наносять на всю площину кожного з них під рівним кутом одна до другої не менше 8-ми груп 97453 8 паралельних рівновіддалених січних, вимірюють хорди, що утворилися в результаті перерізу січних межами цих типових плоских перерізів зерен, розподіляють заміряні хорди у відносних частках по розмірних інтервалах у заданій розмірній шкалі, знаходять для кожного розмірного інтервалу середні відносні частки хорд Pk (l)cp від цих типових плоских перерізів зерен і визначають коефіцієнти форми k для кожного розмірного інтервалу шкали з відношення знайдених середніх відносних часток хорд від плоских перерізів зерен до відповідних розрахованих відносних часток хорд від кола; а реконструкцію розподілу розмірів плоских перерізів зерен здійснюють з урахуванням визначеної пропорційної залежності вірогідності потрапляння плоского перерізу зерна на січну лінію від його розміру шляхом вирішення системи лінійних рівнянь виду: 2 2 2 2 Pk (l) 1Pk (d) dk lk 1 2Pk 1(d)( dk 1 lk 1 2 2 2 2 2 _ dk 1 lk ) ... n k 1Pn (d)( dn lk 1 dn lk ), (1) де: n - кількість розмірних інтервалів у розмірній шкалі; k - порядковий номер розмірного інтервалу від 1 до n; lk ;lk 1 - довжини хорд k-го і (k-1)-го розмірних інтервалів; одиниці довжини; dk ; dk 1;...;dn - діаметри кругів, рівновеликих плоским перерізам зерен, відповідно, k-го, (k+1)го,..., n-го розмірних інтервалів; одиниці довжини; Pk (l) - відносна частка хорд k-го розмірного інтервалу; Pk (d); Pk 1(d);...;Pn (d) - відносні частки плоских перерізів зерен, відповідно, k-го, (k+1)-го,..., n-го розмірних інтервалів; 1; 2 ;...;n k 1; - коефіцієнти форми плоских перерізів зерен; після чого отримують нормовані значення Pk (d) з відношення Pk (d) Pk (d) / n Pk (d). k 1 Потім перед реконструкцією розподілу розмірів тривимірних об'ємних зерен для урахування форми зерен визначають коефіцієнти форми k , для чого вибирають мінімальну статистично необхідну кількість типових за формою максимальних плоских перерізів зерен, присутніх на зображенні структури, наносять на всю площину кожного з них під рівним кутом одна до другої не менше 8-ми груп паралельних рівновіддалених січних, вимірюють хорди, що утворилися в результаті перерізу січних межами цих типових максимальних плоских перерізів зерен, розподіляють заміряні хорди у частках по розмірних інтервалах у заданій розмірній шкалі, знаходять для кожного розмірного інтервалу середні відносні частки хорд Pk (l)cp від цих типових максимальних плоских перерізів зерен і визначають коефіцієнти форми k для кожного 9 97453 розмірного інтервалу шкали з відношення знайдених середніх відносних часток хорд до відповідних розрахованих відносних часток діаметрів плоских перерізів (кругів) від сфери. Далі, використовуючи як вихідну інформацію розраховані Pk (d) , або Pk (d) , знайдені безпосередніми вимірами діаметрів dk на зеренній структурі і розподіленням їх у відносних частках по розмірних інтервалах, здійснюють реконструкцію розподілу розмірів тривимірних зерен з урахуванням пропорційної залежності вірогідності потрапляння тривимірного зерна на січну площину від його розміру шляхом вирішення системи лінійних рівнянь виду: Pk (d) 1P(Dk ) 2 Dk 2 dk 1 2 2 2P(Dk 1 )( Dk 1 dk 1 Окрім того, в разі необхідності аналізу структури із застосуванням декількох шкал з різною кількістю розмірних інтервалів, для визначення коефіцієнтів форми плоских перерізів зерен k спочатку знаходять розподіл довжин хорд Pk (l)cp від статистично необхідної кількості типових за формою плоских перерізів зерен для рівномірної шкали з не менш як 7-ма розмірними інтервалами, шкала при цьому застосовується у відносному вигляді як: l1 / lmax ;l2 / lmax ;...lk / lmax ;...lmax / lmax ; представляють знайдений розділ Pk (l)cр у графічному вигляді; в цих же осях координат будують відповідний графік розподілу відносних довжин хорд від кола Pk (l)кола , які розраховують за формулою 2 2 P(l)кола dk lk 1 , і потім розраховують коефіці 2 2 2 2 Dk 1 dk ) ... n k 1P(Dn )( Dn dk 1 2 2 Dn dk ), (2) де: n - кількість розмірних інтервалів у розмірній шкалі; k - порядковий номер розмірного інтервалу від 1 до n; dk ; dk 1 - діаметри кругів, рівновеликих плоским перерізам зерен, відповідно, k-го, (k-1)-го розмірних інтервалів; одиниці довжини; Dk ;Dk 1;...;Dn - діаметри сфер, рівновеликих тривимірним зернам, відповідно, k-го, (k+1)-го,..., n-го розмірних інтервалів; одиниці довжини; Pk (d) - відносна частка плоских перерізів зерен k-го розмірного інтервалу; P(Dk ); P(Dk 1);...;P(Dn ) - відносні частки тривимірних зерен, відповідно, k-го (k+1)-го,..., n-го розмірних інтервалів; 1; 2 ;...;n k 1; – коефіцієнти форми тривимірних зерен, після чого отримують нормовані значення P(Dk ) з відношення P(Dk ) Pk (D) / 10 n P(Dk ) єнти форми k для рівномірної шкали з необхідною кількістю розмірних інтервалів за формулою k Pk (l)cp / Pk (l)кола , знаходячи необхідні значення Pk (l)cр і Pk (l)кола безпосередньо з побудованих графіків; далі аналогічним чином знаходять коефіцієнти форми тривимірних зерен k для тієї ж розмірної шкали, для чого спочатку знаходять розподіл довжин хорд Pk (l)cр від статистично необхідної кількості типових за формою максимальних плоских перерізів зерен для рівномірної шкали з не менш як 7-ма розмірними інтервалами, шкала при цьому застосовується у відносному вигляді як: l1 / lmax ;l2 / lmax ;...lk / lmax ;...lmax / lmax ; представляють знайдений розподіл Pk (l)cр у графічному вигляді; в цих же осях координат будують відповідний графік розподілу відносних часток діаметрів кругів від сфери, які розраховують за формулою 2 2 Pk (d)сфери Dk dk 1 , і потім розраховують ко ефіцієнти форми k для рівномірної шкали з необхідною кількістю розмірних інтервалів за формулою знаходячи k Pk (l)cp / Pk (d)сфери , і зна необхідні значення Pk (l)cр і Pk (d)сфери безпосе ходять числові характеристики основних параметрів просторової зеренної структури, а також сукупностей плоских і лінійних перерізів зерен. Числовими характеристиками основних параметрів структури можуть бути: розподіл розмірів тривимірних зерен P(Dk), їх плоских Pk(d) і лінійних Рk(l) перерізів (хорд); середній, максимальний, модальний розмір сукупності зерен, їх плоских і лінійних перерізів; кількість зерен в одиниці об'єму, їх плоских перерізів на одиниці площини, їх лінійних перерізів на одиниці довжини; середньоквадратичне відхилення від середнього розміру тривимірних зерен, їх плоских і лінійних перерізів; коефіцієнт варіації розподілу зерен, їх плоских і лінійних перерізів та ін. редньо з побудованих графіків. Пропонований спосіб може бути застосований і до визначення основних параметрів інших елементів структури поліедричної, сферичної, еліпсоїдної та подібних їм форм, в тому числі неметалевих включень, графітної і цементитної фаз, вторинних фаз, інтерметалевих фаз та ін., в цьому випадку видимим зображенням є зображення плоских перерізів цих елементів структури на шліфі. Для цих елементів структури теж визначають коефіцієнти форми k і k аналогічним пропонованому для зеренних структур способом. Технічним результатом пропонованого способу в порівнянні з найближчим з аналогів є підвищення точності знайдених величин основних параметрів структури при одночасному забезпеченні розширення технологічних можливостей способу. k 1 11 97453 Це обумовлено тим, що застосування коефіцієнтів форми k і k і спосіб їх знаходження, який заявляється, дозволяють реконструювати розподіл плоских перерізів зерен, а потім - розподіл тривимірних зерен саме поліедричної форми за формулами, які заявляються, що забезпечує широкі технологічні можливості способу, на відміну від прототипу, який хоча і запропонований для зеренеих структур, однак не враховує реальну поліедричну форму зерен, а розглядає її як сферичну, і тому дає помилкові результати. Спосіб визначення коефіцієнтів форми k і k , який заявляється, в якому використовуються графічні зображення розподілень, відповідно, довжин хорд від плоских перерізів зерен Pk (l)cр і від кола Рk(l)кола, і довжин хорд від максимальних плоских перерізів зерен Pk (l)cр і діаметрів кругів від сфери Pk(d)сфери, побудованих у спільних осях координат для рівномірної шкали з не менш як 7-ма розмірними інтервалами, спрощує у наступному процес знаходження коефіцієнтів форми для будьякої іншої рівномірної шкали з будь-якою кількістю розмірних інтервалів. Це значно розширює технологічні можливості способу. Вибір шкали з кількістю розмірних інтервалів не менше 7-ми обумовлений загально прийнятою металографічною 12 практикою (Салтыков С.А. Стереометрическая металлография. -М.: 1970. - С. 265). Пропонований спосіб враховує також визначену існуючу пропорційну залежність вірогідності потрапляння плоских перерізів зерен на січну лінію і тривимірних зерен на січну площину від їх розміру, в той час як у прототипі це для полідисперсних систем не враховується, оскільки склад формул обох реконструкцій за прототипом описує стан, коли всі зерна сферичної форми різного розміру мають однакову вірогідність потрапити на січну площину, а їх плоскі перерізи, кола, також мають однакову вірогідність потрапити на січну лінію, що не відповідає реальності. Для доказу останнього ствердження був проведений експеримент, згідно з яким, на сукупність кругів розмірами 50, 30 і 20 мм, взятих у рівній кількості і представлених на фігурі 1, нанесли рівновіддалені січні лінії згідно з пропонованим способом, і визначили кількість хорд, отриманих від кожної розмірної групи кругів. Результати експерименту наведені у таблиці 1 і вони свідчать про прямо пропорційну залежність потрапляння кругів на січну лінію від їх діаметра, тому кожен доданок формул переходу від розподілу розмірів хорд до розподілу розмірів плоских перерізів способупрототипу був помножений на відповідне dk, як міру цієї вірогідності, в результаті чого dk у чисельнику і знаменнику скоротилися і формули набули виду (7) пропонованого способу. Таблиця 1 Діаметр кругів dk, мм Відносна частка кругів P(dk) Співвідношення діаметрів кругів 50 30 20 0,3333 0,3333 0,3333 0,5 0,3 0,2 Доказ прямо пропорційної залежності потрапляння сфер на січну площину від їх діаметра був набутий в результаті експерименту, аналогічного попередньому. В цьому випадку круги на Фіг. 7 приймали за сукупності сфер, а січні лінії - за січні площини, перпендикулярні до площини з кругами. І відповідно до цієї залежності кожен доданок формул переходу від розподілу розмірів плоских перерізів зерен до розподілу розмірів тривимірних зерен способу-прототипу був помножений на відповідне Dk, як міру цієї вірогідності, в результаті чого Dk у чисельнику і знаменнику скоротилися і формули набули виду (2) пропонованого способу. Для зерен-поліедрів і їх плоских перерізівбагатокутників висновок про прямо пропорційну залежність їх потрапляння, відповідно, на січну площину і січну лінію від їх розмірів аналогічний наведеному вище, що ілюструє фігура 4, де видно, що чим більший розмір плоского перерізу зерна, тим більше хорд його перетинають. Окрім того у пропонованому способі надані чіткі визначення застосованих у формулах реконструкції складових, а саме, що d - це діаметри кругів, рівновеликих плоским перерізам елементів структури, a D - діаметри сфер, рівновеликих тривимір Кількість хорд, отриманих від кожної групи кругів, шт 924 555 368 Відносна частка хорд від кожної групи кругів 0,5 0,3 0,2 ним елементам структури, в той час як у способі прототипі роз'яснення цих понять відсутнє. Указане навело до двох систем лінійних рівнянь виду (7) і (2), які дозволяють реконструювати як розподіл розмірів плоских перерізів зерен, так і розподіл розмірів самих тривимірних зерен саме поліедричної форми, і на підставі вказаних розподілень - до визначення основних параметрів тривимірної структури і її плоских і лінійних перерізів, підвищивши тим самим точність способу і розширивши його технологічні можливості. На фігурі 7 представлена сукупність кругів розмірами 50, 30 і 20 мм, взятих у рівній кількості, зі схемою нанесення січних ліній. На фігурі 2 наведено приклад характерних форм плоских перерізів аустенітних зерен різного розміру (по центру кожного фото), на яких встановлювали коефіцієнти форми k . На фігурі 3 наведені напрямки (1-8) нанесення на плоский переріз аустенітного зерна 8-ми груп паралельних рівновіддалених січних і приклад нанесення січних напрямку 3 на зерно для визначення коефіцієнтів форми k . 13 На фігурі 4 зображено фото призначеної до аналізу представницької області зернистої структури однофазної сталі аустенітного класу з фрагментом нанесених січних ліній. На фігурі 5 наведено приклад характерних форм максимальних плоских перерізів зерен (по центру кожного фото), на яких встановлювали коефіцієнти форми k . На фігурі 6 представлено встановлений вихідний розподіл довжин хорд Рk(l) (△− −△) і реконструйовані за пропонованим способом розподіли діаметрів плоских перерізів зерен Pk (d) (○− −○) і діаметрів тривимірних зерен P'(Dk) ( ) для структури, зображеної на фігурі 4. На фігурі 7 представлено графіки експериментально встановленого для шкали з 10-ма інтервалами розподілу середніх відносних часток хорд Pk (l)cр від 20-ти типових за формою плоских перерізів зерен аустеніту ( ) (їх приклади наведені на Фіг. 2) і розрахованого розподілу відносних часток хорд від кола Рk(l)кола (○− −○), використовуючи які слід знаходити коефіцієнти форми k для розмірної шкали з будь-якою кількістю розмірних інтервалів. Пропонований спосіб здійснюють таким чином. Зразки шліфують, полірують і піддають травленню для виявлення зеренної структури, а саме, плоских перерізів тривимірних зерен. Видиме зображення плоских перерізів зерен на шліфі фотографують або досліджують за допомогою мікроскопа або аналізаторів структури. Обробку отриманого видимого зображення плоских перерізів зерен і реконструкцію структури здійснюють, наприклад, за допомогою комп'ютера, на екран дисплея якого виводять зображення зеренної структури, і спочатку для урахування форми плоских перерізів зерен визначають коефіцієнти їх форми k , для чого вибирають мінімальну статистично необхідну кількість типових за формою плоских перерізів, наносять на всю площину кожного з них під рівним кутом одна до другої не менше 8-ми груп паралельних рівновіддалених січних, вимірюють довжини хорд l, що утворилися в результаті перерізу січних межами цих типових плоских перерізів зерен, розподіляють заміряні хорди у відносних частках Рk(l) по розмірних інтервалах у заданій розмірній шкалі, знаходять для кожного розмірного інтервалу середні відносні частки хорд Рk(l)ср від цих типових плоских перерізів зерен і визначають коефіцієнти форми k для кожного розмірного інтервалу шкали з відношення знайдених середніх відносних часток хорд плоских перерізів зерен до відповідних розрахованих відносних часток хорд від кола; тобто 2 2 k Pk (l)cp / Pk (l)кола , де P(l)кола dk lk 1 . Далі вибирають на зображенні структури представницьку її область у сукупності не менш 3х зерен, які межують одне з одним, наносять на цю область як групу паралельних рівновіддалених січних, так і перпендикулярну до неї другу ідентичну їй групу січних, вимірюють довжини хорд, що 97453 14 утворилися в результаті перерізу січних обох груп межами вибраної сукупності зерен, розподіляють заміряні довжини хорд у відносних частках Рk(l) по розмірних інтервалах у заданій розмірній шкалі і потім по отриманій сукупності вимірів хорд здійснюють реконструкцію розподілу Pk(d) розмірів плоских перерізів зерен з урахуванням визначеної пропорційної залежності вірогідності потрапляння плоского перерізу зерна на січну лінію від його розміру шляхом вирішення систем лінійних рівнянь виду: 2 2 Pk (l) 1Pk (d) dk lk 1 2 2 2Pk 1(d)( dk 1 lk 1 2 2 2 2 2 dk 1 lk ) ... n k 1Pn (d)( dn lk 1 dn lk ), де: n - кількість розмірних інтервалів у розмірній шкалі; k - порядковий номер розмірного інтервалу від 1 до n; lk ;lk 1 - довжини хорд k-го і (k-1)-го розмірних інтервалів; одиниці довжини; dk ; dk 1;...;dn - діаметри кругів, рівновеликих плоским перерізам зерен, відповідно, k-го, (k+1)го,..., n-го розмірних інтервалів; одиниці довжини; Pk (l) - відносна частка хорд k-го розмірного інтервалу; Pk (d); Pk 1(d);...;Pn (d) - відносні частки плоских перерізів зерен, відповідно, k-го, (k+1)-го,..., n-го розмірних інтервалів; 1; 2 ;...;n k 1; - коефіцієнти форми плоских перерізів зерен; після чого отримують нормовані значення Pk (d) з відношення Pk (d) Pk (d) / n Pk (d). k 1 Далі для урахування форми тривимірних зерен визначають коефіцієнти їх форми k , для чого вибирають мінімальну статистично необхідну кількість типових за формою максимальних плоских перерізів зерен, присутніх на зображенні структури, наносять на всю площину кожного з них під рівним кутом одна до другої не менше 8-ми груп паралельних рівновіддалених січних, вимірюють довжини хорд l, що утворилися в результаті перерізу січних межами цих типових максимальних плоских перерізів зерен, розподіляють заміряні хорди у відносних частках Рk(l) по розмірних інтервалах у заданій розмірній шкалі, знаходять для кожного розмірного інтервалу середні відносні частки хорд Pk (l)ср від цих максимальних типових плоских перерізів зерен і визначають коефіцієнти форми k для кожного розмірного інтервалу шкали з відношення знайдених середніх відносних часток хорд від цих максимальних плоских перерізів зерен до відповідних розрахованих відносних часток діаметрів плоских перерізів від сфери, тоб 15 то 97453 k Pk (l)cp / Pk (d)сфери , де 2 2 Pk (d)сфери Dk dk 1 . Потім, використовуючи знайдені Pk (d) як вихідну інформацію, здійснюють реконструкцію розподілу розмірів тривимірних зерен з урахуванням пропорційної залежності вірогідності потрапляння тривимірного зерна на січну площину від його розміру шляхом вирішення системи лінійних рівнянь виду: 2 2 Pk (d) 1P(Dk ) Dk dk 1 2 2 2P(Dk 1 )( Dk 1 dk 1 2 2 2 2 Dk 1 dk ) ... n k 1P(Dn )( Dn dk 1 2 2 Dn dk ), де: n - кількість розмірних інтервалів у розмірній шкалі; k - порядковий номер розмірного інтервалу від 1 до n; dk ; dk 1 - діаметри кругів, рівновеликих плоским перерізам зерен, відповідно, k-го, (k-1)-го розмірних інтервалів; одиниці довжини; Dk ;Dk 1;...;Dn - діаметри сфер, рівновеликих тривимірним зернам, відповідно, k-го, (k+1)-го,..., n-го розмірних інтервалів; одиниці довжини; Pk (d) - відносна частка плоских перерізів зерен k-го розмірного інтервалу; P(Dk ); P(Dk 1);...;P(Dn ) - відносні частки тривимірних зерен, відповідно, k-го (k+1)-го,..., n-го розмірних інтервалів; 1; 2 ;...;n k 1; – коефіцієнти форми тривимірних зерен, після чого отримують нормовані значення P(Dk ) з відношення P(Dk ) Pk (D) / n P(Dk ) і зна k 1 ходять числові характеристики основних параметрів просторової зеренної структури, а також сукупностей плоских і лінійних перерізів зерен. Як вихідну інформацію для реконструкції розподілення P(Dk) може застосовуватися також розподілення Pk(d), встановлене безпосередніми вимірами діаметрів dk на структурі і розподіленням їх у відносних частках по розмірних інтервалах. В разі необхідності аналізу структури із застосуванням декількох шкал з різною кількістю розмірних інтервалів, для визначення коефіцієнтів форми плоских перерізів зерен k спочатку знаходять розподіл довжин хорд Рk(l)ср від статистично необхідної кількості типових за формою плоских перерізів зерен для рівномірної шкали з не менш як 7ма розмірними інтервалами і представляють цей розподіл у графічному вигляді, шкала при цьому застосовується у відносному вигляді як: l1 / lmax ;l2 / lmax ;...lk / lmax ;...lmax / lmax ; в цих же осях координат будують відповідний графік розподілу відносних довжин хорд від кола рk(l)кола, які розра 16 2 2 ховують за формулою P(l)кола dk lk 1 , і потім розраховують коефіцієнти форми плоских перерізів зерен k для рівномірної шкали з необхідною кількістю розмірних інтервалів за формулою k Pk (l)cp / Pk (l)кола , знаходячи необхідні значен ня Pk (l)cр і Pk (l)кола безпосередньо з побудованих графіків. Далі аналогічним чином знаходять коефіцієнти форми тривимірних зерен k, для чого розподіл довжин хорд Pk (l)cр , отриманих від статистично необхідної кількості типових за формою максимальних плоских перерізів зерен для рівномірної шкали з 7-ма розмірними інтервалами, представляють у графічному вигляді, шкала при цьому застосовується у відносному вигляді як: l1 / lmax ;l2 / lmax ;...lk / lmax ;...lmax / lmax ; в цих же осях координат будують відповідний графік розподілу відносних часток діаметрів кругів від сфери, які розраховують за формулою 2 2 Pk (d)сфери Dk dk 1 , і потім розраховують ко ефіцієнти форми k для рівномірної шкали з необхідною кількістю розмірних інтервалів за формулою k Pk (l)cp / Pk (d)сфери , знаходячи необхідні значення Pk (l)cр і Pk (d)сфери безпосередньо з побудованих графіків. Пропонований спосіб може бути застосований і до визначення основних параметрів інших елементів структури поліедричної, сферичної, еліпсоїдної та подібних їм форм, в тому числі неметалевих включень, графітної і цементитної фаз, вторинних фаз, інтерметалевих фаз та ін., в цьому випадку видимим зображенням є зображення плоских перерізів цих елементів структури на шліфі. Для цих елементів структури теж визначають коефіцієнти форми k і k пропонованим для зеренних структур способом. Як приклад пропонований спосіб був застосований до аналізу зеренної структури наступним чином. Для аналізу зеренної структури за пропонованим способом з труби розмірами 6,9x0,4 мм (сталь 026X16Н15МЗБ) виготовили металографічний шліф, який для виявлення зеренної мікроструктури протруїли в азотній кислоті і за допомогою металографічного мікроскопа МІМ-7 отримали зображення плоского перерізу зеренної структури (плоских перерізів зерен). Потім для визначення коефіцієнтів форми k візуально проаналізували під мікроскопом форму плоских перерізів зерен, вибрали мінімальну статистично необхідну кількість типових форм різного розміру у 20 шт., сфотографували їх (Фіг. 2) і на кожне зображення нанесли під кутом 22,5° одна до другої 8 груп паралельних січних (Фіг. 3), заміряли довжини отриманих хорд; для кожного плоского зерна встановили максимальну хорду Іmах і розміри усіх хорд від цього плоского зерна представили у відносному вигляді l/lmax, а потім розподілили їх у частках в рівномірній розмірній шкалі з 10-ма інтервалами; далі знайшли середні частки хорд 17 97453 Pk (l)cр по кожному розмірному інтервалу для 20 ти типових форм плоских зерен і визначили коефіцієнти форми плоских перерізів зерен k для кожного розмірного інтервалу з відношення знайдених Pk (l)cр до відповідних розрахованих відносних 18 часток хорд від кола: k Pk (l)cp / Pk (l)кола , де 2 2 P(l)кола dk lk 1 . Коефіцієнти форми k наве дені у таблиці 2. Таблиця 2 1 0,188 2 1,063 3 1,669 4 1,904 5 1,664 Потім, вибравши представницьку область зеренної структури (Фіг. 4), ввели це зображення в комп'ютер, нанесли на зображення дві групи паралельних рівновіддалених один від одного січних у двох взаємно перпендикулярних напрямках, заміряли довжини всіх отриманих хорд і 6 1,607 7 1,710 8 2,036 9 3,259 10 6,563 розрахували розподіл їх по розмірних групах у рівномірній шкалі з 10-ма розмірними інтервалами з кроком 15,6 мкм, виходячи з того, що максимальна хорда становила 156 мкм. Результати отриманих вимірів наведені в таблиці 3. Таблиця 3 №№ інтервалів k Межі інтервалів Іmin – Іmax, МКМ 1 2 3 4 5 6 7 8 9 0 0-15,6 15,6-31,2 31,2-46,8 46,8 - 62,4 62,4 - 78,0 78,0-93,6 93,6-109,2 109,2-124,8 124,8-140,4 140,4-156,0 Кількість хорд по інтер- Відносні частки хорд, P (l) k валах, шт. 656 0,1128117 1444 0,2483233 1494 0,2569218 1084 0,1864145 616 0,1059329 300 0,0515907 136 0,0233878 60 0,0103181 21 0,0036113 4 0,0006879 Для знаходження розподілу діаметрів плоских перерізів зерен Pk(d) склали наступну систему рівнянь виду (7): 0,0006879 = 0,188P10(d) 1562 140,4 2 ; 0,0036113 = 0,188P9(d) 140,4 2 124,8 2 + 1,063P10(d) ( 1562 124,8 2 - 1562 140,4 2 ); 0,0103181=0,188P8(d) 124,8 2 109,2 2 +1,063P9(d)( 140,4 2 109,2 2 140,4 2 124,8 2 )+1,669P10(d) 1562 109,2 2 - 1562 124,8 2 ); 0,0233878=0,188P7(d) 109,2 2 93,6 2 +1,063Р8(d)( 124,8 2 93,6 2 - 124,8 2 109,2 2 )+1,669 P9(d)( 140,4 2 93,6 2 140,4 2 109,2 2 )+1,904P10(d)( 1562 93,6 2 - 1562 109,2 2 ); 0,0515907=0,188P6(d) 93,6 2 782 +1,063Р7(d)( 109,2 2 78 2 109,2 2 93,6 2 )+…+1,664P10(d)( 1562 782 1562 93,6 2 ); 0,1059329=0,188P5(d) 782 62,4 2 +1,063P6(d)( 93,6 2 62,4 2 93,6 2 782 )+…+1,607P10(d)( 1562 62,4 2 0,1864145 = 1562 782 ); 0,188Р4(d) 62,4 2 46,8 2 +1,063P5(d)( 782 46,8 2 - 782 62,4 2 )+...+1,710P10(d) ( 1562 46,8 2 - 1562 62,4 2 ); , , 0,2569218=0,188P3(d) 46,8 2 312 2 +1,063P4(d)( 62,4 2 312 2 62,4 2 46,8 2 +…+2,036P10(d)( 1562 312 2 , 1562 46,8 2 ); 19 97453 20 , 0,2483233=0,188P2(d) 312 2 15,6 2 +1,063P3(d)( 46,8 2 15,5 2 46,8 2 312 2 +…+3,259P10(d)( 1562 15,6 2 , 1562 312 2 ); , , , 0,1128117=0,188P1(d) 15,6 2 0 +1,063P2(d)( 31 2 2 0 - 312 2 15,6 2 )+…+6,563P10(d)( 1562 0 1562 15,6 2 ). Вирішили наведену систему рівнянь, наприклад, за допомогою комп'ютера, в результаті чого знайшли всі значення Pk(d), після чого отримали нормовані значення P'k(d) із співвідношення P(dk ) Pk (d) / n Pk (d) , які у сукупності являють собою розподіл діаметрів плоских перерізів зерен і який є вихідним для наступної реконструкції розподілу діаметрів зерен в об'ємі. Отримані результати реконструкції наведені в таблиці 4. k 1 Таблиця 4 №№ інтервалів k Межі інтервалів lmin – lmax, мкм 1 0-15,6 2 15,6-31,2 3 31,2-46,8 4 46,8 - 62,4 5 62,4-78,0 6 78,0-93,6 7 93,6-109,2 8 109,2-124,8 9 124,8-140,4 10 140,4-156,0 Розраховані відносні частки Рk(d) 0,0015308 0,0058669 0,0082069 0,0071468 0,0042715 0,0020821 0,0007992 0,0003700 0,0001776 0,0000538 Потім визначили коефіцієнти форми k для реконструкції розподілу діаметрів тривимірних зерен. Для цього візуально проаналізували під мікроскопом форму максимальних плоских перерізів зерен, вибрали мінімальну статистично необхідну кількість типових форм у 20 шт, сфотографували їх і на кожне зображення нанесли під кутом 22,5 одна до другої 8 груп паралельних січних, заміряли довжини отриманих хорд; для кожного плоского зерна встановили максимальну хорду Іmах і розміри усіх хорд від цього плоского зерна представили у відносному вигляді l/l mах, потім розподілили їх у відносних частках в рівномірній розмірній шкалі з 10-ма інтервалами. Знайдені частки хорд Рк(і), згідно з винаходом (А.с. СССР № 1397832. - Опубл. 1988 - Бюл. № Розподіл діаметрів плоских перерізів зерен (нормовані відносні частки) P'k(d) 0,0501813 0,1923221 0,2690290 0,2342776 0,1400243 0,0682534 0,0261979 0,0121302 0,0058203 0,0017639 19), приймали за відносні частки розмірів плоских перерізів Pk(d) від тих тривимірних зерен, на максимальні плоскі перерізи яких були нанесені січні лінії. Після цього знайшли середні частки Pk(d)cp по кожному розмірному інтервалу для 20-ти проаналізованих типових форм плоских зерен і визначили коефіцієнти форми k для кожного розмірного інтервалу з відношення знайдених Pk(d)cp до відповідних розрахованих відносних часток діаметрів кругів від сфери: де k Pk (l)cp / Pk (d)сфери , 2 2 Pk (d)сфери Dk dk 1 . Коефіцієнти форми k наведені у таблиці 5. Таблиця 5 1 0,218 2 1,186 3 1,657 4 1,807 5 1,595 Знайдений розподіл діаметрів плоских перерізів зерен (нормовані відносні частки P'k(d)) застосували як вихідну інформацію до реконструкції розподілу діаметрів тривимірних зерен в об'ємі, а 6 1,478 7 1,520 8 1,773 9 3,277 10 6,749 саме для знаходження відносних часток P(Dk). Для цієї реконструкції склали наступну систему рівнянь виду (2): 0,0017639=0,218P(D10) 1562 140,4 2 ; 0,0058203=0,218P(D9) 140,4 2 124,8 2 + 1,186P(D10)( 1562 124,8 2 - 1562 140,4 2 ); 21 97453 22 0,0121302=0,218P(D8d) 124,8 2 109,2 2 +1,186P(D9)( 140,4 2 109,2 2 140,4 2 124,8 2 )+1,657P(D10) 1562 109,2 2 - 1562 124,8 2 ); 0,0261979=0,218P(D7) 109,2 2 93,6 2 +1,186Р(D8)( 124,8 2 93,6 2 124,8 2 109,2 2 )+1,657P(D9)( 140,4 2 93,6 2 140,4 2 109,2 2 )+1,807P(D10)( 1562 93,6 2 1562 109,2 2 ); 0,0682534=0,218P(D6) 93,6 2 782 +1,186Р(D7)( 109,2 2 78 2 109,2 2 93,6 2 )+…+1,595P(D10)( 1562 782 1562 93,6 2 ); 0,1400243=0,218P(D5) 782 62,4 2 +1,186P(D6)( 93,6 2 62,4 2 93,6 2 782 )+…+1,478P(D10)( 1562 62,4 2 1562 782 ); 0,2342776=0,218Р(D4) 62,4 2 46,8 2 +1,186P(D5)( 782 46,8 2 782 62,4 2 )+...+1,520P(D10)( 1562 46,8 2 - 1562 62,4 2 ); , , 0,2690290=0,218P(D3) 46,8 2 312 2 +1,186P(D4)( 62,4 2 312 2 62,4 2 46,8 2 +…+1,773P(D10)( 1562 312 2 , 1562 46,8 2 ); , 0,1923221=0,218P(D2) 312 2 15,6 2 +1,186P(D3)( 46,8 2 15,5 2 46,8 2 312 2 +…+3,277P(D10)( 1562 15,6 2 , 1562 312 2 ); , , , 0,0501813=0,218P(D1) 15,6 2 0 +1,186P(D2)( 31 2 2 0 - 312 2 15,6 2 )+…+6,749P(D10)( 1562 0 1562 15,6 2 ). Здійснили реконструкцію розподілу діаметрів тривимірних зерен, вирішуючи наведену систему рівнянь, наприклад, за допомогою комп'ютера, знайшли таким чином відносні частки P(Dk), розрахували нормовані значення P'(Dk) з відношення P(Dk ) Pk (D) / n P(Dk ) . У сукупності нормовані k 1 частки P(Dk ) є розподілом розмірів тривимірних зерен в об'ємі. Отримані результати реконструкції наведені в таблиці 6. Таблиця 6 №№ інтервалів k Межі інтервалів Іmin – Imax мкм Розраховані відносні частки P(Dk) 1 2 3 4 5 6 7 8 9 10 0 - 15,6 15,6 - 31,2 31,2 - 46,8 46,8 - 62,4 62,4 - 78,0 78,0 - 93,6 93,6 - 109,2 109,2 - 124,8 124,8 - 140,4 140,4 - 156,0 0 0,0002562 0,0034519 0,0080690 0,0045595 0,0030213 0,0008780 0,0003152 0,0001574 0,0001190 Реконструйовані за пропонованим способом розподіли діаметрів плоских перерізів зерен P'k(d) і діаметрів тривимірних зерен P'(Dk), а також вихідний розподіл довжин хорд Pk(l) додатково представлені графічно (Фіг. 6). Розподіл діаметрів тривимірних зерен в об'ємі (нормовані відносні частки) 0 0,0123003 0,1657365 0,3874205 0,2189163 0,1450612 0,0421574 0,0151361 0,0075585 0,0057132 На заключному етапі виконали розрахунок усіх параметрів для сукупностей тривимірних зерен, їх плоских і лінійних перерізів. Усі результати представлені в таблиці 7. 23 97453 24 Таблиця 7 Об'єкт аналізу Параметри структури Розподіл хорд Pk(l) Загальна кількість заміряних хорд, шт. Середній розмір хорди, мкм Середньоквадратичне відхилення від середнього розміру хорд, мкм Коефіцієнт варіації розподілу розмірів хорд Модальний розмір хорд, мкм Кількість хорд на 1 мм Розподіл плоских Середній діаметр плоских перерізів зерен, мкм перерізів зерен Середньоквадратичне відхилення від середнього діаметра, мкм Pk(d) Коефіцієнт варіації розподілу діаметрів плоских перерізів зерен Модальний розмір діаметрів плоских перерізів, мкм 2 Кількість плоских перерізів зерен на 1 мм Розподіл зерен в Середній діаметр зерен в об'ємі об'ємі P(Dk) Середньоквадратичне відхилення від середнього діаметра, мкм Коефіцієнт варіації розподілу діаметрів зерен в об'ємі Модальний діаметр зерен, мкм Максимальний діаметр зерен, мкм Кількість зерен в 1 мм Номер зерна за стандартом ГОСТ 5639 Використання способу найближчого з аналогів на тому ж плоскому перерізі зеренної структури (шліфі) призвело до отримання середнього діаметра тривимірних зерен Dcp = 55,07 мкм і середнього діаметра плоских перерізів зерен dcp=48,4 мкм, що за ГОСТ 5639 відповідає номеру 6 і свідчить про явну похибку способу. Точність пропонованого способу визначення параметрів структури у порівнянні з найближчим з аналогів підвищилася в декілька разів, оскільки при реконструкції за двома наведеними системами рівнянь виду (7) і (2) врахована багатокутна форма плоских перерізів зерен за рахунок застосування визначених коефіцієнтів форми k і врахована саме реальна поліедрична форма тривимірних зерен за рахунок застосування визначених коефіцієнтів форми k . Крім того, точність пропонованого способу вища через урахування визначеної пропорційної залежності вірогідності потрапляння плоских перерізів зерен на січну лінію і самих об'ємних зерен на січну площину від розмірів, відповідно, плоских перерізів і зерен. За необхідності застосування для аналізу структури рівномірної розмірної шкали з будьякою іншою кількістю інтервалів, розподіл довжин хорд Рk(l)ср, отриманих від статистично необхідної кількості типових плоских перерізів зерен для шкали, в даному випадку, з 10-ма інтервалами, представляють у графічному вигляді (Фіг. 7), шкала при цьому застосовується у відносному вигляді як: l1 / lmax ;l2 / lmax ;...lk / lmax ;...lmax / lmax ; долі в цих же осях координат будують відповідний графік розподілу відносних довжин хорд від кола Pk (l)кола , які розраховують за формулою Значення параметрів 5815 50,71 24,70 48,71 46,8 20 56,77 24,23 42,67 46,8 395 71,41 20,319 28,45 62,4 156 5244 5 2 2 Pk (l)кола dk lk 1 , і потім розраховують кое фіцієнти форми плоских перерізів зерен k для рівномірної шкали з необхідною кількістю розмірних інтервалів за формулою k Pk (l)cp / Pk (l)кола , знаходячи необхідні значення Pk (l)cр і Pk (l)кола безпосередньо з побудованих графіків. Далі аналогічним чином знаходять коефіцієнти форми тривимірних зерен k , для чого розподіл довжин хорд Pk (l)cр , отриманих від статистично необхідної кількості типових за формою максимальних плоских перерізів зерен для рівномірної шкали, в даному випадку, з 10-ма розмірними інтервалами, представляють у графічному вигляді, шкала при цьому застосовується у відносному вигляді як: l1 / lmax ;l2 / lmax ;...lk / lmax ;...lmax / lmax ; в цих же осях координат будують відповідний графік розподілу відносних часток діаметрів кругів від сфери, які розраховують за формулою 2 2 Pk (d)сфери Dk dk 1 , і потім розраховують коефіцієнти форми k для рівномірної шкали з необхідною кількістю розмірних інтервалів за формулою k Pk (l)cp / Pk (d)сфери , знаходячи необхідні значення Pk (l)cр і Pk (d)сфери безпосередньо з побудованих графіків. Крім того, значне розширення технологічних можливостей пропонованого способу обумовлене й тим, що він може бути застосований і до визначення основних параметрів структури із складовими сферичної форми (в цьому випадку коефіцієнти форми k і k в рівняннях (7) і (2) 25 дорівнюють одиниці), а також елементів структури поліедричної, сферичної, еліпсоїдної та подібних їм форм, в тому числі неметалевих включень, графітної і цементитної фаз, вторинних фаз, інтерметалевих фаз та ін., в цьому випадку видимим зображенням структури є зображення плоских перерізів цих елементів структури на шліфі. Таким чином застосування пропонованого способу в порівнянні з найближчим з аналогів 97453 26 дозволяє підвищити точність при одночасному розширенні технологічних можливостей способу визначення основних параметрів об'ємної структури металевих матеріалів, що збільшує круг його практичного застосування, наприклад, при вивченні впливу параметрів структури на властивості цих матеріалів, при розробці технологічних процесів виготовлення металевих виробів, способів і режимів їх термічної обробки. 27 97453 28 29 Комп’ютерна верстка Д. Шеверун 97453 Підписне 30 Тираж 23 прим. Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601
ДивитисяДодаткова інформація
Назва патенту англійськоюMethod for determination of main parameters of three-dimensional structure of metal materials
Автори англійськоюDanilenko Tetiana Petrivna, Danilenko Eduard Ivanovych
Назва патенту російськоюСпособ определения основных параметров объемной структуры металлических материалов
Автори російськоюДаниленко Татьяна Петровна, Даниленко Эдуард Иванович
МПК / Мітки
МПК: G01N 21/00, G01N 33/20
Мітки: спосіб, параметрів, структури, об'ємної, матеріалів, металевих, визначення, основних
Код посилання
<a href="https://ua.patents.su/15-97453-sposib-viznachennya-osnovnikh-parametriv-obehmno-strukturi-metalevikh-materialiv.html" target="_blank" rel="follow" title="База патентів України">Спосіб визначення основних параметрів об’ємної структури металевих матеріалів</a>
Попередній патент: Монета
Наступний патент: Автоматизована електродугова наплавна установка
Випадковий патент: Спосіб виготовлення паркетних елементів












