Спосіб визначення прогнозованого положення балістичних об’єктів

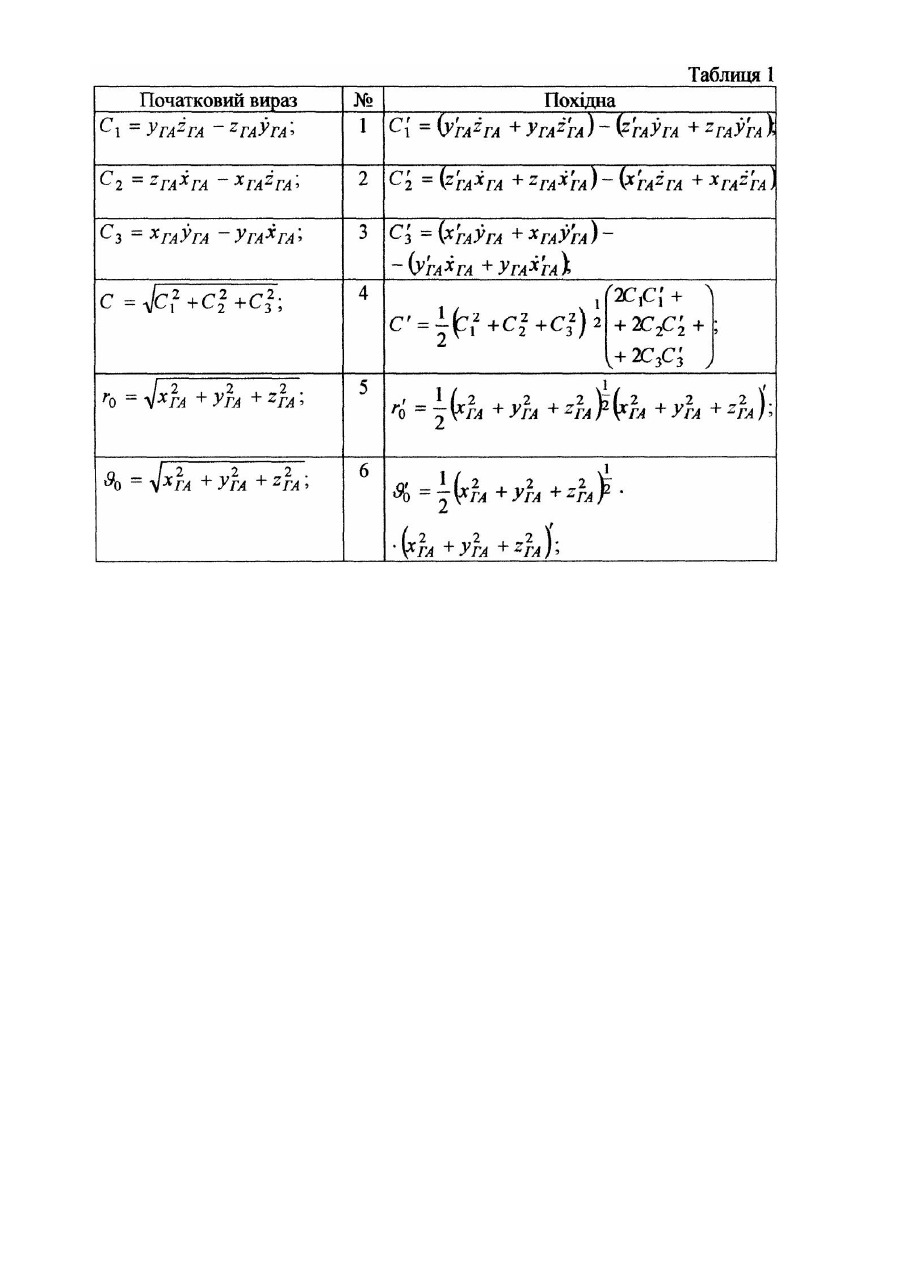
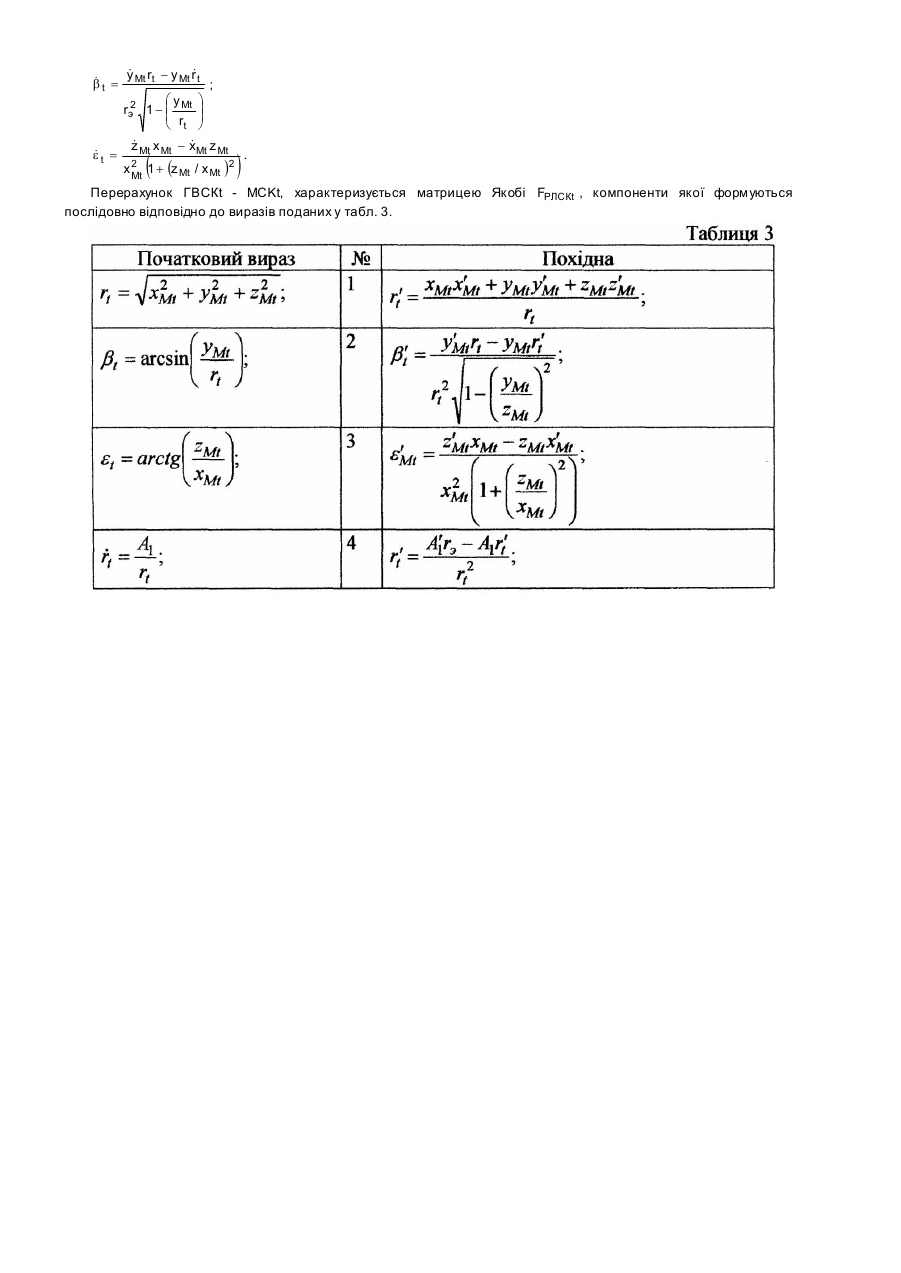
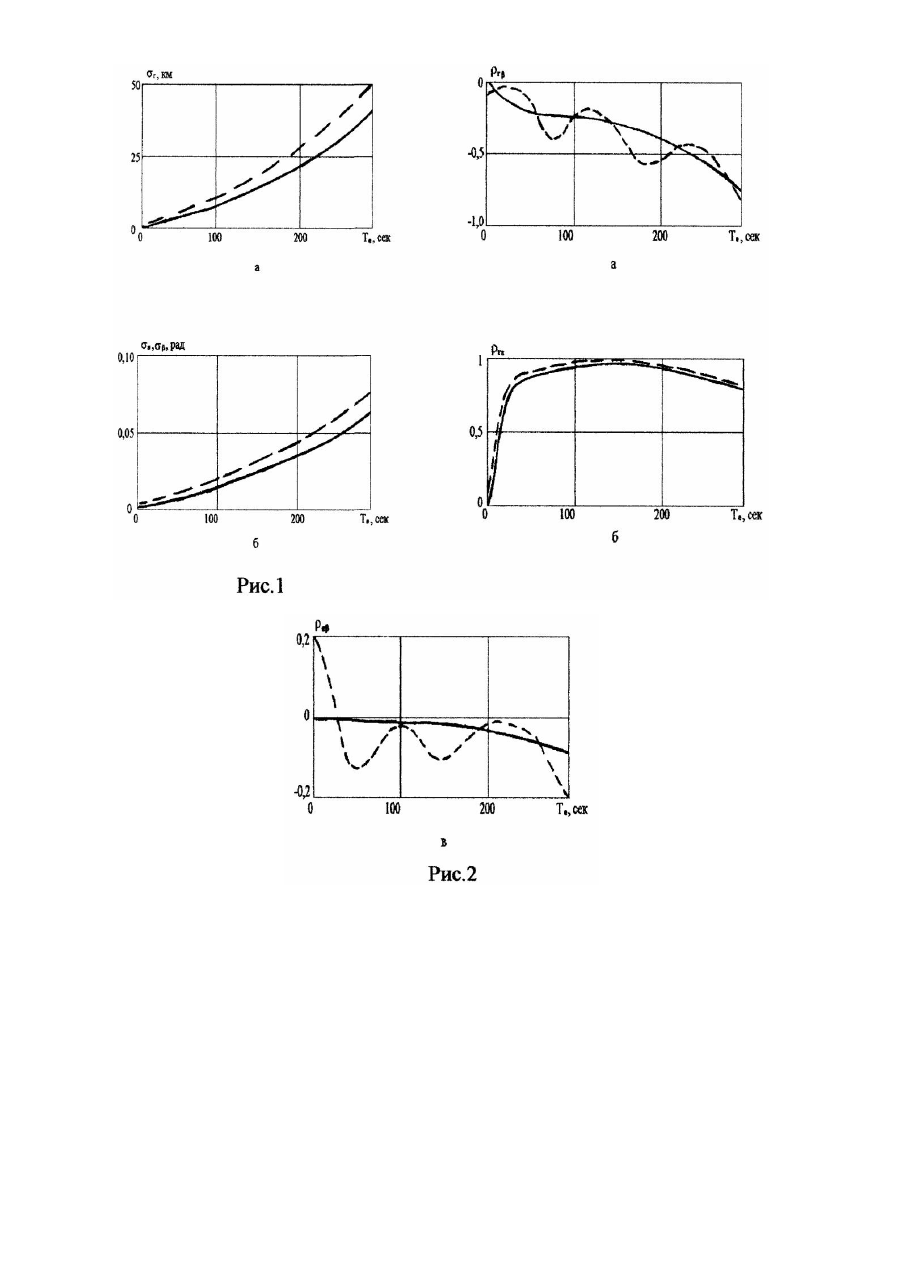
Винахід відноситься до галузі радіолокація, зокрема до радіолокаційних систем, а саме до способів обробки даних. Розрахунок прогнозованого положення балістичного об'єкта (БО) здійснюється за результатами оцінки поточного положення цілі, отриманого на етапі супроводу об'єкта спостереження радіолокаційною станцією (РЛС). Поточне положення БО для РЛС характеризується вектором параметрів у радіолокаційній системі координат (РЛСК) r T &&& (1) d = r ebr eb , де r - відстань до об'єкта; e - кут місця; b - азимут; & , e , b - швидкості зміни відповідних параметрів. Для r & & екстраполяції координат БО на заданий момент часу здійснюють перехід від пунктової системи координат (від r компонент вектора d ) до більш інформативних для стороннього спостерігача вектора параметрів в орбітальній системі координат (ОСК) r T (2) b = a eiW w t , де a - велика піввісь еліпса орбіти; e - ексцентриситет; i - нахилення орбіти; W - довгота висхідного вузла; w - аргумент перигею; t - час проходження БО через перицентр орбіти. Для визначення прогнозованого положення цілі відносно РЛС екстрапольовані координати БО в ОСК перераховують до пунктової системи координат, тобто отримують вектор екстрапольованих параметрів r T & & & (3) dt = rt e t b t rt e t b t . r r r Перерахунки векторів d ® b ® dt - здійснюються з використанням допоміжних систем координат за такою схемою: РЛСК ® місцева система координат (МСК) ® геоцентрична відносна система координат (ГВСК) ® геоцентрична абсолютна система координат (ГАСК) ® ОСК та знов у РЛСК на заданий час екстраполяції. Екстраполяція координат здійснюється, як правило, з використанням рівняння Кеплера в ОСК. r Похибки оцінки поточного положення цілі (компонент вектора d ) обумовлюють появу випадкових похибок r екстраполяції (похибок розрахунку компонент вектора dt ), що спонукає розглядати не точку, а просторову область (строб) можливого знаходження БО на екстрапольований момент часу. Вихідною інформацією для побудови просторового строба є кореляційна матриця похибок екстраполяції (КМПЕ) координат БО загального виду 2 srt r Rbt r rt et r rtb t = r etrt s 2t e r et bt , r btrt r bt et s 2t b (4) 2 де s rt , s 2t , s 2t , - дисперсії визначення екстрапольованих координат дальності, азимута і кута місця БО e b відповідно; r rt et = r etrt , r rt bt = r b trt , r etb t = r bt et - коефіцієнти коваріації відповідних екстрапольованих параметрів траєкторії БО. В подальшому пошук БО на момент екстраполяції реалізується шляхом сканування діаграмою спрямованості РЛС визначеного за матрицею (4) просторового строба. Найбільш близьким способом, обраним за прототип, є спосіб розрахунку екстрапольованих параметрів руху цілі з побудовою строба за похибками визначення екстрапольованих координат, який полягає у тому, що при визначенні екстрапольованого положення цілі просторовий строб будується за кореляційною матрицею похибок екстраполяції, яка визначена без урахування перетворень вихідної кореляційної матриці похибок визначення координат цілі у проміжні системи координат і числового розв'язку рівняння Кеплера, що обумовлює її діагональний вид /1/. r Rbt s2 rt = 0 0 0 s 2t e 0 0 0 , s 2t b (5) Недоліками відомого способу розрахунку екстрапольованих параметрів руху цілі з побудовою строба за похибками визначення екстрапольованих координат, обраного за прототип, є збільшення розмірів просторового стробу можливого знаходження БО на момент екстраполяції, обумовлене нульовими значеннями позадіагональних елементів в матриці (5), і, як наслідок, збільшення часових та енергетичних витрат на пошук балістичного об'єкта за допомогою радіолокаційної станції. В основу винаходу поставлено задачу знизити часові та енергетичні витрати в радіолокаційній станції на пошук балістичного об'єкта шляхом зменшення розмірів просторового строба. Суть винаходу в способі визначення прогнозованого положення балістичних об'єктів, який полягає в розрахунку, відносно радіолокаційної станції, прогнозованих координат балістичного об'єкта на заданий момент часу за результатами оцінки поточного положення об’єкта, а також просторової області похибок прогнозу, яка визначається елементами кореляційної матриці похибок екстраполяції, при якому розрахунок кореляційної матриці похибок екстраполяції здійснюється з урахуванням перетворень вихідної кореляційної матриці похибок визначення координат цілі у проміжні системи координат і числового розв'язку рівняння Кеплера. Порівняльний аналіз способу, який заявляється, із прототипом показує, що спосіб визначення прогнозованого положення балістичних об'єктів відрізняється тим, що розрахунок кореляційної матриці похибок екстраполяції здійснюється з урахуванням перетворень вихідної кореляційної матриці похибок визначення координат цілі у проміжні системи координат і числового розв'язку рівняння Кеплера. Таким чином, спосіб визначення прогнозованого положення балістичних об'єктів, який заявляється, відповідає критерію винаходу "новизна". Суть способу визначення прогнозованого положення балістичних об'єктів пояснюється наступним чином. Розрахунок екстрапольованих координат БО здійснюється з використанням числового розв'язку рівняння r r r Кеплера з реалізацією перерахунків векторів d ® b ® dt . Вказані операції здійснюються відповідно до виразів, поданих в додатку. Для розрахунку просторової області можливого знаходження БО на заданий час екстраполяції необхідно здійснити аналітичний розрахунок кореляційної матриці похибок визначення прогнозованого положення цілі. Згідно з прототипом аналітичний розрахунок корреляційної матриці похибок екстраполяції положення БО може бути здійснено відповідно до загального виразу r r R Y = FR X F T , (6) r r r де R X - початкова кореляційна матриця похибок визначення компонент вектора X ; R Y - вихідна r r ¶y i кореляційна матриця похибок визначення компонент вектора Y за вектором X ; F = , ( j = 1 ...m , k = 1... n ) ¶x k r r матриця Якобі, що відображує перетворення вхідного вектора параметрів X до вектора параметрів Y ; m і n r r кількість елементів векторів X і Y відповідно; F T - транспонована матриця Якобі. r Позначимо Rb - кореляційну матрицю похибок оцінки (КМПО) поточного положення БО в ОСК. З урахуванням введених позначень і перетворень вектора поточного положення БО при визначенні екстрапольованого положення цілі, а також розв'язку рівняння Кеплера, базовий вираз (6) перетвориться до виду , (7) T r R d t = FРЛСКt R МСКt FРЛСКt , [ [ ] (8) ] T T T де R МСКt = FМСКt FГВСКt FГАСКt R r FГАСКt FГВСКt FМСКt ; RРЛСК b - кореляційна матриця похибок визначення поточного положення БО в РЛСК, яка, як правило, відома і характеризує точність розрахунку елементів вектора b ; RМСКt - кореляційна матриця похибок визначення положення БО в МСК; Fj - матриці Якобі відповідних перетворень FМСК - із РЛСК у МСК, FГВСК - із МСК у ГВСК, FГАСК - із ГВСК у Г АСК, FОСК - із ГАСК в ОСК, FГАСКt - з ОСК у ГАСК, FГВСКt - із ГАСК у ГВСК, FМСКt - із ГBCK у МСК, FРЛСКt - із МСК у РЛСК. Вирази, що дозволяють формувати елементи відповідних матриць Якобі, наведені у додатку. Таким чином, вирази (7) та (8) дозволяють здійснити розрахунок кореляційної матриці похибок екстраполяції з урахуванням перетворень початкових координат цілі у проміжні системи координат і числового розв'язку рівняння Кеплера. Результатом використання виразів (7) та (8) є КМПЕ з ненульовими значеннями коефіцієнтів кореляції екстрапольованих координат БО 2 srt r Rbt = r etrt r btrt r rt et r rtb t s 2t e r et bt , r bt et s 2t b (9) Кореляційна матриця похибок екстраполяції виду (9) використовується для побудови просторового строба можливого знаходження БО на момент екстраполяції. Виходячи із викладеного, заявлений спосіб визначення прогнозованого положення балістичних об'єктів здійснюють наступним чином. 1. За оцінками поточного положення цілі реалізують розрахунок екстрапольованого вектора координат БО r r r відповідно до рівняння Кеплеру і перерахунку векторів d ® b ® dt (див. вирази додатку). 2. Згідно з виразами, наведеними у додатку, формують матриці Якобі Fj відповідних перетворень. 3. Реалізують розрахунок кореляційної матриці похибок екстраполяції положення балістичного об'єкта вигляду (9) з урахуванням перетворень вихідної кореляційної матриці похибок визначення координат цілі у проміжні системи і числового розв'язку рівняння Кеплера згідно з виразами (7) та (8). 4. Здійснюють побудову просторового строба можливого знаходження БО на момент екстраполяції за елементами матриці (9). Використання запропонованого способу пояснюється графіками рис. 1, 2. Наведені графіки дозволяють оцінити адекватність розрахунку елементів матриці (9) за виразами (7), (8) і пояснити позитивний ефект від його використання. Як еталон використано числовий метод розрахунку КМПЕ, заснований на проведенні статистичних випробувань із використанням математичного моделювання на ЕОМ. Слід зазначити, що числовий метод розрахунку КМПЕ є досить точним, однак застосувати його в реальних умовах функціонування РЛС неможливо. На рис. 1 подано зміну середньоквадратичного відхилення (СКВ) похибок екстраполяції (значення r r діагональних елементів матриці (9)) s p ( p - елементи вектора d - dt ) при збільшенні часу екстраполяції Te . Суцільній лінії відповідають оцінки СКВ параметрів, отримані відповідно до виразів (7), (8), пунктирній - отримані числовим методом. r На рис. 2 зображена зміна коефіцієнтів кореляції між компонентами вектора dt - r jk ( j , k - елементи вектора r dt ) при збільшенні часу прогнозу Te . С уцільній лінії відповідають криві, що отримані згідно з виразами (7) і (8), пунктирній - отримані числовим методом. Аналіз наведених залежностей показує, що використання виразів (7), (8) дозволяє адекватно визначати елементи кореляційної матриці похибок екстраполяції (9), про що свідчить збіг динаміки зміни еталонних значень компонент КМПЕ і отриманих згідно з аналітичними виразами (див. рис. 1, 2). При збільшенні інтервалу прогнозу просторовий строб обертається в просторі відносно напрямку на РЛС, про що свідчить характер кривих на рис. 1. Тому врахування зміни орієнтації просторового стробу шля хом визначення компонент матриці (9) дозволяє фактично зменшити його розміри відносно напрямку на РЛС і раціонально здійснювати сканування обмеженого стробом простору, що зменшує час та енергетичні витрати на пошук БО при екстраполяції. Підвищення ефективності застосування способу визначення прогнозованого положення балістичних об'єктів, що заявляється, у порівнянні з прототипом, досягається за рахунок зменшення розмірів просторового строба можливого знаходження цілі на момент прогнозу, яке, в свою чергу, знижує часові та енергетичні витрати в РЛС на пошук БО. Це досягається урахуванням перетворень вихідної кореляційної матриці похибок визначення координат цілі у проміжні системи координат і числового розв'язку рівняння Кеплера при розрахунку КМПЕ. Джерела інформації: 1. С.З. Кузьмин "Основы теории цифровой обработки радиолокационной информации", М., издат. "Сов. Радио", 1974, cтop. 232-240 - прототип. Додаток. 1. Перерахунок координат БО із РЛСК в МСК характеризує перехід: r T r T & y & b = r e b & e b ® x M = x M y M z M x M & M zM , r&& який здійснюється згідно виразів: x M = r cos b cos e ; y M = r sinb ; zM = r cos b sine ; & & & & x M = r cos b cos e - rb sin b cos e - re cos b sin e ; & & & y M = r sinb + rb cos b ; & & & & z = r cos b sin e - rb sinb sin e + re cos b cos . M Перерахунок РЛСК - МСК, характеризується матрицею Якобі FМСК , компоненти якої формуються відповідно до виразів: F11 = cos b cos e ; F21 = sinb ; F31 = cos b cos e ; & & F41 = -b sin b cos e - e cos b sin e ; & F51 = b cos b ; & & F61 = -b sin b sin e + e cos e cos b ; F12 = -r cos b sine ; F22 = 0 ; F32 = r cos b cos e ; & & F42 = -r cos b sin e + rb sin b sin e - r& cos b cos e ; e F52 = 0 ; & & & F62 = r cos b cos e - rb sin b cos e - re cos b sin e ; F13 = - r sinb cos e ; F23 = r cos b ; F33 = -r sinb sine ; & & F43 = -r sinb cos e - rb cos b cos e + r& sinb sine ; e & & F53 = r cos b - rb sinb ; & & & F63 = -r sinb sin e - rb cos b sin e - re sin b cos e ; F15 = 0 ; F25 = 0 ; F35 = 0 ; F45 = -r cos b sine ; F55 = 0 ; F65 = r cos b cos e ; F16 = 0 ; F26 = 0 ; F36 = 0 ; F46 = -r sinb cos e ; F56 = r cos b ; F66 = -r sinb sine . 2. Перерахунок координат БО із МСК в ГВСК характеризує перехід: r r & & & Т x m ® x ГВ = х ГВ у ГВ z ГВ zГВ уГВ хГВ , який здійснюється згідно виразів: хГВ = (- sinL sinA m - cos L sinB cos A m )x m + + (cos L cosB )y m + ; + (- sinL cos A m + cos L sinB sinA m )z m + + (N + h0 )cos L cosB yГВ = (cosL sinA m + sinL sinB cos A m )x m + + (sinL cos B )y m + + (cos L cos A m + sinL sinB sin A m )z m + + (N + h0 sinL cos B) zГВ = (cos B cos A m )x m + sinBy m + [( ) ] + (- cos B sin A m )z m + N 1 - e 2 + h 0 sinB 3 ; ; & & хГВ = (- sinL sinA m - cos L sinB cos A m )x m + &m + + (cos L cosB )y ; & + (- sinL cos A m + cos L sinB sinA m )z m & & yГВ = (cosL sinA m + sinL sinB cos A m )x m + & + (sinL cos B )y m + ; &m + (cos L cos A m + sinL sinB sin A m )z & & zГВ = (cos B cos A m )x m + sin By m + ; &m + (- cos B sin A m )z де L , B , h - геодезична довгота, широта та підвищення вимірювача координат БО над поверхнею Землі; aЗ N= , де а З - велика піввісь Землі; е З - ексцентриситет Землі; е З = a (2 - a ) , a = (а З - bЗ ) / аЗ , де 1 - e 2 sin2 B З bЗ - мала піввісь Землі; A m - геодезичний азимут МСК. Перерахунок МСК - ГВСК, характеризується матрицею Якобі FГВСК , компоненти якої формуються відповідно до виразів: F11 = - sinL sinA m - cos L sinB cos A m ; F12 = cos L cos B ; F13 = - sinL cos A m + cos L sinB sinA m ; F14 = 0 ; F15 = 0 ; F16 = 0 ; F21 = cos L sinA m - sinL sinB cos A m ; F22 = sinL cos B ; F23 = cosL cos A m + sinL sinB sinA m ; F24 = 0 ; F25 = 0 ; F26 = 0 ; F31 = cos B cos A m ; F32 = sinB ; F33 = - cos B sin A m ; F34 = 0 ; F35 = 0 ; F36 = 0 ; F41 = 0 ; F42 = 0 ; F43 = 0 ; F44 = - sinL sin A m - cos L sinB cos A m ; F45 = cosL cos B ; F46 = - sinL cos A ; F51 = 0 ; F52 = 0 ; F53 = 0 ; F54 = cos L sinA m - sinL sinB cos A m ; F55 = sinL cos B ; F56 = cos L cos A m + sinL sinB sinA m ; F61 = 0 ; F62 = 0 ; F63 = 0 ; F64 = cos B cos A m ; F65 = sinB ; F66 = - cos B sinA m . 3. Перерахунок координат БО із ГВСК в ГАСК характеризує перехід: r r Т & xГВ ® хГА = х ГА у ГА z ГА & ГА у ГА z ГА , х & який здійснюється згідно виразів: хГА = cos g × х ГВ - sin g × yГВ ; уГА = sing × х ГВ + cos g × y ГВ ; zГА = z ГВ ; & & & хГА = cos g (хГВ - W 3 у ГВ ) - sin g(уГВ + W 3 хГВ ) ; & & & yГА = sing (х ГВ - W 3 уГВ ) + s cos g(уГВ + W 3 хГВ ) ; & & zГА = z ГВ ; де g = S 0 + W 3 (t - Dt M ) - кут у площині екватора Землі, який відраховується від осі ох ГА до осі охГВ геоцентричної відносної системи координат; S 0 - світовий зоряний час на нуль годин гринвіцького часу дати сеансу спостереження БО; W 3 - кутова швидкість обертання Землі; Dt M - часова поправка для переходу від московського до гринвіцького часу. Перерахунок ГВСК - ГАСК, характеризується матрицею Якобі FГАСК , компоненти якої формуються відповідно до виразів: F11 = cos g ; F12 = - sin g ; F13 = 0 ; F14 = 0 ; F15 = 0 ; F16 = 0 ; F21 = sing ; F22 = cos g ; F23 = 0 ; F24 = 0 ; F25 = 0 ; F26 = 0 ; F31 = 0 ; F32 = 0 ; F33 = 1 ; F34 = 0 ; F35 = 0 ; F36 = 0 ; F41 = -W 3 sing ; F42 = - W 3 cos g ; F43 = 0 ; F44 = cos g ; F45 = - sing ; F46 = 0 ; F51 = W 3 cos g ; F52 = - W 3 sing ; F53 = 0 ; F54 = sing ; F55 = cos g ; F56 = 0 ; F61 = 0 ; F62 = 0 ; F63 = 0 ; F64 = 0 ; F65 = 0 ; F66 = 1 . 4. Перерахунок координат БО із ГАСК в ОСК характеризує перехід: r r T xГА ® b = a e i W w t , який здійснюється згідно виразів: & & C1 = у ГА zГА - zГА уГА ; & & C 2 = zГА x ГА - xГА z ГА ; & & C 3 = x ГА yГА - yГА x ГА ; 2 2 & ГА & 2 & ГА C = C1 + C 2 + C2 ; r0 = х 2 + у 2 + zГА ; J = х 2 + уГА + z 2 ; 2 3 ГА ГА & & & æ х х + y ГА yГА + zГА zГА q 0 = arcsinç ГА ГА ç r0 J 0 è r J2 ö ÷; К= 0 0 ÷ m ø æ C ; e = 1 - К 0 (2 - К 0 ) cos 2 q 0 ; W = arctgç - 1 ç C 2 è æ К cos 2 q - 1 ö æC ö 0 ÷ i = arccosç 3 ÷ ; J = arccosç 0 ç C ÷ ç ÷ e è ø è ø a= r0 2 - К0 ö ÷ ÷ ø æ 1- e J ö æ z ö u = arcsinç ГА ÷ ; E = 2arctgç tg ÷ ; ç r sini ÷ ç 1+ e 2 ÷ è 0 ø è ø m E - e sinE ; t= t; l a де m - коефіцієнт рівний добутку гравітаційної сталої на масу Землі; u - аргумент широти; E - ексцентрична w =u-J; l = 32 аномалія; M - середня аномалія; t - поточний час спостереження БО; J - дійсна аномалія. Перерахунок ГАСК - ОСК, характеризується матрицею Якобі FОСК , компоненти якої формуються відповідно до виразів поданих у табл. 1. Отримання за табл. 1 кінцевих значень для формування відповідних елементів матриці FОСК слід здійснювати послідовно, приймаючи одиничним значення параметрів за якими здійснюється r часткове диференціювання і нульовим інші параметри початкового вектора хГА , за умови позначення їх штрихом у виразах. 5. Перерахунок із ОСК до екстрапольованих координат БО в Г АСК - Г ACKt характеризує перехід: r r T & & b ® хГАt = хГАt y ГАt z ГАt хГАt & ГАt z ГАt , y який здійснюється згідно виразів: M= m a 3 (Te - t ) ; Te - час екстраполяції; Ei +1 = M + e sinE i E1 = M ; ітераційне рівняння Кеплера; æ 1+ e E ö J = 2arctgç tg ÷ ; ç 1- e 2 ÷ è ø p 2 p = a (1 - e ) ; r = ; u = w + J ; p - фокальний параметр; 1 + e cos J Vr = m e sinJ ; Vu = p m (1 + e cos J) ; p xГАt = r (cos W cos u - sinW sinu cos i) ; yГАt = r (sinW cos u + cos W sinu cos i) ; zГАt = r sinu sini ; & xГАt = Vr (cos W cos u - sin W sinu cos i) - Vu (cos W sinu + sin W cos u cos i ) & yГАt = Vr (sin W cos u + cos W sinu cos i) - Vu (sin W sin u - cos W cos u cos i ) & zГАt = Vr sinu sini + Vu cos u sini ; ; Перерахунок OCK - ГACKt, характеризується матрицею Якобі FГАСКt , компоненти якої формуються послідовно відповідно до виразів поданих у табл. 2. 6. Перерахунок із ГАСКt до екстрапольованих координат БО в ГВСК - ГВСКt характеризує перехід: r r T & & & xГАt ® x ГBt = x ГBt y ГBt zГBt x ГBt y ГBt zГBt , який здійснюється згідно виразів: хГBt = cos g × х ГAt + sin g × yГAt ; уГBt = - sing × х ГAt + cos g × y ГAt ; zГBt = z ГAt ; & & & хГBt = cos g × х ГAt + sing × y ГAt + W 3 y ГAt ; & ГBt = - sing × х ГAt + cos g × y ГAt - W 3 х ГAt ; & & у & ГBt = z ГAt . & z Перерахунок ГACKt - ГВСКt , характеризується матрицею Якобі FГВСКt , компоненти якої формуються відповідно до виразів: F11 = cos g ; F21 = - sing ; F31 = 0 ; F41 = 0 ; F51 = 0 ; F61 = 0 ; F12 = sing ; F22 = cos g ; F32 = 0 ; F42 = 0 ; F52 = 0 ; F62 = 0 ; F13 = 0 ; F23 = 0 ; F33 = 1 ; F43 = 1; F53 = 1 ; F63 = 1 ; F14 = 1 ; F24 = 0 ; F34 = 0 ; F44 = cos l ; F54 = - sing ; F64 = 0 ; F15 = 0 ; F25 = 0 ; F35 = 0 ; F45 = sing ; F55 = cos g ; F65 = 0 ; F16 = 0 ; F26 = 0 ; F36 = 0 ; F46 = 0 ; F56 = 0 ; F66 = 1 . 7. Перерахунок із ГВСКt до екстрапольованих координат БО в МСК - MCKt характеризує перехід:, r r & & & T xГВt ® x Mt = x Mt y Mt z Mt x Mt y Mt z Mt , який здійснюється згідно виразів x Mt х ГВt - (N + h0 )cos L cosB y Mt y ГВt - (N + h0 ) sinL cos B r z Mt zГВt - N1 - e2 + h0 sinB -1 3 x Mt = = A ГВМ ; & & x Mt x Mt & & y Mt y Mt & & z Mt z Mt (( - sinL sin A m A ¶ мМ = cos L sinB cos A m cos L sin A m - sinL sinB cos A m cosB cos A m ) ) cos L cos B sinL cos B sin B - sinL cos A m + + cos L sinB sin A m cos L cos A m + + sinL sinB sin A m - cos B sin A m . Перерахунок ГВСКt - MCKt, характеризується матрицею Якобі FМСКt , компоненти якої формуються відповідно до виразів: -1 F11 = A ГВМ11 ; -1 F21 = AГВМ21 ; -1 F31 = A ГВМ31 ; F41 = 0 ; F51 = 0 ; F61 = 0 ; -1 F12 = A ГВМ12 ; -1 F22 = A ГВМ22 ; F32 = A - 1 32 ; ГВМ F42 = 0 ; F52 = 0 ; F62 = 0 ; -1 F13 = A ГВМ13 ; -1 F23 = A ГВМ23 ; -1 F33 = A ГВМ33 ; F43 = 0 ; F53 = 0 ; F63 = 0 ; F14 = 0 ; F24 = 0 ; F34 = 0 ; -1 F44 = A ГВМ11 ; -1 F54 = A ГВМ21 ; -1 F64 = A ГВМ31 ; F15 = 0 ; F25 = 0 ; F35 = 0 ; -1 F45 = A ГВМ12 ; -1 F55 = A ГВМ22 ; -1 F65 = A ГВМ32 ; F16 = 0 ; F26 = 0 ; F36 = 0 ; -1 F46 = A ГВМ13 ; -1 F56 = A ГВМ23 ; -1 F66 = A ГВМ33 . Величини, що входять до складу виразів для перерахунку ГВСКt - MCKt мають сенс аналогічних параметрів перерахунку МСК - ГОСК. 8. Перерахунок із MCKt до екстрапольованих координат БО в РЛСК - PJICKt характеризує перехід: r r T & & & x Mt ® b t = rt e t b t rt e t b t , який здійснюється згідно виразів: 2 rt = x Mt + y 2 + z 2 ; Mt Mt æy ö b t = arcsinç Mt ÷ ; çr ÷ è Mt ø æz ö e t = arctgç Mt ÷ ; çx ÷ è Mt ø &t = r & & & x Mt x Mt + y Mt y Mt + zMt z Mt rt ; & & y r - y Mt r t & b t = Mt t ; æ y Mt ö 2 rэ 1 - ç ç r ÷ ÷ è t ø & & z Mt x Mt - xMt z Mt & et = . 2 x Mt 1 + (z Mt / x Mt )2 ( ) Перерахунок ГВСКt - MCKt, характеризується матрицею Якобі FРЛСКt , компоненти якої формуються послідовно відповідно до виразів поданих у табл. 3.