Спосіб виконання арифметичних операцій в обчислювальних системах
Номер патенту: 83035
Опубліковано: 10.06.2008
Автори: Тверезовська Юлія Василівна, Тверезовський Василь Семенович
Формула / Реферат
Спосіб виконання арифметичних операцій в обчислювальних системах, при якому кодові дані подають на вхідні регістри, виконують арифметично-логічні операції і результат подають на вихідний регістр, який відрізняється тим, що кодові дані з вхідних регістрів подають на входи сумісного повного дешифратора, яким перетворюють р-розрядний сумісний двійковий код вхідних двох регістрів на всі його сполучення в k-розрядний одиничний код, де p=m+n, k=2p, m і n - кількість розрядів вхідних двох регістрів, в які заносять вхідні дані для виконання арифметичних операцій множення, ділення, додавання і віднімання, повний сумісний дешифратор визначають за системою булівських функцій (1)
 (1),
(1),
також використовують чотири шифратори, які програмують для виконання арифметичних операцій - множення, ділення, додавання і віднімання, при програмуванні шифратора для множення визначають добутки Α1, Α2, А3,..., Ak-2, Ak-1, Ak кожних комбінацій двох чисел, що описують системою функцій (2)
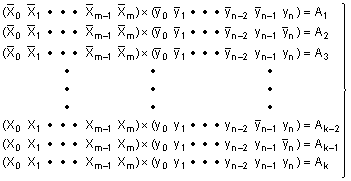 (2),
(2),
і заносять добутки в шифратор по адресах відповідно системі функцій (1) – Z1, Z2, Z3, ..., Zk-2, Zk-1, Zk, при програмуванні шифратора для ділення визначають частки від ділення В1, В2, В3,..., Bk-2, Bk-1, Bk кожних комбінацій двох чисел, що описують системою функцій (3)
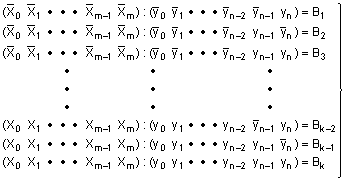 (3),
(3),
і заносять частки в шифратор по адресах відповідно системі функцій Ζ1, Ζ2, Z3, ..., Zk-2, Zk-1, Zk, при програмуванні шифратора для виконання операції додавання визначають суми від додавання С1, С2, С3, ..., Ck-2, Ck-1, Ck кожних комбінацій двох чисел, що описують системою функцій (4)
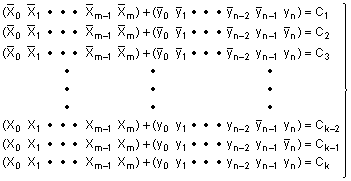 (4),
(4),
і заносять суми в шифратор по адресах відповідно системі функцій (1) Ζ1, Z2, Z3, ..., Zk-2, Zk-1, Zk, при програмуванні шифратора для виконання операції віднімання визначають різниці віднімання D1, D2, D3,..., Dk-2, Dk-1, Dk кожних комбінацій двох чисел, що описують системою функцій (5)
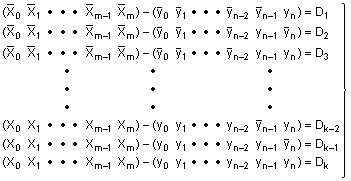 (5),
(5),
і заносять різниці в шифратор по адресах відповідно системі функцій (1) Z1, Z2, Z3, ..., Zk-2, Zk-1, Zk, при виконанні арифметичних операцій відповідні вихідні одиничні коди дешифратора, що описують системою булівських функцій (1), комутують з входами відповідних шифраторів, що описують системою функцій (2), ..., (5), і зчитують з відповідних виходів шифраторів результати виконання арифметичних операцій, які заносять в вихідний регістр.
Текст
Спосіб виконання арифметичних операцій в обчислювальних системах, при якому кодові дані подають на вхідні регістри, виконують арифметично-логічні операції і результат подають на вихідний регістр, який відрізняється тим, що кодові дані з вхідних регістрів подають на входи сумісного повного дешифратора, яким перетворюють ррозрядний сумісний двійковий код вхідних двох регістрів на всі його сполучення в k-розрядний одиничний код, де p=m+n, k=2p, m і n - кількість розрядів вхідних двох регістрів, в які заносять вхідні дані для виконання арифметичних операцій множення, ділення, додавання і віднімання, повний сумісний дешифратор визначають за системою булівських функцій (1) yn ) = C1 yn ) = C2 yn ) = C3 (4), 3 83035 і заносять суми в шифратор по адресах відповідно системі функцій (1) Ζ1, Z2, Z3, ..., Zk-2, Zk-1, Zk, при програмуванні шифратора для виконання операції віднімання визначають різниці віднімання D1, D2, D3,..., Dk-2, Dk-1, Dk кожних комбінацій двох чисел, що описують системою функцій (5) ü ï ï ï yn -1 yn ) = D3 ï ï · ï ï · · · ý ï · · · ï ( X0 X1 · · · Xm -1 Xm ) - ( y0 y1 · · · yn - 2 yn -1 yn ) = Dk - 2 ï ï ( X0 X1 · · · Xm -1 Xm ) - ( y0 y1 · · · yn - 2 yn -1 yn ) = Dk -1 ï ( X0 X1 · · · Xm -1 Xm ) - ( y0 y1 · · · yn - 2 yn -1 yn ) = Dk ï ï þ ( X0 X1 · · · Xm -1 Xm ) - ( y0 ( X0 X1 · · · Xm -1 Xm ) - ( y0 ( X0 X1 · · · Xm -1 Xm ) - ( y0 · · y1 · · · yn - 2 y1 · · · yn - 2 y1 · · · yn - 2 yn -1 yn ) = D1 yn -1 yn ) = D2 b5 b4 b3 b2 і заносять різниці в шифратор по адресах відповідно системі функцій (1) Z1, Z2, Z3, ..., Zk-2, Zk-1, Zk, при виконанні арифметичних операцій відповідні вихідні одиничні коди дешифратора, що описують системою булівських функцій (1), комутують з входами відповідних шифраторів, що описують системою функцій (2), ..., (5), і зчитують з відповідних виходів шифраторів результати виконання арифметичних операцій, які заносять в вихідний регістр. (5), Передбачуваний винахід відноситься до обчислювальної техніки і призначений для виконання арифметично-логічних операцій. Відомий спосіб виконання математичних операцій - матричний [див. с. 93 - 94, К.Г. Самофалов, A.M. Романкевич, Β.Η. Валуйский, и др. Прикладная теория цифровых автоматов. К.: "Вища школа", 1987] в якому множене А і множник В поміщають в регістрах ЄОМ, перетворюють їх в часткові добутки, за допомогою суматорів підсумовують часткові добутки, а їх сума є результат множення. Приклад A = a6 a 5 a 4 a3 a 2 a1 ´ B = b6 4 b1 a6b1 a 5b1 a 4b1 a3b1 a 2b1 a1b1 a6b 2 a5b 2 a 4b 2 a3b2 a 2b2 a1b 2 · · · · · · a6b 5 a5b 5 a 4b5 a 3b5 a 2b5 a1b5 a6b 6 a 5b6 a 4b 6 a3b 6 a 2b6 a1b 6 C12 C11 C10 · · · · · C4 C3 C2 C1 Сі=0 або 1, результат множення - дванадцяти розрядне число. Недоліком матричного способу є мала швидкодія при виконанні множення кодових даних із-за одержання часткових добутків і використання суматорів. Відомий спосіб виконання операцій ділення чисел [див. с. 382 - 383. Уильям Столлингс, Структурна організація і архітектура комп'ютерних систем, 5-е издание; Перевод с английского, - Μ.: Издательский дом «Вильямс»,2002.896с.], який полягає в тому, що перед початком виконання операції дільник поміщають в регістр М, ділене в регістр Q, а регістр А очищають, на кожному кроці вміст регістрів А і Q зсовують на один розряд ліворуч, вміст регістра М віднімають з вмісту А, визначається чи ділиться А на М (тобто результат віднімання більший чи менший нуля ), якщо результат позитивний, в молодший розряд часткового Q0, заноситься код 1, в противному разі в молодший розряд часткового заносять код 0, а значення часткового остатку (вміст регістра А ) відновлюється, для чого до нього прибавляють вміст регістра М, після цього зменшується значення в лічильнику циклів, в якому перед початком виконання операції записують число n - кількості елементарних циклів, після завершення n - циклів частне буде знаходитись в регістрі Q, а остаток - в регістрі А. Недоліком даного способу виконання операції ділення є мала його швидкодія, із - за виконання операцій зсуву даних і використання суматорів. Відомий спосіб ділення чисел [див. с. 110-111. К.Г. Самофалов, A.M. Романкевич, Β.Η. Валуйский, и др. Прикладная теория цифровых автоматов. К.: "Вища школа", 1987,375с.] який полягає в тому, що в способі використовують n-розрядний регістр дільника, (n+1 ) - розрядний регістр частки з зсувом ліворуч: n або (n+1) розрядний суматор з зсувом ліворуч і схема керування, суматор виконує зсув текучого залишку ліворуч і алгебраїчне додавання його з дільником, передає в суматор модуля дільника, або його доповнення забезпечують блоком керування діленням, який аналізує зсунені з суматора знакові цифри остачі, ці цифри інвертують і подають в молодший розряд регістра частки, як цифри частки. Недоліком даного способу виконання операції ділення є мала швидкодія, обумовлена виконанням операцій зсуву даних та використанням суматорів. Відомий спосіб виконання арифметичнологічних операцій з кодовими даними який більш близький по своїй суті до запропонованого [див. с. 374. Уильям Столлингс, Структурная организация и архитектура компьютерных систем. Москва. С.Петербург. Киев, 2002] який полягає в тому, що при виконанні операції множення формують часткові добутки, по одному на кожний розряд множника, при цьому кожний черговий частковий добуток зсувають на одну позицію вліво відносно попереднього, затим часткові добутки підсумовують, а їх сума є результат множення, тобто хай 1011´ 1101 , тоді 5 83035 1011 1011 , ü ï ï ï ï ï · · ï ï · · · ý ï · · · ï ( X0 X1 · · · Xm -1 Xm ) + ( y 0 y1 · · · yn - 2 yn- 1 yn ) = Ck - 2 ï ï ( X0 X1 · · · Xm -1 Xm ) + ( y 0 y1 · · · yn - 2 yn- 1 yn ) = Ck - 1 ï ( X0 X1 · · · Xm -1 Xm ) + ( y 0 y1 · · · yn - 2 yn- 1 yn ) = Ck ï ï þ (4), ü ï ï ï ï ï ï ï · · · ý ï · · · ï ( X0 X1 · · · Xm - 1 Xm ) - ( y 0 y1 · · · yn- 2 yn- 1 yn ) = Dk - 2ï ï ( X0 X1 · · · Xm - 1 Xm ) - ( y 0 y1 · · · yn- 2 yn- 1 yn ) = Dk -1 ï ( X0 X1 · · · Xm - 1 Xm ) - ( y 0 y1 · · · yn- 2 yn- 1 yn ) = Dk ï ï þ (5), ( X0 X1 · · · Xm-1 Xm ) : (y 0 y1 · · · y n- 2 yn-1 · · · · 10001111 при цьому, при двох n - розрядних цілих чисел буде 2n - розрядне число. Недоліком способу є мала швидкодія виконання математичних операцій із-за операцій зсуву даних і використання суматорів. Задачею даного технічного рішення є створення к способу виконання математичних операцій, особливості якого забезпечили б можливість виконання арифметично-логічних операцій множення, ділення, додавання, віднімання з більш високою швидкодією. Рішення поставленої задачі досягаються тим, що в способі виконання математичних операцій, при якому виконують арифметично-логічні операції з кодовими даними, наперед будують сумісний повний дешифратор, яким перетворюють ррозрядний сумісний двійковий код вхідних двох регістрів на всі його сполучення в k-розрядний одиничний код, відповідно системі функцій (1), де p=m+n, k=2p, m і m - кількість розрядів вхідних двох регістрів, в які заносять вхідні дані множення, ділення, додавання і віднімання, повний сумісний дешифратор визначають за системою булевих функцій (1), ü ï ï Z1 = X0 X1 X2 · · · Xm -1 Xm y 0 y1 · · · yn- 2 yn- 1 yn ï Z 2 = X 0 X1 X2 · · · Xm- 1 Xm y0 y1 · · · yn- 2 yn- 1 yn ï ï ï · · · ï · · · ï ý · · · ï ï Zk - 3 = X0 X1 X2 · · · Xm- 1 Xm y0 y1 · · · yn- 2 yn- 1 yn ï ï Zk - 2 = X0 X1 X 2 · · · Xm-1 Xm y0 y1 · · · yn - 2 yn -1 yn ï ï Zk -1 = X0 X1 X2 · · · Xm- 1 Xm y0 y1 · · · yn- 2 yn-1 yn ï Zk = X0 X1 X 2 · · · Xm-1 Xm y0 y1 · · · yn - 2 yn -1 yn ï þ Z 0 = X0 X1 X2 · · · Xm -1 Xm y 0 y1 · · · yn - 2 yn -1 yn (1), затим програмують чотири шифратори для виконання арифметичних операцій - множення, ділення, додавання та віднімання, при програмуванні шифратора для множення визначають добутки Α1, Α2, А3,..., Ak-2, Ak-1, Ak кожних комбінацій двох чисел, що описують системою функцій (2) і заносять добутки в шифратор по адресам відповідно системі функцій (1) – Z1, Z2, Z3, ..., Zk-2, Zk-1, Zk, при програмуванні шифратора для ділення визначають частки від ділення В1, В2, В3,..., Bk-2, Bk-1, Bk, кожних комбінацій двох чисел, що описують системою функцій (3) і заносять частки в ü ï ï ï ï ï · ï ï · · · ý ï · · · ï X1 · · · Xm - 1 Xm ) ´ ( y0 y1 · · · yn - 2 yn -1 yn ) = Ak - 2 ï ï X1 · · · Xm - 1 Xm ) ´ ( y0 y1 · · · yn - 2 yn -1 yn ) = Ak -1 ï X1 · · · Xm - 1 Xm ) ´ ( y0 y1 · · · yn - 2 yn -1 yn ) = Ak ï ï þ ( X0 X1 · · · Xm - 1 Xm )´ ( y0 ( X0 X1 · · · Xm - 1 Xm ) ´ ( y0 ( X0 X1 · · · Xm - 1 Xm ) ´ ( y0 · · y1 · · · y1 · · · y1 · · · yn - 2 yn -1 yn ) = A1 yn - 2 yn -1 yn ) = A 2 yn - 2 yn -1 yn ) = A 3 (2), · · · 1011 ( X0 (3), ( X0 X1 · · · Xm-1 Xm ) : (y 0 y1 · · · y n- 2 yn-1 y n ) = B2 0000 1011 ( X0 ( X0 ü ï ï ï y n ) = B3 ï ï ï ï ý ï ï y n ) = Bk - 2 ï ï y n ) = Bk -1 ï y n ) = Bk ï ï þ ( X0 X1 · · · Xm-1 Xm ) : (y 0 y1 · · · y n- 2 yn-1 y n ) = B1 ´ 1101 6 · · ( X0 X1 · · · Xm-1 ( X0 X1 · · · Xm-1 ( X0 X1 · · · Xm -1 Xm ) : (y 0 Xm ) : (y 0 Xm ) : (y 0 y1 · · · y n - 2 y1 · · · y n - 2 y1 · · · y n - 2 yn-1 yn-1 yn-1 ( X0 X1 · · · Xm -1 Xm ) + ( y 0 y1 · · · yn - 2 yn- 1 yn ) = C1 ( X0 X1 · · · Xm -1 ( X0 X1 · · · Xm -1 · Xm ) + ( y 0 Xm ) + ( y 0 y1 · · · yn - 2 y1 · · · yn - 2 yn- 1 yn ) = C2 yn- 1 yn ) = C3 ( X0 X1 · · · Xm- 1 Xm ) - ( y 0 y1 · · · yn- 2 yn- 1 yn ) = D1 ( X0 X1 · · · Xm - 1 Xm ) - ( y 0 y1 · · · yn- 2 yn- 1 yn ) = D2 ( X0 X1 · · · Xm - 1 Xm ) - ( y 0 y1 · · · yn- 2 yn- 1 yn ) = D3 · · · шифратор по адресам відповідно системі функцій (1) Ζ1, Ζ2, Z3, ..., Zk-2, Zk-1, Zk, при програмуванні шифратора для виконання операції додавання визначають суми від додавання С1, С2, С3, ..., Ck-2, Ck-1, Ck, кожних комбінацій двох чисел, що описують системою функцій (4) і заносять суми в шифратор по адресам відповідних системі функцій (1) Ζ1, Z2, Z3, ..., Zk-2, Zk-1, Zk, - при програмуванні шифратора для виконання операції віднімання визначають різниці віднімання D1, D2, D3,..., Dk-2, Dk-1, Dk, кожних комбінацій двох чисел, що описують системою функцій (5) і заносять різниці в шифратор, по адресам відповідно системі функцій (1) Ζ1, Ζ2, Z3, ..., Zk-2, Zk-1, Zk, при виконанні арифметичних операцій відповідні вихідні одиничні коди дешифратора, що описують системою булевих функцій (1), комутують з входами відповідних шифраторів, що описують системою функцій (2), ..., (5), і зчитують з відповідних виходів шифраторів результати виконання арифметичних операцій. Порівнюють швидкодію відомих і запропонованого способів виконання арифметично-логічних операцій на прикладі операції множення, яка забирає значно більше часу других операцій і зустрічається приблизно в 10 раз частіше інших математичних операцій. Для відомого способу згідно прототипу можна записати T1 = n( t1 + t 2 ) , де Т1 - час виконання операції відомого способу; n - кількість розрядів вхідних даних; t1 - час виконання однієї операції зсуву; t2 - час виконання операції одного суматора; 7 83035 наприклад, при n - 12 розрядів і t1 » t2 = t , швидкодія способу T1 = 24t . В запропонованому способі кожна арифметична операція виконується за один такт t , тобто T2 » t £ T1 , де T2 - час виконання операції запропонованого способу. При односходинковому способі побудови дешифратора забезпечують максимальну швидкодію, але вимагають більших витрат устаткування. Мінімальну кількість устаткування забезпечують багатосходинковим дешифратором, тривалість операції дешифрування при цьому зростає пропорційно числу сходинок. Але там, де необхідно мати високу швидкодію, перевагу віддають дешифратору односходинковому, особливо коли обмежені, в деякому інтервалі, розрядності вхідних даних, тоді відпадає необхідність в побудові повного дешифратора і можна обійтись не повним і односходинковим. Комп’ютерна верстка В. Клюкін 8 Для виконання математичних операцій з однією змінною використовують один дешифратор, а шифратори для кожної операції програмують окремо. Для зменшення витрат устаткування при виконанні арифметичних операцій множення і додавання визначають більший (або менший) з співмножників та більший з додатків і заносять їх в один визначений вхідний регістр, також ділене і дільник, від'ємник і віднімач, заносять окремо в визначені вхідні регістри. З приведеного порівняння швидкодії виконання математичної операції слідує, що швидкодія запропонованого способу значно перевищує відомі способи. Таким чином запропонований спосіб виконання арифметичне - логічних операцій забезпечує значно більшу швидкодію що обумовлює його широке промислове застосування в комп'ютерах та інших обчислювальних приладах і системах. Підписне Тираж 26 прим. Міністерство освіти і науки України Державний департамент інтелектуальної власності, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601
ДивитисяДодаткова інформація
Назва патенту англійськоюMethod to perform arithmetic operations in computer systems
Автори англійськоюTverezovskyi Vasyl Semenovych, Tverezonska Yulia Vasylivna
Назва патенту російськоюСпособ исполнения арифметических операций в вычислительных системах
Автори російськоюТверезовский Василий Семенович, Тверезовская Юлия Васильевна
МПК / Мітки
МПК: G06C 15/00, G06F 17/14, G06F 7/00
Мітки: арифметичних, системах, операцій, обчислювальних, спосіб, виконання
Код посилання
<a href="https://ua.patents.su/4-83035-sposib-vikonannya-arifmetichnikh-operacijj-v-obchislyuvalnikh-sistemakh.html" target="_blank" rel="follow" title="База патентів України">Спосіб виконання арифметичних операцій в обчислювальних системах</a>
Попередній патент: Регулятор динамічних навантажень бурильної колони
Наступний патент: Фармацевтична композиція у вигляді гідрогелю для трансдермального введення в організм діючих речовин
Випадковий патент: Теплоакумулююча капсула








