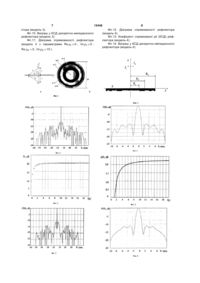
Дискретно-імпедансний рефлектор

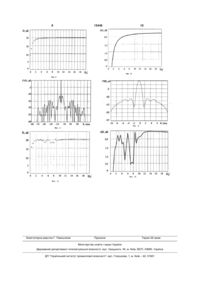
Дискретно-імпедансний рефлектор, що виконаний у вигляді плоскої лінзи Френеля, поверхня якого складається з послідовно пронумерованих зон (парні і непарні зони Френеля), причому в ме жах однієї сукупності зон (наприклад, зони з непарними номерами) є покриття з хорошого провідника, який відрізняється тим, що друга сукупність зон Френеля (зони з парними номерами) також заповнена матеріалом, на поверхні кожної з зон Корисна модель відноситься до антеною техніці. Може бути використане в якості низько профільного рефлектора дзеркальних антен, які застосовуються у техніці наземного й космічного радіозв'язку, радіолокації, у коліматорах і фокусуючих пристроях НВЧ з метою поліпшення рівномірності поля в розкритті антен і коліматорів, підвищення коефіцієнта спрямованої дії й поліпшення фокусування. Більшість антен, що працюють у діапазонах сантиметрових і більш коротких хвиль, ставляться до класу апертурних антен оптичного типу. Це, наприклад, дзеркальні й лінзові антени. Робоча поверхня таких антен не-плоска (наприклад, параболічна, гіперболічна або еліптична), що може створювати певні конструктивні й технологічні незручності. Ідея створення антен із плоскої або майже плоскою робочою поверхнею базується на принципі Гюйгенса-Френеля й понятті зон Френеля. Класичний низько профільний рефлектор може бути виконаний у вигляді дискретної поверхні так званої «зонної пластинки» [1,2,3] інакше називаної лінзою Френеля. Лінза Френеля утворюється шляхом розбиття уявної (утворюючої) плоскої поверхні S на зони Френеля [4] з подальшим заповненням або парних, або непарних зон добре провідним матеріалом. До переваг рефлекторів у вигляді дискретноплоскої поверхні (типу лінзи Френеля) можна віднести високу технологічність виготовлення й можливість зборки робочої поверхні великого розміру з окремих плоских сегментів; зниження негативного впливу теплових і механічних деформацій; зменшення впливу опадів, що заважають (налипання снігу, скупчення вологи на дзеркалі), зниження ефектів деполяризації й інші. Проте така дискретна поверхня є багато фокусною: вона має властивості, як лінзи, так і рефлектора. Тобто вона має направлені властивості як «на просвіт», так й «на відбиття», що є її істотним недоліком. Пропонована корисна модель поліпшує направлені властивості дискретної поверхні за рахунок усунення в ній ознак і властивостей лінзи й поліпшення за рахунок цього спрямованих властивостей рефлектора. Нагадаємо, що принцип розбиття плоскої поверхні, на зони Френеля (Фіг.1) забезпечується виконанням умови: rn f n / 2, де: n - номер зони (нумерація зон позначена на фіг.1 б), rn - відстань від джерела до зовнішнього краю n -ї зони, f- фокусна відстань, - довжина хвилі. При цьому різниця фаз полів створюваних джерелом монохроматичної електромагнітної хвилі в крайніх точках кожної зони становить 180°; Радіуси зон Френеля Rn визначаються співвідношенням: 2 2 zn xn 2fn / 2 (n / 2)2 (1) Заповнюючи тонким провідним шаром зони, що мають парні номери, і залишаючи незаповненими зони, що мають непарні номери, (або навпаки), утворимо лінзу Френеля -поверхню, яка складається з тонких кільцевих добре провідних зон, що чергуються з незаповненими зонами, та має (13) 15446 (11) UA (19) Rn U відношення дотичних складових векторів i і i (поверхневий імпеданс) за абсолютною величиною у декілька разів перевищує хвильовий опір вільного простору. 3 15446 4 властивості, як лінзи, так і рефлектора (дзеркала). одержуваний у випадку дискретно-імпедансного При осьовому опроміненні такої дискретної рефлектора. поверхні плоскою хвилею, наприклад, що прихоПомістимо у фокальній області сторонні джедить із позитивного напряму осі z, розсіяне поле рела - L ниток магнітного струму паралельних осі x фокусується не тільки в двох ближніх фокальних с точках F1 і F2, але також й у нескінченно вилучених амплітудою /,, / = \,...L. точках z на оптичній осі. Тоді густина поверхневого струму j(y, ( y ) ), Аналогічно цьому, при опромінюванні лінзи задовольняє рівнянню [5] L Френеля джерелом сферичної хвилі, наприклад, (2) ( 2) 0 0 J y, y y' J y' , y' H( 2) k y y' dy' k y y IH 0 що знаходиться на оптичній осі в точці z=f, розсія2 S 2  1 0 не поле також фокусується не тільки в нескінченно де H( 2 ) ( y ) - функція Ганкеля другого роду, 0 віддалених точках z на оптичній осі, але також і в двох ближніх фокальних точках F1 й F2 k a a - хвильове число верхнього напівпросОтже, при практичній реалізації плоских лінз тору. Френеля як елементів антенних або фокусуючих У формулі (2) інтегрування здійснюється в мепристроїв (лінз або рефлекторів) виявляється влажах всієї нескінченної площини S. Для того, щоб стивий їм недолік: більше половини енергії падаюдосліджувати властивості дискретно-імпедансного чого поля використовується не за призначенням, рефлектора кінцевих розмірів припустимо, що рощо, зокрема, є причиною зниження коефіцієнта зподіл амплітуд струмів джерел підкоряється бінаправленої дії D антен з таким рефлектором. номіальному закону. Поставлена задача різкого зниження рівня заЯк добре відомо, у цьому випадку діаграма дніх бічних пелюстків діаграми спрямованості дисспрямованості системи джерел не має бічних пекретної поверхні й збільшення коефіцієнта напралюсток [6] і, при певному виборі фокусної відстані вленої дії антени з рефлектором у вигляді такої (у процесі дискретизації поверхні), кількості джеповерхні. Пропонована конструкція, називана дисрел і відстані між ними, опромінюватися буде тількретно-імпедансним рефлектором має геометрію ки кінцева ділянка дискретної поверхні AS. За меподібну до лінзи Френеля, а саме, як й у прототижами області AS амплітуди поверхневих струмів пу, уявлювана площина також дискретизується будуть нехтовно малі. Отже, в (2) можна обмежи(розбивається на зони Френеля). Технічним розтися інтегруванням у межах цієї області, вважаюв'язанням поставленої задачі є заповнення всіх чи, що її розміри відповідають розміру апертури без винятку зон Френеля таким матеріалом, щоб у досліджуваного рефлектора. Тоді вирішуючи рівмежах кожної зони забезпечувалося певне знаняння чення поверхневого імпедансу. Це може бути, наL (3) ( 2) 0 0 приклад, тонкий одношаровий або багатошаровий J y, y y' J y' , y' H( 2) k y y' dy' k y y IH 0 2 S 2  1 0 металевий, металізований магнітний або діелектможна визначити розподіл поверхневих струричний матеріал з металевими вкрапленнями і мів у межах апертури AS дискретно-імпедансного (або) отворами різної форми, штирями або канаврефлектора й потім, шляхом, чисельного інтегруками [5,6]. вання розрахувати розподіл розсіяного поля в даДля обґрунтування запропонованого розв'яльній зоні, побудувати діаграму спрямованості й зання поставленої задачі був проведений чисельдалі розрахувати коефіцієнт направленої дії. ний експеримент, заснований на розв'язанні елекПоставлена задача розв'язується методом тродинамічної задачі про знаходження поля, Крилова - Боголюбова [5] стосовно до інтегральнорозсіяного дискретно-імпедансною поверхнею, при го рівняння для густини електричного поверхневоопромінюванні джерелом електромагнітного поля. го струму. При цьому інтегральне рівняння (3) звоЗ цією метою розглядалася наступна модельдиться до системи лінійних алгебраїчних рівнянь, на двовимірна (геометрія рефлектора й характешляхом чисельного розв'язання якої й знаходитьристики електромагнітного поля не залежать від ся розподіл щільності поверхневого струму. Потім координати z) задача. знайдені розподіли поверхневого струму викорисНехай є нескінченна дискретно-імпедансна товуються для розрахунку й подальшої побудови площина S на якій знаходяться імпеданс-ні смуги, діаграм направленості, а також визначення велищо примикаються одна до одної (фіг.2), розміри чини коефіцієнта направленої дії D шляхом чисеяких відповідають зонам Френеля, які визначені в льного інтегрування. результаті виконаної згідно формули (1) процедуНаведемо деякі результати розрахунку, що піри дискретизації. Опромінювач у вигляді системи l дтверджують переваги дискретно-імпедансного ниткоподібних струмів розміщений у фокусі дисрефлектора порівняно з дискретно-плоским рефкретної поверхні. лектором типу лінзи Френеля. Чисельний аналіз Треба знайти розподіл розсіяного поля в дапроводився для чотирьох варіантів дискретного лекій зоні, розрахувати діаграму спрямованості й рефлектора: коефіцієнт направленої дії (КНД) дискретно- модель 1 (прототип): дискретно-плоский реімпедансного рефлектора, задаючи різні значення флектор з параметрами Re  1 0 , Im  1 0 , комплексного поверхневого імпедансу на непаRe  2n 1 , Im  2n 0 , що відповідає класичній лінрних і парних зонах Френеля. зі Френеля з ідеальним провідником у непарних Потім, порівнюючи отримані результати з аназонах і повітряному заповненні в парних зонах. логічними розрахунками, виконаними для моделі - модель 2: дискретно-імпедансний рефлектор класичної лінзи Френеля, оцінити виграш у КНД 5 15446 з параметрами Re  1 0 , Re  2n 1 , Im  2n 0 , що відповідає дискретному рефлектору з ідеальним провідником у непарних зонах і з магнетиком у парних зонах. - модель 3: дискретно-імпедансний рефлектор з параметрами Re  1 0 , Im  1 0, Re  2n 0 , Im  2n 0 , що відповідає дискретному рефлектору з ідеальним провідником у непарних хонах і з «ємнісним» характером реактивного імпедансу в парних зонах. - модель 4: дискретно-імпедансний рефлектор з параметрами Re  1 0 , Im  1 0 , Re  2n 0 , Im  2n 0 , що відповідає рефлектору з ідеальним провідником у непарних зонах і з «індуктивним» характером реактивного імпедансу в парних зонах. Тут ми ввели наступні позначення:  1 - значення імпедансу в непарних зонах Френеля,  2n  2 /  0 - значення нормованого імпедансу в парних зонах Френеля, 0 120 -імпеданс віль ного простору. Розмір рефлектора S 50 , фокусна відстань f=0,5 S , - довжина хвилі. Наведемо результати виконаних розрахунків. Розрахунки показали, що для прототипу (модель 1) коефіцієнт направленої дії Do=17,93 дБ, а рівень ближніх бічних пелюстків ДН становить приблизно - 8,0 дБ. Переваги дискретно-імпедансної моделі ілюструють фіг.З і фіг.4, де показані діаграми спрямованості, розраховані для моделі 2 з параметрами Re 2n 15, m 2n 0, , що відповідає дискретноімпедансному рефлектору з ідеально провідними непарними зонами і з магнетиком у парних зонах. У порівнянні із прототипом ширина головної пелюстки ДН стає меншою, а рівень перших бічних пелюсток знижується до -12 дБ. Для того, щоб з'ясувати який характер залежності КНД від величини нормованого імпедансу є в парних зонах, була пророблена серія відповідних розрахунків. Результати для моделі 2, що відображають залежність КНД від величини нормованого імпедансу наведені на фіг.5. Графік, зображений на фіг.6 показує залежність виграшу AD в КНД стосовно прототипу AD=D-Do, одержуваний для моделі 2. З наведених графіків видно, що КНД дискретноімпедансного рефлектора спочатку різко зростає, потім швидкість зростання сповільнюється, і величина одержуваного виграшу асимптотично прямує до значення AD 2,5 дБ. Схожі результати отримані під час розрахунку діаграм направленості для моделі 3 з параметрами Re  2n 0 , Im  2n 15 , що відповідають дискретно-імпедансному рефлектору з ідеально провідними непарними зонами й з «ємнісним» характером чисто реактивного імпедансу в парних зонах (фіг.7 та фіг.8). Залежність КНД від величини імпедансу й виграш у КНД, одержуваний у цьому випадку відображають графіки, показані на фіг.9 і фіг 10. 6 Мало відрізняються і результати, отримані при розрахунку діаграм направленості для моделі 4 з параметрами Re  2n 0 , Im  2n 15 , що відповідає дискретно-імпедансному рефлектору з ідеально провідними непарними зонами і з «індуктивним» характером чисто реактивного імпедансу в парних зонах (фіг.11 і фіг.12). Виграш у КНД при  n 15 складає близько 2,5 дБ, що де вище, ніж для моделей 2 і 3. Проте, залежності КНД і виграшу, наведені на фіг.13 та фіг.14. у цьому випадку при  n 10 мають не «монотонний», а сильно порізаний характер, що пояснюється виникненням у парних зонах струму поверхневих хвиль. Висновок: результати виконаних розрахунків на моделях дискретно-імпедансних рефлекторів і порівняння отриманих результатів з характеристиками канонічної моделі дискретно-плоского рефлектора (лінзи) Френеля показали наступне: - дискретно-імпедансні рефлектори забезпечують більш вузьку головну пелюстку ДН і більш низький рівень ближніх бічних пелюсток; - дискретно-імпедансні рефлектори, в яких має місце чергування зон Френеля з різ відмінним за величиною поверхневим імпедансом у сусідніх зонах, дозволяють отримати виграш у КНД, якій досягає 2,5 дБ. Література. 1. Кольер Р., Беркхарт К., Лин Л. Оптическая голография. -М: Мир, 1973, 354 с. 2. Базарский О.В., Колесников А.И., Хлянич Я.Л. Частотные свойства зонированных линз Френеля. // Радиотехника и электроника. № 12, 1980. З. Байбулатов Ф.Х., Минин И.В. Исследование фокусирующих свойств зонной пластинки Френеля.// Радиотехника и электроника. - № 9, 1985. 4. Цалиев Т.А. Электродинамические свойства дискретных поверхностей // Известия вузов. Радиоэлектроника. - 2000. - 43. № 5-Ю. - с.13-22. 5. Марков Г.Т., Чаплин А.Ф. Возбуждение электромагнитных волн. – М - Л: Энергия, 1967.-376 с. б. Жук М.С., Молочков Ю.Б. Проектирование антенно-фидерных устройств. М. - Л., Энергия, 1966,-648 с. Перелік фігур креслення Фіг.1. Дискретизація плоскої поверхні Фіг.2. Геометрія задачі Фіг.3. Діаграма спрямованості рефлектора (модель 2 з параметрами Re  1 0 , Im  1 0 , Re  2 15 , Im  2 0 ). Фіг.4. Діаграма спрямованості рефлектора (модель 2). Фіг.5. Коефіцієнт спрямованої дії (КСД) рефлектора (модель 2). Фіг.6. Виграш у КСД дискретно-импедансного рефлектора (модель 2). Фіг.7. Діаграма спрямованості рефлектора (модель 3 з параметрами Re  1 0 , Im  1 0 , 15 ). Re  2 0 , Im  2 Фіг.8. Діаграма спрямованості рефлектора (модель 3). Фіг.9. Коефіцієнт спрямованої дії (КНД) рефле 7 15446 8 ктора (модель 3). Фіг.12. Діаграма спрямованості рефлектора Фіг.10. Виграш у КСД дискретно-импедансного (модель 4). рефлектора (модель 3). Фіг.13. Коефіцієнт спрямованої дії (КСД) рефФіг.11. Діаграма спрямованості рефлектора лектора (модель 4). Фіг.14. Виграш у КСД дискретно-импедансного (модель 4 з параметрами Re  1 0 , Im  1 0 , рефлектора (модель 4). Re  2 0 , Im  2 15 ). 9 Комп’ютерна верстка Г. Паяльніков 15446 Підписне 10 Тираж 26 прим. Міністерство освіти і науки України Державний департамент інтелектуальної власності, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601