Процес синтезу гібридних алгоритмів багатоальтернативного розпізнавання образів на основі перевірки складних статистичних гіпотез за критерієм максимуму апостеріорної імовірності

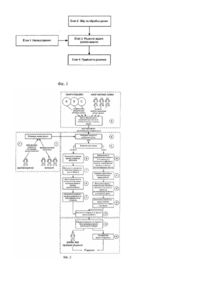
Корисна модель відноситься до галузі автоматики та штучного інтелекту і може бути використана в засобах обчислювальної техніки для автоматичного прийняття рішень, наприклад, в системах контролю доступу, робототехнічних системах та системах розпізнавання стану об'єктів керування. Відомий процес (див. [1]) синтезу багатоальтернативних статистичних оптимальних за критерієм максимуму апостеріорної імовірності (МАІ) алгоритмів розпізнавання образів (станів фізичних, хімічних, біологічних, соціальних та інши х процесів), який базується на визначенні еталонних описів образів, що розпізнаються, у вигляді щільності імовірності wi (s) виду (1): w i (s ) = Á é Rij ê pijr wirj s j, s'ijr , s ' 'ijr + ê ê r =1 ë ( Õå j =1 Dij ù d =1 ú û ) å pijdd(s j - sijd )ú ú (1) де Á - евклідового простору кількісних ознак S, які являють собою параметри, що вимірюються технічними засобами, станів процесів, яки розпізнаються. Кожен співмножник містить Rij щільностей імовірностей ( w ijr s j, s'ijr , s' 'ijr ) [ еталонного розподілу ознаки s j на кожному r-ому еталонному інтервалі s'ijr , s' 'ijr ( ) ] можливих значень ознаки s j і Dij функцій Дирака d s j - sijd , що відповідають крапковим еталонним значенням s j для кожного з образів, які розпізнаються. При цьому p ijr та p ijd являють собою апріорні умовні імовірності { } { } спостереження r-го інтервалу, r Î 1,2, K , R ij , або d-ro значення, d Î 1,2, K , D ij , при спостереженні образу Ui у метриці ознаки s j . Для імовірностей p ijr , p ijd потрібне дотримання умов нормування (2): Rij pij = å Dij pijr + r =1 åp ijd = 1, "i Î { ,2, K, L}, "j Î {1,2,K , Á} 1 (2) d=1 де L - кількість образів, які розпізнаються. Відомий процес дозволяє вибрати дискретно-аналогове нерандомизоване МАІ- оптимальне правило d , що 1 , розділяє вибірковий простір X оцінок параметрів на L непересічних областей Xi, i Î { ,2, K, L } L U X = X для образів, i i=1 які задані у метриках кількісних ознак інтервалами та дискретними значеннями обмірюваних параметрів процесів. Недоліком цього процесу є неможливість вирішення задачі автоматичного розпізнавання образів, які задані сумісно в просторах кількісних ознак (параметрів процесів, що вимірюються технічними засобами) та якісних ознак (параметрів процесів, що оцінюються експертами на основі власного досвіду).Це робить цей процес нездатним вирішувати задачі розпізнавання об’єктів, які задані нечіткими параметрами. Ці параметри використовуються людьми у повсякденному житті та можуть приймати значення фраз природної або штучної мови. Наприклад, параметр, який характеризує швидкість, може мати наступні значення „висока”, „середня”, „дуже низька” та т.п. В основу корисної моделі поставлена задача створення процесу синтезу алгоритмів розпізнавання образів, який дозволив би оптимізувати за критерієм МАІ процедури прийняття рішень при розпізнаванні образів, які задані еталонними описами у вигляді сумісно як значень та інтервалів значень кількісних (вимірюваних) ознак, так і термів якісних (логічних) ознак, шляхом введення нових операцій для збору, обробки та застосування якісних ознак. Поставлена задача вирішується тим, що еталонні описи образів в термах нечітких лінгвістичних змінних та судження експертів при виборі рішень формалізуються таким чином, щоб забезпечити їх визначення в евклідових просторах та урахування при автоматичному прийнятті рішень сумісно з кількісними ознаками і вибірками їх оцінок (результатів вимірювань ознак технічними засобами). Суть корисної моделі пояснюється кресленнями, на яких подано: Фіг.1 - загальна схема процесу синтезу гібридних алгоритмів багато альтернативного розпізнавання образів на основі перевірки складних статистичних гіпотез за критерієм максимуму апостеріорної імовірності; Фіг.2 - детальна схема процесу. Сутність запропонованого способу полягає в наступному. Для використання параметрів процесів, що оцінюються експертами на основі власного досвіду вводяться метрики якісних ознак. Кожна з цих ознак являє собою деяку j-ю, j Î { ,2,K , Á} , лінгвістичну (висловлювальну) 1 ~ змінну з заданими на ній термами. Кожному образу зіставляються один або декілька Tij термів Uijt , t Î 12, K, Tij . , ( ) { } Кожному терму ставиться у відповідність єдине індивідуальне ціле. При цьому кожному образу Ui у множині s j , еквівалентних значень j-й нечіткої висловлювальної змінної буде відповідати деяка множина Zij Ì sj цілих sijt Î Z ij . Кожне з цілих формалізує можливе судження експерта відносно образу Ui . Упорядковуються введені цілі в множині s j рівномірно з одиничним кроком і наділяються s j властивостями евклідового простору. Задаються на множині s j координати кожної крапки sijt . Це робиться за допомогою функції ( ) Дирака d s j - sijt . Отримана в такий спосіб множина s j являє собою результат відображення лінгвістичної змінної в метричний (евклідів) простір ознак. Визначаються апріорні функції приналежності mUij : S ® [0,1] нечіткої множини { ( ) } ( ( ) ~ Uij = mUij s j / s j , s j Î S, mUij s j Î [0,1] , що відповідає образові Ui ; у метриці ознаки s j , у вигляді ) Tij ( ) å pijtd(s j - sijt ) mUij sj = (3) t =1 де p ijt Î [0,1] - експертна оцінка ступеню приналежності t-го терму і-му образові в просторі нечітких ~ висловлень j-й лінгвістичної змінної. Нечіткі множини Uij являють собою еталонні описи образів Ui , які розпізнаються, у лінгвістични х змінних, відображених на евклідів простір S ознак s j . Tij åp Якщо вимагати дотримання умов нормування ijt = 1 , то p ijt можна інтерпретувати як апріорну імовірність t =1 ( того, що t-й терм j-ої висловлювальної змінної належить і-му образові. При цьому функцію d s j - sijt ) можна трактувати як аналог диференціальної функції розподілу цілого sijt . Введемо модель складного еталонного опису wi (s) образів, що розпізнаються, на основі гібридизації функції приналежності (3) і моделі складного еталонного опису вигляду (1), вважаючи ознаки незалежними: Dij Tij ü Á ì é R ij ù ï ê ú + (1- n ) p d s - s ï wi (s ) = pijrw ijr s j , s'ijr , s' 'ijr + pijdd s j - s ijd (4) ín j ê i ijt j ijt ý ú ï j=1 ï ë r =1 d =1 t =1 ê ú û î þ ( Õ å Rij å Dij pijr + r =1 ( å ) å Tij pijd = 1 , d =1 åp ijt ( ) å ( ) = 1 "i Î { ,2, K , L} "j Î { ,2, K, Á}, , 1 , 1 t =1 де w ijr s j, s'ijr , s' 'ijr ) - апріорні щільності розподілу кількісної ознаки s j , які визначаються при навчанні [ ] { } ( ) алгоритму на кожнім з Rij еталонних інтервалів s'ijr , s' 'ijr , r Î 1,2, K , R ij ; d s j - sijd - функції Дирака, як щільності імовірності математичних очікувань sijd кожного з Dij можливих дискретних еталонних значень ознаки s j , що { } допускає кількісне оцінювання, d Î 1,2, K , D ij ; p ijr та p ijd - апріорні умовні імовірності спостереження r-го інтервалу або d-ro значення при спостереженні образу Ui у метриці ознаки s j ; n j - індикатор виду ознаки, n j = 1 , якщо s j оцінюється кількісно і n j = 0 , якщо якісно. Еталонний опис (4) образу Ui у силу введених нормувань і допущень може розглядатися як аналог Á-мірної ( спільної щільності імовірності W s Ui ) = wi (s) змішаного типу вектора s незалежних ознак на множині Ui , визначену в області s j евклідового Á-мірного простору ознак S. Надалі (4) будемо називати «гібридним» складним еталонним описом образів, які розпізнаються. При цієї моделі простору ознак вибірковий простір також являє собою евклідів простір (z ´ Á - мірний), на якому може бути введена наступна функція правдоподібності W(x|s) гібридного типу, що є функцією вектором s: æ Á ç (5) Wç x s ) = n jW j x j s j - n j + 1 1 - n j msj x j + n j ç j =1 è Õ [ ( ) ][( ) ( ) ] W (x s ) - частинна умовна функція де j j j оцінювання, при змінної s j ; ms j значень ( ) ( ms j x j ³ 1 ; оцінок j-й правдоподібності вибірки j-ї ознаки, що припускає кількісне x j Î [0,1] - функція приналежності змінної нечіткої множини ~j еквівалентних s ( ) висловлювальної змінної, що володіє властивостями щільності імовірності ¥ ò m (x )dx= sj j j 1 ), і яка задовольняє умові -¥ ò m (x )d(s - s )ds = m (x ) sj s ij j j ijt j Uij j (6) ( ) де Sij - область визначення і-го образу в метриці j-ої ознаки; ms j x j - умовна функція приналежності вибіркових значень j-ої ознаки при спостереженні і-го образу. Введені моделі (4) та (5) об'єктивно відображають той факт, що в ході експертного оцінювання якісних характеристик образів, які розпізнаються, помилки кваліфікованих експертів у нечітких умовах іспитів носять випадковий характер. Це обумовлює правомірність накладення таких же обмежень на функції приналежності, як і на щільності імовірності, і дозволяє при синтезі алгоритмів прийняття рішень розглядати кількісні і якісні ознаки з єдиних позицій і в одній системі координат, а також формулювати і вирішувати задачу синтезу автоматів, що розпізнають, за аналогією з методами статистичного виводу розв'язуючих правил. Узагальнимо наведений в [2] вираз для апостеріорної імовірності справедливості і-ої складної гіпотези на фоні складної альтернативи на випадок багатоальтернативного розпізнавання образів, які задані складними гібридними еталонними описами (4): ò ( ) pi W x s wi (s)ds { } P s Î Si x = Si = L å p ò W(x s )w q q =1 q (s )ds Sq Á ì é R ij Dij ù Tij ü j=1 ï ê r =1 î ë d =1 ú û t =1 ï þ ( )Õ ïn j êå pijr wijr (s j, s'ijr , s' 'ijr ) + å pijdd(s j - sijd )ú + (1 - n j )å pijt d(s j - sijt )ïds ´ í ê ý ú ò pi W x s Si Á L ì é Rij ï ê pqjr w qjr s j , s' qjr , s' 'qjr + ín j ê ï ê r=1 î ë ( å p ò W (x s )Õ å ´ q q= 1 j =1 Sq ù ú + 1- n j ú ú û D ij ) å pqjd d(s j - s qjd ) ( d =1 ü ï ýds ï þ T ij -1 )å pqjt d(s j - s qjt ) t= 1 i = 1,2, K, L, L ( ) де pi p q - апріорні імовірності спостереження і-го (q-ro) образів, å p = 1. i i =1 Відповідно до критерію максимуму апостеріорної імовірності порівнюються апостеріорні імовірності { } p s Î Si x . Для цього визначається їхнє відношення, що у розглянутому випадку має вигляд: Á ì é R ij Dij ù Tij ü j=1 ï ê r =1 î ë d=1 ú û t =1 ï þ ( )Õ ïn j êå pijr w ijr (s j , s'ijr , s' 'ijr ) + å pijdd (s j - sijd )ú + (1- n j )å pijtd (s j - sijt )ïds ´ í ê ý ú ò pi W x s Si Á ì é Rij ï ê p1jr w1jr s j , s'1jr , s' '1jr + ín j ê ï ê r=1 ë î ( ò ( )Õ å ´ p1 W x s j =1 S1 ù ú + 1- n j ú ú û Dij ) å p1jd d(s j - s1jd ) ( d= 1 pi wi (x ) pi = L (x ), i = 2,3, K, L, p1w1(x ) p1 i ü ï ýds ï þ Tij )å p1jt d(s j - s1jt ) t =1 -1 = де Li (x) - відношення усереднених функцій правдоподібності wi (x ) . Приймається рішення gi, i = 2,3, K , L , якщо gi dмав : pi L i (x) = max pq L q (x ), (7) 2 £q £L (pq p1 )L q (x) ³ 1, q = 2,3,K , L, і рішення g1 , якщо (p q p 1 )L q (x )á1 "q = 2,3, K, L. , У силу того, що фільтруюча властивість d - функції ò m (x )d (s - s )ds = m (x ) sj j j ijt j Uij (8) j S ij ( ) довизначає функцію ms j x j приналежності змінної нечіткої множини ~j еквівалентних значень оцінок j-й s висловлювальної змінної на координати конкретної крапки sijt , що відповідає терму Uijt , то з (3) та (6) випливає: Tij ( ) å pijtmU (x j ) . mUij x j = ijt t =1 При цьому усереднені функції wi (x ) правдоподібності можуть бути зведені до вигляду: wi (x ) = ò W(x s)w ds = i si (9) ì é Rij ü Dij ù Tij ï ê ï ú = pijr W j x j s j wijr s j, s'ijr , s' ' ijr ds j + pijd W j x j sijd ú + 1- n j pijt mUijt x j ý ín j ê ï ú j =1 ï ê r =1 d=1 t =1 s ij û î ë þ Процес синтезу гібридних алгоритмів багатоальтернативного розпізнавання образів на основі перевірки складних статистичних гіпотез за критерієм максимуму апостеріорної імовірності реалізується таким чином. На етапі попереднього налаштування адміністратор проводить виявлення вагомих ознак процесу, що розпізнається (крок 1) та здійснюється опитування експертів з метою отримання відповідей на питання в метриках якісних ознак (крок 2). На етапі збору та обробки (крок 3) даних отримуються значення ознак з різноманітних те хнічних засобів (датчиків, вимірювачів, медичного обладнання, пристроїв відео спостереження та інших). Значення нечітких параметрів (якісних ознак) отримуються у ході спілкування з носіями нечіткою логіки (людьми), які для оцінювання значень якісних ознак використовують лінгвістичні змінні, що приймають значення фраз природної або штучної мови. Á Õ å ò ( ) ( ) å ( ) ( )å ( ) На етапі вирішення задачі розпізнавання вводиться модель складного еталонного опису образів, що розпізнаються (крок 4). Для рішення цієї задачі необхідно в залежності від типу ознаки виконати ряд кроків, які розглянуті нижче. Визначення кроків для конкретної ознаки здійснюється за допомогою селектора типа ознаки (крок 5). Для кількісних ознак визначаються в явному вигляді еталонні розподіли, наприклад, як одномірні щільності імовірності випадкових величин, розподілених за рівномірним законом у межах. ( ) Для кількісних ознак (крок 6) визначаються в явному вигляді еталонні розподіли w ijr s j, s'ijr , s' 'ijr , наприклад, [ ] як одномірні щільності імовірності випадкових величин, розподілених за рівномірним законом у межах s'ijr , s' 'ijr . ( ) Надалі (крок 7) визначаються дискретні еталонні значення sijd та функції Дирака d s j - sijd , як щільності імовірності постійних величин sijd . Для якісних ознак (крок 10) визначаються та упорядковуються рівномірно з одиничним кроком цілі значення sijt , які ставляться у відповідність образам Ui у множині s j , еквівалентних значень j-й нечіткої висловлювальної ( ) змінної. За допомогою функції Дирака d s j - sijt задаються координати кожної крапки sijt на множині s j . Для кількісних ознак (крок 8) вводяться та визначаються в явному вигляді моделі частинних умовних функцій ( ) правдоподібності Wj x j s j , наприклад, як z - мірні умовні сумісні щільності імовірності нормального розподілу z незалежних вимірів кожної j-ої кількісної ознаки при умові, що математичне очікування прийняло значення s j . ( ) Для якісних ознак (крок 11) задаються аналітичні моделі функцій приналежності ms j x j , наприклад, у вигляді z - мірних гаусоїд або інших функцій, які відображають характер розподілу можливих помилок експертів при ( ) судженні відносно кожної j-ої якісної ознаки та відповідають умовам: ms j x j ³ 1 ; ( ) ¥ ò m (x )dx = 1. sj j j -¥ Вирішуючи рівняння (8), визначаються функції mUijt x j приналежності множини еквівалентних значень оцінок j-й висловлювальної змінної у конкретної крапці sijt , що відповідає терму Uijt образу Ui . { } Визначаються апріорні умовні імовірності p ijr та p ijd спостереження r-го інтервалу, r Î 1,2, K , R ij , та d-ro { } значення, d Î 1,2, K , D ij , при спостереженні образу Ui у метриці кожної кількісної ознаки s j (крок 9). Визначаються p ijt - експертні оцінки ступеню приналежності t-ro терму і-му образу в просторі нечітких висловлень кожної лінгвістичної змінної (якісної ознаки). Визначаються р ijt-експертні оцінки ступеню приналежності t-ro терму і-му образу в просторі нечітких висловлень кожної лінгвістичної змінної (крок 13). Для кожного з образів, що розпізнаються, визначаються усереднені функції правдоподібності вигляду (9) та апріорні імовірності рi, спостереження кожного і-го образу (крок 14). На останньому етапі прийняття рішення будується вирішальне правило багатоальтернативного розпізнавання образів за критерієм МАІ (крок 15). Остаточне рішення може бути отримано в автоматичному режимі або особою, яка обирає рішення з запропонованих варіантів (крок 16). Таким чином, корисна модель, що заявляється, дозволяє синтезувати алгоритми багатоальтернативного розпізнавання образів, які задані як кількісними, так і якісними ознаками, на основі перевірки складних статистичних гіпотез за критерієм максимуму апостеріорної імовірності. В свою чергу ці нові властивості дозволять розширити межі використання цієї корисної моделі за рахунок галузей, в яких домінує використання нечітких параметрів опису образів. Наприклад, отримання медичного діагнозу стану організму хворого, прогнозування політичних явищ, розвитку військових конфліктів, контроль демографічного стану країни або місцевості та багато ін.), що є неможливим при використанні прототипу. Джерела інформації: 1. Певцов Г.В., Лупандин В.А. Синтез алгоритмов многоальтернативного распознавания образов на основе проверки сложных статистических гипотез по критерию максимума апостериорной вероятности // Известия вузов. Радиоэлектроника. - 2001. - Т.44, №11. - С.77-80; 2. Левин Б.Р. Теоретические основы статистической радиотехники. Книга 2. - М.: Сов. радио, 1975. - 392с.