Спосіб визначення головного моменту дисбалансів роторів
Номер патенту: 41467
Опубліковано: 25.05.2009
Автори: Дзюндзюк Борис Васильович, Мамонтов Олександр Вікторович
Формула / Реферат
Спосіб визначення головного моменту дисбалансів роторів, що включає установку їх на маятникову раму, вимірювання частот вільних коливань її в чотирьох положеннях, одержуваних при повороті ротора навкруги своєї осі кожного разу на дев'яносто градусів, і математичний розрахунок, який відрізняється тим, що перед математичним розрахунком визначають головний вектор дисбалансів, його кут і відстань між точкою, рівновіддаленою від площин корекції, і точкою перетину осі виробу з віссю коливань маятникової рами, а головний момент дисбалансів і його кут обчислюють за формулами:
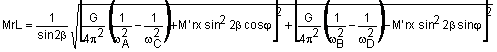 ,
,
де MrL - головний момент дисбалансів ротора,
β - кут між осями (N-N) і (S-S),
G - коефіцієнт жорсткості пружного елемента маятникової рами,
М'r - величина головного вектора дисбалансів,
φ - кут головного вектора дисбалансів,
х - відстань між точками О і О* ,
ωА, ωB, ωC, ωD - частоти вільних коливань рами при відповідних положеннях ротора (1),
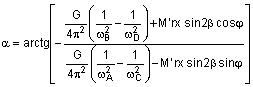 ,
,
де α - кут головного моменту дисбалансів ротора.
Текст
Спосіб визначення головного моменту дисбалансів роторів, що включає установку їх на маятникову раму, вимірювання частот вільних коливань її в чотирьох положеннях, одержуваних при повороті ротора навкруги своєї осі кожного разу на дев'яносто градусів, і математичний розрахунок, який відрізняється тим, що перед математичним розрахунком визначають головний вектор дисбалансів, його кут і відстань між точкою, рівновіддаленою від площин корекції, і точкою перетину осі виробу з віссю коливань маятникової рами, а головний момент дисбалансів і його кут обчислюють за формулами: , де MrL - головний момент дисбалансів ротора, β - кут між осями (N-N) і (S-S), G - коефіцієнт жорсткості пружного елемента маятникової рами, М'r - величина головного вектора дисбалансів, φ - кут головного вектора дисбалансів, х - відстань між точками О і О* , ωА, ωB, ωC, ωD - частоти вільних коливань рами при відповідних положеннях ротора (1), ⎡ G ⎛ 1 ⎤ 1 ⎞ ⎜ ⎢ − 2 ⎟ + M' rx sin 2β cos ϕ ⎥ 2 ⎜ 2 ⎟ ⎢ 4π ⎝ ωB ωD ⎠ ⎥ α = arctg⎢− ⎥, ⎛ 1 ⎞ G ⎜ 1 ⎢ ⎥ − 2 ⎟ − M' rx sin 2β sin ϕ ⎥ ⎢ 4π2 ⎜ ω2 ωC ⎟ ⎢ ⎥ ⎝ A ⎠ ⎣ ⎦ де α - кут головного моменту дисбалансів ротора. Корисна модель належить до засобів визначення дисбалансу тіл обертання. Відомий спосіб визначення моменту інерції тіл, полягаючий в тому, що виріб закріплюють на маятниковій рамі, забезпечують збіг центру маси і центру підвісу у вертикальній площині, порушують вільні коливання рами шляхом поштовху і виміряють період коливань, по якому після математичних розрахунків визначають момент інерції (А. С. СССР №533845, G01 M1/10). Даний спосіб близький по технічному єству до запропонованого способу, проте має обмежені технічні можливості. Він не дозволяє визначати кут і величину головного моменту дисбалансів ротора. Найближчим до запропонованого рішення є спосіб визначення статичного дисбалансу виробів, що включає маятникову раму, підпружинену за допомогою пружного елемента, і барабан зі встановленим в нього виробом, які здійснюють вільні коливання навкруги вертикальної осі. Барабан має можливість обертання навкруги своєї осі. Кут і величину дисбалансу виробу розраховують за частотами вільних коливань рами, зміряних при чоти рьох положеннях барабана. Кожне положення барабана отримують при його повороті відносно своєї осі на 90° (А. С. СССР №1825996, Кл. G 01 М 1/10, опубл. 07.07.93, Бюл. №25). Недоліком цього способу в порівнянні із запропонованим є також неможливість визначення кута і величини головного моменту дисбалансів ротора. Задачею запропонованого способу є визначення кута і величини головного моменту дисбалансів ротора для його балансування. Це досягається за рахунок того, що момент дисбалансу і його кут обчислюють по формулам за допомогою зміряних частот вільних коливань маятникової рами при чотирьох положеннях ротора, які отримують при його повороті навкруги своєї осі кожного разу на 90°. Поставлена задача вирішується таким чином. У способі визначення головного моменту дисбалансів роторів, який включає їх установку на маятникову раму, вимірювання частот вільних коливань її в чотирьох положеннях, одержуваних при повороті ротора навкруги своєї осі кожного разу на 1 sin 2β 2 2 G 1 1 G 1 1 − + M' rx sin2 2β cos ϕ + − − M' rx sin2 2β sin ϕ 2 2 2 4π2 ω2 ωC 4π2 ωB ωD A (19) UA (11) 41467 (13) U MrL = 3 41467 дев'яносто градусів, і математичний розрахунок, згідно корисної моделі, перед математичним розрахунком визначають головний вектор дисбалансів, його кут і відстань між точкою, рівновіддаленою від площин корекції, і точкою перетину осі виробу з віссю коливань маятникової рами, а потім головний момент дисбалансів і його кут обчислюють за формулами: MrL = 1 sin 2β ⎡ G ⎛ 1 ⎢ 2⎜ 2 ⎢ 4π ⎜ ωA ⎝ ⎣ − 2 2 ⎤ ⎡ ⎤ ⎛ ⎞ 1 ⎞ ⎟ + M' rx sin2 2β cos ϕ⎥ + ⎢ G ⎜ 1 − 1 ⎟ − M' rx sin2 2β sin ϕ⎥ 2 2 2 ω2 ⎟ ⎥ ⎢ 4π ⎜ ωB ωD ⎟ ⎥ ⎝ ⎠ C⎠ ⎦ ⎦ ⎣ ; де MrL - головний момент дисбалансів ротора; β - кут між осями (N-N) і (S-S); G - коефіцієнт жорсткості пружного елементу маятникової рами; М'r- величина головного вектора дисбалансів; φ - кут головного вектора дисбалансів; х - відстань між точками О і О* ; ωА, ωB, ωC, ωD - частоти вільних коливань рами при відповідних положеннях ротора 1; ⎤ ⎡ ⎞ ⎛ G ⎜ 1 1 ⎟ ⎥ ⎢ ⎜ 2 − 2 ⎟ + M' rx sin 2β cos ϕ ⎥ ⎢ 4π2 ⎜ ω ω ⎟ ⎥ ⎢ D⎠ ⎝ B α = arctg⎢− ⎥ ⎛ ⎞ ⎥ ⎢ G ⎜ 1 1 ⎟ ⎢ − − M' rx sin 2β sin ϕ ⎥ 2 ⎜ ω2 ω2 ⎟ ⎥ ⎢ 4π ⎜ ⎟ ⎥; ⎢ C⎠ ⎝ A ⎦ ⎣ α - кут головного моменту дисбалансов ротора. На Фіг.1 показана схема пристрою для реалізації способу визначення головного моменту дисбалансів ротора із статичною і динамічною неврівноваженістю. На Фіг.2 показана схема із динамічною неврівноваженістю. Пристрій включає ротор 1, встановлений на маятникову раму (на Фіг. не показана). Вісь ротора 1 (N-N) повернена на 45° відносно осі вільних коливань (S-S), які перехрещуються в точці О*. Точка О рівновіддалена від площин корекції ротора 1, в яких розташовані умовні неврівноважені маси 2 … 5. Маси 2, 3 являють собою статичну неврівноваженість, маси 4, 5 являють собою динамічну неврівноваженість виробу 1. Пристрій також включає елементи фіксації ротора 1 в чотирьох положеннях, які отримують при його обертанні навкруги своєї осі кожен раз на 90°, а також елементи вимірювання частоти коливань рами (на Фіг. не показані). Спосіб здійснюється таким чином. Досліджуваний ротор 1 встановлюють на маятникову раму і фіксують в неї. Рамі додають поштовх і виміряють частоту затухаючих вільних коливань. Після цього 4 ротор повертають навколо своє й осі на 90° і знову виміряють частоту. Цю операцію повторюють ще двічі, повертаючи ротор кожного разу на 90°. Далі одним з відомих способів визначають кут і величину головного вектора дисбалансів (наприклад, А. С. СССР №1825996, Кл. G 01 М 1/10, опубл. 07.07.93, Бюл. №25). Потім вимірюють величину х - відстань між крапкою О (рівновіддаленою від площин корекції) і крапкою О* (перетином осі ротора 1 і осі рами). Величина х викликана технологічним розкидом довжини L виробу 1. Після цього виконують математичний розрахунок. Розглянемо більш докладніше суть корисної моделі. Головний момент дисбалансів може бути замінений моментом пари рівних антипаралельних дисбалансів, розташованих в двох площинах корекції. Головний вектор дисбалансів також може бути замінений вектором пари рівних за значенням паралельних дисбалансів, розташованих в двох площинах корекції (М.Е. Левит, «Балансировка деталей и узлов». Машиностроение, 1986г. стр.29). Значить, моментную неврівноваженість можна звести до наявності двох однакових мас 4 і 5, а статичну неврівноваженість можна звести до наявності двох однакових мас 2 і 3, розташованих у відповідних площинах корекції. Значення моменту інерції системи відносно осі (S-S) дорівнює (А. А Яблонский, «Курс теоретической механики», часть 2, динамика, изд. 5. М., «Высшая школа», 1977г., стр. 92, формула 34.2): J = mc 2 + mc 2 + m' f 2 + m' f 2 + J0 , 1 1 b=(l+x)sin β+k cos β=(l+x)sin β+r cos(180°(4) -α)cos β=(l+x)sin β-r cos α cos β. Підставляючи вирази (3) і (4) в (2), отримаємо: 2 2 2 2 2 2 2 2 2 2 2 2 с =r sin α+(l+х) sin β-2(l+x)sinβ·r·cosαcosβ+r cos αcos β=r sin α+(l+x) sin β2 2 2 r(l+x)cosαsin2β+r cos αcos β. α); Аналогічно: 2 2 2 (6) с1 =α1 +b1 , 2 2 2 2 2 2 2 2 r =α1 +k1 =α1 +[r cos(180°-α)] =α1 +r cos (180°2 2 2 2 r -r cos (180°-α)=α1 ; 2 2 0 2 r sin (180 -α =α1 ; α1=r sin(180°-α)=r sin α; (7) (1) де m - значення маси 4 (5); m’ - значення маси 2 (3); с і с1 - відстань між відповідною масою 4 (5) і віссю (S-S); f і f1 - відстань між відповідною масою 2 (3) і віссю (S-S); Jo - момент інерції системи відносно осі (S-S) без мас 2, 3, 4, 5. З теореми Піфагора виходить (див. Фіг.2): 2 2 2 (2) с =а +b , k=r cos(180°-α); r2=а2+k2=а2+[rcos(180°-α)]2=a2+r2cos2(180°-α); r2-r2cos2(180°-α)=а2; 2 2 2 r sin (180°-α)=a ; α=r sin(180°-α)=rsin α; (3) (5) b1=(l-x)sin β+k1cos β=(l-x)sin β+r cos(180°(8) -α)cos β=(l-x)sin β-r cos α cos β. Підставляючи вирази (7) і (8) в (6), отримаємо: 5 41467 6 с12=r2sin2α+(l-x)2sin2β-2(l-x)sinβ·r·cosαcosβ+r2cos2αcos2β=r2sin2α+(l-x)2sin2β-r(l-x)cosαsin2β r2cos2αcos2β. Також з теореми Піфагора виходить (див. Фіг.1): f2=d2+e2; (10) n=r cos(φ-180°); e=r sin(φ-180°)=-r sin φ; (11) (9) d=n cos β+(l+x)sin β=-r cos φ cos β+(l+x)sin β (12) Підставляючи вирази (11) і (12) в (10), отримаємо: f2=r2cos2φcos2β-2rcosφcosφ(l+x)sinβ+(l2+2x+x2)sin2β+r2sin2φ=r2cos2φcos2β2 2 2 2 2 -r(l+x)sin2βcosφ+(l +2x+x )sin β+r sin φ. Аналогічно f12=d12+e12; n1=r cos(φ-180°)=-r cos φ; (13) e1=r sin(φ-180°)=-r sin φ; d1=(l-x)sin β-n1cos β=(l-x)sin β+r cos φ cos β; (14) 2 2 2 2 2 2 2 2 2 2 2 2 f1 =r sin φ+(l-x) sin β+2r(l-x)sinβcosβcosφ+r cos φcos β=r sin φ+(l-x) sin β+r(l-x)sin2βcosφ+r2cos2φcos2β. (15) Підставляючи вирази (5), (9), (13) і (15) в (1), отримаємо: 2 2 2 2 2 2 2 2 2 2 2 2 2 J=2m[r sin α+(l +x )sin β-rlcosαsin2β+ cos αcos β]+2m'[r sin φ+(l +x )sin β2 2 2 -rxcosφsin2β+r cos φcos β]+J0. Якщо експериментально зміряти значення JA, JB, JC, JD в чотирьох положеннях ротора 1 при відповідних кутах α (αB=αА+90°; αC=αA+180°; [ αD=αA+270°) і підставити в (16), то отримаємо систему рівнянь (17): ] ⎧JA = 2m r 2 sin2 α + (l2 + x 2 ) sin2 β − rl cos α sin 2β + r 2 cos2 α cos2 β + ⎪ ⎪+ 2m' r 2 sin2 ϕ + (l2 + x 2 ) sin2 β − rx cos ϕ sin 2β + r 2 cos2 ϕ cos2 β + J0 ⎪ ⎪ ⎪ 2 2 2 2 2 2 2 2 ⎪JB = 2m r cos α + (l + x ) sin β + rl sin α sin 2β + r sin α cos β + ⎪ 2 2 2 2 2 2 2 2 ⎪+ 2m' r cos ϕ + (l + x ) sin β + rx sin ϕ sin 2β + r sin ϕ cos β + J0 ⎪ ⎨ ⎪ 2 2 2 2 2 2 2 2 ⎪JC = 2m r sin α + (l + x ) sin β + rl cos α sin 2β + r cos α cos β + ⎪ 2 2 2 2 2 2 2 2 ⎪+ 2m' r sin ϕ + (l + x ) sin β + rx cos ϕ sin 2β + r cos ϕ cos β + J0 ⎪ ⎪ ⎪JD = 2m r 2 cos2 α + (l2 + x 2 ) sin2 β − rl sin α sin 2β + r 2 sin2 α cos2 β + ⎪ ⎪+ 2m' r 2 cos2 ϕ + (l2 + x 2 ) sin2 β − rx sin ϕ sin 2β + r 2 sin2 ϕ cos2 β + J0 ⎩ [ [ [ [ [ [ [ ] ] ] ] ] (17) ] ] Вирішуємо систему рівнянь (17): ⎧JA − JB = −4mrl sin 2β cos α − 4m' rx sin 2β cos ϕ = −MrL sin 2β cos α − M' rx sin 2β cos ϕ ⎪ ⎨ ⎪J − J = −4mrl sin 2β sin α + 4m' rx sin 2β sin ϕ = MrL sin 2β sin α + M' rx sin 2β sin ϕ ⎩ B D де L=2l; М=2m; М'=2m'; ⎧JA − JC + M' rx sin 2β cos φ = −MrL sin 2β cos α (19) ⎨ ⎩JB − JD − M' rx sin 2β sin ϕ = MrL sin 2β sin α (J A − JC + M' rx sin 2β cos φ)2 + (JB − JD − M' rx sin 2β sin φ)2 = M2r 2L2 sin2 2β. Виразивши значення моментів інерції через відповідні частоти вільних коливань (А. А Яблонский, «Курс теоретической механики», часть 2, ди (16) (18) Зведемо в квадрат рівняння (19): ⎧(JA − JC + M' rx sin 2β cos φ)2 = M2r 2L2 sin2 2β cos2 α ⎪ (20) ⎨ ⎪(JB − JD − M' rx sin 2β sin φ)2 = M2r 2L2 sin2 2β sin2 α ⎩ Додамо одне рівняння системи (20) до другого: (21) намика, изд. 5. М., «Высшая школа», 1977г., стр.220), отримаємо формулу для головного моменту дисбалансів ротора: 7 MrL = 1 sin 2β ⎡ G ⎛ 1 ⎢ 2⎜ 2 ⎢ 4π ⎜ ωA ⎝ ⎣ − 41467 8 2 2 ⎤ ⎡ ⎤ ⎛ ⎞ 1 ⎞ ⎟ + M' rx sin2 2β cos ϕ⎥ + ⎢ G ⎜ 1 − 1 ⎟ − M' rx sin2 2β sin ϕ⎥ . 2 2 2 ω2 ⎟ ⎥ ⎢ 4π ⎜ ωB ωD ⎟ ⎥ ⎝ ⎠ C⎠ ⎦ ⎦ ⎣ Розділимо друге рівняння системи (19) на перше: (22) JB − JD − M' rx sin 2β sin φ JA − JC + M' rx sin 2β cos φ Звідси отримаємо формулу для кута головного моменту дисбалансів: ⎡ ⎤ ⎛ ⎞ ⎢ ⎥ G ⎜ 1 1 ⎟ − ⎜ ⎟ + M' rx sin 2β cos ϕ ⎥ ⎢ 4π 2 ⎜ ω 2 ω 2 ⎟ ⎢ ⎥ D⎠ ⎝ B ⎥. α = arctg⎢− ⎛ ⎞ ⎢ ⎥ G ⎜ 1 1 ⎟ ⎢ ⎥ − ⎜ ⎟ − M' rx sin 2β sin ϕ ⎥ ⎢ ω2 ⎟ 4π 2 ⎜ ω 2 ⎢ ⎥ C⎠ ⎝ A ⎣ ⎦ tgα = − (23) Таким чином, запропонований Корисна модель дозволяє визначити кут і величину головного моменту дисбалансів ротора. 9 Комп’ютерна верстка Л. Купенко 41467 Підписне 10 Тираж 28 прим. Міністерство освіти і науки України Державний департамент інтелектуальної власності, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601
ДивитисяДодаткова інформація
Назва патенту англійськоюMethod for determination of main torque of rotor unbalance
Автори англійськоюMamontov Oleksandr Viktorovych, Dziundziuk Borys Vasyliovych
Назва патенту російськоюСпособ определения главного момента дисбалансов роторов
Автори російськоюМамонтов Александр Викторович, Дзюндзюк Борис Васильевич
МПК / Мітки
МПК: G01M 1/10
Мітки: спосіб, моменту, головного, роторів, визначення, дисбалансів
Код посилання
<a href="https://ua.patents.su/5-41467-sposib-viznachennya-golovnogo-momentu-disbalansiv-rotoriv.html" target="_blank" rel="follow" title="База патентів України">Спосіб визначення головного моменту дисбалансів роторів</a>
Попередній патент: Пристрій визначення тиску для контролю якості плодоовочевої продукції
Наступний патент: Змішувач
Випадковий патент: Спосіб зварювання труб з трубними ґратами









