Пристрій для перетворення на нуль сумарної провідності вузла у квазіаналогових моделях
Номер патенту: 104210
Опубліковано: 10.01.2014
Автори: Кривенко Віктор Іванович, Карандаков Генадій Васильович
Формула / Реферат
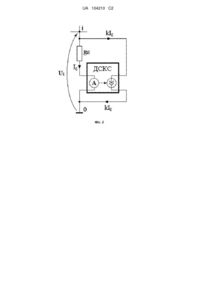
Пристрій для перетворення на нуль сумарної провідності вузла у квазіаналогових моделях, що містить гілку із резистором, провідність якого дорівнює сумі провідностей всіх інших гілок вузла, який відрізняється тим, що паралельно зазначеному резистору включено джерело струму, кероване струмом резистора із коефіцієнтом передачі ![]() , причому в контурі між точками і-0 напрямки струму резистора та струму на виході джерела струму протилежні.
, причому в контурі між точками і-0 напрямки струму резистора та струму на виході джерела струму протилежні.
Текст
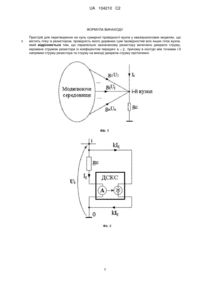
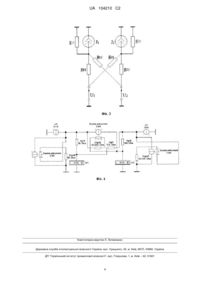
Реферат: Пристрій належить до області аналогової обчислювальної техніки та може бути використаний у побудові аналогових і квазіаналогових електричних моделюючих середовищ. В результаті застосування пристрою можуть бути створені нові електричні схеми для моделювання лінійних алгебраїчних об'єктів. Технічним результатом є усунення квазівід'ємних опорів. UA 104210 C2 (12) UA 104210 C2 UA 104210 C2 5 Винахід належить до області аналогової обчислювальної техніки та може бути використаний у побудові аналогових і квазіаналогових електричних моделюючих середовищ. Нехай фрагмент модельованого об'єкта в і-й точці описується рівнянням ai1 x1 ai2 x 2 ... aij xi ... ain xn bi 0 . (1) На фіг. 1 показано моделююче середовище, що має n вузлів і яке повинно моделювати фрагмент, що описується системою рівнянь (1). Для кожного і-го вузла фіг. 1 можна записати рівняння: g i1 ... g ij ... g in g i0 Ui g i1 U1 ... g ij U j ... g in Un I i 0 , (2) де j 1 n ; n - кількість сусідніх із і-им вузлів; gij - провідність між і-им і j-им вузлами; U 10 вузлова напруга; I - струм. Порівняння (1) і (2) показує, що рівняння (2) може описувати модель рівняння (1), якщо покласти g i1 g i2 ... g ij ... g in g i0 0 . (3) Це можливо, якщо g i 0 g i1 g i2 ... g ij ... g in . (4) Введемо в (2) масштабні залежності: U j x j x ; I i bib ; g ij a ijb / x , j 1 n . (5) З урахуванням співвідношення (4) після перетворень отримаємо вираз, еквівалентний виразу (1): g i1 U1 ... g ij Ui ... g in Un I i 0 a i1 x1 a i2 x 2 ... a ij xi ... a in xn b i 0 . 15 40 Відомий пристрій [1, 433; 2, 437], що реалізує вираз (4), який для перетворення на нуль сумарної провідності вузла містить гілку з резистором, провідність якого дорівнює сумі провідностей всіх інших віток вузла і до якого підводиться напруга, вдвічі більша за падіння напруги на зазначеному резисторі у напрямку, протилежному падінню напруги. Таке підключення утворює ефект від'ємної провідності. В результаті сумарна провідність вузла стає нульовою. Однак, застосування таких квазірезисторів зумовлює необхідність ручного ітераційного врівноваження в моделі шляхом обертання численних верньєрів (ролерів) настройки, що відповідно ускладнює процес побудови квазіаналога. Цей пристрій взято за прототип. В основу винаходу поставлена задача ліквідувати квазівід'ємні опори у квазіаналогових моделях і недоліки, пов'язані із ними, зокрема отримати можливість задавати параметри елементів моделі з клавіатури комп'ютера. Поставлена задача вирішується тим, що для утворення від'ємної провідності (4), а відповідно і для перетворення на нуль сумарної провідності вузла (3) паралельно зазначеній додатній провідності включено джерело струму, кероване струмом (ДСКС) провідності із коефіцієнтом передачі k=2, причому напрямки струмів протилежні. На фіг. 2 наводиться схема пристрою, що перетворює на нуль сумарну провідність вузла. Вона складається із провідності gi0, струм якої Ig як керуючий подається на джерело струму, кероване струмом (ДСКС). Із виходу ДСКС струм kIg надходить на провідність gi0 у напрямку, протилежному Ig. Схема фіг. 2 реалізується в середовищі програного комплексу Electronics WorkBench [3], який дозволяє задавати параметри елементів моделі у діалогових вікнах. Розглянемо чому дорівнюватиме провідність пристрою між точками і-0. Струм у провідності Ig після введення струму kIg дорівнює Ig-kIg=Ig(1-k), оскільки ці струми направлені зустрічно. Тоді значення провідності gi0 складатиме: Ig 1 k (6) gi 0 g i 0 1 k . U Із (6) випливає, що при k=2, gi 0 g i 0 . Цим вирішується поставлена задача. Зауважимо, 45 що заявлений пристрій може бути використаний як регульована коефіцієнтом k додатна і від'ємна провідність в межах, що визначаються виразом (6). При k > 1 провідність від'ємна; при k=1 провідність нульова; при k < 1 провідність додатна. Як приклад використання зазначеного пристрою наведемо реалізацію квазіаналогової моделі деякого лінійного алгебраїчного об'єкту, що описується системою рівнянь: 20 25 30 35 5 x1 3 x 2 1 (7) 8 x1 x 2 19 Цій системі відповідає електрична квазіаналогова модель, що представлена на фіг. 3. 1 UA 104210 C2 При g 10 g 11 g 12 та g 20 g 21 g 22 схема описується рівняннями: g 11U1 g 12U2 J1 (8) g 21U1 g 22U2 J2 Встановимо зв'язок між рівняннями (7) і (8), для чого введемо масштабні залежності Ui xi x ; Ji b b у систему (8). В результаті будемо мати: g 11 x x1 g 12 b x x 2 b1 b g 21 x x1 g 22 x x 2 b2 b b Із порівняння (7) і (9) виходить: a ij g ij x або g ij a ij b , де x , b - масштабні коефіцієнти. b x 5 (9) Тут: x Вольт ; b Ампер ; a b Сименс . одиниця х одиниця b x одиниця а Використовуючи наведені співвідношення підрахуємо параметри схеми, що наведена на фіг. 3: Сим 1. Вибираємо масштаб a b 0,01 . Тоді: g ij a ij a 0,01a ij . x одиниця а 10 А 2. Обираємо масштаб b 0,1 і отримуємо: J1=0,1 A; J2=1,9 A. одиниця b В 3. Знаходимо масштаб x b 0,1 10 . a 0,01 одиниця х 4. Знаходимо параметри елементів електричної моделі: g 11 a 11 a 5 0,01 0,05 Сим ; g 12 a 12 a 0,03 Сим ; g 10 g 11 g 12 0,02 Сим . 15 20 25 30 g 21 0,08 Сим ; g 22 0,01 Сим ; g 20 g 21 g 22 0,09 Сим . , J1 b b1 1 0,1 0,1A; J2 b b2 19 0,1 19 A . Застосуємо замість елементів моделі g10 та g20, що мають від'ємні провідності (схема моделі на фіг. 3), пропонований пристрій для перетворення на нуль сумарної провідності вузла. Схема реалізації моделі в середовищі WorkBench із відповідними параметрами і результати рішення у вольтах наведені на фіг. 4. Від'ємна провідність g12, що відповідає коефіцієнту а12 вихідної системи, також реалізована зазначеним способом. Результати моделювання співпадають із точним рішенням: U1=20 В; U1=30 В або x1 U1 20 2 ; x 2 30 3 . 10 x 10 Відзначимо, що кропіткий етап ручного ітераційного врівноваження у цьому випадку відсутній, а параметри елементів моделі введені як властивості використаних елементів із бібліотеки WorkBench за допомогою клавіатури комп'ютера. Джерела інформації: 1. Г.Е. Пухов. Методы анализа и синтеза квазианалоговых электронных цепей. - К.: Наукова думка, 1967. - 568 с. 2. Энциклопедия кибернетики: в 2 т. Т. 1. Абс - Мир / ред. В.М. Глушков [та ін.]. - К.: УСЭ, 1974. - 608 с. 3. Электротехника и электроника в экспериментах и упражнениях: Практикум на Electronics Workbench: в 2 т. / ред. Д.И. Панфилов. - М: Изд-во "Додека", 1999. 2 UA 104210 C2 ФОРМУЛА ВИНАХОДУ 5 Пристрій для перетворення на нуль сумарної провідності вузла у квазіаналогових моделях, що містить гілку із резистором, провідність якого дорівнює сумі провідностей всіх інших гілок вузла, який відрізняється тим, що паралельно зазначеному резистору включено джерело струму, кероване струмом резистора із коефіцієнтом передачі k 2 , причому в контурі між точками і-0 напрямки струму резистора та струму на виході джерела струму протилежні. 3 UA 104210 C2 Комп’ютерна верстка Л. Литвиненко Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601 4
ДивитисяДодаткова інформація
Автори англійськоюKandakov Hennadii Vasyliovych, Kryvenko Viktor Ivanovych
Автори російськоюКандаков Геннадий Васильевич, Кривенко Виктор Иванович
МПК / Мітки
МПК: G06G 7/122, H03H 5/00
Мітки: квазіаналогових, моделях, вузла, нуль, сумарної, провідності, пристрій, перетворення
Код посилання
<a href="https://ua.patents.su/6-104210-pristrijj-dlya-peretvorennya-na-nul-sumarno-providnosti-vuzla-u-kvazianalogovikh-modelyakh.html" target="_blank" rel="follow" title="База патентів України">Пристрій для перетворення на нуль сумарної провідності вузла у квазіаналогових моделях</a>
Попередній патент: Система для виробництва заповненої пластикової ємності та спосіб отримання такої пластикової ємності (варіанти)
Наступний патент: Штам бактерій rhizobium phaseoli для інокуляції насіння спаржевої квасолі
Випадковий патент: Установка для електрошлакового наплавлення рідким металом композитних валків