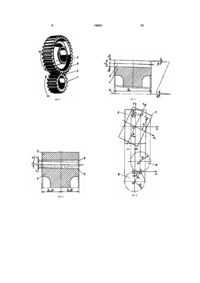
Евольвентна зубчаста передача з точковим контактом зубів
Номер патенту: 16691
Опубліковано: 15.08.2006
Формула / Реферат
Зубчаста передача, що складається із ведучого зубчастого колеса з криволінійними твірними бічних поверхонь зубів і веденого зубчастого колеса з прямолінійними твірними бічних поверхонь зубів, які утворюють між собою точковий контакт, яка відрізняється тим, що ведуче зубчасте колесо виконано у вигляді зрізаного конуса з кутом ділильного конуса ![]() , на твірній поверхні якого нарізані зуби, при цьому висота зубів
, на твірній поверхні якого нарізані зуби, при цьому висота зубів ![]() , висота головок
, висота головок ![]() , висота ніжок
, висота ніжок ![]() , а кут
, а кут ![]() визначається шляхом розв’язування трансцендентного рівняння
визначається шляхом розв’язування трансцендентного рівняння
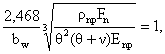
де ![]() - довжина зубів;
- довжина зубів; ![]() - приведений радіус кривизни спряженої пари зубів у полюсі зачеплення;
- приведений радіус кривизни спряженої пари зубів у полюсі зачеплення; ![]() - радіуси кривизни евольвентних кривих бічних профілів зубів у полюсі зачеплення ведучого та веденого зубчастих коліс; знак
- радіуси кривизни евольвентних кривих бічних профілів зубів у полюсі зачеплення ведучого та веденого зубчастих коліс; знак ![]() приймається при зовнішньому, а знак “-” при внутрішньому зачепленні зубів;
приймається при зовнішньому, а знак “-” при внутрішньому зачепленні зубів; ![]() - модуль зачеплення;
- модуль зачеплення; ![]() - числа зубів ведучого та веденого зубчастих коліс;
- числа зубів ведучого та веденого зубчастих коліс; ![]() - кут зачеплення;
- кут зачеплення; ![]() - нормальна сила, що діє на спряжену пару зубів;
- нормальна сила, що діє на спряжену пару зубів; ![]() - коефіцієнт Пуассона;
- коефіцієнт Пуассона; ![]() - приведений модуль пружності;
- приведений модуль пружності; ![]() - модулі пружності матеріалів зубчастих коліс.
- модулі пружності матеріалів зубчастих коліс.
Текст
Зубчаста передача, що складається із ведучого зубчастого колеса з криволінійними твірними бічних поверхонь зубів і веденого зубчастого колеса з прямолінійними твірними бічних поверхонь зубів, які утворюють між собою точковий контакт, яка відрізняється тим, що ведуче зубчасте колесо виконано у вигляді зрізаного конуса з кутом ділильного конуса , на твірній поверхні якого нарізані зуби, при цьому висота зубів h 2,25m b W θ , висота головок 3 16691 криволінійними твірними бічних поверхонь зубів і веденого зубчастого колеса з прямолінійними твірними бічних поверхонь зубів, які утворюють між собою точковий контакт, ведуче зубчасте колесо виконано у вигляді усіченого конуса з кутом ділильного конуса , на твірній поверхні якого нарізані зуби, при цьому висота зубів h=2,25m+bw , висота голівок ha=m+bw /2, висота ніжок hf=1,25(m+bw /2), а кут визначається шляхом вирішення трансцендентного рівняння 2,468 3 bw npFn 2 ( 1 , )Enp де bw - довжина зубів; np 1 2 /( 2 1) приведений радіус кривизни спряженої пари зубів у полюсі зачеплення; 1 mz1 sin w / 2, радіуси кривизни евольвентних кривих бічних профілів зубів у полюсі зачеплення ведучого та веденого зубчастих колес; знак «+» приймається при зовнішньому, а знак «-» при внутрішньому зачепленні зубів; m - модуль зачеплення; z1 z2 числа зубів ведучого та веденого зубчастих колес; dw - кут зачеплення; Fn - нормальна сила, що діє на спряжену пару зубів; - коефіцієнт Пуассона; Еnp=2Е1Е2/(Е1+Е2) - приведений модуль пружності; Е1, Е2 - модулі пружності матеріалів зубчастих колес. Порівняльний аналіз з прототипом показує, що зубчаста передача, яка заявляється, відрізняється тим, що ведуче зубчасте колесо виконано у вигляді усіченого конуса з кутом ділильного конуса , на твірній поверхні якого нарізані зуби, при цьому висота зубів h=2,25m+bw , висота голівок h=2,25m+bw /2, висота ніжок hf=1,25(m+bw /2, а кут визначається шляхом вирішення знайденого трансцендентного рівняння де bw - довжина зубів; m - модуль зачеплення. Порівняння технічного рішення, що заявляється, не тільки з прототипом, але й з іншими технічними рішеннями в даній галузі техніки, не виявило в них ознак, які б відрізняли технічне рішення, що заявляється, від прототипу, а це дозволяє зробити висновок про відповідність критерію «винахідницький рівень». На Фіг.1 зображена одноступінчата зубчаста передача зовнішнього зачеплення; на Фіг.2 ведуче зубчасте колесо у вигляді усіченого конуса; на Фіг.3 - ведене зубчасте колесо; на Фіг.4 розрахункова модель контакту спряженої пари зубів у вигляді циліндрів, повернутих відносно один одного на кут ; на Фіг.5 - радіуси вказаних циліндрів; на Фіг.6 - контакт спряженої пари зубів до навантаження у площині z0x; на Фіг.7 - дотик спряженої пари зубів у площині z0x після навантаження; на Фіг.8 - дотик спряженої пари зубів у площині z0y до навантаження; на Фіг.9 дотик спряженої пари зубів у площині z0y після навантаження. У відповідності з Фіг.1-9 маємо наступні позначення: 1, 2 - кутові швидкості ведучого та 2 mz 2 sin w /2 4 веденого зубчастих колес; h - висота зуба; ha висота голівки зуба; hf - висота ніжки зуба; bw довжина зубів; - кут ділильного конуса; с радіальний зазор між зубами; 1, 2 - радіуси циліндрів; х, у - поточні координати; b0, bk - мала і велика піввісь еліпсів; S(b0), S(bk) - максимальні переміщення зубів у площинах z0x і z0y при дії навантаження; Wmax=(SB0)=S(bk) - максимальна величина деформації спряженої пари зубів; - радіуси еквівалентних циліндрів у O1, O 2 площині z0y. Зубчаста передача складається з ведучого 1 та веденого 2 зубчастих колес з розташованими на них евольвентними зубами відповідно 3 і 4. При цьому ведуче зубчасте колесо виконано у вигляді усіченого конуса, твірна бічної поверхні якого складає кут з віссю 5 обертання даного колеса. У зв’язку із сказаним зуби 3 ведучого зубчастого колеса 1 мають кут нахилу в відносно вісі обертання 5. Для збереження нормального бічного зазору с=0,25m між зубами 3 та 4 при зачепленні висота зубів h, висота голівок ha і висота ніжок hf збільшені на величини відповідно bw , bw /2 і 1,25bw /2. Контакт зубів 3 та 4 зубчастих колес 1 та 2 умовно замінено моделлю контакту циліндрів 6 та 7, повернених відносно один одного на кут . Перерізи 8 та 9 вказаних циліндрів характеризуються кривими 10 та 11 з радіусами кривизни 1 та 2 , які в результаті деформації спряженої пари зубів 3 та 4 визначають еліпс 12 контактних деформацій у площині z0x. Твірні 13 та 14 бічних поверхонь зубів 3 та 4 з радіусами кривизни та при навантаженні O1 O2 визначають еліпс 15 контактних деформацій у площині z0y. Розглянемо короткий виклад рішення просторової контактної задачі стосовно до вказаної зубчастої передачі з метою визначення і порівняння її навантажувальної здатності з навантажувальною здатністю традиційної евольвентної зубчастої передачі. Рішення задачі виконаємо на основі методології теоретичних досліджень пружно зжатих тіл з початковим лінійним або точковим контактом, розробленої проф. А.П. Поповим. Функція контактних деформацій у площині z0x (Фіг.6 та 7) має вигляд W( x) Wmax 1 x2 2 b0 , (1) де b0 - мала піввісь еліпса; Wmax=b20/2 np максимальна величина контактної деформації при х=0; - приведений радіус np 1 2 /( 2 1) кривизни евольвентних зубів у полюсі зачеплення; mz 2 sin w / 2 - радіуси 1 mz1 sin w / 2 , 2 кривизни евольвентних кривих бічних профілів зубів у полюсі зачеплення ведучого та веденого зубчастих колес; z1, z2 - числа зубів ведучого та веденого зубчастих колес; m - модуль зачеплення; 5 16691 w - кут зачеплення; знак «+» приймається при зовнішньому, а знак «-» при внутрішньому зачепленні зубів. Для визначення функції W(y) у площині z0y звернемося до Фіг.4, із якої слідує, що при повороті циліндра 7 відносно циліндра 6 на кут тачка a прийме положення точки b, тоді, виходячи з малої величини кута , отримаємо ab ytg y , (2) де y - поточна координата. При повороті циліндра 7 відносно циліндра 6 центр його кола зміститься у положення точки О1 на величину ab=Ос. З Фіг.5 очевидно, що mn ab y , sin O2n O2n 2 де - кут укладений між відрізками О2m і О2n. Вважаючи sin = через малу величину кута 2, запишемо y , (3) 6 де - приведений O O1 O2 /( O2 O1) радіус кривизни еквівалентних циліндрів у точці контакту. Рівняння (7) характеризує форму зазору у напрямку вісі у між еквівалентними циліндрами. Тоді, виходячи з еліптичного закону змінення контактних напружень у напрямку вісі у, уявимо функцію W(y) у наступному вигляді S1( y ) 2 cos 2 2 (1 cos ) 2 (1 cos y ) . (4) 2 Розклавши функцію cos(y / 2 у ) ряд, вважаючи, що величина y / 2 є величиною малого порядку, визначимо вираження y y2 2 . 2 2 2 З урахуванням останньої залежності вираз (4) прийме вигляд cos 1 2 S1( y ) де O1 циліндра 7. 2/ 2 радіус еквівалентного Якщо циліндр 6 повернути на кут за годинниковою стрілкою до збігання його з положенням циліндра 7, а потім знов вернути у початкове положення, то у цьому випадку, за аналогією з функцією (5), знайдемо вираження S2 ( y ) y2 2 , (6) S1( y ) S2 ( y ) y2 , (7) 2 O bKm b 0 B ( x, y )dxdy bKm b 0 BFn 1 2 2b0Fn Enp 1 x2 2 b0 1 y2 2 bK 2 np 2 bK 1 x2 1 2 b0 y2 . (9) 2 bK При х=0 та у=0 функції (1) та (8) мають однакові значення максимальних контактних деформацій, у зв’язку із чим запишемо 2 b0 2 np 2 b bK 2 або 0 bK 2 np . Ділянка контакту зубів у даній задачі являє собою ділянку еліпса розміром b0bk, де b0, bk мала і велика піввісі еліпса. Для інтегрування у подальшому функції (9) замінимо ділянку еліпса еквівалентною за величиною ділянкою прямокутника зі сторонами 2b0 та 2bKm. Виходячи з рівняння b0bk=4b0bKm, знайдемо bK . (10) bKm 4 З урахуванням заміни параметра bK параметром bKm функція (9) прийме вигляд W ( x, y ) 2 b0 2 np 1 x2 1 2 b0 y2 2 bKm 2 np 2 bKm 1 x2 2 b0 y2 1 . (11) 2 bKm Для знаходження другої функції W(x,y) скористаємося узагальненим законом Гука та гіпотезою Вінклера. У зв’язку із цим, виходячи із підпорядкування тіл, що зближуються, у межах пружності гіпотезі Вінклера, запишемо W( x, y) B ( x, y) , (12) де ( x, y) - функція контакту напружень; В коефіцієнт подушки, що виміряється у м3/H. При однакових значеннях коефіцієнта Пуассона та E1 E2 коефіцієнт 1 2 подушки для задачі, що розглядається, має вигляд O2 2 де - радіус еквівалентного O2 1/ циліндра 6. На основі виражень (5) та (6) отримаємо функцію S( y ) 2 b0 2 np W ( x, y ) 2 y , (5) 2 O1 2 bK 2 y2 1 2 , (8) 2 np bK Враховуючи, що максимальні значення функцій (1) та (8) співпадають при х=у=0, перейдемо від функцій W(x) та W(у) до єдиної функції 2 Позначивши величину відрізка Оm=cm через S1(y), знайдемо з урахуванням виразу (3) наступне рівняння 2 bK y2 1 2 2 O bK W( y) B 2 1 2b0 , (13) Enp де Еnp=2Е1E2/(Е1+E2) - приведений модуль пружності; Е1, Е2 - модулі пружності матеріалів. На підставі залежностей (11), (12) та (13) запишемо рівняння об’ємного напруженодеформованого стану тіл 2 b0 2 np bKm b 0 1 bKm b 0 x2 2 b0 1 y2 2 bKm dxdy 2 3 b0bKm 8 np . 7 16691 Виразивши у останньому рівнянні параметр bKm через праву частину рівняння (10), знайдемо залежність b0 1 2363 , Fn . (14) )E ( Вважаючи bK=bo/ , великої піввісі еліпса bK 1,2343 Fn 2 ( )E запишемо вираження . (15) З урахуванням виразів (11)-(14) отримаємо залежність максимальних контактних напружень max 0,3393 ( )2 E2nF 2 np . (16) Рівняння (14)-(16) містять невідомий кут , у зв’язку із чим для їх рішення необхідно знайти додаткове рівняння. З цією метою, прийняв bK=bW/2 у виразі (15) і поділивши ліву і праву частини вказаного виразу на bW/2, отримаємо трансцендентне рівняння 2,468 3 bW npFn 2 ( 1. (17) )Enp Кут , знайдений шляхом вирішення рівняння (17), є оптимальним, так як він характеризує граничну величину 2bK великої вісі еліпса, що дорівнює довжині зубів bW. Для оцінки ефективності запропонованого технічного рішення виконаємо розрахунок зубчастої передачі зовнішнього зачеплення, у якої z1=44; z2=66; m=5мм; W =20°; bW=150мм; у=0,3; E=2,1∙105MПa; Fn=4∙104H. За приведеною формулою знаходимо np =22,573мм, а за формулами Герца визначаємо максимальні контактні напруження H =666МПа і напівширину прямокутної ділянки дотику b0=0,255мм. Потім, задавшись значеннями =(5...20)∙10-3рад, визначимо шляхом графоаналітичного рівняння (17) кут =7,9∙103 рад. Виходячи з кута =7,9∙10-3рад за формулами (14)-(16) визначимо b0=0,593мм; bK=bW/2=75мм та max =466МПа. Таким чином, внаслідок повороту зубів 3 ведучого зубчастого колеса 1 на кут =7,9∙10-3рад відносно вісі обертання 5 максимальні контактні напруження знизилися у max / H =666/466=1,428 рази, у зв’язку із чим навантажувальна здатність зачеплення по контактним напруженням підвищилась у 1,4283=2,914 рази. Вказане зниження контактних напружень при -3 повороті зубів на кут =7,9∙10 рад обумовлено тим, що ділянка дотику при цьому b0bK=3,14∙0,593∙75=139,6мм оказалась більше 8 ділянки контакту 2b0bW=2∙0,255∙150=76,5мм2 при =0° у 139,6/76,5=1,518 рази. Приведені дані розрахунку вказують на високу навантажувальну здатність запропонованої зубчастої передачі, яка суттєво перевищує навантажувальну здатність не тільки існуючих евольвентних зубчастих передач, але й передач Новікова. Крім того, у запропонованій зубчастій передачі відсутня концентрація навантаження на торцевих ділянках зубів. Ці передачі у набагато меншій ступені підпадають під вплив неточностей виготовлення зубів, деформацій і расцентровок вісей зубчастих колес на працездатність зачеплення. Слід також відмітити покращені віброакустичні характеристики передачі внаслідок більш плавного входу зубів у зачеплення і наявності між зубами підвищених товщин мастильних шарів. Запропонована зубчаста передача базується на технології виготовлення зубів 3 ведучого зубчастого колеса 1, властивої широко розповсюдженої технології виготовлення прямозубих конічних колес. Зубчаста передача працює наступним чином. При передачі від двигуна на ведуче зубчасте колесо 1 обертового моменту останнє починає обертатися з кутовою швидкістю 1 . При цьому зуб 3 ведучого зубчастого колеса 1 впливає на зуб 4 веденого зубчастого колеса 2, у зв’язку із чим останнє набуває кутову швидкість 2 , яка передається виконавчому механізму, навантажуючи його обертовим моментом. У процесі навантаження вказаних зубів точковий контакт у двох взаємноперпендикулярних площинах z0x та z0y (Фіг.6 та 8, точка 0) перетворюється у ділянку контакту розміром b0bK, де b0, bK - мала та велика піввісі еліпсів 12 та 15 (Фіг.7 та 9). При цьому довжина ділянки контакту 2bK буде дорівнювати довжині зубів bW. Вказане розташування зубів 3 та 4 відносно один одного (Фіг.3), що характеризується кутом повороту >00, дозволяє отримати при роботі зубчастої передачі розміри ділянки контакту кожної із спряжених пар зубів, перевищуючої такі при =0°, що і забезпечує запропонованій зубчастій передачі високу навантажувальну здатність. Економічний ефект від впровадження запропонованого технічного рішення варто очікувати за рахунок підвищення навантажувальної здатності та ефективності роботи зубчастої передачі. Суспільна корисність технічного рішення, що заявляється, полягає в поліпшенні віброакустичих характеристик зачеплення внаслідок зниження шуму і вібрацій (промсанітарія). 9 16691 10 11 Комп’ютерна верстка А. Рябко 16691 Підписне 12 Тираж 26 прим. Міністерство освіти і науки України Державний департамент інтелектуальної власності, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601
ДивитисяДодаткова інформація
Назва патенту англійськоюEvolvent tooth gear with point contact of teeth
Автори англійськоюPopov Oleksii Pavlovych
Назва патенту російськоюЭвольвентная зубчатая передача с точечным контактом зубцов
Автори російськоюПопов Алексей Павлович
МПК / Мітки
МПК: F16H 1/00
Мітки: контактом, передача, зубчаста, евольвентна, точковим, зубів
Код посилання
<a href="https://ua.patents.su/6-16691-evolventna-zubchasta-peredacha-z-tochkovim-kontaktom-zubiv.html" target="_blank" rel="follow" title="База патентів України">Евольвентна зубчаста передача з точковим контактом зубів</a>
Попередній патент: Спосіб одержання біохімічно активної води
Наступний патент: Прокатна кліть
Випадковий патент: Шпала залізобетонна