Спосіб розгортання зв’язки космічних тіл з приведенням її до місцевої вертикалі
Номер патенту: 99303
Опубліковано: 25.05.2015
Автори: Алпатов Анатолій Петрович, Закржевський Олександр Євгенович, Ткаченко Ярослав Володимирович
Формула / Реферат
Спосіб розгортання зв'язки космічних тіл з приведенням її до місцевої вертикалі, при якому розстиковують обидва об'єкта зв'язки шляхом надання їм початкової швидкості вздовж місцевої вертикалі за допомогою пружинного штовхача і випускають нитку з пригальмовуванням, для забезпечення її натягу, до деякої довжини випущеної нитки ![]() , яка менше проектної довжини зв'язки, який відрізняється тим, що після входження зв'язки в режим маятникових коливань відносно місцевої вертикалі в площині орбіти, починаючи з моменту часу
, яка менше проектної довжини зв'язки, який відрізняється тим, що після входження зв'язки в режим маятникових коливань відносно місцевої вертикалі в площині орбіти, починаючи з моменту часу ![]() відхилення зв'язки на максимальний кут у від'ємному напрямку, випускають нитку за законом
відхилення зв'язки на максимальний кут у від'ємному напрямку, випускають нитку за законом
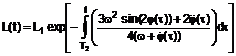 ,
,
де ![]() - кутова швидкість руху центру мас зв'язки по круговій орбіті навколо Землі,
- кутова швидкість руху центру мас зв'язки по круговій орбіті навколо Землі, ![]() - бажаний закон зміни в часі кута між поздовжньою віссю зв'язки та місцевою вертикаллю, який задовольняє умовам
- бажаний закон зміни в часі кута між поздовжньою віссю зв'язки та місцевою вертикаллю, який задовольняє умовам ![]() , що забезпечує для закону
, що забезпечує для закону ![]() програмної зміни довжини нитки, що випускається, плавне завершення випуску нитки до проектної довжини в момент приведення зв'язки, що розгортається, до місцевої вертикалі, що дозволяє уникнути виникнення її поздовжніх коливань,
програмної зміни довжини нитки, що випускається, плавне завершення випуску нитки до проектної довжини в момент приведення зв'язки, що розгортається, до місцевої вертикалі, що дозволяє уникнути виникнення її поздовжніх коливань, ![]() - час закінчення розгортання зв'язки
- час закінчення розгортання зв'язки ![]() , який визначають з умови
, який визначають з умови
![]() ,
,
де ![]() - проектна довжина випущеної нитки.
- проектна довжина випущеної нитки.
Текст
Реферат: Спосіб розгортання зв'язки космічних тіл з приведенням її до місцевої вертикалі, при якому розстиковують обидва об'єкта зв'язки шляхом надання їм початкової швидкості вздовж місцевої вертикалі за допомогою пружинного штовхача і випускають нитку з пригальмовуванням, для забезпечення її натягу, до деякої довжини випущеної нитки L 1 , яка менше проектної довжини зв'язки. Після входження зв'язки в режим маятникових коливань відносно місцевої вертикалі в площині орбіти, починаючи з моменту часу t T2 відхилення зв'язки на максимальний кут у від'ємному напрямку, випускають нитку за законом t 3 2 sin( 2( )) 2( ) L( t ) L1 exp d , 4( ( )) T 2 де - кутова швидкість руху центру мас зв'язки по круговій орбіті навколо Землі, (t ) бажаний закон зміни в часі кута між поздовжньою віссю зв'язки та місцевою вертикаллю, який задовольняє умовам (T2 ) 0 , (T2 ) ( t F ) ( t F ) ( t F ) 0, (T2 ) 3 / 2 2 sin( 2(T2 )) , що забезпечує для закону L(t ) програмної зміни довжини нитки, що випускається, плавне завершення випуску нитки до проектної довжини в момент приведення зв'язки, що розгортається, до місцевої вертикалі, що дозволяє уникнути виникнення її поздовжніх коливань, t F - час закінчення розгортання зв'язки ((t F ) 0) , який визначають з умови L(t F ) LF , де L F - проектна довжина випущеної нитки. UA 99303 U (54) СПОСІБ РОЗГОРТАННЯ ЗВ'ЯЗКИ КОСМІЧНИХ ТІЛ З ПРИВЕДЕННЯМ ЇЇ ДО МІСЦЕВОЇ ВЕРТИКАЛІ UA 99303 U UA 99303 U 5 10 15 20 25 30 35 40 45 50 55 Корисна модель належить до космічної техніки, а саме до космічних тросових систем (КТС), і може знайти застосування при розгортанні зв'язок космічних тіл. Серед проблем, пов'язаних із створенням КТС, особливе місце займає проблема розгортання зв'язки двох космічних об'єктів в задане положення. У практиці застосування КТС їх найбільш затребувана конфігурація на орбіті така, при якій центр гравітації системи рухається по круговій орбіті і в'язь розташована вздовж місцевої вертикалі. Для сталої довжини в'язі ця вертикальна конфігурація - стійка відносна рівновага системи в орбітальному базисі. Теоретично, це вимагає абсолютно сферичної Землі. В межах технічної точності це припущення можна вважати виконаним. При зміні довжини в'язі конфігурація вздовж місцевої вертикалі втрачає свою стійкість відповідно до теореми про зміну моменту кількості руху механічної системи [1]. Важлива експлуатаційна вимога, щоб зв'язка в результаті розгортання або згортання виявилася на місцевій вертикалі, може бути задоволена тільки при керуванні її рухом. Відомий спосіб розгортання орбітальних тросових систем, що передбачає випуск троса з регулюванням швидкості його випуску [2]. Недоліком цього способу є те, що при такому керуванні випуском троса неможливо здійснити гасіння поздовжніх коливань зв'язки, що виникають внаслідок пружності троса. Збільшення інтенсивності поздовжніх коливань здатне привести до повного ослаблення троса, що в свою чергу може викликати перебої в роботі пристроїв його випуску. Відомі способи розгортання орбітальних тросових систем, що передбачають випуск троса з регулюванням сили його натягу. Один з таких способів [3] прийнятий авторами як прототип. Цей спосіб передбачає розгортання зв'язки в три етапи. На першому етапі об'єктам надають достатню швидкість розходження вздовж місцевої вертикалі і регулюють натяг троса, а при переході до другого етапу хоча б одному об'єкту надають додаткову швидкість, що забезпечує нульову горизонтальну швидкість розходження об'єктів і задану вертикальну швидкість розходження, яка потім зберігається при певному законі регулювання натягу троса. Перехід до третього етапу виконують при довжині троса, меншій заданої кінцевої довжини на величину, пропорційну швидкості вертикального розходження об'єктів, пригальмовують випуск троса і припиняють його після того, як довжина троса хоча б раз перевищить задану кінцеву, в момент, коли швидкість випуску, стане менше величини, яка визначається допустимою амплітудою залишкових коливань сили натягу троса. Недоліком такого способу є складність практичної реалізації регулювання сили натягу слабонатягнутого троса, що випускається. В основу корисної моделі поставлена задача розгортання зв'язки космічних тіл з приведенням її до місцевої вертикалі є знаходження закону зміни довжини нитки, що випускається, який забезпечить бажаний закон зміни кута між зв'язкою та місцевої вертикаллю, а при досягненні проектної довжини - співпадіння зв'язки з місцевою вертикаллю з нульовим кутом відхилення від вертикалі і нульовою кутовою швидкістю. Технічним результатом є приведення зв'язки до місцевої вертикалі по наперед заданому закону з плавним завершенням процесу, що дозволяє уникати поздовжніх коливань нитки. Поставлена задача вирішується тим, що на першому етапі проводять розстиковку двох об'єктів зв'язки шляхом надання їм початкової швидкості вздовж місцевої вертикалі за допомогою пружинного штовхача, випускають нитку з пригальмовуванням, для забезпечення її натягу, до деякої довжини L 1 , яка менше проектної довжини зв'язки L F . Після завершення першого етапу зв'язка входить в режим маятникових коливань відносно місцевої вертикалі в площині орбіти. Другий етап розгортання починають в момент відхилення зв'язки на максимальний кут у від'ємному напрямку 0 . Позначимо цей момент часу T2 . Розглянемо як приклад рух зв'язки двох однакових тіл в орбітальному базисі, введеному згідно з [4], с. 15. Будемо вимагати, щоб кут між місцевою вертикаллю і зв'язкою, починаючи з моменту часу t T2 , змінювався по заданому закону (t ) . При русі зв'язки в площині орбіти вектор кінетичного моменту зв'язки в орбітальному базисі має вигляд K C 0,2r( t ) 2 m( ( t )),0 , де m - маса об'єкта зв'язки; - кутова швидкість руху центру мас зв'язки по круговій орбіті навколо Землі; r(t) L(t ) / 2 - половина довжини зв'язки. На зв'язку діє гравітаційний момент MC 0,3m2r 2 (t) sin2(t),0 . g Завдяки тому, що коливання відбуваються в площині орбіти, 1 UA 99303 U 5 KC 0 , і, згідно з теоремою про зміну кінетичного моменту механічної системи, має місце залежність dK C MC . g dt Після елементарних перетворень отримаємо звичайне диференціальне рівняння першого порядку з відповідною початковою умовою 3(2 sin 2 2) r r , r(T2 ) r0 L1 / 2 . 4( ) Звідки знаходимо 10 15 t 3 2 sin( 2( )) 2( ) L( t ) L1 exp d . 4( ( )) T 2 З точки зору плавного приведення зв'язки до місцевої вертикалі закон (t ) для другого етапу розгортання повинен задовольняти умовам (T2 ) 0 , (T2 ) ( t F ) ( t F ) ( t F ) 0, (T2 ) 3 / 22 sin( 2(T2 )) , виконання яких забезпечує плавний початок і таке ж завершення розгортання зв'язки. Ці умови забезпечують виконання умов r(T2 ) r(t F ) 0 . Як приклад, задамо закон зміни кута (t ) у вигляді полінома i t T2 ci t T , 2 i0 F де t F - час закінчення розгортання зв'язки, який визначається з умови L(t F ) LF ; (t ) 5 2 3 c 0 0 ; c 1 0; c 2 0.752 sin( 2 0 ); c 3 ( 10 0 2.252 t F sin( 2 0 )) / t F ; 20 25 30 35 2 4 2 5 c 4 (15 0 2.252 t F sin( 2 0 )) / t F ; c 5 ( 6 0 0.752 t F sin( 2 0 )) / t F . На фіг. 1 - фіг. 4 представлені графіки зміни в часі довжини випущеної нитки, кута між зв'язкою та місцевої вертикаллю, а також траєкторії тіл зв'язки в площині орбіти в орбітальному базисі відповідно для орбіти радіуса 7000 км, проектної довжини випущеної нитки 5000 м, довжини випущеної нитки після завершення першого етапу 4000 м і маси кожного тіла зв'язки 10 кг. Як видно з представлених графіків, в момент закінчення розгортання зв'язка розташована вздовж місцевої вертикалі. Чисельні дослідження також показали, що нитка натягнута протягом всього часу другого етапу розгортання, а в момент завершення розгортання відсутні скачки натягу нитки, що дозволяє уникнути поздовжніх коливань зв'язки. Джерела інформації: [1] Лурье А.И. Аналитическая механика. - М.: Физматгиз., 1961. - 824 с. [2] Левин Е.М. О развертывании протяженной связки на орбите // Космические исследования.-1983. - Т. XXI, вып. 1. - С. 678-688. [3] Патент на изобретение РФ № 2112715 Способ развертывания орбитальной тросовой системы, опубл. 10.06.1998. Собственник: Ракетно-космическая корпорация "Энергия" им. С.П. Королева. [4] Белецкий В. В. Движение искусственного спутника относительно центра масс. - М.: Наука, 1965. - 416 с. ФОРМУЛА КОРИСНОЇ МОДЕЛІ 40 45 Спосіб розгортання зв'язки космічних тіл з приведенням її до місцевої вертикалі, при якому розстиковують обидва об'єкта зв'язки шляхом надання їм початкової швидкості вздовж місцевої вертикалі за допомогою пружинного штовхача і випускають нитку з пригальмовуванням, для забезпечення її натягу, до деякої довжини випущеної нитки L 1 , яка менше проектної довжини зв'язки, який відрізняється тим, що після входження зв'язки в режим маятникових коливань відносно місцевої вертикалі в площині орбіти, починаючи з моменту часу t T2 відхилення зв'язки на максимальний кут у від'ємному напрямку, випускають нитку за законом 2 UA 99303 U t 3 2 sin( 2( )) 2( ) L( t ) L1 exp d , ( )) 4( T 2 де - кутова швидкість руху центру мас зв'язки по круговій орбіті навколо Землі, (t ) - бажаний закон зміни в часі кута між поздовжньою віссю зв'язки та місцевою вертикаллю, який задовольняє умовам (T2 ) 0 , (T2 ) ( t F ) ( t F ) ( t F ) 0, (T2 ) 3 / 2 2 sin( 2(T2 )) , що 5 10 забезпечує для закону L(t ) програмної зміни довжини нитки, що випускається, плавне завершення випуску нитки до проектної довжини в момент приведення зв'язки, що розгортається, до місцевої вертикалі, що дозволяє уникнути виникнення її поздовжніх коливань, t F - час закінчення розгортання зв'язки ((t F ) 0) , який визначають з умови L(t F ) LF , де L F - проектна довжина випущеної нитки. 3 UA 99303 U Комп’ютерна верстка Л. Ціхановська Державна служба інтелектуальної власності України, вул. Василя Липківського, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут інтелектуальної власності”, вул. Глазунова, 1, м. Київ – 42, 01601 4
ДивитисяДодаткова інформація
Автори англійськоюAplatov Anatolii Petrovych
Автори російськоюАлпатов Анатолий Петрович
МПК / Мітки
МПК: B64G 1/34
Мітки: тіл, зв'язки, розгортання, спосіб, космічних, приведенням, місцевої, вертикалі
Код посилання
<a href="https://ua.patents.su/6-99303-sposib-rozgortannya-zvyazki-kosmichnikh-til-z-privedennyam-do-miscevo-vertikali.html" target="_blank" rel="follow" title="База патентів України">Спосіб розгортання зв’язки космічних тіл з приведенням її до місцевої вертикалі</a>
Попередній патент: Спосіб лікування ендотеліальної дисфункції у хворих на артеріальну гіпертензію
Наступний патент: Опалювальна піч
Випадковий патент: Пристрій для рідинної обробки коренебульбоплодів










