Спосіб розрахунку результуючого моменту сили тяги всього комплексу м’язів на поверхні очного яблука людини
Номер патенту: 122980
Опубліковано: 12.02.2018
Автори: Ємченко Віктор Іванович, Голодний Роман Анатолійович, Юрко Олексій Олексійович, Коваль Вікторія Юріївна, Кухаренко Дмитро Володимирович, Кириченко Назар Дмитрович
Формула / Реферат
Спосіб розрахунку результуючого моменту сили тяги всього комплексу м'язів на поверхні моделі очного яблука людини, який полягає у тому, що визначають сферичні координати на моделі обох очних яблук, які являють собою сфери з визначеним радіусом у відповідності до виразів:
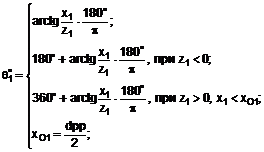
![]() ;
;
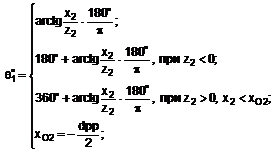
![]() ;
;
де ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() - декартові координати правого та лівого ока відповідно;
- декартові координати правого та лівого ока відповідно;
![]() ,
, ![]() ,
, ![]() ,
, ![]() - сферичні координати сфери правого та лівого ока відповідно.
- сферичні координати сфери правого та лівого ока відповідно.
![]() ,
, ![]() - координати правого та лівого ока відповідно з урахуванням відстані між центром очних яблук
- координати правого та лівого ока відповідно з урахуванням відстані між центром очних яблук ![]() , який відрізняється тим, що враховано зорову вісь іншого ока та моменти сил його групи м'язів, визначають момент сили м'яза відносно осей декартової системи координат у відповідності до виразів:
, який відрізняється тим, що враховано зорову вісь іншого ока та моменти сил його групи м'язів, визначають момент сили м'яза відносно осей декартової системи координат у відповідності до виразів:
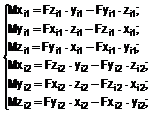
де: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() - проекції вектору сили тяги, що діє в i-й точці на осях
- проекції вектору сили тяги, що діє в i-й точці на осях ![]() ,
, ![]() та
та ![]() відповідно до кожного з очних яблук;
відповідно до кожного з очних яблук; ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() - моменти векторів сил тяги відносно відповідних осей після обертання.
- моменти векторів сил тяги відносно відповідних осей після обертання.
Текст
Реферат: Спосіб розрахунку результуючого моменту сили тяги всього комплексу м'язів на поверхні очного яблука людини полягає у тому, що визначають сферичні координати на моделі обох очних яблук, які являють собою сфери з визначеним радіусом у відповідності до виразів: x 180 ; arctg 1 z1 180 arctg x1 180 , при z 0; 1 z1 1 x 180 , при z1 0, x1 xO1; 360 arctg 1 z1 dpp xO1 ; 2 1 arctg y1 2 2 x1 z1 180 ; x 180 ; arctg 2 z2 180 arctg x 2 180 , при z 0; 2 z2 1 x 180 , при z2 0, x 2 xO2; 360 arctg 2 z2 dpp x O2 ; 2 UA 122980 U (12) UA 122980 U arctg 2 y2 x 2 z2 2 2 180 ; де x 1 , y 1 , z 1 , x 2 , y 2 , z 2 - декартові координати правого та лівого ока відповідно; 1 , 1 , 2 , 2 - сферичні координати сфери правого та лівого ока відповідно; x O1 , x O2 - координати x правого ті лівого ока відповідно з урахуванням відстані між центром очних яблук dpp . Враховано зорову вісь іншого ока та моменти сил його групи м'язів. Визначають результуючий момент сили ділянки прикріплення м'яза до поверхні очного яблука. UA 122980 U Спосіб розрахунку результуючого моменту сили тяги всього комплексу м'язів на поверхні очного яблука людини полягає у тому, що визначають сферичні координати на моделі, яка являє собою сферу з визначеним радіусом у відповідності до виразів: x 180 ; arctg z x 180 180 arctg , при z 0; z x 180 180 arctg , при z 0, x 0; z arctg 5 10 y x 2 z2 180 , де x , y , z - декартові координати; , - сферичні координати сфери. В комп'ютер вводять дані про тип м'язів, з можливістю визначити моменти сил цих м'язів, визначають момент сили м'яза відносно осей декартової системи координат у відповідності до виразів: Mxi Fyi zi Fzi yi ; Myi Fxi zi Fzi xi ; Mzi Fxi yi Fyi xi , 15 20 25 де, Fx i , Fy i , Fzi - проекції вектору сили тяги, що діє в i-й точці на осях OX , OY та OZ очного яблука; Mxi , Myi , Mzi - моменти векторів сил тяги відносно відповідних осей після обертання. Корисна модель належить до медицини, а саме до офтальмології, і може бути використана для підвищення ефективності хірургічних операцій і більш досконалого вивчення окорухових структур обох очних яблук людини. Аналогом даного способу є спосіб, який дає наочне представлення обертання моделі ока у тривимірній декартовій системі координат: [http://www.bausch-pharma.ru/dry_eye/fl/flashl.htm]. Недоліками аналога є неможливість автоматизовано проводити розрахунки, неможливість використання офтальмологічної сферичної системи координат, примітивність програмного забезпечення, а також тривимірне обертання, яке обмежене часом. Найближчим до корисної моделі є спосіб розрахунку моментів сил окорухових м'язів на поверхні моделі очного яблука [патент на корисну модель UA № 80907, А61В 3/00, G09B 23/28, опубл. 10.06.2013, бюл. 11], який полягає у тому, що визначають сферичні координати на моделі, яка являє собою сферу з визначеним радіусом у відповідності до виразів: x 180 ; arctg z x 180 180 arctg , при z 0; z x 180 360 arctg , при z 0, x 0; z arctg 30 y x 2 z2 180 , де x , y , z - декартові координати; , - сферичні координати сфери. Момент сили м'яза відносно осей декартової системи координат у відповідності до виразів: Mxi Fyi zi Fzi yi ; 35 Myi Fxi zi Fzi xi ; Mzi Fxi yi Fyi xi , де, Fx i , Fy i , Fzi - проекції вектору сили тяги, що діє в і-й точці на осях OX , OY та OZ очного яблука; 1 UA 122980 U Mxi , Myi , Mzi - моменти векторів сил тяги відносно відповідних осей після обертання. 5 10 Недоліками найближчого аналога є те, що не враховано зорову вісь іншого очного яблука, завдяки чому відновлення бінокулярного зору людини є неможливе. Корисна модель усуває вказані недоліки. Задача корисної моделі полягає в удосконаленні способу розрахунку моментів сил всього комплексу очних м'язів на поверхні моделі окорухового апарату людини, що заснований на визначенні результуючого моменту сили ділянки прикріплення м'яза до поверхні очного яблука. Поставлена задача вирішується у способі розрахунку результуючого моменту сили тяги всього комплексу м'язів на поверхні очного яблука людини, який полягає у тому, що визначають сферичні координати на моделі обох очних яблук, які являють собою сфери з визначеним радіусом у відповідності до виразів: x 180 ; arctg 1 z1 180 arctg x1 180 , при z 0; 1 z1 1 x 180 , при z1 0, x1 xO1; 360 arctg 1 z1 dpp xO1 ; 2 1 arctg y1 2 2 x1 z1 180 ; x 180 ; arctg 2 z2 180 arctg x 2 180 , при z 0; 2 z2 2 x 180 , при z 2 0, x 2 x O2 ; 360 arctg 2 z2 dpp x O2 ; 2 arctg 2 15 y2 x2 z2 2 2 180 ; де x1 , y1 , z1 , x 2 , y 2 , z 2 - декартові координати правого та лівого ока відповідно; 1 , 1 , 2 , 2 - сферичні координати сфери правого та лівого ока відповідно. xO1 , xO2 - координати правого та лівого ока відповідно з урахуванням відстані між центром очних яблук dpp . 20 25 Який відрізняється тим, що враховано зорову вісь іншого ока та моменти сил його групи м'язів. Визначають момент сили м'яза відносно осей декартової системи координат у відповідності до виразів: Mxi1 Fzi1 yi1 Fyi1 zi1; Myi1 Fx i1 zi1 Fzi1 xi1; Mzi1 Fy i1 xi1 Fxi1 yi1; Mxi2 Fzi2 yi2 Fy i2 zi2; My Fx z Fz x ; i2 i 2 i2 i2 i2 Mzi2 Fy i2 xi2 Fx i2 yi2; де, Fxi1 , Fyi1 , Fzi1 , Fxi2 , Fyi2 , Fzi2 - проекції вектору сили тяги, що діє в i-й точці на осях OX , OY та OZ відповідно до кожного з очних яблук; Mxi1 , Myi1 , Mzi1 , Mxi2 , Myi2 , Mzi2 - моменти векторів сил тяги відносно відповідних осей після обертання. 2 UA 122980 U 5 У способі використовують мову високого рівня програмування Delphi 7 і відповідний математичний апарат. Спільними ознаками найближчого аналога та корисної моделі є визначення сферичних координат на моделі, яка являє собою сферу з визначеним радіусом. Корисна модель відрізняється тим, що враховано зорову вісь іншого ока та моменти сил його групи м'язів. Визначають момент сили м'яза відносно осей декартової системи координат у відповідності до виразів: Mxi1 Fzi1 yi1 Fyi1 zi1; Myi1 Fx i1 zi1 Fzi1 xi1; Mzi1 Fy i1 xi1 Fxi1 yi1; Mxi2 Fzi2 yi2 Fy i2 zi2; My Fx z Fz x ; i2 i 2 i2 i2 i2 Mzi2 Fy i2 xi2 Fx i2 yi2; 10 де, Fxi1 , Fyi1 , Fzi1 , Fxi2 , Fyi2 , Fzi2 - проекції вектору сили тяги, що діє в i-й точці на осях OX , OY та OZ відповідно до кожного з очних яблук; Mxi1 , Myi1 , Mzi1 , Mxi2 , Myi2 , Mzi2 - моменти векторів сил тяги відносно відповідних осей після 15 20 25 30 35 обертання. На ілюстративному матеріалі представлений спосіб розрахунку моментів сил окорухових м'язів на поверхні моделі очного яблука. Спосіб здійснюють наступним чином: запускають файл розрахунку результуючого моменту сили окорухових м'язів. В першу чергу вводять у вікна під номером 1 та 2 радіуси моделей обох очей в міліметрах, які отримані за допомогою рентгенівської томографії. Якщо цього не зробити, не буде здійснений процес розрахунків. Далі у вікні 3 потрібно ввести відстань між центрами очних яблук в міліметрах. Спосіб дозволяє розраховувати момент сили м'яза у точках M та M ' відносно осей тривимірної декартової системи координат для кожного очного яблука. Для цього необхідно у вікні 4 обрати необхідне очне яблуко (праве або ліве), встановити на його поверхні фіксовану точку M , яка має червоний колір. За допомогою колеса маніпулятора типу "миша" обертають модель ока у необхідну позицію. За допомогою лівої клавіші встановлюють точку M ' , яка має жовтий колір, на поверхні моделі вибраного очного яблука. У вікнах під номером 5, 6,9,10,13,14 відображають розраховані числові значення моментів сил м'яза відносно осей декартової системи координат - OX , OY , OZ відповідно для точок M і M ' . Для другого очного яблука процедура розрахунку аналогічна. У вікнах 7, 8,11,12,15,16 відображають числові значення моментів сил м'яза відносно осей декартової системи координат. Зорова вісь другого ока 19 має вплив на побудову векторів сил тяги. Для цього встановлюють позначку у вікнах 17 та 18 і також обирають тип м'яза. Технічний результат способу полягає у скороченні часу на проведення досліджень, а відповідно перебування пацієнта під наркозом, точно відображує окорухові структури очного яблука людини. Спосіб розрахунку результуючого моменту сили тяги всього комплексу м'язів на поверхні моделі очного яблука людини може використовуватись в офтальмології для підвищення ефективності хірургічних операцій. ФОРМУЛА КОРИСНОЇ МОДЕЛІ 40 Спосіб розрахунку результуючого моменту сили тяги всього комплексу м'язів на поверхні моделі очного яблука людини, який полягає у тому, що визначають сферичні координати на моделі обох очних яблук, які являють собою сфери з визначеним радіусом у відповідності до виразів: x 180 ; arctg 1 z1 180 arctg x1 180 , при z 0; 1 z1 1 x 180 , при z1 0, x1 xO1; 360 arctg 1 z1 dpp xO1 ; 2 3 UA 122980 U 1 arctg y1 2 2 x1 z1 180 ; x 180 ; arctg 2 z2 180 arctg x 2 180 , при z 0; 2 z2 1 x 180 , при z2 0, x 2 xO2; 360 arctg 2 z2 dpp x O2 ; 2 arctg 2 5 y2 x 2 z2 2 2 180 ; де x 1 , y 1 , z 1 , x 2 , y 2 , z 2 - декартові координати правого та лівого ока відповідно; 1 , 1 , 2 , 2 - сферичні координати сфери правого та лівого ока відповідно; x O1 , x O2 - координати правого та лівого ока відповідно з урахуванням відстані між центром очних яблук dpp , який відрізняється тим, що враховано зорову вісь іншого ока та моменти сил його групи м'язів, визначають момент сили м'яза відносно осей декартової системи координат у відповідності до виразів: 10 Mxi1 Fzi1 yi1 Fy i1 zi1; Myi1 Fx i1 zi1 Fzi1 xi1; Mzi1 Fy i1 xi1 Fx i1 yi1; Mxi2 Fzi2 yi2 Fy i2 zi2; My Fx z Fz x ; i2 i2 i2 i2 i2 Mzi2 Fy i2 xi2 Fx i2 yi2; де: Fx i1 , Fy i1 , Fz i1 , Fx i2 , Fy i2 , Fz i2 - проекції вектору сили тяги, що діє в i-й точці на осях OX , OY та OZ відповідно до кожного з очних яблук; Mx i1 , My i1 , Mz i1 , Mxi2 , Myi2 , Mzi2 - моменти векторів сил тяги відносно відповідних осей після обертання. 4 UA 122980 U Комп’ютерна верстка О. Гергіль Міністерство економічного розвитку і торгівлі України, вул. М. Грушевського, 12/2, м. Київ, 01008, Україна ДП “Український інститут інтелектуальної власності”, вул. Глазунова, 1, м. Київ – 42, 01601 5
ДивитисяДодаткова інформація
МПК / Мітки
МПК: G09B 23/28, A61B 3/00
Мітки: людини, комплексу, моменту, розрахунку, очного, тяги, результуючого, поверхні, яблука, сили, м'язів, спосіб, всього
Код посилання
<a href="https://ua.patents.su/7-122980-sposib-rozrakhunku-rezultuyuchogo-momentu-sili-tyagi-vsogo-kompleksu-myaziv-na-poverkhni-ochnogo-yabluka-lyudini.html" target="_blank" rel="follow" title="База патентів України">Спосіб розрахунку результуючого моменту сили тяги всього комплексу м’язів на поверхні очного яблука людини</a>











