Спосіб градуювання датчиків температури

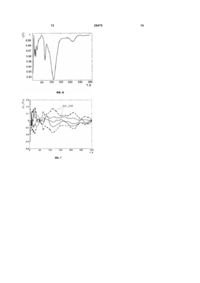
Спосіб градуювання датчиків температури, який полягає у визначенні індивідуальної градуювальної характеристики шляхом вимірювання величини електричного вихідного сигналу градуйованого датчика в не менше ніж двох N температурних точках Ti , де i = 1K N , діапазону робочих температур датчика, перша з яких T1 відповідає максимуму середньоквадратичного відхилення індивідуальних градуювальних характеристик датчиків даного типу від усередненої градуювальної характеристики для датчиків даного типу A 0 (T ) , з наступним розрахунком індивідуальної градуювальної характеристики A N (T ) у всьому 2 (13) 1 3 29475 Відомо, що технологічні особливості виготовлення деяких типів датчиків температури дозволяють їх виробництво з високою взаємозамінністю. При масовому виробництві датчиків це дає змогу використання замість індивідуальної ГХ конкретного термометра усередненої для даного типу датчиків характеристики A 0 (T ) : n = A 0 (T ) å f (T) k (1) = 1 k n де fk (T ) - індивідуальна ГХ k -го датчика з вибірки об'ємом n . Недоліками використання усередненої ГХ замість індивідуальних є велика похибка та необхідність відбраківки суттєвої кількості датчиків. Наприклад, за даними [1], для кремнієвих термодіодів серії DT-400 виробництва фірми Lake Shore Cryotronics, Inc. (США) економічно доцільна точність відповідності ГХ датчиків усередненій становить ±0,25К в діапазоні 2...100К, ±0,5К в діапазоні 100...305К та ±1К в діапазоні 305...475К. Більш точне вираження ГХ потребує відбраківки невиправдано великої кількості датчиків. Відомий спосіб градуювання з використанням усередненої ГХ, який передбачає вимірювання індивідуальної характеристики градуйованого термометра в двох температурних точках - аналог [1]. Даний спосіб названий ((програмним градуюванням» (далі, якщо немає окремих уточнень, слово «програмне» опускається). Оцінку індивідуальної ГХ градуйованого термометра A (T ) розраховують з виразу: A (T ) = m × A0 (T ) + [f (T2 ) - m × A 0 (T1 )] (2) де T1, T2 -температури, при яких проведено вимірювання індивідуальних ГХ f (T1 ) й f (T2 ) , відповідно; (f (T2 ) - f (T1)) - параметр нахилу. m= (A 0 (T2 ) - A 0 (T1)) Даний спосіб дозволяє скорегувати нахил і зміщення усередненої ГХ по відношенню до індивідуальної ГХ градуйованого термометра, тобто реалізує процедуру лінійної корекції по двом точкам шкали вимірювального приладу. На лінійній ділянці градуювальної характеристики даний спосіб дозволяє зменшити похибку визначення ГХ більш ніж в 3-рази, але при нелінійній - похибка значна. Відомий спосіб автоматичної компенсації розкиду датчиків різних фізичних величин [2] аналог, який також може бути використаний при градуюванні датчиків температури. Спосіб передбачає вимірювання вихідної величини градуйованого датчика в двох відомих температурних точках робочого діапазону T1 і T2 та розрахунок виміряного значення температури з допомогою виразу (вираз приводимо в позначеннях даного опису): T = [f (T) - (f ( 1 )+ Df (T1))] T (T2 - T1) +T [(f (T2 ) + Df (T2 )) - f (T1 )] 1 (3) 4 де f (T1) , f (T2 ) - значення вихідного сигналу, що відповідають усередненій ГХ при значеннях температури T1 і T2 , відповідно; f (T1)¢, f( T2) ¢ значення вихідного сигналу датчика в температурних точках T1 і T2 , відповідно; f (T ) - значення вихідного сигналу датчика при вимірюваній температурі T ; ( Df (T ) = f ( )- f T ¢); T 1 1 1 Df (T2 ) = f ( 2 ) - (f (T2 ) + Df (T1)) . T ¢ Даний спосіб дозволяє скоректувати розбіжності індивідуальних ГХ датчиків, що фактично вирішує задачу градуювання. Але даний спосіб також малоефективний для датчиків температури зі значною нелінійністю ГХ. Для нелінійних ГХ запропоновано використовувати спеціальні пристрої, що ускладнює апаратну частину системи градуювання. Відомий спосіб градуювання датчиків температури [3], обраний нами за прототип, який передбачає вимірювання електричної за природою величини на виході градуйованого датчика в точках, які відповідають максимумам залишкового середньоквадратичного відхилення (СКВ), і розрахунок оцінки індивідуальної ГХ з використанням функцій девіації, які характеризують розкид індивідуальних ГХ відносно усередненої для даного типу датчиків. Вихідними даними для проведення градуювання являється вибірка об'ємом п раніше отриманих в результаті повного градуювання індивідуальних ГХ датчиків одного типу з градуйованим. З допомогою (1) розраховують усереднену ГХ. Оцінка середньоквадратичного відхилення (СКВ) температурних відхилень індивідуальних ГХ вибірки від усередненої становить: E0 (T ) = 1 n -1 é fk (T ) - A 0 (T ) ù ú 0 (T ) / ¶T û k =1 n å êë ¶A 2 (4) СКВ (4) досягає максимуму при температурі Ti . Перший крок градуювання проводять при температурі Ti . Функцію девіації при кількості вимірювальних точок допомогою виразу: N 1 = визначають з n D1(T ) = å [(f (T) - A (T ))× S(f (T ) - A (T ))] k 0 k 1 0 1 k =1 n å [(f (T ) - A (T )) × S(f (T ) - A (T ))] k 1 0 1 k 1 0 (5) 1 k =1 ì +1 x ³ 0 - функція знаку. де S(x ) = í î- 1 x á 0 Розраховані ГХ першого ступеня для вихідної вибірки знаходять з виразу: A k,1(T ) = A 0 (T ) + [fk (T1) - A 0 (T1)]× D1(T ) (6) 5 29475 Функція девіації D1(T ) введена таким чином, що A k,1(T1) = fk (T1) . В інших температурних точках розраховані ГХ A k,1(T ) відрізняються від дійсних fk (T ) на величину, яка залежить від властивостей даного типу датчиків. Цю величину оцінюють з допомогою СКВ E1(T ) з виразу (4), де замість A 0 (T ) підставляють E1(T ) залежність A k,1(T ) . набуває Температурна максимального значення в температурній точці T2 . Для T2 проводять розрахунок функції девіації D2 (T ) і.ГХ другого ступеня наближення A k,2 (T ) . В загальному випадку на i -му кроці обробки вихідної вибірки СКВ похибки наближення індивідуальних ГХ розраховують з виразу: 1 n - i -1 Ei-1(T ) = é fk (T ) - Ak , i (T ) ù ú ê û ë ¶A k , 0 (T ) ¶T ú k =1 ê n å Для максимуму Ei-1(T ) розраховують функцію девіації n Di (T ) = å [(f (T) - A k k,i k =1 n å [(f (T ) - A k i k,i 2 (7) в точці Ti (T )) × S(fk (Ti ) - A k,i (Ti ))] (Ti ))× S(fk (Ti ) - Ak,i (Ti ))] (8) k =1 з допомогою якої розраховують ГХ і - го ступеня наближення A k,i (T ) = A k,i -1(T ) + fk (Ti ) - A k,i-1(Ti ) × Di (T ) (9) Описана ітеративна процедура обробки вихідної вибірки повторюють N раз до моменту, коли максимум СКВ EN (T ) стане меншим ніж допустиме значення. Отримані функції Di (T ) , де = 1K N , i використовують при градуюванні датчиків, ГХ яких не використовувались при розрахунках. Розраховану ГХ градуйованого датчика N-гo ступеня отримують з виразу: [ AN (T ) = A0 (T ) + ] N å [(f (T ) - A i ( )) × Di T ]) ( i-1 Ti (10) i=1 За даними [3], градуювання з допомогою способу-прототипу дозволяє зменшити кількість вимірювальних точок для отримання індивідуальної ГХ з необхідною точністю. В якості міри точності такого градуювання запропоновано використовувати максимальне значення СКВ EN (T ) . Спосіб дозволяє проводити градуювання датчиків як з лінійними, так і нелінійними ГХ. Недоліками способу є низька точність, яку характеризує значна величина EN (T ) , та неможливість оцінки дійсної похибки отриманої ГХ A N (T ) . Величина EN (T ) являється статистичним показником і характеризує точність визначення ГХ значної кількості датчиків. На практиці ж необхідно 6 оцінити точність градуювання даного конкретного датчика, що розглянутий спосіб не дозволяє. Задачею даної корисної моделі є розробка такого способу градуювання датчиків температури, який дозволить підвищити точність оцінки ГХ при тій самій або меншій кількості вимірювальних точок. Поставлена задача вирішена тим, що в способі градуювання датчиків температури, який полягає у визначенні індивідуальної градуювальної характеристики шляхом вимірювання величини електричного вихідного сигналу градуйованого датчика в не менше ніж двох N температурних точках Ti , де i = 1K N , діапазону робочих температур датчика, перша з яких T1 відповідає максимуму середньоквадратичного відхилення індивідуальних градуювальних характеристик датчиків даного типу від усередненої градуювальної характеристики для датчиків даного типу A 0 (T ) , з наступним розрахунком індивідуальної градуювальної характеристики A N (T ) у всьому діапазоні робочих температур на основі A 0 (T ) та функцій девіації, які характеризують розкид індивідуальних градуювальних характеристик датчиків даного типу, друге та наступні вимірювання вихідного електричного сигналу датчиків проводять в температурних точках Ti , де i = 2 K N , які відповідають мінімумам коефіцієнтів множинної кореляції між значеннями відхилень індивідуальних ГХ від усередненої у цих точках та значеннями відхилень індивідуальних ГХ від усередненої в довільних точках робочого температурного діапазону датчиків. В якості функцій девіації використовують коефіцієнти лінійної множинної регресії qi (T ) значень відхилень індивідуальних ГХ датчиків від усередненої в довільних температурних точках по значенням відхилень індивідуальних ГХ датчиків від усередненої в температурних точках, в яких проводять вимірювання. Індивідуальну градуювальну характеристику градуйованого датчика розраховують з виразу: AN (T ) = A0 (T ) + N å [(f (T ) - A (T ))× q (T )] i i=1 0 i i (11) де f (Ti ) - виміряне значення вихідного електричного сигналу датчика в температурній точці Ti . Вихідними даними для проведення градуювання являється вибірка об'ємом n раніше отриманих в результаті повного градуювання дійсних індивідуальних ГХ датчиків температури даного типу. Як і в способі-прототипі, перша температурна точка T1 , в якій проводиться вимірювання вихідного сигналу датчика, відповідає максимальному значенню середньоквадратичного відхилення E0 (T ) , розрахованого з (4). 7 29475 Для встановлення решти N - 1 температурних точок Ti , де i = 2 K N , в яких необхідно проводити вимірювання проводиться кореляційний аналіз ГХ, які входять у вибірку. Матриця даних для вибірки об'ємом n при кількості вимірювальних точок N має вигляд: é Df1(T ) Df1(T1) K Df1(TN )ù ú ê Df (T ) Df2 (T1) K Df2 (TN )ú X=ê 2 (12) ê K K K K ú ú ê ê Dfn (T ) Dfn (T1) K Dfn (TN )ú û ë де Dfk (T ) = fk (T ) - A 0 (T ) температурна залежність відхилення k-ї дійсної індивідуальної ГХ від усередненої; fk (T ), k = 1K n - дійсна індивідуальна ГХ k-го датчика, отримана в результаті повного градуювання. Матриці даних X відповідає кореляційна матриця: ér00 r01 K r0N ù ú ê r r11 K r1N ú R = ê 10 (13) êK K K K ú ú ê êrN0 rN1 K rNN ú û ë n å (Df (T )× Df (T )) k rij = де k 1 = n å Df k k 1 = 2 i k парні (Ti ) × å Dfk2 (Tj ) коефіцієнти кореляції, i, j = 1K N . Нульові значення індексів i та j відповідають першому стовпчику матриці X , елементи якого являються функціями температури. Оцінкою стохастичного функціонального зв'язку Dfk (T ) з Dfk (Ti ) , i = 1K N є коефіцієнт множинної кореляції, який розраховують з виразу: (14) де det (R) - визначник матриці R ; R00 (T ) - алгебраїчне доповнення елементу r00 кореляційної матриці R . В точці T = T1, rN (T1) = 1 , що відповідає повній функціональній визначеності. При віддаленні температури T від точки вимірювання T1 , rN (T ) набуває значень в діапазоні від 1 до 0, причому чим ближче до нуля, тим слабший функціональний зв'язок. Для більшості практичних випадків значимість коефіцієнта множинної кореляції може бути перевірена з допомогою t - критерію Ст'юдента із співвідношення [4]: rN (T ) × n - N - 1 ³ t1-p (n - N - 1) (15) 1 - rN2 (T ) ( ) Ст'юдента для n - N - 1 ступенів свободи та довірчої вірогідності Р. Якщо нерівність (15) не виконується для певного діапазону температур, rN приймають незначимим, і кількість вимірювальних точок N збільшують на 1. В якості наступної вимірювальної точки приймають температуру T2 , при якій абсолютна величина r1 , набуває мінімального значення. Для оновленої матриці даних X, яка включає стовпчик [Df (T ), Df (T )K Df (T )]¢ , 1 2 2 2 n 2 розраховують rN і перевіряють його значимість. Описану процедуру повторюють поки коефіцієнт множинної кореляції не стане значимим в усьому робочому діапазоні даного типу датчиків. Наступною операцією обробки вихідних даних є регресійний аналіз, метою якого є побудова регресійної моделі індивідуальних ГХ. Модель множинної лінійної регресії Dfk по Dfk (Ti ) має вигляд AN,k (T ) = A 0 (T ) + N å [(f (T ) - A (T ))× q (T ]) k i 0 i (16) i i= 1 E0 (T ) Q0i × - частинні коефіцієнти E0i Q00 лінійної регресії; Qij - алгебраїчне доповнення елемента rij матриці R ; k 1 = det (R ) rN (T ) = 1 R 00 (T ) де t1-p (n - N - 1) - табличне значення критерію де qi (T ) = j n 8 E0 (T ) = n æ Dfk (T ) ö ÷ ç ç ¶A ¶T ÷ 0 ø 1è å 1 n -1 k= 2 - СКВ елементів 1-го стовпчика матриці даних X ; E0 i = 1 n -1 æ Dfk (Ti ) ö ÷ ç ç ¶A ¶T ÷ , 0 ø k =1 è n å 2 i = 1K N СКВ елементів і-го стовпчика матриці даних X . Частинні коефіцієнти регресії qi (T ) в даному випадку відіграють роль аналогічну до функцій девіації Di (T ) способу-прототипу. Модель (16) дозволяє оцінити ГХ, які входять до вибірки з СКВ температурної похибки, яке аналогічно до (7) можемо розрахувати з допомогою виразу: EN (T ) = 1 n -N -1 é fk (T ) - AN,k (T ) ù ê ú ¶A 0 (T ) ¶T û k =1 ë n å 2 (17) EN (T ) характеризує точність наближення індивідуальних ГХ. За цим параметром модель множинної лінійної регресії (16) є оптимальною, тобто гарантує мінімальне значення EN для даних вимірювальних точок [T1 , T2 K TN ] . Це свідчить про вищу точність запропонованого способу в порівнянні зі способом-прототипом. Крім того, якщо регресійні залишки Dfk (T ) = A N, k (T ) - fk (T ) (18) 9 29475 апроксимуються нормальним розподілом, є можливість оцінки абсолютної похибки наближення ГХ градуйованого датчика. Довірчий інтервал для граничної похибки регресійної моделі при довірчій імовірності Р визначають з виразу [4]: ( DTAN, k (T ) á t 1-P (n - N - 1) × EN (T ) × 1 + y T × X T × X 2 t 1-P (n - N - 1) де квантиль ) -1 ×y (19) розподілу 2 Ст'юдента для довірчої ймовірності Р та кількості ступенів свободи n - N - 1 ; y = (1 Df (T1) K Df (TN ))T - вектор даних для градуйованого датчика. Можливість розрахунку граничної похибки градуювання для моделі у вигляді (16) являється також перевагою запропонованої корисної моделі в порівнянні з розглянутими аналогами та прототипом. Приклади Для експериментальної перевірки запропонованої корисної моделі проводилося градуювання трьох кремнієвих діодних датчиків температури, розроблених в ІФН НАН України. Вихідним сигналом діодного датчика температури являється спад напруги при пропусканні через нього постійного прямого струму, а дійсна індивідуальна ГХ являє собою залежність спаду напруги на термодіоді від температури. На Фіг.1 зображено типову ГХ кремнієвих термодіодів в робочому діапазоні 4,2...300К. Вихідними даними для проведення градуювання являється вибірка дійсних ГХ об'ємом n=39, які отримані в результаті повного градуювання однотипних датчиків з робочим діапазоном 4,2...300К. На Фіг.2 зображено температурні залежності відхилень індивідуальних ГХ від усередненої, виражених в температурному f (T ) - A 0 (T ) . На Фіг.3 (крива 1) еквіваленті DTk = k ¶A 0 (T ) ¶T показана температурна залежність вибіркового СКВ E0 (T ) , розрахована з допомогою виразу (4). Максимального значення E0 (T ) набуває при температурі Т1=300К. Саме цю температурну точку приймаємо в якості першої точки для проведення вимірювання спаду напруги. На Фіг.4 зображено температурну залежність множинного коефіцієнта кореляції r1 , розрахованого з допомогою виразу (14), для однієї вимірювальної точки Т1=300К. Проводимо перевірку значимості коефіцієнта кореляції з допомогою нерівності (15). Табличне значення критерію Ст'юдента для кількості ступенів свободи 37 та довірчої вірогідності 0,95 становить 1,69 [4]. Значення rN (T ) × n - N - 1 при N = 1 перевищує дану 1 - rN2 (T ) величину не у всьому досліджуваному діапазоні. Коефіцієнт кореляції r1(T ) становить 0 в температурних точках 10 і 50К. На Фіг.5 показано ( ) 10 температурну залежність множинного коефіцієнта кореляції для двох вимірювальних температурних точок (50К і 300К), а на Фіг.6 - для трьох (10К, 50К та 300К). Як бачимо, при вимірюванні вихідного сигналу датчика в трьох температурних точках коефіцієнт множинної кореляції r3 (T ) не менший за 0,9 у всьому робочому діапазоні датчиків, що свідчить про наявність сильного стохастичного функціонального зв'язку значень ГХ в довільних температурних точках робочого діапазону датчика зі значеннями ГХ в названих температурних точках. Для трьох температурних точок побудована модель множинної лінійної регресії виду (15). Температурна залежність залишкового СКВ E3 (T ) (16) для побудованої моделі, а також для способупрототипу зображено на Фіг.3 (крива 2 та 3, відповідно). З Фіг.3 видно, що практично у всьому дослідженому температурному діапазоні залишкове СКВ для моделі (16) має менше значення, ніж для способу-прототипу. Це свідчить про вищу точність розрахунку індивідуальних ГХ з допомогою запропонованого способу в порівнянні зі способом-прототипом. Запропонований спосіб був використаний для градуювання 3-х датчиків, ГХ яких не увійшли у вихідну вибірку. На Фіг.7 показано температурну похибку моделі відносно дійсних ГХ fk (T ) , встановлених в процесі повного градуювання, яка розрахована з виразу: A N, k (T ) - fk (T ) DTA N, k (T ) = (20) ¶A 0 (T ) ¶T ( Максимальне ) значення DTA N, k (T ) для градуйованих датчиків становить 0,056К; 0,025К та 0,036К. Аналогічні значення при градуюванні з допомогою способу-прототипу становлять 0,065К; 0,048К та 0,044К, відповідно. Отже, новий спосіб дозволив підвищити точність градуювання при тій самій кількості вимірювальних точок. На Фіг.7 пунктиром показано довірчий інтервал для похибки градуювання з допомогою запропонованого способу DTA N , k (T ) , розрахований з виразу (19). Як бачимо, похибка не перевищує теоретично розрахованого граничного значення. Отже, запропонований спосіб градуювання дозволяє провести оцінку зверху граничного значення похибки визначення ГХ. Таким чином розроблений спосіб градуювання дозволив підвищити точність програмного градуювання в порівнянні зі способом-прототипом, для тієї самої кількості точок, в яких проводяться вимірювання. Джерела інформації: 1. Dodrill B. C., Krause J. K., Swinehart P. R., Wang V. Performance Characteristics of Silicon Diode Cryogenic Temperature Sensors // Applications of Cryogenic Technology. - 1991. - 10. - P.85-107. 2. Пат. 4481596 США, МКИ G01К7/10. Method of and apparatus for automatically compensating for variations in output response characteristics of sensors and the like: Пат. 4481596 США, МКИ 11 G01К7/10 / David Townzen (США); Kaye Instruments Inc. - №316999; Заявл. 02.11.81; Опубл. 06.11.84; МКИ 364/571. -8с. 3. Nara К., Kato H., Okaji M. - Derivation of optimized calibration procedures for practical thermometers. // Cryogenics. -1995. -35, N 5. -P.291295 - прототип. 4. Айвазян С. А., Енюков И. С, Мешалкин Л. Д. Прикладная статистика: Исследование зависимостей: / Справочное издание - М.: Финансы и статистика, 1985. - 487с. 29475 12 13 29475 14