Нейронна мережа
Номер патенту: 115589
Опубліковано: 25.04.2017
Автори: Турти Марина Валентинівна, Кутковецький Валентин Якович
Формула / Реферат
1. Нейронна мережа, яка має сенсорний шар з кількістю нейронів ![]() , кожний з яких має один вхід з ваговим коефіцієнтом 1 та
, кожний з яких має один вхід з ваговим коефіцієнтом 1 та ![]() виходів з порядковими номерами
виходів з порядковими номерами ![]() , має увімкнені до відповідних входів нейронів сенсорного шару змінні
, має увімкнені до відповідних входів нейронів сенсорного шару змінні ![]() вхідного вектора
вхідного вектора ![]() , де
, де ![]() - порядковий номер змінних
- порядковий номер змінних ![]() вхідного вектора
вхідного вектора ![]() , має асоціативний шар з кількістю нейронів
, має асоціативний шар з кількістю нейронів ![]() , кожний з яких має
, кожний з яких має ![]() входів з ваговими коефіцієнтами входів, рівними значенням елементів відповідного еталонного вектора
входів з ваговими коефіцієнтами входів, рівними значенням елементів відповідного еталонного вектора ![]() , де
, де ![]() - порядковий номер нейрона асоціативного шару та його еталонного вектора
- порядковий номер нейрона асоціативного шару та його еталонного вектора ![]() , та має один вихід, призначений для видачі скалярного добутку двох векторів у вигляді значення
, та має один вихід, призначений для видачі скалярного добутку двох векторів у вигляді значення ![]() , має реагуючий шар з одним нейроном, який має
, має реагуючий шар з одним нейроном, який має ![]() входів з ваговим коефіцієнтом 1, до яких увімкнені відповідні виходи
входів з ваговим коефіцієнтом 1, до яких увімкнені відповідні виходи ![]() нейронів асоціативного шару, яка відрізняється тим, що нейрон реагуючого шару має один вихід, призначений для виведення порядкового номеру
нейронів асоціативного шару, яка відрізняється тим, що нейрон реагуючого шару має один вихід, призначений для виведення порядкового номеру ![]() еталонного вектора
еталонного вектора ![]() , який має найбільший скалярний добуток з вхідним вектором
, який має найбільший скалярний добуток з вхідним вектором ![]() , згідно з активаційною функцією
, згідно з активаційною функцією
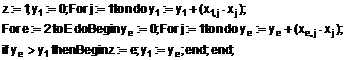
де ![]() - вихід нейрона реагуючого шару та нейронної мережі у вигляді порядкового номера
- вихід нейрона реагуючого шару та нейронної мережі у вигляді порядкового номера ![]() еталонного вектора
еталонного вектора ![]() , який має найбільший скалярний добуток з вхідним вектором
, який має найбільший скалярний добуток з вхідним вектором ![]() ;
;
![]() - елементи з j-м порядковим номером векторів
- елементи з j-м порядковим номером векторів ![]() та
та ![]() ;
;
![]() - скалярний добуток векторів
- скалярний добуток векторів ![]() та
та ![]() ;
;
![]() - порядковий номер еталонного вектора
- порядковий номер еталонного вектора ![]() ;
;
![]() - порядковий номер елементів
- порядковий номер елементів ![]() та
та ![]() векторів
векторів ![]() та
та ![]() .
.
2. Нейронна мережа за п. 1, яка відрізняється тим, що вихід нейрона реагуючого шару призначений для виведення порядкового номеру ![]() еталонного вектора
еталонного вектора ![]() , що має найменший скалярний добуток з вхідним вектором
, що має найменший скалярний добуток з вхідним вектором ![]() , згідно з активаційною функцією
, згідно з активаційною функцією
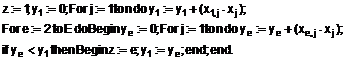
3. Нейронна мережа за п. 1, яка відрізняється тим, що активаційна функція нейрона реагуючого шару має вектор кодованих повідомлень ![]() , а вихід нейрона реагуючого шару призначений для видачі кодованого повідомлення
, а вихід нейрона реагуючого шару призначений для видачі кодованого повідомлення ![]() , яке відповідає порядковому номеру
, яке відповідає порядковому номеру ![]() еталонного вектора
еталонного вектора ![]() з найбільшим скалярним добутком з вхідним вектором
з найбільшим скалярним добутком з вхідним вектором ![]() , згідно з активаційною функцією
, згідно з активаційною функцією
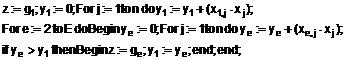
де ![]() - вектор кодованих повідомлень;
- вектор кодованих повідомлень;
![]() - кодоване повідомлення на виході нейронної мережі.
- кодоване повідомлення на виході нейронної мережі.
4. Нейронна мережа за п. 2, яка відрізняється тим, що активаційна функція нейрона реагуючого шару має вектор кодованих повідомлень ![]() , а вихід нейрона реагуючого шару призначений для видачі кодованого повідомлення
, а вихід нейрона реагуючого шару призначений для видачі кодованого повідомлення ![]() , яке відповідає порядковому номеру
, яке відповідає порядковому номеру ![]() еталонного вектора
еталонного вектора ![]() з найменшим скалярним добутком з вхідним вектором
з найменшим скалярним добутком з вхідним вектором ![]() , згідно з активаційною функцією
, згідно з активаційною функцією
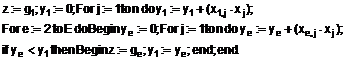
5. Нейронна мережа за пп. 1-4, яка відрізняється тим, що замість міри близькості ![]() використовується близькість по Хеммінгу для векторів з елементами «+1» та «-1»
використовується близькість по Хеммінгу для векторів з елементами «+1» та «-1»
![]()
або квадрат евклідової відстані (із зміною в активаційних функціях знаків нерівності на протилежні значення)
![]()
Текст
Реферат: UA 115589 U UA 115589 U 5 Корисна модель належить до штучних нейронних мереж (НМ), призначених для асоціативного розпізнавання образів. Асоціативне розпізнавання образів застосовується в нейрокібернетиці і може бути використане в нейрокомп'ютерах та в штучних нейронних мережах при розв'язанні задач логічної обробки даних. Відома одношарова НМ Хопфілда, яка призначена для асоціативного розпізнавання образу, що описується вектором X ( x1 , x2 , , x j , , xn ) з елементами "±1", і для циклічних перерахунків змінних x j вхідного вектора X ( x1 , x2 , , x j , , xn ) , де порядковий номер змінних x j вхідного вектора X, j 1,2, , n у змінні y j відповідного асоціативного вектора виходу Y ( y1 , y 2 , , y j , , y n ) до отримання сталого стану вектора виходу Y, яка 10 має шар з кількістю нейронів n з пороговою функцією активації, кожний з яких має вихід, який з'єднаний з входами інших нейронів з визначеними ваговими коефіцієнтами [1, 2, 3]. Недоліками НМ Хопфілда є мала кількість еталонних сигналів, які запам'ятовуються у вагах входів нейронів та необхідність виконання ряду циклічних розрахунків для визначення на виході НМ найближчого еталонного сигналу X e ( xe ,1 , xe , 2 , , xe , j , , xe ,n ) , де e 1,2,, E 15 порядковий номер еталону; E 0,10,15n . Відома НМ Хеммінга, яка має сенсорний шар з кількістю нейронів n , кожний з яких має один вхід з ваговим коефіцієнтом 1 та E виходів з порядковими номерами e 1,2,, E , має увімкнені до відповідних входів нейронів сенсорного шару змінні 20 x j вхідного вектора X ( x1 , x2 , , x j , , xn ) , де j 1,2, , n - порядковий номер змінних x j , вхідного вектора X , має асоціативний шар з кількістю нейронів E , кожний з яких має n входів з ваговими коефіцієнтами входів, рівними значенням елементів відповідного еталонного вектора X e ( xe ,1 , xe , 2 , , xe, j , , xe ,n ) , де e 1,2,, E - порядковий номер нейрона асоціативного шару та його еталонного вектора X e ( xe ,1 , xe , 2 , , xe, j , , xe ,n ) , та має один вихід, призначений для видачі скалярного добутку двох векторів у вигляді значення ye j 1 xe, j x j , n 25 який увімкнений до відповідного е-го входу з ваговим коефіцієнтом 1 реагуючого шару у вигляді мережі MAXNET, яка має шар з E нейронів, кожний з яких має один вхід, один вихід та зворотні зв'язки, що призначені для підсилення власного виходу нейрона та зменшення виходів інших нейронів, і призначена для видачі на виході мережі MAXNET, що також є виходом нейронної мережі, вектора Z ( z1 , z 2 , , ze , , z E ) з нульовими елементами, серед яких дорівнює 1 30 елемент з найбільшим скалярним добутком вхідного вектора X та еталонного вектора X e [4]. Недоліками НМ Хеммінга є: - велика кількість виходів, яка для ряду систем управління вимагає наступного переведення їх у порядковий номер e виділеного еталонного вектора X e . Збільшена кількість нейронів 35 40 45 виходу збільшує вартість і ускладнює схему НМ; - обмеження значень елементів вхідного X та еталонного X e векторів величинами "+1" та "-1"; - відсутність можливості подачі цифрового кодованого повідомлення у відповідь на вхідний вектор X , яке дозволяє використовувати обмежену кількість дій у відповідь на більшу кількість розпізнаних еталонних векторів X e ; - циклічні перерахунки мережі MAXNET для виділення максимального виходу. Найбільш близьким до заявленої нейронної мережі за сукупністю суттєвих ознак є вибрана за прототип відома нейронна мережа "Миколаїв" [5]. НМ "Миколаїв" призначена для асоціативного розпізнавання образів, має сенсорний шар з кількістю нейронів n , кожний з яких має один вхід з ваговим коефіцієнтом 1 та E виходів з порядковими номерами e 1,2,, E , має увімкнені до відповідних входів нейронів сенсорного шару змінні x j , вхідного вектора X ( x1 , x2 , , x j , , xn ) , де номер змінних x j вхідного вектора j 1,2, , n - порядковий X , має асоціативний шар з кількістю нейронів E , кожний з 1 UA 115589 U яких має n входів з ваговими коефіцієнтами входів, рівними значенням елементів відповідного еталонного вектора X e ( xe ,1 , xe , 2 , , xe , j , , xe ,n ) , де e 1,2,, E - порядковий номер нейрона асоціативного шару та його еталонного вектора X e ( xe ,1 , xe , 2 , , xe , j , , xe ,n ) , та має один вихід, призначений для видачі скалярного добутку двох векторів у вигляді значення 5 n ye j 1 xe, j x j , має реагуючий шар з одним нейроном, який має E входів з ваговим коефіцієнтом 1, до яких увімкнені відповідні виходи y e нейронів асоціативного шару, яка відрізняється тим, що нейрон реагуючого шару має E виходів для виведення вихідного вектора Z ( z1 , z2 ,, ze ,, z E ) , кожний елемент z e якого призначений для виведення значення "0", якщо 10 відповідне значення елемента вектора ye Y ( y1 , y2 ,, ye , , y E ) менше максимального значення елементів вектора Y та призначений для виведення значення "1", якщо значення елемента y e вектора Y дорівнює максимальному значенню елементів вектора Y , згідно з активаційною функцією, що призначена для виконання операцій for e : 1to E do ze : 0; ZM : y1; for e : 2 to E do if ye ZM then ZM : ye ; for e : 1to E do if ye ZM then ze : 1. 15 Причинами, які перешкоджають одержанню очікуваного технічного результату у прототипі (зменшення вартості через зменшення кількості виходів реагуючого шару і відсутності перерахунку вихідних даних у порядковий номер виділеного еталонного вектора X e ; 20 збільшення функціональних можливостей внаслідок використання кодованих повідомлень у відповідь на вхідний вектор X , які дозволяють використовувати обмежену кількість дій у відповідь на більшу кількість E еталонних векторів), є прийняті функції реагуючого шару. Недоліками прийнятої за прототип НМ "Миколаїв" є: - збільшення витрат на обслуговування і налагодження НМ внаслідок необхідності перерахунку для деяких систем управління E виходів вектора Z на один вихід, призначений для виведення порядкового номеру виділеного еталонного вектора X e ; 25 30 35 - зменшення функціональних можливостей внаслідок відсутності кодованих повідомлень у відповідь на вхідний вектор X , які дозволяють використовувати обмежену кількість дій у відповідь на більшу кількість E еталонних векторів. Технічним результатом є: - зменшення витрат на обслуговування і налагодження НМ внаслідок відсутності перерахунку для деяких систем управління E виходів вектора Z на один вихід, призначений для виведення порядкового номеру виділеного еталонного вектора X e ; - збільшення функціональних можливостей внаслідок виведення на виході НМ кодованих повідомлень у відповідь на вхідний вектор X , які дозволяють використовувати обмежену кількість дій у відповідь на більшу кількість E еталонних векторів. Загальні суттєві ознаки запропонованої НМ, які співпадають з суттєвими ознаками прототипу, полягають у тому, що нейронна мережа, яка має сенсорний шар з кількістю нейронів n , кожний з яких має один вхід з ваговим коефіцієнтом 1 та E виходів з порядковими номерами e 1,2,, E , має увімкнені до відповідних входів нейронів сенсорного шару змінні x j вхідного вектора x X ( x1 , x2 , , x j , , xn ) , де j 1,2, , n - порядковий номер змінних j вхідного вектора X , має асоціативний шар з кількістю нейронів E , кожний з яких має n входів 40 з ваговими коефіцієнтами входів, рівними значенням елементів відповідного еталонного вектора X e ( xe ,1 , xe , 2 , , xe , j , , xe ,n ) , де e 1,2,, E - порядковий номер нейрона асоціативного шару та його еталонного вектора X e ( xe ,1 , xe , 2 , , xe , j , , xe ,n ) , та має один вихід, призначений для видачі скалярного добутку двох векторів у вигляді значення 2 UA 115589 U n ye j 1 xe, j x j , має реагуючий шар з одним нейроном, який має E входів з ваговим 5 коефіцієнтом 1, до яких увімкнені відповідні виходи y e нейронів асоціативного шару. Суттєві ознаки запропонованої НМ, що є достатніми у всіх випадках і характеризують запропоновану корисну модель на відміну від прототипу, полягають у тому, що нейрон реагуючого шару призначений для виведення порядкового номеру z e еталонного вектора X e , який має найбільший скалярний добуток з вхідним вектором X , згідно з активаційною функцією z : 1; y1 : 0; For j : 1to n do y1 : y1 ( x1, j x j ); For e : 2 to E do Begin ye : 0; For j : 1to n do ye : ye ( xe, j x j ); if ye y1 then Begin z : e; y1 : ye ; end ; end . 10 де z e - вихід нейрона реагуючого шару та нейронної мережі у вигляді порядкового номера e еталонного вектора X e , який має найбільший скалярний добуток з вхідним вектором X; xe , j , x j - елементи з j-м порядковим номером векторів X e та X ; ye - скалярний добуток векторів X e та X; e 1,2,, E - порядковий номер еталонного вектора X e ; j 1,2, , n - порядковий номер елементів x j та xej векторів X та X e . 15 Передбачувана НМ показана схемою, на якій наведена схема пропонованої нейронної мережі. На кресленні використані наступні позначення: - X ( x1 , x2 , , x j , , xn ) - вхідний вектор, який вводиться у сенсорний шар, що 20 25 складається з n нейронів N x1 , N x 2 , , N xj , , N xn ; - 1 - вагові коефіцієнти входів нейронів; - N x1 , N x 2 , , N xj , , N xn - нейрони сенсорного шару кількістю n , кожний з яких має один вхід з ваговим коефіцієнтом "1" та E виходів. З метою спрощення малюнка на кресленні показані не всі виходи нейронів сенсорного шару. У повному комплекті вони наведені лише для нейрона N x1 . У дійсності кожний з нейронів сенсорного шару N x1 , N x 2 , , N xj , , N xn має E виходів, з'єднаних з відповідними входами E нейронів асоціативного шару N y1 , N y 2 , , N ye , , N yE . 30 - N y1 , N y 2 , , N ye , , N yE - нейрони асоціативного шару. Вагові коефіцієнти n входів кожного нейрона асоціативного шару дорівнюють відповідним елементам еталонного вектора X e ( xe ,1 , xe , 2 , , xe, j , , xe ,n ) , де e 1,2,, E - порядковий номер еталонного вектора X e . Вихід кожного з E добутку двох векторів нейронів асоціативного шару призначений для отримання скалярного X та X e у вигляді ye j 1 xe, j x j . E виходів нейронів асоціативного n шару призначені для передачі сигналу у вигляді вектора Y ( y1 , y2 , , ye , , y E ) і з'єднані з входами з ваговими коефіцієнтами "1" реагуючого шару у вигляді нейрона N z . З метою спрощення малюнка на кресленні показані не всі входи нейронів асоціативного шару. У повному комплекті вони наведені лише для нейрона N y1 . У дійсності кожний з нейронів асоціативного E 35 шару N y1 , N y 2 , , N ye , , N yE має n входів, з'єднаних з відповідними n виходами нейронів сенсорного шару N x1 , N x 2 , , N xj , , N xn . 3 UA 115589 U Y ( y1 , y2 , , ye , , y E ) , e 1,2, , E вектор виходу асоціативного шару з ye j 1 xe, j x j , де xe, j - j-ий елемент е-го еталонного вектора X e ; x j - j-й n елементами елемент вхідного вектора X ; - e 1,2,, E - порядковий номер еталонних векторів X e ; 5 N z - нейрон реагуючого шару, який має E входів з ваговими коефіцієнтами "1", на кожний з яких увімкнено відповідне значення y e , та один вихід, призначений для виведення значення z e (порядкового номера e еталонного вектора X e з найбільшим скалярним добутком з вхідним вектором X ). Нейрон N z складається з блока активаційної функції, що призначена для виконання операцій z : 1; y1 : 0; For j : 1to n do y1 : y1 ( x1, j x j ); For e : 2 to E do Begin ye : 0; For j : 1to n do ye : ye ( xe, j x j ); if ye y1 then Begin z : e; y1 : ye ; end ; end . - z e - вихід нейрона реагуючого шару N z , який також є виходом нейронної мережі. 10 НМ не потребує процесу навчання. Розглянемо загальний опис НМ, згідно з наведеним кресленням. До входів нейронів з ваговим коефіцієнтом "1" N x1 , N x 2 , , N xj , , N xn сенсорного шару 15 НМ (див. креслення) увімкнені елементи вхідного вектора X ( x1 , x2 , , x j , , xn ) . кожного з нейронів з'єднані N x1 , N x 2 , , N xj , , N xn з відповідним входом E виходів нейронів асоціативного шару N y1 , N y 2 , , N ye , , N yE . Вагові коефіцієнти n входів кожного нейрона асоціативного шару дорівнюють відповідним елементам еталонного вектора X e ( xe ,1 , xe , 2 , , xe, j , , xe ,n ) . E виходів нейронів 20 асоціативного шару призначені для передачі сигналу у вигляді вектора Y ( y1 , y2 ,, ye , , y E ) , e 1,2,, E , ye j 1 xe, j x j , і з'єднані з E входами з ваговими n коефіцієнтами "1" нейрона N z реагуючого шару. Нейрон N z реагуючого шару має один вихід для видачі вихідного сигналу НМ z : e , згідно з активаційною функцією, що призначена для виконання операцій z : 1; y1 : 0; For j : 1to n do y1 : y1 ( x1, j x j ); For e : 2 to E do Begin ye : 0; For j : 1to n do ye : ye ( xe, j x j ); 25 if ye y1 then Begin z : e; y1 : ye ; end ; end . Нейронна мережа працює наступним чином. При введенні у сенсорний шар вхідного вектора X ( x1 , x2 , , x j , , xn ) , для якого потрібно визначити номер найближчого еталонного вектора (з найбільшим значенням міри близькості), кожний е-й нейрон асоціативного шару має на виході значення скалярного добутку двох векторів у вигляді ye j 1 xe, j x j n 30 . Скалярний добуток двох векторів y e визначає міру близькості між двома векторами X e та X. Скалярний добуток двох векторів X e та X , хоча і визначає міру близькості між двома векторами, але разом з тим по числовому значенню відрізняється від близькості по Хеммінгу. Елементи отриманого вектора скалярних добутків Y ( y1 , y2 , , ye , , y E ) на виходах 35 E нейронів асоціативного шару увімкнені до відповідних E входів з ваговими коефіцієнтами "1" нейрона N z реагуючого шару, який має один вихід, призначений для виведення порядкового 4 UA 115589 U номеру z e еталонного вектора X e , який має найбільший скалярний добуток з вхідним вектором X , згідно з активаційною функцією z : 1; y1 : 0; For j : 1to n do y1 : y1 ( x1, j x j ); For e : 2 to E do Begin ye : 0; For j : 1to n do ye : ye ( xe, j x j ); 5 if ye y1 then Begin z : e; y1 : ye ; end ; end . У результаті на виході нейрона N z реагуючого шару, який також є виходом НМ, з'являється вихід z e , значення якого дорівнює порядковому номеру еталонного вектора X e , що є найближчим до вхідного вектора X , бо має з вектором X найбільше значення скалярного добутку. Описана нейронна мережа дозволяє: 1. Вивести на виході порядковий номер z e еталонного вектора X e , що має найменший 10 скалярний добуток з вхідним вектором X , якщо використати активаційну функцію z : 1; y1 :0; For j : 1to n do y1 : y1 ( x1, j x j ); For e : 2 to E do Begin ye : 0; For j : 1to n do ye : ye ( xe, j x j ); if ye y1 then Begin z : e; y1 : ye ; end ; end . 2. Вивести на виході НМ кодоване повідомлення z g e у відповідь на визначений порядковий номер e еталонного вектора X e з найбільшим скалярним добутком з вхідним вектором X , згідно з активаційною функцією z : g1 ; y1 : 0; For j : 1to n do y1 : y1 ( x1, j x j ); 15 For e : 2 to E do Begin ye : 0; For j : 1to n do ye : ye ( xe, j x j ); if ye y1 then Begin z : g e ; y1 : ye ; end ; end ; де G ( g1 , g 2 , , g e , , g E ) - вектор кодованих повідомлень; z g e - кодоване повідомлення на виході нейронної мережі. 3. Вивести на виході НМ кодоване повідомлення z g e у відповідь на визначений порядковий номер e еталонного вектора X e з найменшим скалярним добутком з вхідним 20 вектором X , згідно з активаційною функцією z : g1 ; y1 : 0; For j : 1to n do y1 : y1 ( x1, j x j ); For e : 2 to E do Begin ye : 0; For j : 1to n do ye : ye ( xe, j x j ); if ye y1 then Begin z : g e ; y1 : ye ; end ; end . 4. Використати замість міри близькості у вигляді скалярного добутку ye j 1 xe, j x j n близькість по Хеммінгу для векторів з елементами "+1" та "-1": ye : 0; For j : 1to n do if (((xe, j 0) and ( x j 0)) or ((xe, j 0) and ( x j 0))) then ye : ye 1; 25 або (зі зміною знаків нерівності на протилежні значення у наведених вище активаційних функціях) квадрат евклідової відстані ye : 0; For j : 1to n do ye : ye ( xij x j )2 . 30 Використання запропонованої нейронної мережі дозволяє при відсутності процесу навчання зменшити витрати на обслуговування і налагодження НМ внаслідок зменшення кількості виходів нейрона у реагуючому шарі, спрощення розрахунків і розширення функціональних можливостей. Джерела інформації: 1. Hopfield J.J. Neural Networks and Physical Systems with Emergent Collective Computational Abilities // Proc. of the National Academy of Science. - 1982. - 79. - P. 2554-2558. 5 UA 115589 U 5 2. Hopfield J.J. Neurons with Graded Response Have Collective Computational Properties Like Those of Two-State Neurons // Proc. of the National Academy of Science. - 1982. - 81. - P. 30883092. 3. Руденко О.Г., Бодянський С.В. Штучні нейронні мережі. - Харків: ТОВ "Компанія СМІТ", 2006. - 404 с. 4. Lippman P.P. An Introduction to Computing with Neural Nets // IEEE ASSP Magazine. - 1987. № 4. - P. 4-22. 5. Кутковецький В.Я., Турти М.В. Нейронна мережа "Миколаїв". Патент України на корисну модель G06N 3/00, № 104872, 25.02.2016, Бюл. № 4. - 4 с. 10 ФОРМУЛА КОРИСНОЇ МОДЕЛІ 15 1. Нейронна мережа, яка має сенсорний шар з кількістю нейронів n , кожний з яких має один вхід з ваговим коефіцієнтом 1 та E виходів з порядковими номерами e 12,,E , має увімкнені , до відповідних входів нейронів сенсорного шару змінні вхідного вектора xj X ( x1 , x2 , , x j , , xn ) , де j 1,2,, n - порядковий номер змінних x j вхідного вектора X, має асоціативний шар з кількістю нейронів E , кожний з яких має n входів з ваговими коефіцієнтами входів, рівними значенням елементів відповідного еталонного вектора X e ( xe ,1 , xe , 2 , , xe , j , , xe ,n ) , де e 1,2,, E - порядковий номер нейрона асоціативного 20 шару та його еталонного вектора Xe ( x e,1, x e,2 ,, x e, j ,, x e,n ) , та має один вихід, призначений для видачі скалярного добутку двох векторів у вигляді значення ye j 1 xe, j x j , має n реагуючий шар з одним нейроном, який має E входів з ваговим коефіцієнтом 1, до яких увімкнені відповідні виходи y e нейронів асоціативного шару, яка відрізняється тим, що нейрон 25 реагуючого шару має один вихід, призначений для виведення порядкового номеру z e еталонного вектора X e , який має найбільший скалярний добуток з вхідним вектором X , згідно з активаційною функцією z : 1 y1 : 0; For j : 1to n do y1 : y1 ( x1, j x j ); ; For e : 2 to E do Beginy e : 0; For j : 1to n do y e : y e ( x e, j x j ); if y e y1 thenBeginz : e; y1 : y e ; end; end; де z e - вихід нейрона реагуючого шару та нейронної мережі у вигляді порядкового номера e еталонного вектора X e , який має найбільший скалярний добуток з вхідним вектором 30 x e, j , x j - елементи з j-м порядковим номером векторів X e та y e - скалярний добуток векторів X e та X; X; X; e 1,2,, E - порядковий номер еталонного вектора X e ; j 1,2,, n - порядковий номер елементів 35 x j та x ej векторів X та X e . 2. Нейронна мережа за п. 1, яка відрізняється тим, що вихід нейрона реагуючого шару призначений для виведення порядкового номеру z e еталонного вектора X e , що має найменший скалярний добуток з вхідним вектором X , згідно з активаційною функцією z : 1; y1 : 0; For j : 1to n do y1 : y1 ( x1, j x j ); For e : 2 to E do Begin ye : 0; For j : 1to n do ye : ye ( xe, j x j ); if ye y1 then Begin z : e; y1 : ye ; end ; end . 3. Нейронна мережа за п. 1, яка відрізняється тим, що активаційна функція нейрона реагуючого шару має вектор кодованих повідомлень G (g1, g2,, ge ,, gE ) , а вихід нейрона 40 реагуючого шару призначений для видачі кодованого повідомлення z g e , яке відповідає порядковому номеру e еталонного вектора X e з найбільшим скалярним добутком з вхідним вектором X , згідно з активаційною функцією 6 UA 115589 U z : g1 ; y1 : 0; For j : 1to n do y1 : y1 ( x1, j x j ); For e : 2 to E do Begin ye : 0; For j : 1to n do ye : ye ( xe, j x j ); if ye y1 then Begin z : g e ; y1 : ye ; end ; end ; де G (g1, g2,, ge ,, gE ) - вектор кодованих повідомлень; z g e - кодоване повідомлення на виході нейронної мережі. 5 4. Нейронна мережа за п. 2, яка відрізняється тим, що активаційна функція нейрона реагуючого шару має вектор кодованих повідомлень G ( g1 , g 2 , , g e , , g E ) , а вихід нейрона реагуючого шару призначений для видачі кодованого повідомлення z g e , яке відповідає порядковому номеру e еталонного вектора X e з найменшим скалярним добутком з вхідним вектором X , згідно з активаційною функцією z : g1 ; y1 : 0; For j : 1to n do y1 : y1 ( x1, j x j ); For e : 2 to E do Begin ye : 0; For j : 1to n do ye : ye ( xe, j x j ); if ye y1 then Begin z : g e ; y1 : ye ; end ; end . 10 5. Нейронна мережа за пп. 1-4, яка відрізняється тим, що замість міри близькості ye j 1 xe, j x j використовується близькість по Хеммінгу для векторів з елементами «+1» та «n 1» ye : 0; For j : 1to n do if (((xe, j 0) and ( x j 0)) or ((xe, j 0) and ( x j 0))) then ye : ye 1; 15 або квадрат евклідової відстані (із зміною в активаційних функціях знаків нерівності на протилежні значення) y e : 0; For j : 1to n do y e : y e ( x ij x j )2 . Комп’ютерна верстка О. Рябко Державна служба інтелектуальної власності України, вул. Василя Липківського, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут інтелектуальної власності”, вул. Глазунова, 1, м. Київ – 42, 01601 7
ДивитисяДодаткова інформація
МПК / Мітки
МПК: G06N 3/00
Код посилання
<a href="https://ua.patents.su/9-115589-nejjronna-merezha.html" target="_blank" rel="follow" title="База патентів України">Нейронна мережа</a>
Попередній патент: Муфта двоступінчастого цементування обсадних колон
Наступний патент: Нейронна мережа
Випадковий патент: Вологопроникний волокнистий нетканий матеріал












