Спосіб пошарової побудови виробів на базі вихідної тріангуляційної 3d моделі

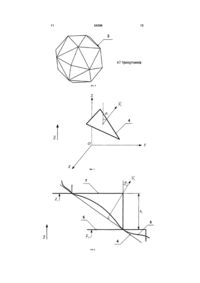
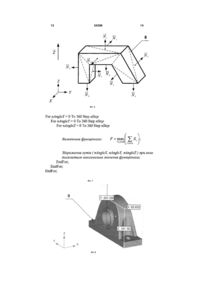
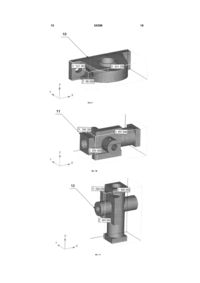
1. Спосіб пошарової побудови виробів на базі вихідної тріангуляційної 3D моделі, що включає установку виробу на робочій платформі, періодичне опускання столу на величину кроку побудови і наступне формування його шарів, який відрізняється тим, що для підвищення точності формоутворення і зменшення припуску під остаточну обробку, вироби орієнтуються на платформі таким чином, щоб сума площ трикутників тріангуляційної моделі, нормалі яких перпендикулярні або паралельні напрямку побудови виробу, була максимальною. 2. Спосіб за п. 1, який відрізняється тим, що перед етапом матеріалізації виробу на основі його тріангуляційної моделі максимізується функціонал по наступній формулі: Корисна модель відноситься до формоутворення, зокрема до пошарової побудови виробів на базі вихідної тріангуляційної 3D моделі, і може бути використане в машинобудуванні. Відомі способи побудови виробів пошаровими методами на установках швидкого прототипування, при якому вироби виготовляються шляхом послідовного нероз'ємного з'єднання елементарних шарів об'єму матеріалу, у якості якого можуть виступати полімер, кераміка, папір, метал і ін. [1-10]. Пошарові методи припускають прямий перехід від віртуальної 3D CAD моделі до матеріалізованого об'єкта. При даних способах 3D CAD модель виробу розсікається на серію послідовних дуже тонких шарів, звичайно 0,025-0,2мм товщиною, із деяким постійним дискретним кроком побудови. Товщина шаруючи обмежується технологічними можливостями застосовуваної установки швидкого прототипування. Точність і ефективність процесу пошарової побудови виробів залежить не тільки від висоти створюваних шарів матеріалу, але й від того, як вони розташовуються на робочій платформі установки швидкого прототипування. Від обраної орієнтації виробу в робочій камері буде залежати тривалість виготовлення, розрізняльна здатність і гладкість поверхні. Більш висока розрізняльна здатність кривих поверхонь досягається шляхом орієнтації їх у горизонтальній площині перпендикулярно лазерному променю. Похилі поверхні, що йдуть уздовж осі розщеплення, будуть мати «східчастий» вид. Було зроблено багато спроб [11-28] в області прийняття рішень у виборі оптимальної орієнтації виробів на робочій платформі використовуючи max Si , l j m l i n де Sі - площі трикутників, нормалі яких утворять із вектором побудови виробу кути 90° або 180°, тоб  то скалярний добуток векторів Ni, Z = 0 або -1 (13) 54398 (11) UA (19) відповідно; m - загальна кількість варіантів орієнтації виробу на робочій платформі; n - загальна кількість трикутників у тріангуляційній моделі виробу;  Ni - одиничний нормальний вектор і-го трикутника тріангуляційної моделі;  Z - одиничний вектор побудови виробу. U F 3 різні критерії точності, якості поверхні, об'єму підтримуючих структур і вартості. Недоліком цих способів являється те, що більшість із них [12, 13, 1719, 28] відносяться до процесів лазерної стереолітографії (SL). Дуже небагато робіт [11, 20, 22, 26, 27] присвячено процесам виборчого лазерного спікання (SLS), моделювання оплавленням (FDM) і ін. Найближчим до, що заявляється є спосіб побудови виробів пошаровими методами з попереднім оптимальним орієнтуванням їх на робочій платформі установки, описаний У [25]. При здійсненні цього способу, для побудови 3D моделі, авторами використовується модель шорсткості поверхні виробу, заснованої на техніці експериментальних статистичних розрахунків. Ця модель побудована раніше іншими авторами на базі експериментальних даних для товщини шаруючи = 0,006 дюйма й може бути використана для обчислення значення шорсткості поверхні тріангуляційної моделі у форматі STL-файлів. Це значення обчислюється для кожного вхідного в модель трикутника й потім обчислюється середнє значення шорсткості по всій поверхні моделі виробу. Далі вводиться спеціальна функція оптимальності, що розраховується для різних варіантів орієнтування моделі виробу. Мінімізація функції оптимальності здійснюється на основі методу довірчого інтервалу (Trust region method) із використанням комп'ютерного математичного пакета Matlab 6.5. Недоліком цього способу є складність застосування зазначеного методу для мінімізації функції оптимальності. Наступним недоліком являється те, що статистична модель шорсткості поверхні моделі побудована з використанням одного конкретного значення товщини шаруючи. При зміні кроку побудови модель буде не коректною, тому її застосування призведе до виникнення помилок. Зазначені недоліки в сукупності ведуть до збільшення технологічного часу виготовлення виробів за рахунок виникнення попередньої роботи з підготовчих операцій, пов'язаних з можливою побудовою нових статистичних моделей і ін., що знижує продуктивність процесу виготовлення в цілому. Завдання корисної моделі - розширення можливості застосування способу пошарової побудови виробів без обмежень на їхню складність, підвищення точності формоутворення окремих деталей і виробу в цілому, а також зменшення припуску під їх остаточну обробку. Технічний результат досягається тим, що при здійсненні способу пошарової побудови виробів на базі вихідної тріангуляційної 3D моделі, що включає установку виробу на робочій платформі, періодичне опускання столу на величину кроку побудови й наступне формування його шарів, з метою підвищення точності формоутворення й зменшення припуску під остаточну обробку, вироби орієнтують на платформі таким чином, щоб сума площ трикутників тріангуляційної моделі, нормалі яких перпендикулярні або паралельні напрямку побу 54398 4 дови виробу, була максимальної, при цьому даний функціонал максимізується по наступній формулі: F max Si l j m l i n (1) де Si- площі трикутників, нормалі яких утворять із вектором побудови виробу кути 90° або   180°, тобто скалярний добуток векторів Ni, Z =0 або -1 відповідно; m - загальна кількість варіантів орієнтації виробу на робочій платформі; n - загальна кількість трикутників у тріангуляційній моделі виробу;  Ni - одиничний нормальний вектор і-го трикутника тріангуляційної моделі;  Z - одиничний вектор побудови виробу. Відмітна ознака пропонованого рішення, що описує вибір оптимальної орієнтації виробу на платформі при його пошаровій побудові по формулі (1) представляється раніше невідомим технологічним прийомом. Наявність раніше невідомої ознаки дозволяє зробити висновок про відповідність пропонованого способу критерію "новизна". На Фіг.1-3 зображені 3 варіанти тріангуляційного представлення 3D моделі сфери, апроксимованої 1450, 450 і 67 трикутниками відповідно. На Фіг.4 зображений один з елементів (7-й трикутник) тріангуляційної 3D моделі сфери, апроксимованої 67 трикутниками, а також кут i , утво рений нормаллю i-го трикутника й вектором Z побудови виробу. На Фіг.5 представлена схема визначення кута між нормаллю трикутника й вектором побудови виробу при здійсненні пропонованого способу. На Фіг.6 зображена тріангуляційна модель виробу, що складається з 10 граней, а також нормалей до площин цих граней. На Фіг.7 представлений псевдокод знаходження кутів оптимальної орієнтації виробу на робочій платформі. На Фіг.8-13 представлені 3D моделі тестових виробів корпусу опори, корпусу й кронштейна відповідно для здійснення пропонованого способу пошарової побудови виробів. Розглянемо застосування пропонованого способу пошарової побудови виробів на основі тріангуляційної 3D моделі сфери. Як показано на Фіг.13, типові CAD програмні пакети (наприклад, 3D Systems, 1988) моделі твердотільних об'єктів, такі як сфера, представляють у вигляді набору трикутних граней. При цьому якість апроксимації моделі сфери прямо залежить від їхньої кількості. Іншими словами 3D модель виробу тріангулюють. На Фіг.1-3 зображена вихідна модель сфери, але що апроксимована різним числом трикутників: 1450 трикутниками - 1, 450 трикутниками - 2, 67 трикутниками - 3. На жаль, вищевказані CAD системи зберігають дані про тріангуляційний 3D моделі виробу в такій формі, що інформація про елементи (трикутниках) такої моделі зберігається незале 5 54398 жно друг від друга, без якої-небудь інформації про відношення одного трикутника щодо іншого. На Фіг.4 представлений один з елементів (i-й трикутник 4) тріангуляційної 3D моделі сфери, що апроксимований 67 трикутниками 3, а також кут i , утворений нормаллю і-го трикутника й векто ром Z побудови виробу. Споконвічно припускається, що напрямок побудови виробу збігається з позитивним напрямком осі OZ. На Фіг.5 представлена більш докладна схема розрахунку кута. Для наочності схема доповнена зображеннями східчастої побудови виробів. Приведена вихідна поверхня виробу 5, поверхня апроксимуючого трикутника  4 у розрізі, нормаль Ni ,. до його поверхні, кут i утворений нормаллю й вектором напрямку побудови виробу, дві січні площини 6 і 7 з координатами Zі-1 і Zі, відповідно. На Фіг.6 представлена тріангуляційна модель виробу 8, що складається з 10 граней. Кожна грань виробу розбита на певну кількість трикутників. При здійсненні пропонованого способу спочатку на підставі 3D CAD моделі виробу отримуємо тріангуляційну модель у форматі STL-файлу. Отриманий STL-файл використовується в якості вхідних даних для розробленої із цією метою програми. Далі вибирається спеціальне значення градуса крок, з яким модель виробу буде обертатися навколо осей координат. На підставі введеного значення кроку програма робить поворот моделі виробу по осях координат. На Фіг.7 представлений псевдокод визначення максимального значення функціонала (1). На кожному кроці система циклічно обробляє всі трикутники моделі й визначає по формулі (2) кут, утворений нормаллю поточного трикутника й вектором напрямку побудови виробу:   cos(Ni, Z) Nix Z x Niy Z y   Ni Z Niz Z z , (2)  де Ni - одиничний нормальний вектор і-го трикутника тріангуляційної моделі виробу; 6  Z - одиничний вектор побудови виробу. Якщо косинус даного кута дорівнює 0 або -1 (кут дорівнює 90° або 180° відповідно), то визначається площа цього трикутника. Далі провадиться підсумовування площ таких трикутників. По закінченні роботи програма визначає оптимальні кути орієнтування моделі виробу на робочій платформі, при яких функціонал (1) приймає найбільше значення. Таким чином, у результаті застосування пропонованого способу побудови виробів, отримуємо оптимальну їхню орієнтацію на робочій платформі, при якій досягається максимізація кількості апроксимуючих трикутників, що виключають можливість появи ефекту «ступінчастості» при виготовленні виробів, а виходить, підвищується точність формоутворення. Застосування даного способу зі способом адаптивного розділення на шари моделі виробу дозволяє досягати найкращих результатів при виготовленні з оптимальними показниками якості й часу. Приклади. Провадилося моделювання побудови тестових виробів, зображених на Фіг.8-13, для здійснення запропонованого способу. У першому випадку є модель корпусу опори 9, зображена на Фіг.8, з габаритними розмірами по осях координат 69,850 х 241,300 х 141,163мм відповідно. Орієнтація моделі виробу на платформі прямо залежить від рівня знань, а також від досвіду оператора установки пошарового виготовлення. Модель можна орієнтувати таким чином, щоб виріб займав якнайменше часу при виготовленні, але це зовсім не означає, що при цьому воно буде виготовлено з найкращими показниками точності. У результаті застосування запропонованого способу модель 9 буде орієнтована в такий спосіб 10 (Фіг.9), щоб досягти найкращої точності з наступними оптимальними кутами її повороту навколо осей координат. (табл. 1). Таблиця 1 Кут повороту по осі ОХ 0° Кут повороту по осі OY 90° У другому випадку є модель корпусу 11, зображена на Фіг.10, з габаритними розмірами по осях координат 497,840 х 368,300 х 254,000мм відповідно. У результаті застосування запропоно Кут повороту по осі OZ 270° ваного способу модель 11 буде орієнтована в такий спосіб 12 (Фіг.11), щоб досягти найкращої точності з наступними оптимальними кутами її повороту навколо осей координат. (табл. 2). Таблиця 2 Кут повороту по осі ОХ 0° Кут повороту по осі OY 90° У третьому випадку є модель кронштейна 13, зображена на Фіг.12, з габаритними розмірами по осях координат 114,300 х 76,200 х 93,662мм відповідно. У результаті застосування запропонованого Кут повороту по осі OZ 270° способу модель 13 буде орієнтована в такий спосіб 14 (Фіг.13), щоб досягти найкращої точності з наступними оптимальними кутами її повороту навколо осей координат. (табл. 3). 7 54398 8 Таблиця 3 Кут повороту по осі ОХ 0° Кут повороту по осі OY 90° Використання пропонованого способу дозволяє отримати найбільшу точність формоутворення виробів. Це досягається за рахунок того, що провадиться аналіз різних варіантів орієнтації виробу на робочій платформі й вибирається той варіант, при якому воно буде виготовлене з найкращими показниками якості поверхні створюваного виробу. Внаслідок цього, зменшується припуск під їхню остаточну обробку, а виходить, підвищується продуктивність процесу виготовлення виробів. Перевагою пропонованого способу являється також те, що для його здійснення може бути використаний найбільше простій, у порівнянні з аналогічними способами, метод. Поверхня моделі виробу не вимагає аналітичного опису, вона задана у вихідному STL-файлі, автоматично створюваним сучасними системами 3D CAD моделювання. Наступна перевага пропонованого способу полягає в тому, що даний спосіб вибору оптимальної орієнтації виробів на робочій платформі реалізований у програмі. Таким чином, відсутня необхідність у ручній праці оператора установки пошарового виготовлення виробів. Програма автоматично розраховує кути повороту виробів будьякої складності на підставі введеного значення кута повороту по осях координат. Джерела інформації: 1. Пат. 4863538 США, МПК В 27 N 3/00, В 32 В 31/00, В 23 К 9/00, В 29 С 67/00. Method and apparatus for producing parts by selective sintering / Carl R. Deckard; Board of Regents, The University of Texas System. - №920580; filed 17.10.1986; date of print 05.09.1989. 2. Пат. 5015424 США, МПК В 29 С 35/08. Methods and apparatus for production of threedimensional objects by stereolithography / Dennis R. Smalley; 3D Systems Inc. - №183015 ; filed 18.04.1988; date of print 14.05.1991. 3. Пат. 5130064 США, МПК В 29 С 35/08, В 29 С 41/02, В 29 С 41/52. Method of making a three dimensional object by stereolithography / Dennis R. Smalley, Charles W. Hull; 3D Systems Inc. №429435 ; filed 30.10.1989; date of print 14.07.1992. 4. Пат. 5141680 США, МПК В 29 С 35/08, В 29 С 41/02, В 29 С 41/36. Thermal stereolithography / Thomas A. Almquist, Dennis R. Smalley; 3D Systems Inc. - №592559; filed 04.10.1990; date of print 25.08.1992. 5. Пат. 5184307 США, МПК G 06 F 15/46, В 29 С 35/08, В 29 С 67/00. Method and apparatus for production of high resolution three-dimensional objects by stereolithography / Charles W. Hul, Stuart T. Spense, David J. Albert and other; 3D Systems, Inc. - №331644; filed 31.03.1989; date of print 02.02.1993. 6. Пат. 5247180 США, МПК В 29 С 35/08. Stereolithographic apparatus and method of use / Larry D. Mitcham, William E. Nelson; Texas Кут повороту по осі OZ 90° Instruments Incorporated. - №814859; filed 30.12.1991; date of print 21.09.1993. 7. Пат. 5437964 США, МПК G 03 С 5/00, G 03 С 1/725, G 08 F 2/46. Stereolithography using vinyl ether-epoxide polymers / Stephen С Lapin, James R. Snyder, Eugene V. Sitzmann and other; Allied-Signal Inc. - №201146; filed 24.02.1994; date of print 01.08.1995. 8. Пат. 5663883 США, МПК G 06 F 19/00. Rapid prototyping method / Charles L. Thomas, Zetain Wang; University of Utah Research Foundation. №517092; filed 21.08.1995; date of print 02.09.1997. 9. Пат. 5902538 США, МПК В 29 С 35/08, В 29 С 41/02. Simplified stereolithographic object formation methods of overcoming minimum recoating depth limitations / Theodor R. Kruges, Chris R. Manners, Hop D. Hguyen; 3D Systems, Inc. №08/920428; filed 29.08.1997; date of print 11.05.1999. 10. Пат. 6600965 Bl CILIA, МПК G 06 F 19/00. Method and apparatus for production of high resolution three-dimensional objects by stereolithography / Charles W. Hull, Stuart T. Spence, David J. Albert and other; 3D Systems Inc. №09/236259; filed 26.01.1999; date of print 29.07.2003. 11. Alexander P. Part orientation and build cost determination in layered manufacturing / P. Alexander, S. Allen, D. Dutta // Computer Aided Design. - 1998. - Vol. 30. - No. 5. - P. 343-356. 12. Bablani M. Quantification of errors in rapid prototyping processes and determination of preferred orientation of parts / M. Bablani, A. Bagchi // Transactions of the North American Manufacturing Research Institution of SME. - 1995. - Vol. 23. - P. 319-324. 13. Cheng W. Multi-objective optimization of partbuilding orientation in stereolithography / W. Cheng, J.Y.H. Fuh, A.Y.C. Nee, Y.S. Wong, H.T. Loh, T. Miyazawa // Rapid Prototyping J. -1995.-Vol. l.-No. 4.P. 12-23. 14. Frank D. Expert system-based selection of the preferred direction of build for rapid prototyping processes / D. Frank, G. Fadel // J. of Intelligent Manuf. - 1995. - No. 6. - P. 339-345. 15. Hong S. Byun. Determination of optimal build direction in rapid prototyping with variable slicing / Hong S. Byun, Kwan H. Lee // Int. J. Adv. Manuf. Technol. - 2006. - No. 28. -P. 307-313. 16. Hong S. Byun. Optimal part orientation of rapid prototyping using a genetic algorithm / Hong S. Byun, Kwan H. Lee // Proc. of the 34th Int. Conf. on Computers & Industrial Engineering. - 2004. - P. 426431. 17. Hur J. The development of a CAD environment to determine the preferred build-up direction for layered manufacturing / J. Hur, K. Lee // 9 Int. J. Adv. Manuf. Technol. - 1998. - No. 14.-P. 247254. 18. KimJ.Y., LeeK., ParkJ.C. Determination of optimal part orientation in stereolithographic rapid prototyping // Technical Report, Department of Mechanical Design and Production Engineering. Seoul: Seoul National University. - 1994. 19. LanP.T. Determining fabrication orientations for rapid prototyping with stereolithography apparatus / S.Y. Chou, L.L. Chent, D. Gemmill // ComputerAided Design. -1997. - Vol. 29. - No. 1.-P. 53-62. 20. Massod S.H. A generic algorithm for part orientation system for complex parts in rapid prototyping / S.H. Massod, W. Rattanawong, P. Iovenitti. - J. Mater. Process. Technol. - 2003. -Vol. 139.-Nos. 1-3.-P. 110-116. 21. Masood S.H. A generic part orientation system based on volumetric error in rapid prototyping / H.S. Masood, W. Rattanawong // Int. J. Adv. Manuf. Technol. - 2002. - No. 19. - P. 209-216. 22. Pandey P.M. Optimal part deposition orientation in FDM by using a multi-criteria Genetic Algorithm/ P.M. Pandey, K. Thrimurtullu, N.V. Reddy // Int. J. of Production Research. -2004. - Vol. 42. No. 19. - P. 4069-4089. 23. Pham D.T. Part orientation in stereolithography / D.T. Pham, S.S. Dimov, R.S. 54398 10 Gault // Int. J. Adv. Manuf. Technol. - 1999. - No. 15. P. 674-682. 24. Satyandra K. Gupta. Finding near-optimal build orientations for shape deposition manufacturing / Satyandra K. Gupta, Qi Tian, Lee E. Weiss // Proceedings of the IFIP TC5 WG5.3 Int. Conf. on Sculptured Surface Machining. - 1998. - Vol. 146. - P. 208-216. 25. Singhal S.K. Optimum part deposition orientation in stereolithography / S.K. Singhal, A.P. Pandey, P.M. Pandey, A.K. Nagpal // ComputerAided Design & Applications. - 2005. -Vol. 2. -Nos. 14.-P. 319-328. 26. Thompson D.C. Optimizing part quality with orientation / D.C. Thompson, R.H. Crawford // Proc. of the Solid Freeform Fabrication Symposium. - 1995. - Vol. 6. - P. 362-368. 27. Thrimurtullu K. Optimal part deposition orientation in fused deposition modeling / K. Thrimurtullu, P.M. Pandey, N.V. Reddy // Int. J. of Machine Tools and Manufacture. - 2003. -Vol. 44. No. 6. - P. 585-594. 28. Xu F. Optimal orientation with variable slicing in stereolithography / F. Xu, Y.S. Wong, H.T. Loh, J.Y.H. Fuh, T. Miyazawa // Rapid Prototyping J. 1997. - Vol. 3. - No. 3. - P. 76-88. 11 54398 12 13 54398 14 15 54398 16 17 Комп’ютерна верстка Л. Купенко 54398 Підписне 18 Тираж 26 прим. Міністерство освіти і науки України Державний департамент інтелектуальної власності, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601