Спосіб визначення зовнішньої питомої поверхні надтвердих дисперсних матеріалів
Номер патенту: 78937
Опубліковано: 25.04.2007
Автори: Петасюк Григорій Андрійович, Богатирьова Галина Павлівна, Новіков Микола Васильович
Формула / Реферат
1. Спосіб визначення зовнішньої питомої поверхні надтвердих дисперсних матеріалів, який передбачає вимірювання довжини проекції частинок надтвердого дисперсного матеріалу і визначення аналітичним шляхом показника зовнішньої питомої поверхні, який відрізняється тим, що додатково вимірюють ширину, площу та периметр проекції частинок надтвердого дисперсного матеріалу.
2. Спосіб за п.1, який відрізняється тим, що визначення показника зовнішньої питомої поверхні надтвердого дисперсного матеріалу здійснюють аналітичним шляхом за такою залежністю:
![]() ,
,
при цьому
![]() ,
,
![]() ,
, ![]() ,
,
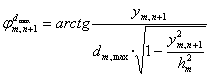 ,
, 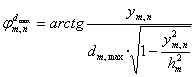 ,
,
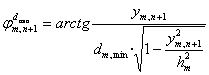 ,
, 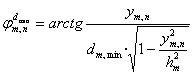 ,
,
![]() ,
,
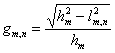 ,
,
де ![]() - показник зовнішньої питомої поверхні, м2/г,
- показник зовнішньої питомої поверхні, м2/г,
![]() - показник питомої густини, г/м3,
- показник питомої густини, г/м3,
![]() - кількість частинок надтвердого дисперсного матеріалу у пробі для аналізу, шт.,
- кількість частинок надтвердого дисперсного матеріалу у пробі для аналізу, шт.,
![]() - поточний номер частинки надтвердого дисперсного матеріалу в межах проби,
- поточний номер частинки надтвердого дисперсного матеріалу в межах проби,
- кількість відрізків, на які розбивається висота частинок надтвердого дисперсного матеріалу при чисельному визначенні їх площі поверхні і об'єму, шт.,
![]() - поточний номер відрізка, на які розбивається висота частинок надтвердого дисперсного матеріалу при чисельному визначенні їх площі поверхні і об'єму,
- поточний номер відрізка, на які розбивається висота частинок надтвердого дисперсного матеріалу при чисельному визначенні їх площі поверхні і об'єму,
![]() - периметр проекції частинки з номером m, мкм,
- периметр проекції частинки з номером m, мкм,
![]() - площа проекції частинки з номером m, мкм2,
- площа проекції частинки з номером m, мкм2,
![]() – об’єм конічного тіла, утвореного перетином частинки з номером m площинами, які проходять через дві суміжні точки розбиття (n та n+1) ) паралельно площині її проекції, мкм3,
– об’єм конічного тіла, утвореного перетином частинки з номером m площинами, які проходять через дві суміжні точки розбиття (n та n+1) ) паралельно площині її проекції, мкм3,
![]() - довжина проекції частинки з номером m, мкм,
- довжина проекції частинки з номером m, мкм,
![]() - ширина проекції частинки з номером m, мкм,
- ширина проекції частинки з номером m, мкм,
![]() - висота проекції частинки з номером m, мкм,
- висота проекції частинки з номером m, мкм,
![]() - дискретне (в точках розбиття) значення висоти частинки з номером m, мкм,
- дискретне (в точках розбиття) значення висоти частинки з номером m, мкм,
![]() - повний еліптичний інтеграл 2-го роду,
- повний еліптичний інтеграл 2-го роду,
![]() - модуль повного еліптичного інтегралу 2-го роду,
- модуль повного еліптичного інтегралу 2-го роду,
![]() - довжина дуг еліпсів, які є твірними конічних тіл, утворених перетином частинки з номером m площинами, які проходять через дві суміжні точки розбиття (n та n+1) паралельно площині її проекції, мкм,
- довжина дуг еліпсів, які є твірними конічних тіл, утворених перетином частинки з номером m площинами, які проходять через дві суміжні точки розбиття (n та n+1) паралельно площині її проекції, мкм,
![]() - коефіцієнт гомотетії (лінійного стиску).
- коефіцієнт гомотетії (лінійного стиску).
Текст
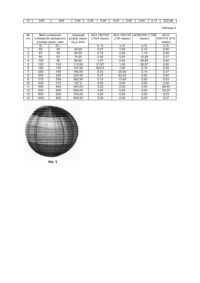
Винахід належить до методів діагностики характеристик порошків із надтвердих дисперсних матеріалів (синтетичних і природних алмазів, карбіду кремнію, кубічного нітриду бору та ін.), зокрема - їх зовнішньої питомої поверхні. Відомий спосіб визначення зовнішньої питомої поверхні надтвердих дисперсних матеріалів методом оптичного чи електронного мікроскопіювання [див. "Грег С,.Синг К. Адсорбция, удельная поверхность, пористость" / Пер. с английского под ред. К.В. Чмуто-ва. - М.: Мир, 1970, 407 с.], згідно з яким як геометричні характеристики вимірюють площу проекції частинок надтвердого дисперсного матеріалу. Потім обчислюють характерний розмір частинок, за який приймають еквівалентний діаметр і який визначається як діаметр круга, рівного за площею проекції частинки в напрямку, перпендикулярному площині найбільшої стійкості. Знаходять середній діаметр частинок для кожної фракції надтвердого дисперсного матеріалу як середнє арифметичне їх еквівалентного діаметру, а показник зовнішньої питомої поверхні визначають аналітичним шляхом за такою залежністю: Nf 2 å ni·dpi K = Fу д = · iN1 r f å i=1 (1) 3 ni·dpi де: K - фактор форми (безрозмірна величина); r - питома густина надтвердого дисперсного матеріалу, г/лґ; Nf - кількість фракцій надтвердого дисперсного матеріалу; i - номер фракції; nі - кількість фракцій надтвердого дисперсного матеріалу; dpi - середній діаметр частинок фракції з номером і, мкм. Для кубів і куль K= 6, для округли х частинок піску K= 6,1, для стертих частинок К= 6,4 і для загострених частинок K=7,7. Середній діаметр частинок надтвердого дисперсного матеріалу для фракції з номер / визначається як dpi = 1 ni ·å dpi , де d pik - еквівалентний діаметр частинок фракції з номером і, k - плинний ni k =i k їх номер. Практична реалізація цього способу базується на результатах вимірювання площі проекції частинок надтвердих дисперсних матеріалів, яке здійснюється з використанням мікроскопів. Такий спосіб визначення зовнішньої питомої поверхні надтвердих дисперсних матеріалів при відомих формі їх частинок і відповідному їй значенні фактора форми K забезпечує визначення зовнішньої питомої поверхні надтвердих дисперсних матеріалів із значно меншими матеріальними, економічними та трудовими затратами в порівнянні із способами, які ґрунтуються на фізичних вимірюваннях. Головним же недоліком цього способу є те, що він передбачає однотипність форми частинок порошку, що для реальних надтвердих дисперсних матеріалів не є реальним. Крім того спосіб дає велику похибку в порівнянні із способами, які базуються на проведенні вимірювання фізичних величин. Відомий найбільш близький за технічною суттю до винаходу спосіб визначення зовнішньої питомої поверхні надтвердих дисперсних матеріалів методом оптичного чи електронного мікроскопіювання (див. "Методы контроля дисперсности и удельной поверхности металлических порошков" / Паничкина В. В., Уварова И. В. - Киев: Наукова думка, 1973. - 167 с.), згідно з яким як геометричні характеристики вимірюють довжину проекції частинок порошку надтвердого дисперсного матеріалу. Потім проводять обчислення характерного розміру частинок, за який приймають середній їх розмір по кожній із виділених фракцій, а показник зовнішньої питомої поверхні визначають аналітичним шляхом за такою залежністю: Nf å ni·d2 i K i =1 Fу д = · N r f å ni·d3 i (2) i =1 де: K - фактор форми (безрозмірна величина); r - питома густина надтвердого дисперсного матеріалу, г/м ; Nf - кількість фракцій надтвердого дисперсного матеріалу; nі - кількість частинок надтвердого дисперсного матеріалу у фракції з номером і; і - номер фракції; di - середній розмір частинок надтвердого дисперсного матеріалу для фракції з номером і, мкм. Для звичайних дисперсних матеріалів, які мають кулеподібну чи близьку до неї полігональну форму частинок, K=6. Середній розмір частинок дисперсного матеріалу фракції з номером і визначається як di=(Di+Di+1)/2, де Di, Di+1 - відповідно ліва та права розмірні межі фракції з номером i. Практична реалізація цього способу базується на вимірюванні максимального лінійного розміру проекції частинок надтвердого дисперсного матеріалу, яким є довжина їх проекції. Вимірювання здійснюється методом оптичного чи електронного мікроскопіювання і разом із наступною математичною обробкою одержаних результатів складає сутність поняття мікроскопічний аналіз. Такий спосіб визначення зовнішньої питомої поверхні надтвердих дисперсних матеріалів при відомих формі їх частинок і відповідному їй значенні фактора форми К забезпечує визначення зовнішньої питомої поверхні таких матеріалів із значно меншими матеріальними, економічними та трудовими затратами в порівнянні зі способами, які ґрунтуються на фізичних вимірюваннях. Головним же недоліком цього способу, як і попереднього, є те, що він передбачає однотипність форми частинок порошку, що для реальних надтвердих дисперсних матеріалів є не реальним. Крім того спосіб дає велику похибку в порівнянні із способами, які базуються на проведені вимірювання фізичних величин. В основу винаходу поставлено завдання такого удосконалення способу визначення зовнішньої питомої поверхні надтвердих дисперсних матеріалів, при якому за рахунок додаткового вимірювання ширини та периметру проекції частинок надтвердого дисперсного матеріалу забезпечується більш точне визначення його зовнішньої питомої поверхні. Означене завдання вирішується завдяки тому, що у способі визначення зовнішньої питомої поверхні надтвердих дисперсних матеріалів, який передбачає вимірювання довжини проекції частинок надтвердого дисперсного матеріалу і визначення аналітичним шляхом показника зовнішньої питомої поверхні, згідно винаходу додатково вимірюють ширину, площу та периметр проекції частинок надтвердого дисперсного матеріалу, а визначення показника зовнішньої питомої поверхні надтвердого дисперсного матеріалу здійснюють за такою залежністю: 1 M N Sm,n Fпит . э = (3) å å r·M0 m=1 n =1Vm, n при цьому Sm, n = d d Immax + Idmin g( ym,n ) + g( ym, n +1) ,n m,n · ·Lm,0 2 2 d d max Immax = E(jm, n +1) - E(jmmax ) ,n ,n d Immin ,n d dmin = E(jmmin 1 ) - E(jm, n , n+ y2 , n+ 1 m dm, max · 1 h2 m ym, n = arctg dm, max · 1 dm, min· 1 2 ym, n h2 m y 2 ,n m 2 hm y m, n +1 = arctg d m, min · 1 h 2 - l2 ,n m m (7) y 2 , n +1 m h2 m ég 2 ( y m,n ) + g 2 ( y m,n +1 ) + ù Vm ,n = Sm,0 ·Dy m,n ·ê ú /3 ê + g ( ym,n ) + g( y m,n + 1) ú ë û g m,n = (6) ym , n d jmmin = arctg ,n d jmmin 1 , n+ (5) ) y m, n +1 j dmax 1 = arctg m, n + j dmax m, n , (4) (8) (9) hm де Fпит.з - показник зовнішньої питомої поверхні, м 2/г; r - показник питомої густини, г/м 3, М- кількість частинок надтвердого дисперсного матеріалу у пробі для аналізу, шт; m - плинний номер частинки надтвердого дисперсного матеріалу в межах проби; N - кількість відрізків, на які розбивається висота частинок надтвердого дисперсного матеріалу при чисельному визначенні їх площі поверхні і об'єму, шт; n - плинний номер відрізка, на які розбивається висота частинок надтвердого дисперсного матеріалу при чисельному визначенні їх площі поверхні і об'єму; Lm,0 - периметр проекції частинки з номером m, мкм; Sm,0 - площа проекції частинки з номером m, мкм 2, dm, max - довжина проекції частинки з номером m, мкм; dm, mi n - ширина проекції частинки з номером m, мкм; hm, mi n - висота проекції частинки з номером m, мкм ym,n - дискретне (в точках розбиття) значення висоти частинки з номером m, мкм; Е(m) - повний еліптичний інтеграл 2-го роду (див. Фихтенгольц Г. М. Курс дифференциального и интегрального исчисления. Т. П. -М.: Наука, 1969.- 800 с.; Двайт Г. Б. Таблицы интегралов и другие математические формулы / Перевод с английского под ред. К. А. Семендяева. - М.: На ука, 1977.- 224 с.); m - модуль повного еліптичного інтегралу 2-го роду (див. там же). Причинно-наслідковий зв'язок між сукупністю ознак, що заявляється, і технічними результатами, які досягаються при ії реалізації, полягає в наступному. Пропозиція додаткового одночасного вимірювання ширини, площі та периметру проекції частинок надтвердого дисперсного матеріалу позбавляє необхідності знання форми частинок і числової інформації про їх фактор форми. Крім того, використання досконалішої з погляду адекватності механічної моделі зерна та більш інформативного забезпечення наступного аналітичного розрахунку дозволяє значно наблизити розрахункові площу повної поверхні та об'єм окремої частинки до фактичних їх значень. Завдяки цьому досягається значне зменшення відносної похибки визначення зовнішньої питомої поверхні в порівнянні з її значенням, що доставляється відомими способами. Тим самим досягається значне наближення показника зовнішньої питомої поверхні до фактичного його значення. Але при цьому суттєво зменшуються затрати (часу, матеріальні, економічні, трудові), пов'язані з діагностикою зовнішньої питомої поверхні в порівнянні зі способами, які базуються на проведені вимірювання фізичних величин і дають найбільш близьке до фактичного значення показника цієї характеристики надтвердих дисперсних матеріалів. Приклади реалізації запропонованого способу визначення зовнішньої питомої поверхні надтвердих дисперсних матеріалів. Проводилось тестове визначення зовнішньої питомої поверхні шліфропорошків синтетичного алмазу АС4 160/125, АС6 63/50 та АС32 400/315 різними способами, а саме: 1) способом, що заявляється; 2) способом, який передбачає вимірювання тільки довжини проекції зерен і прийнятий за прототип; 3) способом, який передбачає вимірювання тільки площі проекції зерен; 4) методом квазістатичного фільтрування розрідженого газу на приладі ДУП-2 за прийнятою в сфері діагностики порошків синтетичного алмазу методикою (див. "Порошки и пасты из синтетических алмазов" / Ю. И. Никитин, С. М. Уман, Л. В. Коберниченко и др. -Киев: Наук. думка, 1992. - 284 с.). Цей метод базується на проведені вимірювання фізичних величин і доставляє найбільш близьке до фактичного значення показника зовнішньої питомої поверхні порошків синтетичного алмазу. Відбір проби порошку здійснювали після ретельного перемішування згідно з вимогами стандарту на вказаний надтвердий дисперсний матеріал (стандарту ДСТУ 3292 "Порошки алмазні синтетичні. Загальні технічні умови", введ. 01.01.96, Київ, Держстандарт України, 1995). Мікроскопічний аналіз шліфпорошку проводили на приладі DiaInspect.OSM виробництва фірми VOLLSTADT DIMANT GmbH (Німеччина). Технічні та комп'ютерно-програмні засоби цього приладу і асортимент морфометричних характеристик, які діагностуються на ньому, викладені в доступній науковотехнічній літературі по діагностиці надтвердих дисперсних матеріалів (див. "K вопросу повышение информативности морфологических характеристик порошков из сверхтвердых материалов, определяемых на видео-компьютерных диагностических комплексах" / Новиков Н. В., Богатырьова Г. П., Петасюк Г. А. Сверхтвердые материалы - 2005. - №3. - с. 73-85.). В нашому випадку використовуються такі характеристики як довжина, ширина, площа і периметр проекції частинок надтвердого дисперсного матеріалу та їх висота. Експериментальні значення показників цих характеристик для шліфпорошку АС4 160/125, одержаних на зазначеному приладі для перших 100 зерен подані в таблиці 1 (додається). Такий варіант ілюстрації має на меті дати зацікавленим можливість самостійно виконати подібні розрахунки, а також прослідкувати вплив величини проби зерен (їх кількості) на кінцевий результат, тобто на значення показника зовнішньої питомої поверхні. Згідно зі способом, що пропонується, чисельним методом проводилось визначення площі повної поверхні і об'єму кожного із зерен проби. При цьому виходили із механічної моделі зерна у вигляді еліпсоїдоподібного просторового тіла Т (див. фіг. 1), утвореного однопараметричним відображенням праобразу - замкнутої плоскої кривої. Фактичним прообразом цього відображення слугував контур (межа) зображення зерна (див. фіг. 2). В процесі вибору подібного механічного аналогу зерна виходили з того, що еліпсоїд є найбільш адекватною ідеалізованою прострово-геометричною його формою в задачах алмазноабразивної обробоки. До такого висновку приходили багато дослідників, які займались цією проблемою в різний час і результати досліджень яких опубліковані в доступних літературних джерелах. Відоме, наприклад, досить аргументоване обгрунтування вказаного вибору на користь саме еліпсоїду (див. "Модели формы зерен СТМ" / Лавриненко В. Й., Шепелев А. А., Петасюк Г. А. // Сверхтвердые материалы.-1994.- №5/6.- С. 18-21). Як теоретична основа конструювання вказаної механічної моделі зерна використовувався математичний апарат відображення афінного простору (див. "Отображение аффинного пространства в теории формообразования поверхностей резанием." / Перепелица Б. А. — Харьков: Высшая школа, 1981. - 107 с.). В нашому випадку відображення включало такі перетворення афінного простору: 1) плоску гомотетію (Гомотетією з центром О і коефіцієнтом g¹0 називається відображення площини r r r r на себе, при якому образ точки з радіус-вектором × r1 є така ж точка з радіус-вектором r і r = g × r .) 1 відносно системи координат (X,Y,Z) (див. фіг. 2), афінний параметр - коефіцієнт гомотетії g, швидкість його змінення Vg =const, зв'язок між афінним та незалежним (t) параметрами g=1+Vg t; 2) паралельний перенос відносно тієї ж системи координат в напрямку, що складає з осями Х1, Y1, Z1 кути p/2, 0 и p/2 відповідно, афінний параметр - довжина вектора переносу l, швидкість його змінення Vl=const, зв'язок між афінним та незалежним параметрами l=Vlt. Гомотетія і перенос здійснюються одночасно, їх параметри - функції одного і того ж незалежного параметру - часу t. Як незалежний параметр приймається довжина вектора переносу l, а коефіцієнт гомотетії g функціонально зв'язується з ним. Прообразом відображення виступає контур зображення зерна, яке спостерігається на дисплеї комп'ютера, тобто замкнута плоска лінія, для якої вводиться позначення П з. Площина, в якій лежить це зображення, суміщається із площиною Y=0 (див. фіг. 2). Оскільки аналітичне описання зображення зерна складає значні труднощі, то прообраз задається дискретно, у вигляді набору пар чисел, кожна із яких являє собою у, х координати зафіксованої кількості його точок. Процедура оцифрування контуру зображення зерна може бути здійснена за допомогою програмних засобів MatLab. Але значно простіше така задача розв'язується з використанням програми WINDIG. Плоска фігура, обмежена замкнутою кривою Пз, позначається через Ф0 (див. фіг. 2). Зв'язок між залежним і незалежним афінними параметрами для прийнятої механічної моделі зерна задається залежністю (коефіцієнтом гомотетії): h2 - l2 (10) h де h=c/2, с - висота зерна. Зауважимо, що процедура оцифрування здійснювалась лише для візуалізації прийнятої механічної моделі зерна. Обчислення об'єму та площі повної поверхні зерна проводиться лише з використанням наявної інформації про площу і периметр зображення зерна та його геометричні розміри. В оцифруванні контуру зображення при цьому необхідності не має, що є наслідком застосування математичного апарату відображення афінного простору. При чисельному визначенні сумарних об'єму та площі поверхні зерен висота тіла Т як просторовогеометричної моделі зерна ототожнюється з його висотою. Приймаючи до уваги симетрію тіла Т відносно площини Y=0, обмежувались обчисленнями тільки для однієї (верхньої) із двох його частин. Піввісь OY точками у0=0, у1,у2,..., уN-1, уN=h (N - число точок розбиття) ділилась на ряд відрізків. Довжина Dn кожного із таких відрізків визначалась як уn+1 - yn і була перемінною при переході від yn до уn+ 1 (n=1, 2,..., N). Критерієм добору значень Dn слугувала вимога, щоб різниця між відповідними цим yn, yn+1 значеннями хm,n та хm,n+1 не перевищувала фіксованої малої сталої величини є, тобто умова (хm,n - хm,n+1)£ e. Шляхом складання різниці xn-,n+1 та прирівнюванні її до e (найбільш несприятливий випадок) після відповідних перетворень була отримана залежність yn+1=f(yn) у вигляді: g= 2 æ y2 h ö Dyn +1 = yn - h - ç 1- n - e ÷ . (11) ç ç ÷ h2 a ÷ è ø Площинами, паралельними площині Y=0 і які проходять через точки у0, у1,у2,..., уN-1, уN , розглядувана частина тіла Т розділялась на ряд перетинів. Кожний такий перетин являє собою плоску фігур у, аналогічну фігурі F 0, але зменшену на коефіцієнт гомотетії (лінійного стиску). Два таких суміжних перетини утворюють просторове тіло - еліпсоїдоподібний пояс, верхня і нижня основи якого повторюють форму фігури F 0, оскільки одержані із неї шляхом гомотетії. При цьому відомі такі параметри фігури F о як площа (S0) та довжина (периметр, L0) її контуру, а також мінімальний (dmin) та максимальний (dmax) її розміри і висота (с) зерна. Вимірювання фактичних показників цих характеристик зерна проводилось на відео-комп'ютерному комплексі DiaInspect.OSM, призначеному для діагностики морфологічних характеристик абразивних порошків (мінімальний (Fmin) та максимальний (Fmax) діаметри Feret, площа проекції (А), периметр опуклого (Рc) та фактичного (Р) зображення, еліптичність, шорохатість контуру та ін.). По результатах вимірювання покладали: dmax=F max, min=Fmin, L 0=Р, S 0=А. Наближене визначення необхідних нам об'єму та бокової поверхні такого пояса здійснюємо, замінюючи його зрізаним конічним тілом з площами та периметрами нижньої і верхньої основи 2 Sn = S0·g (yn ) , L n = L 0·g( yn ) 2 та Sn+1 = S0·g2( yn+1) , (12) Ln+1 = L0·g( yn +1) відповідно та висотою Dn=yn+1-yn. Об'єм такого конічного тіла виражається формулою: ég 2 ( yn ) + g2 (y n +1 ) + ù Vn = S0 ·Dyn ·ê ú/3 ê+ g( yn ) + g( yn +1 ) ú ë û (13) де S0 - площа зображення зерна, яка визначається з використанням приладу DiaInspect.OSM. При обчисленні площі бокової поверхні еліпсоїдоподібних поясів виходили із того, що твірними зрізаного конічного тіла є дуги еліпсів. Відповідним вибором є похибку такої заміни можна звести до мінімуму. Довжину дуг еліпсів як твірних зрізаних не кругових прямих конусів знаходили чисельно, використовуючи аналітичне представлення еліптичних інтегралів 2-го роду (звичайного і повного) у вигляді нескінченного ряду. Вирахувані по залежності (3) і викладеному вище алгоритму значення зовнішньої питомої поверхні порошків, що аналізувались, приведені в таблиці 2 (додається). При N=100 на цю процедуру було затрачено 2,5 хвилини. Вказане значення N є оптимальним для порошків синтетичного алмазу, оскільки подальше його збільшення, як показали проведені нами дослідження, не приводить до відчутного уточнення значення зовнішньої питомої поверхні, а затрати часу на обчислення збільшуються. Проводилось також визначення показника зовнішньої питомої поверхні відомим способом з вимірюванням площі проекції (А ) зерен шліфпорошку досліджуваного надтвердогодисперсного матеріалу. Характерним розміром зерен в цьому випадку був їх еквівалентний діаметр, який визначався як dекв = 2· p·A . Числові значення меж фракцій і середнє значення еквівалентного діаметру зерен (dp) для тих із них, які попали в певну фракцію, подані в таблиці 3 (додається). Для забезпечення зіставлянності результатів числові значення меж фракцій приймались згідно згадуваного вище стандарту ДСТУ 3292-95. Показники зовнішньої питомої поверхні, визначені аналітичним шляхом за залежністю (1), приведені в таблиці 2 (додається). Паралельно проводилось визначення показника зовнішньої питомої поверхні відомим способом з вимірюванням довжини проекції зерен шліфпорошку досліджуваного надтвердого дисперсного матеріалу. Розділення порошку на фракції здійснювалось згідно з нормами стандарту ДСТУ 3292-95. Характерним розміром зерен в цьому випадку є їх середній розмір (dcp), який знаходився як dc=(Di+Di+1), де Di+Di+1 - межі виділених фракцій. Числові значення меж фракцій і середній розмір зерен для тих із них, які попали в певну фракцію подані в таблиці 4 (додається). Показники зовнішньої питомої поверхні, визначені аналітичним шляхом за залежністю (2), приведені в таблиці 2 (додається). Проводилось також визначення показника зовнішньої питомої поверхні на приладі ДУП-2 методом квазістатичного фільтрування розрідженого газу. Принцип роботи приладу оснований на вимірюванні коефіцієнта дифузії для кнудсенівського протікання газу при квазістаціонарному протіканні розрідженого газу через шари порошку. Перед вимірюванням питомої поверхні алмазний порошок прогрівався при температурі 200°С на протязі 1 години. Готувалась проба порошку в кількості 2,0 г. На дно ретельно протертої і очищеної спиртом від вакуумного мастила кювети вкладали акуратно вирізаний під внутрішній її діаметр кружок із фільтрувального паперу. Потім в кювету засипали порошок, на який зверху накладали ще один кружок фільтрувального паперу, а поверх її - металевий циліндр. Після цього кювета закріплювалась на вібраторі. Включали живлення вібратора, поступово збільшуючи напругу до ти х пір, поки візуально не спостерігалася вібрація порошку і металевого циліндру. Таким чином були одержані значення показника зовнішньої питомої поверхні, які подані в таблиці 2 (додається). Порівняння найбільш близького до фактичного значення показника зовнішньої питомої поверхні, яке доставляється методом квазістатичного фільтрування розрідженого газу на приладі ДУП-2 і передбачає вимірювання як фізичної величини коефіцієнта дифузії для кнудсенівського протікання газу із одержаними методом мікроскопіювання, дає підстави зробити наступні висновки. Відносна похибка визначення показника зовнішньої питомої поверхні відомими способами сягає 70% - 80%, що майже в 7-8 разів більше, ніж за способом, що пропонується. Тому ці способи можуть бути використані хіба що для досить наближеної, зі значною похибкою оцінки зовнішньої питомої поверхні надтвердих дисперсних матеріалів. Відносна ж похибка способу, що пропонується, не перевищує 11%, що є цілком допустимим в практиці визначення цієї характеристики шліфпорошків синтетичного алмазу. Таблиця 1 № п/п 1 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 Довжина, мкм 2 234,24 216,33 253,34 206,63 251,87 219,23 225,00 230,75 224,80 209,42 232,93 193,09 213,51 220,65 235,24 217,28 237,18 241,10 217,14 233,74 235,52 199,04 192,92 161,42 234,89 Геометричні параметри проекції зерен Ширина, мкм Висота, мкм Периметр, мкм 3 4 5 180,82 171,78 682,31 195,75 185,96 687,99 205,15 194,89 753,72 196,85 187,01 727,40 184,04 174,84 720,89 196,65 186,82 690,06 192,75 183,11 692,74 200,94 190,89 725,08 182,89 173,75 671,31 187,12 177,76 653,83 212,61 201,98 754,19 175,22 166,46 604,01 201,73 191,64 704,14 199,90 189,90 699,22 201,89 191,80 723,36 203,48 193,31 697,46 198,98 189,03 716,57 215,77 204,98 762,46 169,36 160,89 644,19 192,32 182,70 695,87 198,34 188,42 713,21 186,08 176,78 666,42 126,35 120,03 528,97 134,75 128,01 483,38 180,23 171,22 686,77 Площа, мкм 2 6 25474,52 26156,44 32921,50 25304,04 29124,95 25358,16 24895,43 28332,08 25964,31 25038,85 29901,58 20276,25 27520,27 24408,35 26849,18 28364,55 30009,82 27366,03 22010,81 29046,47 29928,64 23926,67 14274,28 13116,10 25569,23 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 202,33 126,36 212,09 314,46 289,07 184,60 162,51 221,01 181,68 213,61 181,41 244,43 204,75 178,43 165,01 248,02 167,46 212,30 180,95 203,30 232,05 206,74 222,40 212,29 202,48 217,28 193,09 236,51 270,26 220,64 259,91 204,49 56,62 221,62 257,80 220,28 52,31 164,52 221,32 161,10 207,67 231,99 234,28 237,27 255,46 40,88 196,52 221,88 233,84 252,63 220,32 248,21 214,39 236,05 296,61 196,86 186,15 229,73 31035,40 30513,14 22698,14 27487,80 34258,28 23020,15 195,56 77,19 194,43 221,88 184,35 170,16 134,48 184,65 128,57 190,58 120,41 163,31 163,38 159,89 130,36 164,02 133,61 185,81 172,45 192,93 206,33 197,91 166,91 176,15 185,16 180,18 180,36 204,30 241,05 176,10 208,34 183,60 50,82 198,29 223,51 197,93 47,16 116,38 209,40 123,68 179,73 213,31 206,99 210,60 232,92 28,71 180,40 206,78 217,44 174,99 183,12 228,58 187,94 214,21 184,40 172,47 166,11 212,87 238,57 253,44 221,01 252,90 251,40 211,98 185,78 73,33 184,71 210,79 175,13 161,65 127,76 175,42 122,14 181,05 114,39 155,14 155,21 151,90 123,84 155,82 126,93 176,52 163,83 183,28 196,01 188,01 158,56 167,34 175,90 171,17171,34 194,09 229,00 167,29 197,92 174,42 48,28 188,38 212,33 188,03 44,80 110.56 198,93 117.50 170,74 202,64 196,64 200,07 221,27 27,27 171,38 196,44 206,57 166,24 173,96 217,15 178,54 203,50 175,18 163,85 157,80 202,23 215,93 225,22 182,99 171,67 231,03 185,69 712,22 334,73 670,18 917,87 793,27 572,47 482,98 673.47 504,01 677,66 492,05 685,40 613,31 554,16 495,18 679,88 486,44 642,90 587,79 677,66 722,35 672,20 635,05 640,27 641,30 652,53 631,86 714,97 885,06 650,87 780,75 634,98 176,20 716,57 788,76 683,84 163,84 457,72 737,98 461,48 632,30 725,94 745,45 752,57 801,28 113,86 612,98 717,27 781,48 715,68 666,32 821,75 659,44 739,57 794,64 604,88 579,05 729,33 205,13 213,96 173,84 163,09 219,48 176,41 23263,70 5842,31 27173,90 38049,42 33075,74 22167,76 13727,66 25850,66 14980,55 22830,73 13199,99 20646,97 20232,95 17259,03 11987,69 26678,70 13684,37 25477,23 21691,50 25130,85 29974,64 28581,04 24746,60 22714,37 23704,78 25017,20 21531,84 31143,64 38606,86 24586,94 30699,85 23853,61 1877,98 25366,28 34629,00 28461,97 1612,791 11803,68 26245,74 11422,13 24189,16 31089,52 28992,35 30580,79 35273,04 752,28 22443,77 30367,01 30153,24 25447,46 24622,12 34580,29 26037,37 28894,93 36685,58 22487,07 19935,29 30034,17 747,45 787,59 662,24 705,01 807,23 657,98 90 91 92 93 94 95 96 97 98 99 100 21569,73 26811,30 25604,41 6459,28 21358,66 23214,99 28012,77 31176,11 23626,30 19951,52 26021,14 199,04 228,01 211,03 113,91 202,34 187,44 214,03 242,43 203,15 201,51 233,62 169,70 198,86 180,46 92,87 159,90 179,30 202,17 198,23 185,83 158,76 174,66 161,21 188,92 171,44 88,23 151,90 170,34 192,06 188,32 176,54 150,82 165,93 605,77 703,62 637,28 332,40 592,28 606,24 676,03 722,99 647,08 596,04 668,95 Таблиця 2 Об'єкт Випробов Марка, зернистість Показник Відносна Примітки випробувань ування № (мкм) шліфпорошку та питомої поверхні похибка, п/п кількість зерен (шт.) в шліфпорошку, % пробі м/кг Спосіб згідно 1 АС4,160/125 1524 36,18 2,22 Найменша похибка винаходу визначення показника питомої поверхні 2 АС4,160/125 100 31,56 14,59 Задовільна похибка визначення показника питомої поверхні 3 АС6,63/50 1700 69,49 10,90 Добра похибка визначення показника питомої поверхні 4 АС32,400/315 375 11,46 4,67 Дуже добра похибка визначення показника питомої поверхні Спосіб за 5 АС4,160/125 1524 7,39 80,00 Дуже велика похибка прототипом показника 6 АС4,160/125 100 7,44 79,88 визначення методика 7 АС6,63/50 1700 16,62 78,69 питомої поверхні Панічкіної Е 8 АС32,400/315 375 3,42 71,5 В. та Уварової І. В.) Спосіб за 9 АС4, 160/125 1524 9,22 75,00 Дуже велика похибка методикою показника 10 АС4,160/125 100 9,42 74,54 визначення Грега С. та 11 АС6, 63/50 1700 22,04 71,74 питомої поверхні Сінгха К. і 12 АС32,400/315 375 4,09 66,00 Спосіб 13 АС4,160/125 37,00 Найбільш точний спосіб фізичних визначення показника 14 АС4,160/125 37,00 вимірювань, фактичної зовнішньої питомої 15 АС6, 63/50 78,00 прилад ДУПповерхні порошків 16 АС32,400/315 12,00 2 синтетичних алмазів. Приймається як еталон для порівняння з іншими методами Таблиця 3 № п/п 1 2 3 4 5 6 7 8 9 10 11 Межі розмірних інтервалів АС4 160/100 середнього діаметру (1524 зерен) зерен, мкм Di Di+1 ni,% dp, мкм 50 40 0,67 43,61 63 50 0,00 0,00 80 63 0,27 74,84 100 80 0,80 90,71 125 100 3,47 116,39 160 125 8,40 145,00 200 160 71,73 181,63 250 200 12,67 209.13 315 250 0,00 0,00 400 315 0,00 0,00 500 400 0,00 0,00 АС4 160/100 (100 зерен) ni,% 2,00 0,00 0,00 2,00 3,00 9,00 74,00 9,00 0,00 0,00 0,00 dp, мкм 47,11 0,00 0,00 88,47 122,24 140,33 181,73 212,05 0,00 0,00 0,00 AC6 63/50 (1700 АС32400/315 (375 зерен) зерен) ni,% 1,10 8,00 58,62 31,03 0,69 0,14 0,00 0,00 0,00 0,00 0,00 dp, мкм 44,43 58,92 72,55 85,88 105,88 134,51 0,00 0,00 0,00 0,00 0,00 ni,% 0,00 0,27 0,00 0,00 0,27 0,00 0,27 0,80 0,53 35,47 60,27 dp, мкм 0,00 57,41 0,00 0,00 112,83 0,00 199,83 235,83 262,37 380,22 433,00 12 630 500 0,00 0,00 0,00 0,00 0,00 0,00 2,13 522,98 Таблиця 4 № п/п 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Межі розмірних інтервалів середнього розміру зерен, мкм Di Di+1 50 40 63 50 80 63 100 80 125 100 160 125 200 160 250 200 315 250 400 315 500 400 630 500 800 630 1000 800 середній розмір зерен (dcp), мкм 45,00 56,50 74,50 90,00 112,50 147,50 180,00 225,50 282,50 357,5 450,00 565,00 745,00 900,00 АС4 160/100 (1524 зерен) n i, % 0,27 0,13 0,40 1,07 21,87 66,53 8,53 0,27 0,13 0,00 0,00 0.00 0,00 0,00 АС4 160/100 AC663/50 (1700 АС32 (100 зерен) зерен) 400/315 (375 зерен) ni,% ni,% ni,% 1,00 0,14 0,00 2,00 1,10 0,00 0,00 15,59 0,27 0,00 48,69 0,00 1,00 28,97 0,00 1,00 5,10 0,00 20,00 0,14 0,27 62,00 0,00 0,00 13,00 0,00 0,53 0,00 0,00 2,40 0,00 0,00 66,40 0,00 0,00 29,33 0,00 0,00 0,53 0,00 0,00 0,27
ДивитисяДодаткова інформація
Назва патенту англійськоюMethod for determining the specific surface of superhard dispersed material
Автори англійськоюNovikov Mykola Vasyliovych, Bohatyriova Halyna Pavlivna, Petasiuk Hryhorii Andriiovych
Назва патенту російськоюСпособ определения удельной поверхности сверхтвердого дисперсного материала
Автори російськоюНовиков Николай Васильевич, Богатирева Галина Павловна, Богатырева Галина Павловна, Богатырёва Галина Павловна, Петасюк Григорий Андреевич
МПК / Мітки
МПК: G01N 15/02, G01N 15/08
Мітки: зовнішньої, спосіб, матеріалів, визначення, поверхні, дисперсних, питомої, надтвердих
Код посилання
<a href="https://ua.patents.su/9-78937-sposib-viznachennya-zovnishno-pitomo-poverkhni-nadtverdikh-dispersnikh-materialiv.html" target="_blank" rel="follow" title="База патентів України">Спосіб визначення зовнішньої питомої поверхні надтвердих дисперсних матеріалів</a>
Попередній патент: Спосіб одержання нітрит-нітратних солей
Наступний патент: Спосіб легування металу
Випадковий патент: Полотно підйомних воріт