Спосіб відновлення сигналу на вході датчика в умовах завад

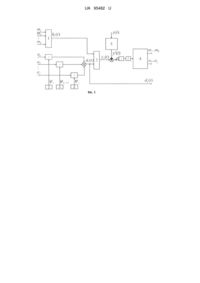
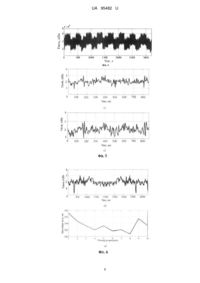
Реферат: Спосіб відновлення сигналу на вході датчика в умовах завад полягає в тому, що реалізацію вхідного сигналу представляють математичним рядом ортонормованих функцій з невідомими коефіцієнтами, імпульсну характеристику зводять до розподілу загального виду з невідомими коефіцієнтами, а потім мінімізують інтеграл від квадрата різниці між вихідним сигналом, що представляється через інтеграл згортки від імпульсної характеристики датчика та вхідного сигналу з невідомими коефіцієнтами і виміряним вихідним сигналом способами глобального випадкового пошуку, після чого знаходять всі невідомі коефіцієнти і на їх основі відновлюють імпульсну характеристику датчика і сигнал на його вході. У виміряному вихідному сигналі інерційного датчика відфільтровується завадоподібна складова, що дозволяє підвищити точність відновлення вхідного сигналу за рахунок зменшення впливу випадкових похибок вимірювань на якість перерахунку. UA 95482 U (12) UA 95482 U UA 95482 U 5 10 15 20 25 30 35 40 45 50 55 60 Корисна модель належить до обернених задач вимірювання і може застосуватися в галузях точного машинобудування для калібрування датчиків і підвищення точності вимірювальної інформації. Задачу відновлення невідомого сигналу, що пройшов через канал з невідомими характеристиками, називають задачею "сліпої" обробки сигналів. Розрізняють два основних типи таких задач: задача ідентифікації каналу і відновлення вхідного сигналу. Відомо багато способів ідентифікації каналів і відновлення вхідних сигналів в залежності від поставлених задач, наприклад, в книжці "Методы слепой обработки сигналов и их приложения в системах радиотехники и связи" (Горячкин, О.В. Методы слепой обработки сигналов и их приложения в системах радиотехники и связи. -М.: Радио и связь, 2003. - 230 с.) розглянуті питання теорії (приведені основні теореми "сліпої" ідентифікації) і практичного застосування методів "сліпої" обробки сигналів в задачах оцінки каналів зв'язку, в статті "Обратные задачи в измерительных процедурах" (Солопченко, Г.Н. Обратные задачи в процедурах/ Г.Н. Солопченко// Измерения, контроль, автоматизация. - 1983. - № 2 [46]. - С. 32-46) розглядаються методи "сліпої" обробки сигналів і ідентифікації, що застосовуються у вимірювальних процедурах. Спільним для описаних методів є застосування рівняння згортки для відновлення вхідного сигналу. Недоліком наведених способів є те, що для розв'язання задач "сліпої" обробки використовується інформація про вхідний сигнал, що зумовлює велику залежність результатів обробки від якості апріорної інформації. Найбільш близьким за суттю до заявленого є спосіб, що представлений в патенті "Спосіб відновлення сигналу на вході датчика" (Пат. 75106 Україна, МПК (2012.01) G01D21/00. Спосіб відновлення сигналу на вході датчика/ Полярус О.В., Поляков Є.О., Барчан В.В.; власник Харківський національний автомобільно-дорожній університет. № 201204273; заявл. 06.04.2012; опубл. 26.11.2012, Бюл. № 22, 6 с). Суть способу, який вибрано за найближчий аналог, полягає в тому, що реалізацію вхідного сигналу представляють математичним рядом ортонормованих функцій з невідомими коефіцієнтами, імпульсну характеристику зводять до розподілу загального виду з невідомими коефіцієнтами, а потім мінімізують інтеграл від квадрата різниці між вихідним сигналом, що представляється через інтеграл згортки від імпульсної характеристики датчика та вхідного сигналу з невідомими коефіцієнтами і виміряним вихідним сигналом способами глобального випадкового пошуку, після чого знаходять всі невідомі коефіцієнти і на їх основі відновлюють імпульсну характеристику датчика і сигнал на його вході, що дозволяє підвищити точність вимірювань за рахунок відновлення частини втраченої інформації. Недоліком найближчого аналога є залежність точності відновлення сигналу від наявності випадкових похибок вимірювання вихідного сигналу датчика. Даний вид похибок характерний динамічним вимірюванням і може бути обумовленим багатьма факторами, серед яких, наприклад шуми у вимірювальних каналах або властивості процесу вимірювань. Як зазначено у найближчому аналогу, на практиці вхідний сигнал датчика невідомий і безпосередньо оцінити точність відновлення інформації неможливо. Тому для оцінки точності перерахований сигнал можна порівнювати з результатами вимірювань більш точними (еталонними) малоінерційними вимірювальними приладами, робота яких ґрунтується на інших фізичних принципах. У запропонованому способі вихідний сигнал інерційного датчика перед перерахунком відфільтровується від завад. Задачею корисної моделі є підвищення точності вимірювальної інформації, яка може бути втраченою через наявність випадкових похибок динамічних вимірювань вихідного сигналу датчика при його відновленні на вхід за допомогою методу, що представлений у найближчому аналогу. Поставлена задача вирішується тим, що у відомому способі для знаходження вхідного сигналу за допомогою глобальних методів випадкового пошуку мінімізується функціонал, який являє собою інтеграл від квадрата різниці між теоретичним вихідним сигналом і виміряним. Теоретичний вихідний сигнал записується як згортка імпульсної характеристики датчика та вхідного сигналу. Останній має вигляд ряду з невідомими коефіцієнтами. Імпульсна характеристика описується математичною функцією з деякими невідомими коефіцієнтами. При мінімізації функціоналу отримуємо значення невідомих коефіцієнтів, що описують реалізацію випадкового процесу на вході датчика і імпульсну характеристику останнього. В корисній моделі знижується залежність від точності вимірювання вихідного сигналу датчика за рахунок фільтрації завадоподібних складових сигналу. На Фіг. 1 зображена схема реалізації запропонованого способу, на якій позначені: 1 функція, що описує загальний вигляд імпульсної характеристики, 2 - система ортонормованих функцій, 3 - блок згортки, 4 - блок пошуку глобального мінімуму функціоналу, 5 - блок фільтрації 1 UA 95482 U 5 виміряного інерційним датчиком сигналу. На Фіг. 2 зображена схема оцінки точності запропонованого способу, на якій позначені: 6 - еталонний датчик, 7 - інерційний датчик, 5 блок фільтрації вихідного сигналу інерційного датчика, 8 - блок перерахунку, 9 - блок порівняння. Для наведеного нижче прикладу на Фіг. 3 зображено залежність похибки відновлення вхідного сигналу датчика і коефіцієнта кореляції між точно виміряним сигналом і відновленим від величини випадкової похибки вимірювання вихідного сигналу. Спотворений інерційним датчиком сигнал y(t ) надходить до блока фільтрації, в якому відфільтровується завадоподібна складова сигналу, далі сигнал y' ( t ) потрапляє до системи перерахунку, в якій розраховуються вхідний сигнал dr ( t ) і імпульсна характеристика датчика 10 15 20 hr ( t ) . Вважаємо, що імпульсний відгук може бути записаний як функція загального вигляду (блок 1), в якій присутні невідомі параметри m1...mk , що характеризують його форму, а кожна реалізація випадкового вхідного сигналу може бути розкладена в ряд Карунена-Лоева. Випадкові коефіцієнти цього ряду a1...a j невідомі, а функції ряду є ортонормованими базисними і вибираються дослідником (блоки 2). Реалізація вихідного сигналу лінійного перетворювача потрапляє до блока згортки 3, на виході якого отримуємо сигнал yr ( t ) . Блок глобального випадкового пошуку (блок 4) мінімізує квадрат різниці між сигналами yr ( t ) і y' ( t ) шляхом змінювання невідомих коефіцієнтів сигналу та імпульсної характеристики при використанні генетичного алгоритму, який є відомим методом глобального випадкового пошуку екстремуму функції багатьох змінних. Сигнал y' ( t ) отримується на виході блока фільтрації (блок 5), на вхід якого потрапляє сигнал y(t ) , що виміряний інерційним датчиком. Після закінчення роботи генетичного алгоритму на вихід системи перерахунку надходить сигнал dr ( t ) , представлений рядом ортонормованих функцій зі знайденими випадковими коефіцієнтами a1...a j , що наближений до d(t ) . Вхідний сигнал d(t ) одночасно потрапляє на входи обох датчиків; еталонний датчик 6 дає 25 невеликі спотворювання вхідного сигналу, тому на виході отримаємо сигнал d1( t ) , який наближений до вхідного. На виході інерційного датчика 7, який можна описати, наприклад, за допомогою диференціального рівняння другого порядку, з'являється спотворений сигнал y(t ) з шумами, після чого він потрапляє на блок фільтрації 5; відфільтрований сигнал y' ( t ) потрапляє на вхід блоку перерахунку 8. На виході цього блока маємо розрахований вхідний сигнал dr ( t ) . 30 35 40 Для оцінки точності відновлення сигнали dr ( t ) і d1( t ) потрапляють на вхід блока порівняння 9, на виході якого отримуємо відносну похибку перерахунку в ідн і коефіцієнт кореляції К між сигналом, що вимірюється точним датчиком, і перерахованим вхідним сигналом. Приклад. Візьмемо, для прикладу, датчик тиску [Коваль А.О. Визначення постійної часу датчика при розв'язанні оберненої задачі вимірювань/ Коваль А.О., Котова А.І., Поляков Є.О., Полярус О.В./ Метрологія та прилади. - Харків: ВКФ "Фавор", 2014. С. 111-114]. Навіть при відсутності тиску, що обумовлений роботою технологічної лінії, на вході датчика завжди є гідравлічні шуми. Такі шуми можуть бути використані для визначення динамічних характеристик датчика. В експериментальній установці, що складається з ванни, яка частково заповнена водою, помпи, датчика тиску та системи трубопроводів з вентилями, здійснювався запис шумів та вхідних дій, що створювались шляхом переключення вентилів. На Фіг. 4 приведений приклад експериментальної реєстрації однієї з вхідних дій. Запис вихідного сигналу проведений для тривалого інтервалу часу (близько години). Невідома вхідна дія d(t) зв'язана з вихідним сигналом y(t ) лінійного інерційного датчика інтегралом згортки 45 y( t )    d( )h( t  )d , (1)  50 де h(t) - імпульсна характеристика датчика, яка на практиці майже завжди є невідомою. Крім того, в процесі експлуатації датчика вона змінюється і, отже, потребує корекції. Інтегральне рівняння згортки (1) розв'язується класичними методами тільки при точно відомих функціях h(t) та y(t ) . На жаль, вихідний сигнал y(t ) вимірюється з певними похибками, а 2 UA 95482 U імпульсну характеристику h(t) взагалі важко визначити. Тому виникла необхідність використання способу, який би враховував зазначені чинники. Таким способом є найближчий аналог. В ньому невідомий вхідний сигнал d(t) розкладається в ряд Карунена-Лоева: 5 i d( t )   aii , (2) i1 10 де i ( t ) - відомі ортогональні функції, наприклад, гармонічні функції; ai - невідомі коефіцієнти. Кількість членів ряду j визначається математичною складністю вхідної дії d(t) і коливається в межах від декількох одиниць до десятків одиниць. Для того, щоб визначити вхідну дію d(t) , необхідно оцінити невідомі коефіцієнти ai в (2). Для цього в запропонованому методі здійснюється мінімізація функціоналу T T j 0 0 i1 J  (a1, a2 ...a j )   [ y( t )   h( ) aii ( t  )d  n( t )]2dt . 15 20 25 Верхньою межею інтегралів Т є тривалість вхідної дії d(t) , що реєструється на виході датчика тиску. В квадратних дужках (3) представлена різниця між експериментально отриманим вихідним сигналом і цим же сигналом, але отриманим на основі рівняння згортки, де вхідна дія має вигляд (2). Отже, мінімізація функціоналу зводиться до мінімізації квадрата різниці між експериментальним та теоретичним сигналами на виході датчика. З математичної точки зору, це відстань у функціональному просторі між зазначеними сигналами. В ідеальному випадку підбором коефіцієнтів ai досягається, щоб ця відстань дорівнювала нулю. На практиці це неможливо. Для того, щоб посилити практичну значимість отриманих результатів, додатково в різницю між вказаними сигналами вводиться білий шум. Функціонал (3) залежить від багатьох аргументів at і його мінімізація здійснюється одним з основних методів стохастичного пошуку, який називається генетичним алгоритмом. Для мембранних датчиків тиску першого порядку перехідна характеристика найчастіше має вигляд, що описується функцією H( t )  U0 (1  e 30 (3)  t 0 (4) ), але навіть датчики другого порядку мають перехідну характеристику, що проходить через точку ( 0 , 0,632  U0 ) і наближається до U0 при t   . З виразу (4) визначаємо імпульсну характеристику датчика з врахуванням відомого зв'язку між імпульсною і перехідною характеристиками: t dH( t ) U0  0 . h( t )   e dt 0 (5) 35 Отже, будемо вважати, що імпульсна характеристика датчика тиску описується формулою (5), в якій невідомим параметром є тільки постійна часу 0 . Амплітуда U0 є відомою з експериментів, але для спрощення досліджень (наприклад, зменшення кількості змінних в функціоналі (3)) нормуємо її до одиниці і тоді функціонал (3) запишемо у вигляді 40  1T  j J  (a1,...a j, 0 )   [ y( t )   e 0  aii ( t  )d  n( t )]2dt . 0 0 i1 0 T 3 (6) UA 95482 U 5 10 15 20 25 30 35 40 Відсутність амплітуди U0 в функціоналі (6) легко буде компенсована значеннями коефіцієнтів ai . Тепер кількість змінних в функціоналі (6) порівняно з функціоналом (3) збільшилась на одну одиницю і становить j  1 . В процесі мінімізації функціоналу (6) будуть знайдені всі змінні ai та постійна часу датчика 0 , тобто буде відновлений вхідний сигнал d(t ) за формулою (2) та імпульсна характеристика датчика тиску за формулою (5). Зрозуміло, що тепер легко отримати і перехідну характеристику H( t ) за формулою (5). Якщо як вхідні дії використати експериментальні дані (Фіг. 4), то розв'язання оберненої задачі внаслідок великої тривалості вхідної дії T ускладнюється. Для визначення постійної часу датчика достатньо знати тільки реалізацію стаціонарного випадкового вихідного сигналу на обмеженому часовому інтервалі. Для сигналу (Фіг. 4) приклад такої реалізації зображений на Фіг. 5,а. Відновлений сигнал має вигляд, зображений на Фіг. 5,б. Проведемо аналіз Фіг. 5. З нього випливає, що вихідний сигнал (Фіг. 5,а) на дуже короткому часовому інтервалі має швидкі флуктуації, які передаються на вхід датчика при відновленні вхідної дії (Фіг. 5,б). Фактично таких швидких флуктуацій тиску на вході датчика тиску з фізичних міркувань не може бути. Вони з'явились на виході датчика внаслідок впливу шумів (наприклад, внутрішніх шумів датчика) та завад. На відміну від білого шуму n(t) , який присутній у виразах (3), (6), ці шуми можуть мати неширокий спектр. Задача відновлення вхідної дії в таких умовах є некоректною. Для зменшення зазначених шумів необхідно провести їх згладжування методом "ковзаючого вікна". При згладжуванні не повинні бути усунуті характерні флуктуації, що існували на вході датчика. На Фіг. 6,а зображений згладжений сигнал, а на Фіг. 6,б - результат відновлення вхідної дії датчика на часовому інтервалі 4 с. На Фіг. 6 в приведені результати розрахунку постійної часу датчика для 10 математичних експериментів за формулою (6). Розкид значень постійної часу обумовлений особливостями методу: наближеним розкладанням в ряд (2), оптимізацією функціоналу (6) з допомогою методу глобального випадкового пошуку та можливою слабкою нелінійністю датчика. Середнє значення постійної часу датчика склало 288 мс. Для оцінки постійної часу датчика тиску було проведене спрямоване експериментальне дослідження. Датчик тиску, що використовувався в експерименті, був аналогічний тому датчику, за допомогою якого проводились вимірювання вхідної дії (Фіг. 4, 5). Експериментальна установка складалась з товстостінної стальної труби з внутрішньою довжиною 500 мм і внутрішнім діаметром 70 мм. На одному торці труби закріплювався датчик тиску, а на іншому піропатрон, який після підриву створював тиск, близький до миттєвого. Таким тиском імітувалась вхідна дія, яка була близькою до дії типу "сходинка", що звичайно використовується при визначенні перехідної характеристики датчика. На Фіг. 7,а приведений результат експериментального визначення перехідної характеристики датчика тиску, яка підтверджує залежність (4). Флуктуації перехідної характеристики на Фіг. 7,а обумовлені шумами датчика. Згладжена перехідна характеристика показана на Фіг. 7,б, з якої визначається постійна часу датчика. Вона становить 295 мс і є близькою до теоретично визначеної (288 мс). Отже, з використанням запропонованого способу можуть бути отримані результати відновлення, що є близькими до експериментальних. ФОРМУЛА КОРИСНОЇ МОДЕЛІ 45 50 55 Спосіб відновлення сигналу на вході датчика в умовах завад, який полягає в тому, що реалізацію вхідного сигналу представляють математичним рядом ортонормованих функцій з невідомими коефіцієнтами, імпульсну характеристику зводять до розподілу загального виду з невідомими коефіцієнтами, а потім мінімізують інтеграл від квадрата різниці між вихідним сигналом, що представляється через інтеграл згортки від імпульсної характеристики датчика та вхідного сигналу з невідомими коефіцієнтами і виміряним вихідним сигналом способами глобального випадкового пошуку, після чого знаходять всі невідомі коефіцієнти і на їх основі відновлюють імпульсну характеристику датчика і сигнал на його вході, який відрізняється тим, що у виміряному вихідному сигналі інерційного датчика відфільтровується завадоподібна складова, що дозволяє підвищити точність відновлення вхідного сигналу за рахунок зменшення впливу випадкових похибок вимірювань на якість перерахунку. 4 UA 95482 U 5 UA 95482 U 6 UA 95482 U Комп’ютерна верстка В. Мацело Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601 7