Спосіб відновлення сигналу на вході датчика

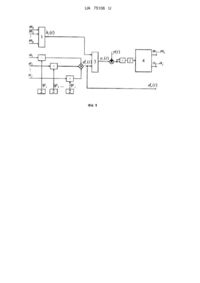
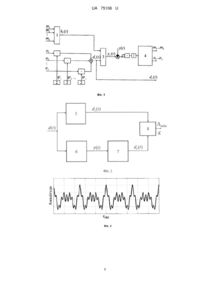
Реферат: Спосіб відновлення сигналу на вході датчика полягає в тому, що виміряний вихідний сигнал датчика виконаний у вигляді згортки невідомого вхідного сигналу і відомої імпульсної характеристики датчика, а сигнал на вході датчика визначають на основі розв'язання інтегрального рівняння згортки. Реалізацію вхідного сигналу представляють математичним рядом ортонормованих функцій з невідомими коефіцієнтами. Імпульсну характеристику зводять до розподілу загального виду з невідомими коефіцієнтами, а потім мінімізують інтеграл від квадрата різниці між вихідним сигналом, що представляється через інтеграл згортки від імпульсної характеристики датчика та вхідного сигналу з невідомими коефіцієнтами і виміряним вихідним сигналом способами глобального випадкового пошуку. Після цього знаходять всі невідомі коефіцієнти і на їх основі відновлюють імпульсну характеристику датчика і сигнал на його вході, що дозволяє підвищити точність вимірювань за рахунок відновлення частини втраченої інформації. UA 75106 U (12) UA 75106 U UA 75106 U 5 10 15 20 25 30 35 40 45 50 55 60 Корисна модель належить до обернених задач вимірювання і може застосовуватися в галузях точного машинобудування для калібрування датчиків і підвищення точності вимірювальної інформації. Задачу відновлення невідомого сигналу, що пройшов через канал з невідомими характеристиками, називають задачею "сліпої" обробки сигналів. Розрізняють два основних типи таких задач: задача ідентифікації каналу і відновлення вхідного сигналу. Відомо багато способів ідентифікації каналів і відновлення вхідних сигналів в залежності від поставлених задач, наприклад, в книжці "Методы слепой обработки сигналов и их приложения в системах радиотехники и связи" (Горячкин О.В. Методы слепой обработки сигналов и их приложения в системах радиотехники и связи. - М.: Радио и связь, 2003. - 230 с.) розглянуті питання теорії (наведені основні теореми "сліпої" ідентифікації) і практичного застосування методів "сліпої" обробки сигналів в задачах оцінки каналів зв'язку, в статті "Blind System Identification" (AbedMeraim, K. Blind System Identification / K. Abed-Meraim, W. Qiu, Y. Hua // IEEE Proceeding. - 1997. vol. 85. - P. 1310-1322) представлено деякі основні поняття і методи "сліпої" ідентифікації систем. Недоліком наведених способів є те, що для розв'язання задач сліпої обробки використовується інформація про вхідний сигнал, що зумовлює велику залежність результатів обробки від якості апріорної інформації. Найбільш близьким за суттю до заявленого є спосіб, представлений в статті "Обратные задачи в измерительных процедурах" (Солопченко Г.Н. Обратные задачи в измерительных процедурах / Г.Н. Солопченко // Измерения, контроль, автоматизация. - 1983. - № 2 [46]. - С. 3246), в якій розглядаються методи "сліпої" обробки сигналів і ідентифікації, що застосовуються у вимірювальних процедурах. Спільним для описаних методів є застосування рівняння згортки для відновлення вхідного сигналу. За найближчий аналог вибрано спосіб, що представлений на сторінці 34 "Розв'язання оберненої задачі в формулюванні (3)". Суть способу, який вибрано за найближчий аналог, складається у визначенні реалізації процесу на вході датчика, коли відомими є вихідний сигнал датчика та оператор, що характеризує його динамічні властивості, наприклад, імпульсна перехідна характеристика, яка відома точно. Спосіб полягає в тому, що вихідний сигнал датчика, який вимірюється, представляється у вигляді згортки вхідного сигналу і відомої імпульсної характеристики датчика, а сигнал на вході датчика визначається на основі розв'язання інтегрального рівняння згортки. Недоліком найближчого аналога є необхідність наявності точної математичної моделі (імпульсної характеристики) датчика. Розробники датчиків у більшості випадків таких характеристик не дають, оскільки внаслідок взаємодії датчика з об'єктом характеристики датчика можуть змінюватись. Чутливість методу до якості апріорної інформації може значно знижувати точність відновлення сигналу при наявності навіть невеликих неточностей в моделі імпульсної характеристики датчика. Для підвищення точності відновленого вхідного сигналу використовуються методи регуляризації і фільтрації, які в свою чергу також впливають на перерахований сигнал. На практиці вхідний сигнал датчика невідомий, тому оцінити точність відновлення інформації неможливо. Тому для оцінки точності перерахований сигнал можна порівнювати з результатами вимірювань більш точними (еталонними) малоінерційними вимірювальними приладами, робота яких ґрунтується на інших фізичних принципах. Для побудови їх моделі можна використати систему, яка представлена в роботі "Оптимальный прием сигналов" (Тихонов В.И. Оптимальный прием сигналов / В.И. Тихонов. - М.: Радио и связь, 1983. - С. 245252). Ця система використовує як засіб вимірювання пристрою, що випромінює електромагнітні хвилі, які можуть бути промодульовані механічними коливаннями об'єктів. Задачею корисної моделі є підвищення точності вимірювальної інформації, яка може бути втраченою через динамічні (інерційні) властивості датчика. Поставлена задача вирішується тим, що у відомому способі за допомогою рівняння згортки відновлюється частина втраченої вхідної інформації при умові наявності точної імпульсної характеристики датчика. В корисній моделі необхідність в точній імпульсній характеристиці відпадає. Достатньо мати уяву про загальний вигляд цієї характеристики, яка описується математичною функцією з деякими невідомими коефіцієнтами. Для знаходження вхідного сигналу за допомогою глобальних методів випадкового пошуку мінімізується функціонал, який являє собою інтеграл від квадрата різниці між теоретичним вихідним сигналом і виміряним вихідним сигналом. Теоретичний вихідний сигнал записується як згортка імпульсної характеристики датчика та вхідного сигналу. Останній має вигляд ряду з невідомими коефіцієнтами. При мінімізації функціоналу отримуємо значення невідомих коефіцієнтів, що описують реалізацію випадкового процесу на вході датчика і імпульсну характеристику 1 UA 75106 U 5 10 15 20 25 30 35 40 45 50 останнього. Для оцінки точності відновлення розрахований вхідний сигнал інерційного датчика порівнюється з вихідним сигналом більш точного датчика, який менше спотворює вимірювальну інформацію. Найчастіше цей датчик будується на іншому фізичному принципі. Крім того, при наявності можливості відновлений сигнал може порівнюватись з еталонним вхідним сигналом. Перелік фігур креслення. На фіг. 1 зображена схема реалізації запропонованого способу, на якій позначені: 1 - функція, що описує загальний вигляд імпульсної характеристики, 2 - система ортонормальних функцій, 3 - блок згортки, 4 - блок пошуку глобального мінімуму функціоналу (наприклад, генетичний алгоритм). На фіг. 2 зображена схема оцінки точності запропонованого способу, на якій позначені: 5 - еталонний датчик, 6 - інерційний датчик, 7 - блок перерахунку, 8 блок порівняння. Для наведеного нижче прикладу на фіг. 3 зображена реалізація вхідного випадкового сигналу, на фіг. 4 - залежність коефіцієнта кореляції між реалізаціями вхідного і перерахованого сигналів від відношення сигнал-шум при різній кількості невідомих коефіцієнтів ряду, що описує вхідний сигнал, на фіг 5 - залежність коефіцієнта кореляції між заданим і перерахованим вхідними сигналами від коефіцієнта кореляції між заданою імпульсною характеристикою і нею ж з заданою похибкою для існуючого (суцільна лінія) і запропонованого способів (пунктирна лінія). Спотворений інерційним датчиком сигнал y(t) надходить до системи перерахунку, в якій розраховуються вхідний сигнал dr(t) і імпульсна характеристика датчика hr(t). Якщо ця характеристика датчика невідома, оцінити вхідний сигнал неможливо. Таким чином, виникає необхідність використання апріорної інформації про деякі характеристики датчика. Зокрема, ми вважаємо, що імпульсний відгук може бути записаний як функція загального вигляду (блок 1), в якій присутні невідомі параметри m1…mk, що характеризують його форму, а кожна реалізація випадкового вхідного сигналу може бути розкладена в ряд Карунена-Лоева. Випадкові коефіцієнти цього ряду a1…aj невідомі, а функції ряду є ортонормованими базисними і вибираються дослідником (блоки 2). Реалізація вихідного сигналу лінійного перетворювача потрапляє до блока згортки 3, на виході якого отримуємо сигнал yr(t). Блок глобального випадкового пошуку (блок 4) мінімізує різницю між сигналами yr(t) і y(t) шляхом змінювання невідомих коефіцієнтів сигналу та імпульсної характеристики, яка також може розкладатись в ряд. Таким чином, знаходяться такі значення випадкових коефіцієнтів iмпульсної характеристики і вхідного сигналу, при яких розрахований вихідний сигнал максимально наближається до реального вихідного. Після закінчення роботи генетичного алгоритму на вихід системи перерахунку надходить сигнал dr(t), представлений рядом ортонормованих функцій зі знайденими випадковими коефіцієнтами a1…аj, що наближений до d(t). За допомогою цього алгоритму можна отримати всі необхідні коефіцієнти, тобто фактично розв'язати задачу "сліпої" обробки сигналів або оцінки сигналу на вході перетворювача. Вхідний сигнал d(t) одночасно потрапляє на входи обох датчиків; еталонний датчик 5 дає невеликі спотворювання вхідного сигналу, тому на виході отримаємо сигнал d 1(t), який наближений до вхідного. На виході інерційного датчика 6, який можна описати, наприклад, за допомогою диференціального рівняння другого порядку, з'являється спотворений сигнал y(t). Даний сигнал потрапляє на вхід блока перерахунку 7, в якому, як зазначено вище, знаходяться випадкові коефіцієнти, що описують випадковий процес на вході датчика. На виході блока перерахунку маємо розрахований вхідний сигнал dr(t). Для оцінки точності відновлення сигнали dr(t) і d1(t) потрапляють на вхід блока порівняння 8, на виході якого отримуємо відносну похибку перерахунку відн і коефіцієнт кореляції K між сигналом, що вимірюється точним датчиком, і перерахованим вхідним сигналом (розрахунок точності перерахунку наведено в таблиці). Як точний (еталонний) датчик будемо використовувати оптимальний радіолокаційний вимірювач вібрації машин. Приклад. Нехай на вхід системи надходить реалізація випадкового сигналу d(t) (приклад на фіг. 3), яка точно відома. Вважаємо, що форма імпульсного відгуку може бути записана як функція загального вигляду, наприклад, m1  m t2  t 2m1 1 exp 1 , t  0, m1  0,5, m2  0 , (1)  m2    де m1 ,m2 - невідомі параметри, які характеризують форму імпульсного відгуку. Реалізація вхідного сигналу в n-мірному представленні: hr t   2  m1    Г m1   m2    j dr t    ai  i t  . (2) i 1 55 У виразі (2) випадкові коефіцієнти аi цього ряду невідомі, а функції i(t) є ортонормованими базисними і вибираються дослідником. 2 UA 75106 U Реалізація вихідного сигналу лінійного перетворювача визначається рівнянням згортки y t     hr dr t  d  nt  , (3)  5 де h(t) - імпульсна характеристика датчика, і n(t) - адитивний випадковий процес (шум), який ми апроксимуємо білим гаусівським шумом. Беручи до уваги (1) і (2), вираз (3) можна записати наступним чином yt      10 j hr (r ) ai  i t   d  nt  . (4) i 1 У виразі (4) відомий вихідний сигнал y(t) і функції i(t). Цей вираз для даного випадку включає j+2 невідомих параметрів, серед них коефіцієнти аi є випадковими. Скорочення їх числа можливо у випадку, коли форма вхідного сигналу d(t) проста. Задача оцінки невідомих коефіцієнтів аi зводиться до задачі мінімізації функціонала   J a1,..., a j , m1, m 2  15 20 25 30 35 40 45 50    [ yt      j hr  a i  i t  d  nt ] 2 dt (5) i 1 для кожної реалізації вхідного сигналу і шуму. Вираз (5) містить різницю між відомим вихідним сигналом і його апроксимацією, що представлена сумою. Функціонал (5) містить j+2 невідомих параметрів: j коефіцієнтів ряду (2) і коефіцієнти m1, m2 функції (1). Отже, треба мінімізувати функцію багатьох параметрів. Досвід показує, що такі задачі найкраще розв'язуються за допомогою глобальних методів випадкового пошуку, наприклад, генетичних алгоритмів у випадках, коли відсутні вимоги щодо отримання результатів в реальному масштабі часу. Визначимо точність запропонованого способу. Після знаходження глобального мінімуму (5) визначаємо коефіцієнти ряду Карунена-Лоева a1…aj і параметри імпульсної характеристики m 1, m2 (1), а потім реалізацію розрахованого вхідного сигналу dr(t). На фіг. 4 представлена залежність коефіцієнта кореляції K між реалізаціями вхідного і перерахованого сигналів від відношення сигнал-шум при різній кількості невідомих коефіцієнтів ряду N, що описує вхідний сигнал dr(t). Після досягнення певного числа коефіцієнтів ряду збільшення коефіцієнта кореляції між вхідним і перерахованим на вхід датчика сигналами не відбувається. При відношенні сигналшум, що дорівнює п'яти, розрахунок забезпечує близькі до одиниці значення коефіцієнта кореляції, що вказує на високу схожість відновленого сигналу з реальним сигналом, що надходить на вхід датчика. Через те, що розрахунок вхідного сигналу існуючим способом при відсутності точної імпульсної характеристики неможливий, порівнювалась точність відновлення вхідного сигналу датчика запропонованим способом при умові наявності апріорної інформації про форму імпульсної характеристики з існуючим класичним способом при наявності точної імпульсної характеристики датчика. Порівняння точності відновлення вхідного сигналу існуючим і запропонованим способом при наявності похибок у вихідному сигналі датчика. При моделюванні задавалась окремо систематична похибка у вигляді гармонічного сигналу і випадкова у вигляді адитивного білого шуму. Відносна похибка перерахунку визначалась як відношення середньоквадратичного відхилення (СКВ) динамічної похибки перерахунку (різниця між заданим і перерахованим вхідними сигналами) до амплітуди вхідного сигналу. Результати розрахунку точності перерахунку вхідного сигналу запропонованим (при неточній імпульсній характеристиці) і існуючим способами при наявності динамічних похибок вимірювання вихідного сигналу представлені в таблиці. З наведених в таблиці результатів випливає, що у випадку відсутності похибок або при наявності систематичної похибки у вихідному сигналі, яка на два порядки менша амплітуди вхідного сигналу, існуючий спосіб забезпечує більш високу точність вимірювання. Це може бути обумовлене наявністю похибок визначення мінімуму цільової функції за допомогою генетичного алгоритму та похибками при апроксимації вхідного сигналу рядом Карунена-Лоева. При збільшенні систематичної похибки вихідного сигналу існуючий спосіб дає схожі результати із запропонованим. При наявності випадкових похибок проявляються фільтруючі властивості запропонованого способу. При відносних випадкових похибках вимірювання вихідного сигналу менших 10 % існуючий спосіб дає кращі результати, а при більших відношеннях сигнал-шум запропонований метод має в рази більшу перевагу по точності відновлення вхідного сигналу датчика. 3 UA 75106 U 5 10 15 20 Для порівняння запропонованого і існуючого способу розраховувалась точність відновлення сигналу в залежності від точності представлення імпульсної характеристики. Вимоги до точності заданої і розрахованої імпульсної характеристики датчика. При моделюванні розраховувався коефіцієнт кореляції між заданою імпульсною характеристикою і розрахованою при відновленні вхідного сигналу. Об'єм вибірки становив 1000. Середнє значення отриманої вибірки коефіцієнтів кореляції склало 0,95. При наявності точної апріорної інформації про форму імпульсної характеристики для запропонованого способу схожість відновлення імпульсної характеристики датчика постійна в певному діапазоні, тому на фіг. 5 коефіцієнт кореляції між вхідним і перерахованим сигналами зображений у вигляді пунктирної лінії, що не залежить від похибок представлення імпульсної характеристики датчика. Для порівняння даного способу з існуючим була розрахована залежність схожості між заданим і перерахованим вхідними сигналами, що виражена через коефіцієнт кореляції Kх, від схожості імпульсної характеристики, що виражена коефіцієнтом кореляції Kh між заданою імпульсною характеристикою і нею ж з заданою похибкою (фіг. 5) для iснуючого (суцільна лінія) і запропонованого способів (пунктирна лінія). З фіг. 5 можна зробити висновок про те, що точність відтворення вхідного сигналу існуючим методом вища лише за наявності точної імпульсної характеристики (коефіцієнт кореляції між відомою і реальною імпульсною характеристикою більший ніж приблизно 0,95). Спосіб дає можливість відновити частину втраченої вимірювальної інформації, тобто підвищити точність вимірювань. В порівнянні з існуючим способом, запропонований має на порядок більшу точність при наявності у вихідному сигналі датчика відносних випадкових похибок 10 % і більше, а також можливе відновлення вхідного сигналу датчика при наявності значних похибок імпульсної характеристики. Таблиця № п/п Відносна випадкова похибка, % 1 Сигнал без похибки Вихідний сигнал із систематичною похибкою 2 1 10 100 Вихідний сигнал з випадковою похибкою 3 1 10 100 Запропонований спосіб при наявності Існуючий спосіб при наявності апріорної інформації про форму точної імпульсної імпульсної характеристики характеристики Відносна похибка, Коефіцієнт Відносна Коефіцієнт % кореляції похибка, % кореляції -5 7,68 1,00 5,5·10 1,00 7,73 8,36 71,95 1,00 1,00 0,71 0,84 8,30 73,34 1,00 0,98 0,58 8,19 10,77 13,31 1,00 1,00 0,97 2,59 25,75 254,41 1,00 0,85 0,17 25 ФОРМУЛА КОРИСНОЇ МОДЕЛІ 30 35 40 Спосіб відновлення сигналу на вході датчика, який полягає в тому, що виміряний вихідний сигнал датчика виконаний у вигляді згортки невідомого вхідного сигналу і відомої імпульсної характеристики датчика, а сигнал на вході датчика визначають на основі розв'язання інтегрального рівняння згортки, який відрізняється тим, що реалізацію вхідного сигналу представляють математичним рядом ортонормованих функцій з невідомими коефіцієнтами, імпульсну характеристику зводять до розподілу загального виду з невідомими коефіцієнтами, а потім мінімізують інтеграл від квадрата різниці між вихідним сигналом, що представляється через інтеграл згортки від імпульсної характеристики датчика та вхідного сигналу з невідомими коефіцієнтами і виміряним вихідним сигналом способами глобального випадкового пошуку, після чого знаходять всі невідомі коефіцієнти і на їх основі відновлюють імпульсну характеристику датчика і сигнал на його вході, що дозволяє підвищити точність вимірювань за рахунок відновлення частини втраченої інформації. 4 UA 75106 U 5 UA 75106 U Комп’ютерна верстка В. Мацело Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601 6