Пристрій для порівняння даних, що представлені у непозиційній системі числення класу лишків

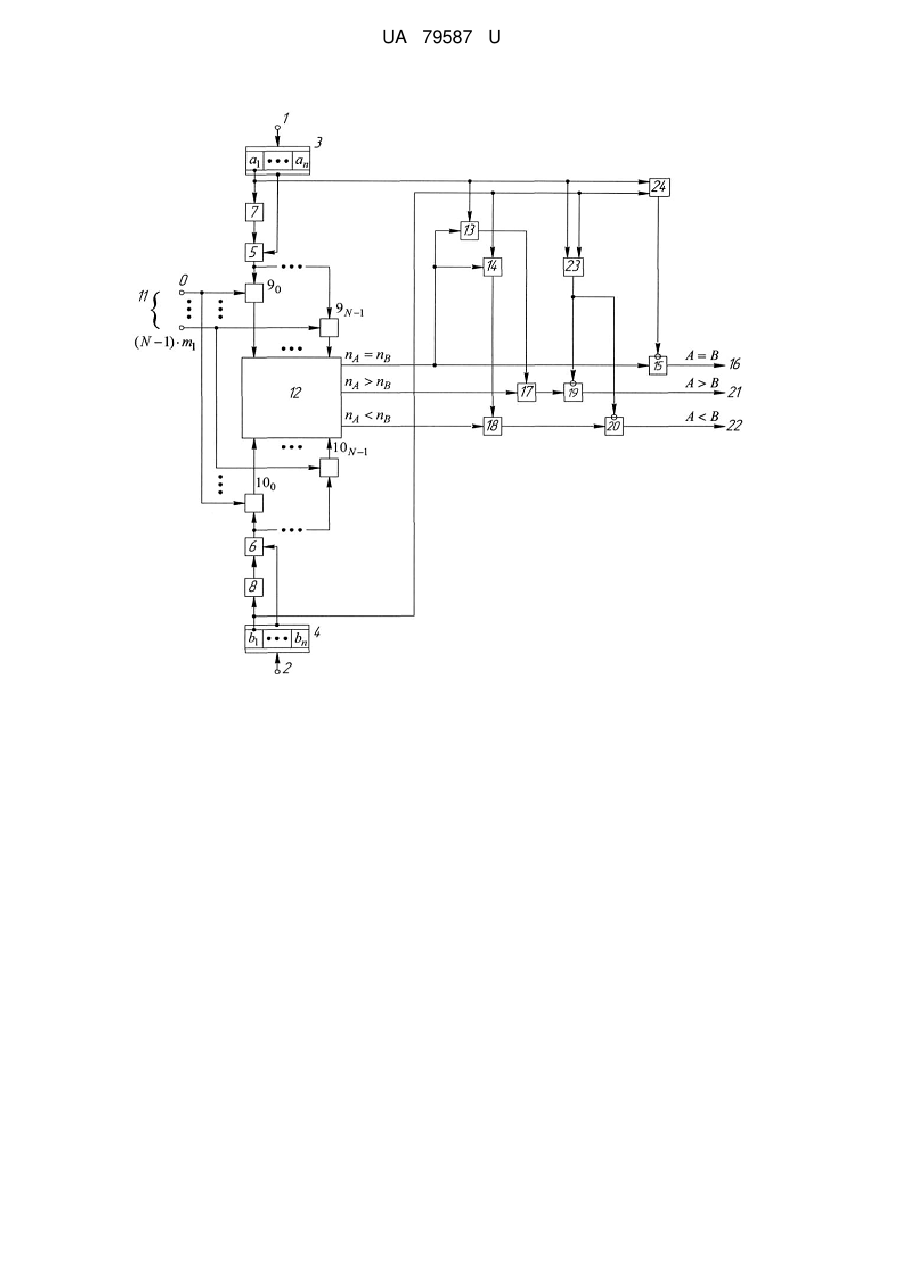
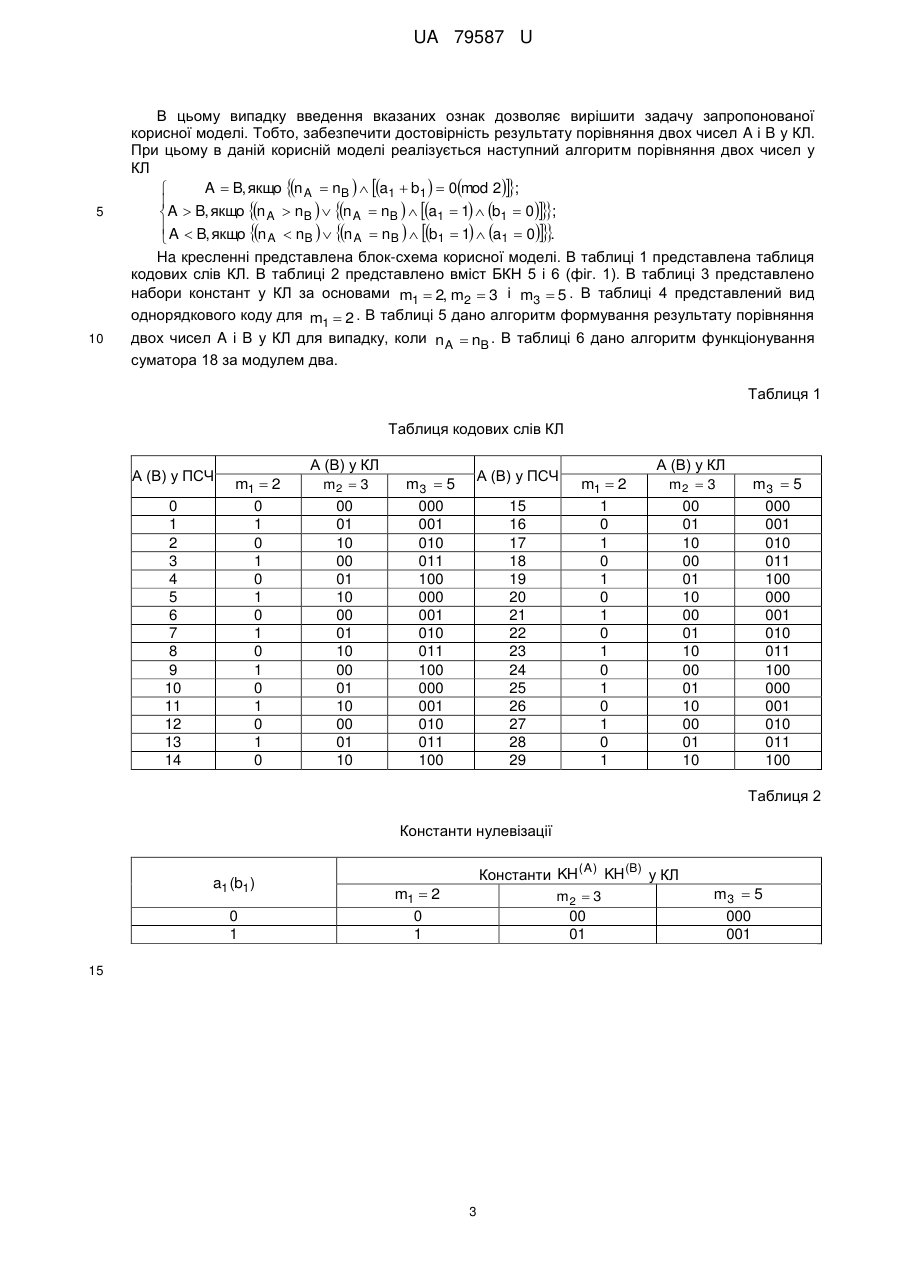
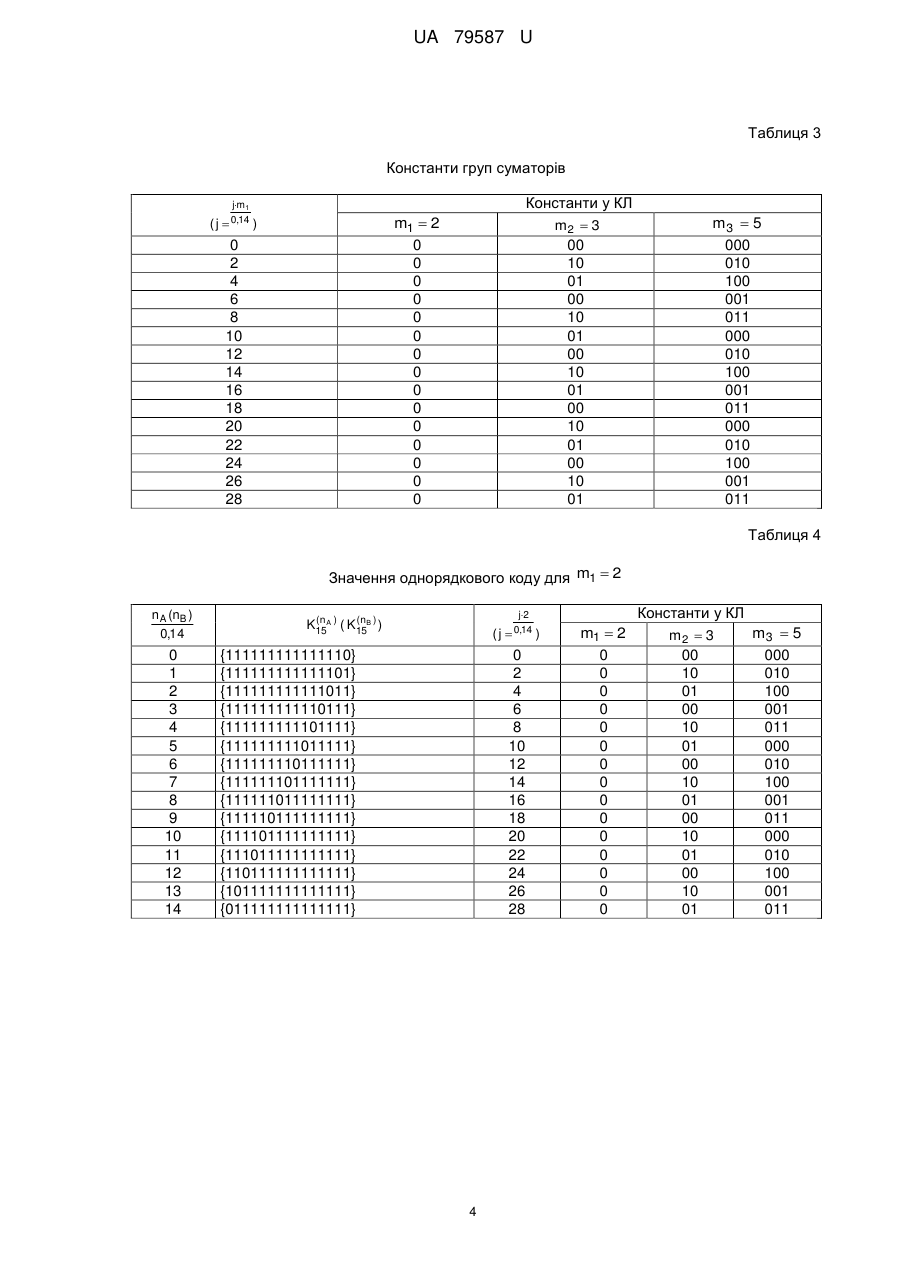
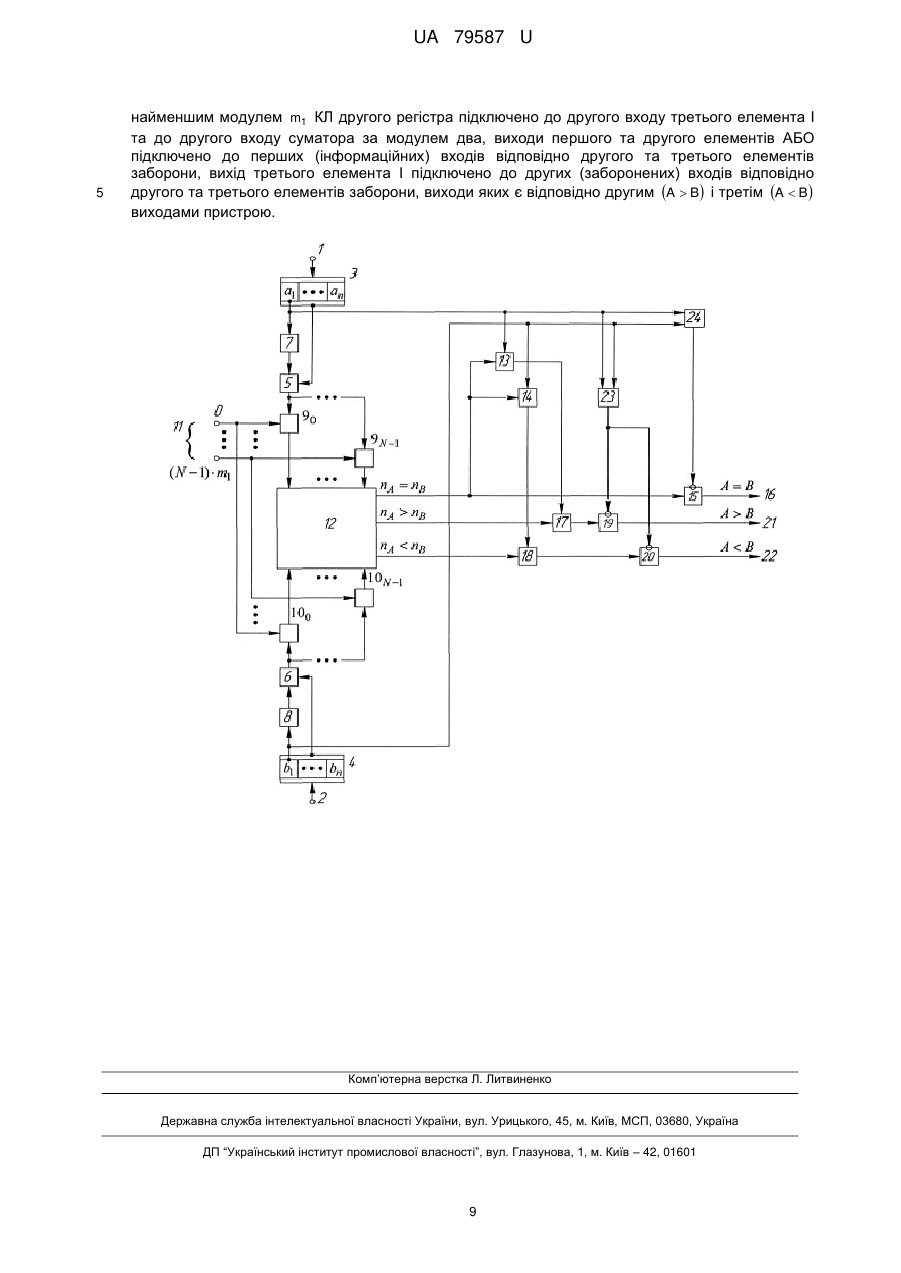
Реферат: Пристрій для порівняння даних, що представлені у непозиційній системі числення класу лишків, містить перший і другий вхідні регістри, перший і другий блоки констант нулевізації, перший і другий суматори, першу і другу групи суматорів, схему порівняння однорядкового коду, перший і другий елементи І, перший і другий елеменги АБО, перший елемент заборони, введені суматор за модулем два, другий та третій елементи заборони, третій елемент І. UA 79587 U (12) UA 79587 U UA 79587 U 5 10 15 20 25 30 35 40 45 50 55 Корисна модель належить до галузі автоматики та обчислювальної техніки і може бути застосована в інформаційно-телекомунікаційних та обчислювальних системах і мережах, що функціонують у непозиційній системі числення класу лишків (КЛ), а також при реалізації криптографічних перетворень у полях Галуа. Відомий пристрій (аналог) для порівняння чисел, що містить перший і другий вхідні регістри, перший і другий блоки констант, перший і другий суматори, першу і другу групи суматорів, схему порівняння однорядкового коду, елементи І, АБО, групу ключових елементів та ін. (а. с. СССР № 618739, кл. G 06 F 7/04, 1976 р.). Недолік даного аналога - низька достовірність результату порівняння. Також відомий пристрій (аналог) (а. с. СССР № 608155, кл. G 06 F 7/04, 1976 р.), що містить перший і другий вхідні регістри, перший і другий блоки констант, перший і другий суматори, першу і другу групи суматорів, схему порівняння однорядкового коду, елементи І, АБО та ін. Недолік даного аналога - низька достовірність результату порівняння. Близьким за технічною суттю до запропонованої корисної моделі (аналогом) є пристрій (а. с. СССР № 1037244, опубл. БВ № 31, 1983 р., G 06 F 7/04), де реалізується операція порівняння двох чисел у КЛ. Пристрій для порівняння чисел у класі лишків містить перший і другий вхідні регістри, перший і другий блоки констант нулевізації (БКН), перший і другий суматори, першу і другу групи суматорів, схему порівняння однорядкового коду (СПОК), причому, перший і другий входи пристрою підключено до входів відповідно першого та другого вхідних регістрів, виходи яких підключено до перших входів відповідно першого та другого суматорів, до других входів яких підключено виходи відповідно першого та другого блоків констант нулевізації, виходи першого та другого суматорів підключено до перших входів відповідно суматорів першої та другої груп, до других входів яких підключені шини подачі констант, виходи суматорів першої та другої груп підключено до перших і других входів СПОК. Недолік даного аналога - низька достовірність результату порівняння. Близьким за технічною суттю до запропонованої корисної моделі (аналогом) є пристрій для арифметичного порівняння чисел у КЛ (патент України на корисну модель № 64973, МПК G 06 F 7/04 (2006. 01), дата публікації 25.11.2011, Бюл. № 22). Пристрій містить перший і другий вхідні регістри, перший і другий блоки констант нулевізації, перший і другий суматори, першу і другу групи суматорів, схему порівняння однорядкового коду, перший і другий елементи І, перший та другий елементи АБО, при цьому, перший і другий входи пристрою підключено до входів відповідно першого та другого вхідних регістрів, виходи яких підключено до перших входів відповідно першого та другого суматорів, до других входів яких підключено виходи відповідно першого та другого блоків констант нулевізації, виходи першого та другого суматорів підключено до перших входів відповідно суматорів першої та другої груп, до других входів суматорів першої та другої груп підключені відповідні шини подачі констант виду ( 0,mn , 2  mn ,, N  1  mn ; 0,mn , 2  mn ,, N  1  mn модулі КЛ; 0,mn , 2  mn ,, N  1  mn кількість модулів КЛ; mi  mi 1 ), а виходи суматорів першої та другої груп підключено відповідно до перших і других груп входів схеми порівняння однорядкового коду перший n A  nB  вихід схеми порівняння однорядкового коду підключено до перших входів першого та другого елементів І, другий n A  nB  вихід схеми порівняння однорядкового коду підключено до першого входу першого елемента АБО, третій n A  nB  вихід схеми порівняння однорядкового коду підключено до першого входу другого елемента АБО. Недолік даного аналога - низька достовірність результату порівняння. Найбільш близьким за технічною суттю до запропонованої корисної моделі (прототипом) є пристрій для порівняння даних, що представлені у КЛ (патент України на корисну модель № 73379 України, МПК (2006.01) G 06F 7/04. Опубл. 25.09.2012, Бюл. № 18. Пристрій містить перший і другий вхідні регістри, перший і другий блоки констант нулевізації, перший і другий суматори, першу і другу групи суматорів, схему порівняння однорядкового коду, перший і другий елементи І, перший, другий та третій елемент АБО, елемент заборони, при цьому перший і другий входи пристрою підключено до входів відповідно першого та другого вхідних регістрів, виходи яких підключено до перших входів відповідно першого та другого суматорів, до других входів яких підключено виходи відповідно першого та другого блоків констант нулевізації, виходи першого та другого суматорів підключено до перших входів відповідно суматорів першої та другої груп, до других входів суматорів першої та другої груп підключені відповідні шини подачі констант виду 0,m1, 2  m1,, N  1  m1 ( N  n  mi ; i2 де m i модулі КЛ; n - кількість модулів КЛ; mi  mi 1 ), а виходи суматорів першої та другої груп 1 UA 79587 U підключено відповідно до перших і других груп входів схеми порівняння однорядкового коду перший n A  nB  вихід схеми порівняння однорядкового коду підключено до перших входів першого та другого елементів І, другий n A  nB  вихід схеми порівняння однорядкового коду 5 10 15 20 25 30 підключено до першого входу першого елемента АБО, третій n A  nB  вихід схеми порівняння однорядкового коду підключено до першого входу другого елемента АБО, вихід підрегістра лишку a1 за найменшим модулем КЛ m1 першого регістра підключено до входу першого блока констант нулевізації, до другого входу першого елемента І та до першого входу третього елемента АБО, а вихід підрегістра лишку b1 за найменшим модулем КЛ m1 другого регістра підключено до входу другого блока констант нулевізації, до другого входу другого елемента І та до другого входу третього елемента АБО, перший n A  nB  вихід схеми порівняння однорядкового коду підключено до першого (інформаційного) входу елемента заборони, до другого (забороненого) входу якого підключено вихід третього елемента АБО, вихід елемента заборони є першим A  B виходом пристрою, а виходи першого та другого елементів АБО є відповідно другим A  B і третім A  B виходами пристрою. Недолік прототипу - низька достовірність результату порівняння. Даний недолік полягає у тому, що корисна модель не в усіх випадках достовірно визначає результат операції порівняння двох чисел A і B у КЛ. Так, у випадку, коли n A  nB і a1  b1  1 , пристрій-прототип не вірно визначає результат операції. Цей недолік обумовлено тим, що загальний алгоритм порівняння двох чисел не ураховує всі можливі варіанти реалізації операції порівняння двох чисел у КЛ. Технічною задачею запропонованої корисної моделі є забезпечення достовірності результату порівняння двох чисел A і B у КЛ. Поставлена задача вирішується наступним чином. У пристрій для порівняння даних, що представлені у непозиційній системі числення класу лишків, який містить перший і другий вхідні регістри, перший і другий блоки констант нулевізації, перший і другий суматори, першу і другу групи суматорів, схему порівняння однорядкового коду, перший і другий елементи І, перший і другий елементи АБО, перший елемент заборони, при цьому перший і другий входи пристрою підключено до входів відповідно першого та другого вхідних регістрів, виходи яких підключено до перших входів відповідно першого та другого суматорів, до других входів яких підключено виходи відповідно першого та другого блоків констант нулевізації, виходи першого та другого суматорів підключено до перших входів відповідно суматорів першої та другої груп, до других входів суматорів першої та другої груп підключені відповідні шини подачі констант виду 0,m1, 2  m1,, N  1  m1 ( N  35 40 45 50 n  mi ; i2 де m1 - модулі КЛ; n - кількість модулів КЛ; mi  mi 1 ), а виходи суматорів першої та другої груп підключено відповідно до перших і других груп входів схеми порівняння однорядкового коду, перший n A  nB  вихід схеми порівняння однорядкового коду підключено до перших входів першого та другого елементів І та до першого (інформаційного) входу першого елемента заборони, вихід якого є першим A  B виходом пристрою, другий n A  nB  вихід схеми порівняння однорядкового коду підключено до першого входу першого елемента АБО, третій n A  nB  вихід схеми порівняння однорядкового коду підключено до першого входу другого елемента АБО, вихід підрегістра лишку a1 за найменшим модулем m1 КЛ першого регістра одночасно підключено до входу першого блока констант нулевізації та до другого входу першого елемента І, а вихід підрегістра лишку b1 за найменшим модулем m1 КЛ другого регістра одночасно підключено до входу другого блока констант нулевізації та до другого входу другого елемента І, а виходи першого та другого елементів І підключено до других входів відповідно першого та другого елементів АБО, додатково введено суматор за модулем два, другий та третій елементи заборони, третій елемент І, при цьому вихід підрегістра лишку a1 за найменшим модулем m1 КЛ першого регістра підключено до першого входу третього елемента І та до першого входу суматора за модулем два, вихід якого підключено до другого (забороненого) входу першого елемента заборони, а вихід підрегістра лишку b1 за найменшим модулем m1 КЛ другого регістра підключено до другого входу третього елемента І та до другого входу суматора за модулем два, виходи першого та другого елементів АБО підключено до перших (інформаційних) входів відповідно другого та третього елементів заборони, вихід третього елемента І підключено до других (заборонених) входів відповідно другого та третього елементів заборони, виходи яких є відповідно другим A  B і третім A  B виходами пристрою. 2 UA 79587 U 5 В цьому випадку введення вказаних ознак дозволяє вирішити задачу запропонованої корисної моделі. Тобто, забезпечити достовірність результату порівняння двох чисел A і B у КЛ. При цьому в даній корисній моделі реалізується наступний алгоритм порівняння двох чисел у КЛ A  B, якщо n A  nB   a1  b1   0mod 2;   A  B, якщо n A  nB   n A  nB   a1  1  b1  0;  A  B, якщо n  n   n  n   b  1  a  0 . A B A B 1 1  Ha кресленні представлена блок-схема корисної моделі. В таблиці 1 представлена таблиця кодових слів КЛ. В таблиці 2 представлено вміст БКН 5 і 6 (фіг. 1). В таблиці 3 представлено набори констант у КЛ за основами m1  2, m2  3 і m3  5 . В таблиці 4 представлений вид 10 однорядкового коду для m1  2 . В таблиці 5 дано алгоритм формування результату порівняння двох чисел A і B у КЛ для випадку, коли n A  nB . В таблиці 6 дано алгоритм функціонування суматора 18 за модулем два. Таблиця 1 Таблиця кодових слів КЛ А (В) у ПСЧ 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 m1  2 0 1 0 1 0 1 0 1 0 1 0 1 0 1 0 А (В) у КЛ m2  3 00 01 10 00 01 10 00 01 10 00 01 10 00 01 10 m3  5 000 001 010 011 100 000 001 010 011 100 000 001 010 011 100 А (В) у ПСЧ 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 m1  2 1 0 1 0 1 0 1 0 1 0 1 0 1 0 1 А (В) у КЛ m2  3 00 01 10 00 01 10 00 01 10 00 01 10 00 01 10 m3  5 000 001 010 011 100 000 001 010 011 100 000 001 010 011 100 Таблиця 2 Константи нулевізації a1 (b1) 0 1 Константи KH ( A ) KH (B) у КЛ m2  3 00 01 m1  2 0 1 15 3 m3  5 000 001 UA 79587 U Таблиця 3 Константи груп суматорів Константи у КЛ m2  3 00 10 01 00 10 01 00 10 01 00 10 01 00 10 01 jm1 m1  2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 ( j  0,14 ) 0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 m3  5 000 010 100 001 011 000 010 100 001 011 000 010 100 001 011 Таблиця 4 Значення однорядкового коду для m1  2 n A (nB ) 0,14 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 j2 (n (n K15A ) ( K15B ) ) ( j  0,14 ) {111111111111110} {111111111111101} {111111111111011} {111111111110111} {111111111101111} {111111111011111} {111111110111111} {111111101111111} {111111011111111} {111110111111111} {111101111111111} {111011111111111} {110111111111111} {101111111111111} {011111111111111} 0 2 4 6 8 10 12 14 16 18 20 22 24 26 28 4 m1  2 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 Константи у КЛ m3  5 m2  3 00 000 10 010 01 100 00 001 10 011 01 000 00 010 10 100 01 001 00 011 10 000 01 010 00 100 10 001 01 011 UA 79587 U Таблиця 5 Алгоритм формування результату порівняння двох чисел A і B у КЛ для n A  nB Перший n A  nB  вихід Послідовність елементів, що проходить сигнал від першого n A  nB  виходу Виходи пристрою СПОК 12 СПОК 12 до виходів пристрою a1 b1 Перший A  B 16 0 0 12-15-16 Третій A  B 22 0 1 12-14-18-20-22 1 0 1 1 Другий A  B 21 Перший A  B 16 12-13-17-19-21 12-15-16 Таблиця 6 Алгоритм функціонування суматора 24 за модулем два Входи суматора 24 за модулем два a1 b1 0 0 0 1 1 0 1 1 5 Вихід суматора 24 за модулем два 0 1 1 0 На кресленні представлена блок-схема корисної моделі, де 1, 2 - перший та другий інформаційні входи пристрою; 3,4 - перший та другий вхідні регістри, які складаються з n підрегістрів для зберігання лишків у двійковому коді відповідно першого A  a1, a2 ,, an  та другого B  b1,b 2 ,,bn  чисел, що порівнюються, за відповідними модулями mi, i  1, n КЛ; 5, 6 перший і другий суматори, що реалізують відповідно операції   1 A m1  A  a1  a1, a 2 ,, an   a1, a ,, a   0, a 1,, an  та 2 n 2 10   1 Bm1  B  b1  b1, b 2 ,, bn   b1, b ,, b   0, b 1,, bn  ; 7, 8 - перший і другий блоки 2 n 2 зберігання констант нулевізації (БКН); 9 0  9N1,10 0  10 N1 - перша та друга групи суматорів, що реалізують операції відповідно A m1  0  z 0 , A m1  m1  z1,, A m1  N  1  m1  z N1 , де N n  mi i2  та B m1  0  z  , B m1  m1  z1,, B m1  N  1  m1  z  1 (наприклад, для КЛ, що 0 N задано модулями m1  2,m2  3,m3  5,N  3  5  15 ); 11 - шини подачі значень констант виду 15 0, m1,2  m1, , N  1  m1 представлених у КЛ; 12 - схема порівняння однорядкового коду виду (n )  zN1, zN2 ,, z 0  та K N B  z 1, z 2 ,, z , де n A nB   0, N  1 - номер позиції нуля в N N 0 записі однорядкового коду (рахується справа наліво); 13, 14 - перший і другий елементи І; 15 перший елемент заборони (ЕЗ); 16 - перший A  B вихід пристрою; 17, 18 - перший, другий елементи АБО; 19, 20 - другий та третій елементи заборони; 21, 22 - другий A  B і третій A  B виходи пристрою; 23 - третій елемент І; 24 - суматор за модулем два. Перший 1 і другий 2 входи пристрою підключено до входів відповідно першого 3 та другого 4 вхідних регістрів, виходи яких підключено до перших входів відповідно першого 5 та другого 6 суматорів, до других входів яких підключено виходи відповідно першого 7 та другого 8 блоків констант нулевізації. Виходи першого 5 та другого 6 суматорів підключено до перших входів відповідно суматорів першої 9 0  9N1 та другої 10 0  10 N1 груп, до других входів яких (n ) KN A 20 25 підключені відповідні шини 11 подачі констант виду 0,m1, 2  m1,, N  1  m1 ( N  n  mi , де i2 mi модулі КЛ; n- кількість модулів КЛ; mi  mi1 ). Виходи суматорів першої 9 та другої 10 груп 5 UA 79587 U підключені відповідно до перших і других груп входів схеми 12 порівняння однорядкового коду   виду K N A  zN1, zN2 ,, z 0  та K N B  zN1, zN2 ,, z . Перший n A  nB  вихід схеми 12 0 порівняння однорядкового коду підключено до перших входів першого 13 та другого 14 елементів І, а також до першого (інформаційного) входу елемента 15 заборони, вихід 16 якого є першим A  B виходом пристрою. Другий n A  nB  вихід схеми 12 порівняння однорядкового (n ) 5 10 15 20 25 (n ) коду підключено до першого входу першого 17 елемента АБО, а третій n A  nB  вихід схеми 12 порівняння однорядкового коду підключено до першого входу другого 18 елемента АБО. Виходи першого 13 та другого 14 елементів І підключено до других входів відповідно першого 17 та другого 18 елементів АБО, виходи яких підключено до перших (інформаційних) входів відповідно другого 19 та третього 20 елементів заборони, виходи яких є відповідно другим 21 A  B і третім 22 A  B виходами пристрою. Вихід підрегістра лишку a1 за найменшим модулем КЛ m1 першого 3 регістра підключено до входу першого 7 блока констант нулевізації, до другого входу першого 13 елемента І, до першого входу третього 23 елемента І і до першого входу суматора 24 за модулем два, а вихід підрегістра лишку b1 за найменшим модулем КЛ m1 другого 4 регістра підключено до входу другого 8 блока констант нулевізації, до другого входу другого 14 елемента І, до другого входу третього 23 елемента І і до другого входу суматора 24 за модулем два, вихід якого підключено до другого (забороненого) входу першого елемента 15 заборони. Процес функціонування корисної моделі для порівняння двох чисел A  a1, a 2 ,, an  і B  b1, b 2 ,, bn  зручно представити у наступному вигляді. Через перший 1 та другий 2 входи пристрою перше A  a1, a 2 ,, an  та друге B  b1, b 2 ,, bn  числа (числа A та B представлені в КЛ сукупністю лишків, що представлені у двійковому коді), що порівнюються, надходять відповідно до першого 3 та другого 4 вхідних регістрів. За значеннями a1 і b1 у відповідних БКН 7 і 8 вибираються значення a1, a , a ,, a  і 2 3 n Суматори 5 та 6 здійснюють операції відповідно b1, b2 , b3 ,, bn  .    b , b ,, b   b , b ,, b   0, b  ,, b    . На перші входи суматорів першої 9 1 1 A m1  a1, a 2 ,, an   a1, a ,, a   0, a 1, a3  , an  та 2 n 2 Bm1 1 2 n 1 2 n 1 2 1 n 0  9N1 , групи надходять значення A m1 , а на перші входи суматорів другої 10 0  10 N1 групи надходять значення B m1 . На другі виходи суматорів першої 9 0  9N1 та другої 10 0  10 N1 груп по шинах 30 11 надходять значення констант виду 0,m1, 2  m1, 3  m1,, N  2  m1, N  1  m1 , де N  n  mk . k 2 Вихідні сигнали суматорів першої 9 0  9N1 групи утворюють однорядковий код (ОК) виду (n ) K N A  zN1, zN2 ,, z 2 , z1, z 0 . При цьому z nA  0 , якщо A m1  n A  m1  0 та z nA  1 , якщо A m1  n A  m1  0 . Вихідні сигнали суматорів другої 10 0  10 N1 групи утворюють ОК виду (n ) K N B  z 1, z 2 ,, z , z1, z . При цьому z nB  0 , якщо B m1  nB  m1  0 та z nB  1 , якщо N N 2  0 35 Bm1  nB  m1  0 для КЛ, . Таким чином вихідні сигнали суматорів першої 9 0  9N1 (другої що задано модулями n  m1  2, m2  3, m3  5 , 100  10N1 створюють ОК ) груп виду n  B K N A  zN1, zN2 ,, z 0   K15A   0 111 (K N B  z 1, z 2 ,, z   K15   0 111) , 111 111 N N 0 (n ) (n ) де n A nB   0, N  1 - ознака позиції знаходження нуля в запису ОК, яка чисельно дорівнює n  (K nB  ) . Таким чином на перші та 15 n  n  другі групи входів схеми 12 порівняння ОК надходить значення відповідно ОК K A і K B . номеру (рахується справа наліво) позиції нуля в ОК K15A 40 15 15 n A  nB , пристрій функціонує у відповідності з алгоритмом, що представлено таблицею 5. Сигнал першої n A  nB  вихідної шини схеми 12 надходить до перших входів елементів І 13 і 14, а також надходить до першого (інформаційного) входу першого елемента 15 заборони. Елемент 15 заборони відкрито, якщо відсутній вихідний сигнал У випадку коли 45 заборони суматора 24 за модулем два a1  b1   0mod 2 , 6 тобто у випадку якщо a1  b1  0 , UA 79587 U або a1  b1  1 . В цьому випадку сигнал першої вихідної шини схеми 12 надходить до першого 5 10 16 виходу A  B пристрою. В останніх випадках ( a1  1 b1  0 та a1  0, b1  1) перший , елемент 15 заборони закрито, так як присутній вихідний сигнал суматора 24 за модулем два a1  b1   1mod 2 . Елементи 19 і 20 заборони відкриті у випадку, коли відсутній сигнал заборони третього 23 елемента I ( a1  b1  0, a1  1 b1  0 та a1  0, b1  1), і елементи 19 і 20 , заборони закриті у випадку, коли присутній сигнал заборони третього 23 елемента І ( a1  b1  1 . Якщо a1  1 і b1  0 , тоді відкрито перший 13 елемент І, вихідний сигнал якого через перший 17 елемент АБО, через відкритий другий 19 елемент заборони надходить до другого 21 виходу A  B пристрою. Якщо a1  0 і b1  1, тоді відкрито другий 14 елемент І, вихідний сигнал якого через другий 18 елемент АБО, через відкритий третій 20 елемент заборони надходить до третього 22 виходу A  B пристрою. У випадку коли n A  nB , сигнал другої n A  nB  вихідної шини схеми 12 через перший 17 елемент АБО, через відкритий (відсутній вихідний сигнал заборони третього 23 елемента І) другий 19 елемент заборони надходить до другого 21 виходу A  B пристрою. 15 У випадку коли n A  nB , сигнал третьої n A  nB  вихідної шини схеми 12 через другий 18 елемент АБО, через відкритий (відсутній вихідний сигнал заборони третього 23 елемента І) третій 20 елемент заборони надходить до третього 22 виходу A  B пристрою. Розглянемо конкретні числові приклади порівняння чисел у КЛ, що заданий модулями m1  2,m2  3 і m3  5 (фіг. 1, таблиці 1-6). 20 Приклад 1. Нехай A 21  1 00, 001 і B24  0, 00, 100  (табл. 1). За значенням a1  1b1  0 ,   , у БКН 7 (8) вибирається KH (табл. 2) виду KH A   1 01, 001 KH B   0, 00, 000  . Суматор 5 (6) реалізує операцію (табл. 1, 2) A 21  KHA   1 00, 001  1 01 001  0, 10, 000 B24  KHB   0, 00, 100  0, 00, 000  0, 00, 100 , , , . Значення 0, 10, 100  і 0, 00, 100  з виходів відповідних суматорів 7 і 8 надходить на перші входи відповідно суматорів першої 9 і другої 10 груп. На другі входи суматорів 9 і 10 груп по шинам 11 надходять сигнали, що відповідають значенню констант 0, m1,2  m1,3  m1,,14  m1  25 (тобто m1  j , для n   j  0, N  1 m1  2 ) (табл. 3). З виходів суматорів 9 сформований ОК ; 10 K 15A  K 15    1111011111 11111 (табл. 4) надходить на першу групу входів СПОК 12. З n  30 12 виходів суматорів 10 ОК виду K15B  K15    1101111111 11111 (табл. 4) надходить на другу групу входів СПОК 12. Так як n A  10  nB  12 , тоді на третьому n A  nB  виході СПОК 12 присутній вихідний сигнал, який через елемент АБО 18, ЕЗ 20 надходить до виходу 22 пристрою. Це свідчить про те що A 21  B 24 . Приклад 2. Нехай A 21  1 00, 001 і B20  0, 10, 100  . За значенням a1  1b1  0 у БКН 7 ,  35  , (8) вибирається KH (табл. 2) виду KH A   1 01, 001 KH B   0, 00, 000  . Суматор 5 (6) реалізує операцію (табл. 1, 2) A  KH A   1 00, 001  1 01, 001  0, 10, 000  B  KH B   0, 10, 000   0, 00, 000   0, 10, 000  . , ,  21  20 Значення 0, 10, 100  і 0, 10, 000  з виходів відповідних суматорів 7 і 8 надходить на перші входи відповідно суматорів першої 9 і другої 10 груп. На другі входи суматорів 9 і 10 груп по шинам 11 надходять сигнали, що відповідають значенню констант 40 0, m1,2  m1,3  m1, ,13  m1,14  m1 ; (тобто m1  j , для j  0, N  1 m1  2 ), (табл. 3). З виходів суматорів 9 сформований ОК n A   K 10     K15 1111011111 11111 15 (табл. 4) надходить на першу групу входів СПОК 12. З виходів n  10 суматорів 10 ОК виду K15B  K15    1111011111 11111 (табл. 4) надходить на другу групу входів СПОК 12. Так як n A  nB  10 , тоді на першому n A  nB  виході СПОК 12 присутній вихідний сигнал, який через відкритий a1  1 елемент I 13, елемент АБО 17, ЕЗ 19 надходить 45 до другого 21 виходу A  B пристрою. Це свідчить про те що A 21  B 20 . 7 UA 79587 U Приклад 3. Для випадку коли n A  nB B 21  1 00, 001 . За значеннями a1  1 і b1  1 у , A   1, 01, 001 KH B   1, 01, 001 . Суматор 5 KH і a1  b1  1 . Нехай A 21  1 00, 001 і , БКН 7 (8) вибирається KH (табл. 2) виду (6) реалізує операцію (табл… 1, 2) A   1, 00, 001  1, 01, 001  0, 10, 000  B  KH B  1, 00, 000   1, 01, 001  0, 10, 000  . A 21  KH 21 Значення 0, 10, 100  і 0, 10, 000  з виходів відповідних суматорів 5 і 6 надходить на перші входи відповідно суматорів першої 9 і другої 10 груп. На другі входи суматорів 9 і 10 груп по шинам 11 надходять сигнали, що відповідають значенню констант ; 0, m1,2  m1,3  m1,,13  m1,14  m1 (тобто m1  j , для j  0, N  1 m1  2 ), таблиця 3. З виходів  5  n  10 суматорів 9 сформований ОК K 15A  K 15    1111011111 11111 (табл. 4) надходить на першу 10 15 20 n  10 групу входів СПОК 12. З виходів суматорів 10 ОК виду K15B  K15    1111011111 11111 (табл. 4) надходить на другу групу входів СПОК 12. Так як n A  nB  10 (табл. 5), тоді на першому n A  nB  виході СПОК 12 присутній вихідний сигнал, який через відкритий (табл. 6) ЕЗ 15 надходить до першого 16 виходу A  B пристрою. Це свідчить про те що A 21  B 21 . Таким чином, запропонована корисна модель для порівняння даних A  a1, a 2 ,, an  і B  b1, b 2 ,, bn  , що представлені у КЛ, дозволяє забезпечити достовірний результат порівняння. Даний ефект досягається за рахунок додаткового введення в пристрій-прототип третього елемента І, другого та третього елементів заборони, а також суматора за модулем два, шляхом використання модернізованого алгоритму порівняння двох чисел у непозиційній системі числення класу лишків. Даний ефект досягається при збереження всіх технічних характеристик пристрою-прототипу. ФОРМУЛА КОРИСНОЇ МОДЕЛІ 25 30 Пристрій для порівняння даних, що представлені у непозиційній системі числення класу лишків (КЛ), що містить перший і другий вхідні регістри, перший і другий блоки констант нулевізації, перший і другий суматори, першу і другу групи суматорів, схему порівняння однорядкового коду, перший і другий елементи І, перший і другий елементи АБО, перший елемент заборони, при цьому перший і другий входи пристрою підключено до входів відповідно першого та другого вхідних регістрів, виходи яких підключено до перших входів відповідно першого та другого суматорів, до других входів яких підключено виходи відповідно першого та другого блоків констант нулевізації, виходи першого та другого суматорів підключено до перших входів відповідно суматорів першої та другої груп, до других входів суматорів першої та другої груп підключені відповідні шини подачі констант виду 0,m1, 2  m1,, N  1  m1 ( N  n  m , де i mi i 2 35 40 45 50 модулі КЛ; n - кількість модулів КЛ; mi  mi1 ), а виходи суматорів першої та другої груп підключено відповідно до перших і других груп входів схеми порівняння однорядкового коду, перший nA  nB  вихід схеми порівняння однорядкового коду підключено до перших входів першого та другого елементів І та до першого (інформаційного) входу першого елемента заборони, вихід якого є першим A  B виходом пристрою, другий nA  nB  вихід схеми порівняння однорядкового коду підключено до першого входу першого елемента АБО, третій nA  nB  вихід схеми порівняння однорядкового коду підключено до першого входу другого елемента АБО, вихід підрегістра лишку a1 за найменшим модулем m1 КЛ першого регістра одночасно підключено до входу першого блока констант нулевізації та до другого входу першого елемента І, а вихід підрегістра лишку b1 за найменшим модулем m1 КЛ другого регістра одночасно підключено до входу другого блока констант нулевізації та до другого входу другого елемента І, а виходи першого та другого елементів І підключено до других входів відповідно першого та другого елементів АБО, який відрізняється тим, що введено суматор за модулем два, другий та третій елементи заборони, третій елемент І, при цьому вихід підрегістра лишку a1 за найменшим модулем m1 КЛ першого регістра підключено до першого входу третього елемента І та до першого входу суматора за модулем два, вихід якого підключено до другого (забороненого) входу першого елемента заборони, а вихід підрегістра лишку b1 за 8 UA 79587 U 5 найменшим модулем m1 КЛ другого регістра підключено до другого входу третього елемента І та до другого входу суматора за модулем два, виходи першого та другого елементів АБО підключено до перших (інформаційних) входів відповідно другого та третього елементів заборони, вихід третього елемента І підключено до других (заборонених) входів відповідно другого та третього елементів заборони, виходи яких є відповідно другим A  B і третім A  B виходами пристрою. Комп’ютерна верстка Л. Литвиненко Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601 9