Система кутової стабілізації космічних апаратів

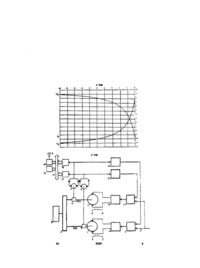
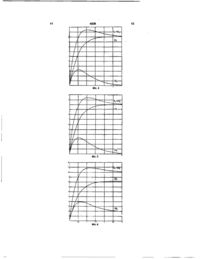
Система кутової стабілізації космічних апаратів, що містить послідовно з'єднані електропривід, редуктор і маховик, яка відрізняється тим, що вона оснащена другим електроприводом, другим редуктором, причому виходи першого та другого редукторів підключені до першого та другого входів диференціала, вихід якого з'єднаний з маховиком, вихід першого редуктора через перший вимі рювач кутової швидкості першого електропривода та перший масштабний перетворювач з'єднаний з другим входом другого суматора, вихід якого з'єднаний з входом другого підсилювача, вихід якого з'єднаний з входом другого електропривода, вихід другого редуктора через другий вимірювач кутової швидкості другого електропривода і другого масштабного перетворювача з'єднаний з другим входом першого суматора, вихід якого з'єднаний з входом першого підсилювача, вихід якого з'єднаний з входом першого електропривода, перші входи першого і другого суматорів з'єднані і створюють керуючий вхід системи кутової стабілізації космічних апаратів, виходи першого і другого вимірювачів кутової швидкості першого та другого електропривода з'єднані з входом мікропроцесора. Корисна модель відноситься до галузі космонавтики і може бути використаний для системи кутової стабілізації космічних апаратів (КА) у яких в якості виконавчих органів використовуються тіла обертання. Відома системи кутової стабілізації (КА) з використанням в якості виконавчих органів двигунів маховиків (ДМ) [1]. Недоліками відомої системи є те, що інерційний момент створений таким маховиком залежить від маси використаного маховика. Відома системи кутової стабілізації (КА) з використанням електроприводу [2]. Відома система має наступні недоліки. Перший недолік пов'язаний з нелінійним характером зміни інерції маховика, причому, в процесі наростання кутової швидкості електропривода прискорення зменшується від максимуму до нуля. Другий недолік пов'язаний з коротким проміжком часу існування керуючого моменту за рахунок режиму насичення. Третій недолік пов'язаний з впливом на точність формування керуючого моменту параметричних збурювань передаточної функції електроприводу. Четвертий недолік пов'язаний зі скороченим ресурсом електропривода, так як при його відмові об'єкт стає некерованим. Відома системи кутової стабілізації (КА) з використанням маховиків зі змінним моментом інерції [3], що складається з одного ДВ, редуктора та маховика є прототипом. Недоліками таких систем є складність реалізації механізмів дозволяючих зробити розкриття маховика, знижена точність реалізації необхідного закону та мають низький ресурс використання обумовлений відмовою спрацьованістю одного електропривода (ЕП). В основу корисної моделі поставлено задачу удосконалити систему кутової стабілізації (КА) шляхом підвищення точності реалізації лінійного закону керування, забезпечення інваріантності передаточної функції ЕП від параметричних збурювань, підвищення ресурсу системи кутової стабілізації КА, що забезпечує досконалість технічного рішення. Поставлена задача вирішується тим, що в системи кутової стабілізації КА, яка містить послідовно з'єднані ЕП, редуктор і маховик, новим є те, що система отримує другий ЕП, другий редуктор, причому виходи першого та другого редукторів, підключені до першого та другого входам дифере (24)17.01.2005 СО CM in о> 4526 нціала, вихід якого з'єднаний з маховиком, вихід першого редуктора через перший вимірювач кутової швидкості першого ЕП та перший масштабний перетворювач (МИ) з'єднаний з другим входом другого суматора, вихід якого з'єднаний з входом другого підсилювача, вихід якого з'єднаний з входом другого ЕП, вихід другого редуктора через другий вимірювач кутової швидкості другого ЕП і другого МП з'єднаний з другим входом першого суматора, вихід якого з'єднаний з входом першого підсилювача, вихід якого з'єднаний з входом першого ЕП, перші входи першого і другого суматорів з'єднані і створюють керуючий вхід системи кутової стабілізації КА, виходи першого і другого вимірювачів кутової швидкості першого та другого ЕП з'єднані з входом мікропроцесора. На Фіг.1 представлена кінематична схема кутової стабілізації КА в трьохмірному просторі по осям X Y Z. На Фіг.2 представлена принципова схема системи кутової стабілізації КА по одній вісі орієнтації. Фіг.З ілюструє властивість інваріантності результуючого коефіцієнту передачі одною канала стабілізації від параметричних збурювань другою каналу. Фіг.4-5 представлені перехідні процеси в системі при формуванні кінетичного моменту керування. Фіг.6-7 представлені перехідні процеси в системі при параметричних збуреннях статичних коефіцієнтів в діапазоні +/- 20%. Системи кутової стабілізації КА, у відповідності до запропонованого технічною рішення складається з першого і другого ЕП 1 і 2, першого і другого редукторів 3 і 4, першого і другого вимірювачів кутової швидкості (ТГ) 5 і 6, диференціала 7, маховика 8, першого і другого суматорів 9 і 10, першого і другого підсилювачів 11 і 12, першого і другого МП 13 і 14, модулів вводу аналогових сигналів (АЦП) 15, 16, інтерфейс 17, мікропроцесор 18, модуль виводу цифрових сигналів (ЦАП) 19. Причому, вихід першого ТГ 5 після першого МП 13 підключений до 2-го входу 2-го суматора 10, а вихід 2-го ТГ 6 після другого МП 14 підключений до 2-го входу 1-го суматора 9, а перші входи 1-го і 2го суматорів 9 і 10 поєднані і створюють вхід приладу. Елементи 9, 11, 1 і 3 створюють перший канал формування керуючого моменту. Елементи 10, 12, 2 і 4 створюють другий канал формування керуючого моменту. Системи кутової стабілізації КА функціонує наступним чином. Нехай передаточні функції 1-го і 2-го ЕП 1 і 2, з приведеним моментом інерції маховика до входу ЕП мають наступний вигляд: =T= де є - сигнал задания; юі і а 2 - відповідно куто> ві швидкості 1-го і 2-го ЕП; К-і і К2 - передаточні коефіцієнти 1-го і 2-го каналів; аі і аг - коефіцієнти характеризуючі постійні часу 1-го і 2-го ЕП. У відповідності з запропонованим способом кутова швидкість 1-го ЕП сої перетворюється в 4 сигнал Ui 1-го ТГ5, масштабується в МП 13 і алгебраїчно сумується в другому суматорі 10 з сигналом задания і формується сигнал управління 2-м ЕП 2 у відповідності з рівнянням U2=e-PiUi (3) де U-FKfl/icol, U 2 - сигнал на вході 2-го підсилювача 12; є - сигнал задания; Ui - сигнал на виході ТГ5; Рі - коефіцієнт передачі МП 12; К№1 - коефіцієнт передачі ТГ5. Далі, кутова швидкість 2-го ЕП 2 со2 перетворюється в сигнал U 2 2-го ТГ6, масштабується в МП 14 і алгебраїчно сумується в 1-му суматорі 9 з сигналом задания і формується сигнал управління 1м ЕП 1 у відповідності з рівнянням Ui=e+p 2 U 2 (4) де Ui - сигнал на вході 1-го підсилювача 11; 112=^0)2 - сигнал на виході ТГ6; рг - коефіцієнт передачі МП 13; К^ - коефіцієнт передачі ТГб. На основі рівнянь (1) - (4) можна скласти наступну систему (Di(s)=Wi(s)8+W2(s)p2a)2(s) (5) a>2(s)=W2(s)e-Wi(s)Picoi(s) (6) Рівняння (5) - (6) можна представити в наступному вигляді o)1(s)-W2(s)Pico2(s)=Wi(s)e (7) Ms)+Wi(s)p 2 coi(s)=W 2 (s) e (8) Рівняння (7) - (8) можна представши в матричній формі 1 W(s) r p 2 -W(s)2-Pi^| Ґю^-Л fW(s).) 1 J|co(s)2J = lw(s) 2 (9) Розв'язком системи (9) буде система 2-х параметрично взаємозалежних рівнянь (1 +Wi (s) W 2 (s)pi р2)юі (s)=Wi (s)(1 +W2(s)p2)e (10) (1+Wi(s)W2(s)p1p2)o)1(s)=W2(s)(1-W1(s)pi)e (11) З урахуванням передаточних функцій (1), (2) отримаємо (s) = (12) а1 • а 2 • s 2 + (а., + а 2 ) • s +1 + К-, • К 2 • р г р 2 ю 2 • (s) = (13) Таким чином, в результаті, взаємозалежних і цілеспрямованих дій, виконуючих над математичними об'єктами, першим з яких являється 1-й ЕП 1, а другим - 2-й ЕП 2, створені дві структури, функціонально визначені рівняннями (12) - (13). Подібні рівняння визначають рефлексивну взаємодію, бо перший об'єкт за допомогою рефлексивних зв'язків 5-13, взаємодіє з другим об'єктом, а другий об'єкт, в свою чергу, за допомогою рефлексивних зв'язків 5-13, взаємодіє з першим об'єктом. При виконанні умови: КіРі=1, (14) що досить просто досягається вибором коефіцієнта МП 5 Рі=1/Кі система (12) і (13) зводиться до вигляду. 4526 (1 + K 2 p 2 ) a2 (15) 00(8)! = • 2 a 2 s + (a 1 +a 2 ) s + 1 + K 2 p 2 K 2 a^ s (16) CO(S)2 = a 2 s +(a-!+a 2 ) s + 1 + K 2 p 2 Рівняння (15) - (16) зводяться до стандартного вигляду co(s)2 = \ s + b0 (17) С 2 s^+C, S + 1 b2 s 2 Co S + d S + 1 С = 1 1 + К2 р2 2 1 + K2 p 2 Статична передаточна функція при цьому буде мати наступний вигляд А-,= (18) , р, к 2 р 2 - передаточна функція 1 -го канапу К А2= 2(1-К1Р1) 2 1 + К І р, К 2 р 2 - передаточна функція 2-го каналу ДЄ 1 1 + K2 p 2 , р, к 2 р2 К ^ (21) - результуючий коефіцієнт передачі системи Для отримання залежностей (19) - (21), задамося наступними розрахунковими значеннями Кі=К2=10, рі=0,1,р2=0,5 Результати розрахунків наведені в таблиці 1 і показані на Фіг З Таблиця 1 Кі Аі А2 А 0 0 10 10 2 6 4 10 4 8 2 10 6 9 1 10 8 9,6 0,4 10 10 10 0 10 З таблиці 1 очевидно, що результуючий коефіцієнт передачі системи А інваріантен відносно параметричних збурень коефіцієнта прямого перетворення Кі 1 -го каналу Це відбувається тому, що при зменшені коефіцієнта Кі на величину ЛКі коефіцієнт Аі зменшується на величину ААі При цьому, коефіцієнт А2 збільшується на величину АА2, причому ААі=ДА2 внаслідок чого результуючий коефіцієнт передачі системи залишається незмінним A=const Ця властивість рефлексивних систем відносить їх до класу самоорганізаційних Покажемо, що абсолютна похибка результуючого коефіцієнта передачі запропонованого способу менше, ніж в одноканальній схемі (прототипу) при одночасному параметричному збуренні коефіцієнтів передачі Кі і К2 Нехай Кі=К2=8 Тоді А І = 9 , 5 2 3 , А 2 =0,381, А=9,904, а абсолютна похибка коефіцієнта передачі системи буде А А = 1 ° - 9 0 9 0 4 1 0 0 % = 0,9% Таким чином, при похибці обох каналів на 20% загальний коефіцієнт передачі зменшиться лише на 0,9% Причому, система залишається працездатною навіть при "ВІДМОВІ" ОДНОГО З ЕП Для побудови перехідних процесів, ВІДПОВІДНИХ передаточним функціям (17) і (18), приведемо розрахунковий приклад Задамося наступними параметрами системи K1=K2=10, /Зі=0,1, р2=0,01, аі=0,5, а2=0,6 12 10,285 -0,285 10 14 10,5 -0,5 10 16 10,666 -0,666 10 18 10,8 -0,8 10 20 10,9 -0,9 10 6s + 10 41 916 31,916 (19) 2s + 1 1666s + 1 0,3s + 1,1s+ 1 5s 14 97 14,97 (20) W(s) 2 = 2 0,3s + 1,1s+ 1 1666S + 1 2s+ 1 W(s)1 = 2 Тоді рівняння (17) і (18) будуть мати наступний вигляд Передаточним функціям (19) і (20) будуть відповідати наступні рівняння перехідних процесів Перехідні процеси ВІДПОВІДНІ цим рівнянням отримані на комп'ютері та приведені на Фіг 4-7 Аналіз сумарного перехідного процесу на виході диференціального механізму 7, Фіг 2, кінетичний момент якого прикладений до маховика, показує, co(t)i=10+31,916e 075t -41,916e 0S0t w(t) 2 =14,97(e 2t -e 1666t ) co(t)E=10+31,916(e075-1,313e050t)+14,97(e2t-e 1666t ) що він підпорядковується лише в певному діапазоні (проміжок часу лінійного закону), у ВІДПОВІДНОСТІ з рівнянням co(t)z=Kt=115t де K=tga - кут нахилу часової характеристики по відношенню до ВІСІ часу Дійсно це можна відобразити даними, викладеними в таблиці 2 4526 Таблиця 2 t cos(t) 0,02 2,3 0,04 4,6 Наявність лінійної залежності, в певному проміжку часу, сумарної кутової швидкості від часу, свідчить про постійний кут нахилу вектора кутової швидкості до осі часу, що приводить до кінетичного моменту, прикладеного до КА. Це важлива властивість системи Фіг.2, так як спрощує використання моменту маховика в системі керування (СК) КА. При оберіганні маховика безперервно змінюються кутові швидкості сої і юг першого і другого ЕП шляхом вводу сигналів з тахогенератора 5 і 6 в мікропроцесор і розв'язання рівнянь coi=K 5 U 5 де Us і ІІб - сигнали тахогенераторів 5 і 6; Ks і Кє - коефіцієнти пропорційності. Отримане значення кутової швидкості ooz порівнюються з заданим значенням соз і в момент їх рівності формується сигнал в систему кутової стабілізації на скидання кінетичного моменту шляхом включення реактивних двигунів КА. На Фіг.8 представлені перехідні процеси в сис Фіг. 1 0,06 6,9 0,08 9,2 0,1 10,15 темі коли коефіцієнт Кі зменшився на 20% тобто Кі=8. Тоді, перехідний процес в 1-му каналі прямує до статичного значення Ні=8, а в 2-му каналі до статичного значення Нг=2. Це означає, що сумарний перехідний процес залишається незмінним, Н=10. На Фіг.9 представлені перехідні процеси в системі при Кі=12. Представлені розрахунки доводять переваги запропонованого способу в порівнянні з прототипом, що полягає в підвищені надійності, швидкодії і інваріантності сумарного коефіцієнту передачі від параметричних збурювань окремих каналів. Література: 1. Космические аппараты. Под общей ред. К.П. Феоктистова. М., Воениздат, 1983, стр. 240; 2. Системы угловой стабилизации космических аппаратов. М., Машиностроение, 1980 стр. 48; 3. Каргу Л.И. Системы угловой стабилизации космических аппаратов. М., Машиностроение, 1980 стр. 68-71. &t xo* 91 Ч! Н 11 4526 -ь н Фіг. 4 Фіг. 5 13 Комп'ютерна верстка А Крулевский 4526 Підписне 14 Тираж 37 прим Міністерство освіти і науки України Державний департамент інтелектуальної власності, вул Урицького, 45, м Київ, МСП, 03680, Україна ДП "Український інститут промислової власності", вул Глазунова, 1, м Київ - 42, 01601