Спосіб навчання стохастичної нейронної мережі

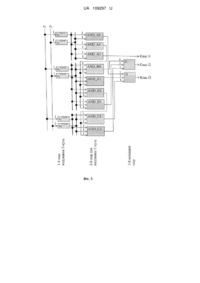
Реферат: UA 109297 U UA 109297 U 5 10 15 20 25 30 35 40 45 50 55 60 Корисна модель належить до нейрокібернетики і може бути використана у нейрокомп'ютерах та штучних стохастичних нейронних мережах для класифікації заданого на вході випадкового вхідного вектора невідомого класу X = (х1, х2,…, хj, …, хn), де j=1, 2,…, n порядковий номер змінної xj. Хоча функціонування подібних мереж є детермінованим і використовується незмінна вибірка для їх навчання, але вони звуться стохастичними, бо призначені для класифікації стохастичних векторів невідомого класу, а вибірка для навчання є репрезентативною і складається з випадкових векторів [1; 2, с. 218]. Відомий спосіб навчання стохастичної нейронної мережі, за яким класифікують вхідний стохастичний вектор невідомого класу X = (х1, х2,…, xj, …, хn), де j=1, 2,…, n - порядковий номер числової змінної xj вектора X, на основі початкової навчальної вибірки стохастичних векторів δ,е δ,е δ,е δ,е δ,е Х = (x1 , х2 , …, xj , …, хn ) з розділювальними обмеженнями, під якими розуміють групи δ,е векторів Х у вигляді їх кластерів у вибірці, де δ = 1, 2,…, q - порядковий номер кластера, j=1, δ,е δ,е 2,…, n - порядковий номер числової змінної хj навчального вектора X , e=1, 2,…, Е δ,е порядковий номер навчального вектора X у навчальній вибірці, при якому невідомий вектор X класифікують по найбільшій схожості до вектора-центроїда кластера [3, с. 153]. Недоліками даного способу навчання стохастичної нейронної мережі є зменшення точності δ,е класифікації векторів невідомого класу X при змішаному розміщенні навчальних векторів Х різних класів, хоча з точки зору спрощення розрахунків і економії часу цей спосіб навчання є найбільш ефективним для нейронних мереж з чітко розділеними кластерами. Відомий спосіб навчання стохастичної нейронної мережі, за яким класифікують вхідний стохастичний вектор невідомого класу X=(х1, х2,…, xj, …, хn), де j=1, 2,…, n - порядковий номер числової змінної xj вектора X, на основі початкової навчальної вибірки стохастичних векторів k,е k,е k,е k,е k,е Х = (х1 , х2 ,…, xj ,…, хn ) з розділювальними обмеженнями, під якими розуміють заборону k,е мати у навчальній вибірці чи у її групі вектори X з різними класами, заборонені відстані між k,е векторами Х , заборонені стохастичні показники вибірки чи її групи та ін., k=1 - тип навчальної k,е k,е вибірки векторів X чи окремих навчальних груп вибірки з векторами X , серед яких присутні k,е розділювальні обмеження, j=1, 2,…, n - порядковий номер числової змінної xj навчального k,е k,е вектора Х , e=1, 2,…, Е - порядковий номер навчального вектора Х у навчальній вибірці, при якому розділювальним обмеженням є "близькість сусіда", і клас невідомого вектора X k,е визначають по класу "найближчого сусіда" - вектора Х з найбільшою схожістю до вектора X [3, с. 153]. Недоліками даного способу навчання є збільшення витрат на стохастичну нейронну мережу та її обслуговування через збереження в нейронній мережі великої кількості інформації вибірки та недостатня точність класифікації вхідного вектора X внаслідок не урахування густини розподілу сусідніх векторів. Найбільш близьким до заявленого способу навчання стохастичної нейронної мережі є вибраний за прототип спосіб навчання, за яким класифікують вхідний стохастичний вектор невідомого класу X = (х1, х2,…, xj, …, xn), де j=1, 2,…, n - порядковий номер числової змінної xj k,е k,е k,е вектора X, на основі початкової навчальної вибірки стохастичних векторів Х = (хі , х2 ,…, k,е k,е k, е xj ,…, хn ), де k=0 - тип навчальної вибірки векторів Х чи окремих навчальних груп вибірки з k, е векторами Х , серед яких відсутні вектори різних класів чи вектори з іншими розділювальними обмеженнями, під якими також розуміють заборону мати у навчальній вибірці чи у її групі k,е k,е вектори X із забороненими відстанями між векторами Х або із забороненими стохастичними k,е показниками вибірки чи її групи та ін., k=1 - тип навчальної вибірки векторів Х чи окремих k,е навчальних груп вибірки з векторами Х , серед векторів яких присутні розділювальні k,е k,е обмеження, j=1, 2,…, n - порядковий номер числової змінної xj навчального вектора Х , е= k,е 1,2,…, Е - порядковий номер навчального вектора X у навчальній вибірці, згідно з яким змінні k,е k,е xj кожного вхідного навчального вектора X використовують як вагові коефіцієнти п входів кожного відповідного нейрона групи у шарі зразків, кожному нейрону шару зразків привласнюють функцію (Гаусса), позитивне числове значення якої збільшується до 1 при k,е співпаданні координат векторів X та X всі виходи групи нейронів одного класу шару зразків з'єднують з входами відповідного нейрона-суматора даного класу у підсумовуючому шарі, по максимальному значенню виходу нейрона-суматора відповідного класу визначають клас вхідного вектора X [1]. Даний спосіб навчання є аналогом байєсового класифікатора, за яким вхідний невідомий стохастичний вектор X = (х1, x2,…, xn) класифікують за допомогою центроїдів кластерів (класів) δ δ δ по найбільшій величині байєсового класифікатора А Р f , де δ = 1,2,…, q - порядковий номер δ кластера (класу), А - витрати внаслідок заперечення наявності δ-го кластера (класу) при його δ реальній присутності; Р - апріорна ймовірність появи 8-го кластера (класу), яку або визначають по опублікованим даним, або приймають рівною відношенню кількості векторів δ-го класу в 1 UA 109297 U 5 10 15 20 25 30 35 40 45 50 55 60 початковій навчальній вибірці до загальної кількості навчальних векторів Е в початковій вибірці; f - оцінка функції густини ймовірності -го кластера (класу) [2, с. 219-221; 3, с. 154]. Причини, які перешкоджають одержанню очікуваного технічного результату у прототипі (зменшення кількості нейронів, зменшення часу класифікації, спрощення розрахунків) є прийнятий алгоритм роботи та архітектура нейронної мережі. Недоліками прийнятого за прототип способу навчання є збільшення витрат на стохастичну нейронну мережу та її обслуговування через збільшення кількості нейронів в нейронній мережі та ускладнення розрахунків. Технічним результатом пропонованої корисної моделі є зменшення витрат на стохастичну нейронну мережу та її обслуговування через зменшення загальної кількості нейронів в нейронній мережі і спрощення розрахунків. Згідно з пропонованим способом проводиться по суті не навчання нейронної мережі, а групування всієї сукупності навчальних стохастичних векторів по заздалегідь визначених тілесних кутах, які упорядковано "географічно" розміщені в гіперсфері і у які попадають кінцеві точки навчальних векторів. Загальні суттєві ознаки запропонованого способу навчання стохастичної нейронної мережі, які співпадають з суттєвими ознаками прототипу, полягають у тому, що вхідний стохастичний вектор невідомого класу X=(х1, x2,…, xj, …, xn), де j=1, 2,…, n - порядковий номер числової k,е k,е змінної xj вектора X, на основі початкової навчальної вибірки стохастичних векторів Х = (хі , k,е k,е k,е k,е х2 ,…, xj ,…, хn ), де k=0 - тип навчальної вибірки векторів X чи окремих навчальних груп k,е вибірки з векторами X , серед яких відсутні вектори різних класів чи вектори з іншими розділювальними обмеженнями, під якими також розуміють заборону мати у навчальній вибірці k,е k,е чи у її групі вектори Х із забороненими відстанями між векторами X або із забороненими k,е стохастичними показниками вибірки чи її групи та ін., k=1 - тип навчальної вибірки векторів Х k,е чи окремих навчальних груп вибірки з векторами X , серед векторів яких присутні k,е розділювальні обмеження, j=1, 2,…, n - порядковий номер числової змінної xj навчального k,е k,е вектора Х , e=1, 2,…, Е - порядковий номер навчального вектора Х у навчальній вибірці. Суттєві ознаки запропонованого способу навчання нейронної мережі, що є достатніми у всіх випадках і характеризують запропонована корисна модель на відміну від прототипу, полягають у тому, що на етапі навчання будують нейронну мережу на основі використання навчальної k,е вибірки з векторами Х , для чого вагові коефіцієнти входів всіх нейронів нейронної мережі прирівнюють 1 і не змінюють, нейронній мережі надають обов'язкові 1-й і 2-й шари нейронів та необов'язковий 3-й шар нейронів, з яких 1-й та 2-й шари нейронів можуть мати ряд паралельних ієрархічних аналогічних шарів нейронів, кожному з яких призначають індивідуальну вибірку навчальних векторів та визначають на основі даних цієї індивідуальної вибірки відповідний λ λ λ λ λ центр координат X - (х1 , х2 …, хj …, хn ), де λ - 1, 2, 3, … - порядковий номер ієрархії, у 1-му шарі на етапі навчання для вищого першого ієрархічного рівня λ = 1 призначають як індивідуальну вибірку початкову навчальну вибірку, для цієї вибірки визначають центр λ=1 λ=1 λ=1… λ=1 λ=1 λ=1 координат X - (х1 , х2 , хj …, хn ), у якому значення координат xj прирівнюють нулю λ=1 k,е k,е (xj =0), якщо навчальні вектори Х вибірки вміщують змінні xj з різними знаками при λ=1 однакових нижніх індексах j, а у іншому разі елементи центра координат X прирівнюють координатам серединної точки початкової вибірки у вигляді, наприклад, координат кінцевої точки вектора центроїда відповідних векторів або точки "центру тяжіння" відповідного Т-кута k,е типу k=1, перераховують координати навчальних векторів Х початкової навчальної вибірки на λ k,e,λ=1 координати навчальних векторів для нового центра координат X у вигляді векторів X k,e,λ=1 k,e,λ=1 k,e,λ=1 k,e,λ=1 k,e.λ=1 k,е, =1 (х1 , х2 …, хj …, хn )], де xj = (xj -xj ), у 1-й шар вводять n нейронів першого ієрархічного рівня λ = 1, кожний з яких має один вхід, що з'єднують на етапі навчання з k, e,λ=1 k,e,=1 числовою змінною хj вхідного навчального вектора X індивідуальної навчальної C,λ=1 вибірки, і має один вихід, на якому отримують для j-ro нейрона або код xj =0, якщо знак k,е,λ=1 C,λ=1 C,λ=1 =1 різниці (xj xj ) є від'ємним, або у іншому разі - код xj =1, а сукупність виходів X C,λ=1 C,λ=1 C,λ=1 C,λ=1 (х1 , х2 …, хj …, хn ) всіх n нейронів 1-го шару у першому ієрархічному рівні λ = 1 розглядають як розряди двійкового числа і вважають сукупність значень цих розрядів порядковим номером у двійковій системі числення відповідного Т-кута типу k=0 або k=1, у 2-й шар першого ієрархічного рівня λ = 1 вводять нейрони типу T_AND_0, кількість яких дорівнює загальній кількості Т-кутів типів k=0 та k=1 початкової навчальної вибірки з навчальними k,e,λ=1 векторами X першого ієрархічного рівня λ = 1, для кожного нейрона типу T_AND_0 вводять n входів, які з'єднують з відповідними п виходами нейронів 1-го шару першого ієрархічного рівня λ = 1, кожному нейрона типу T_AND_0 призначають для розпізнавання індивідуальний порядковий двійковий номер Т-кута, рівний одному з порядкових двійкових номерів Т-кутів k,e,λ=1 початкової вибірки з навчальними векторами X , якщо частка початкової навчальної вибірки k,e,λ=1 k,e,λ=1 векторів X розміщена в T-куті типу k=0, який охоплює всі навчальні вектори X даного 2 UA 109297 U 5 10 15 20 25 30 35 40 45 50 55 класу, то на виході відповідного нейрона Т_AND_0 для Т-кута типу k=0 отримують вихідний сигнал відповідного класу стохастичної нейронної мережі, якщо частка початкової навчальної k,e,=1 вибірки векторів X розміщена в Т-куті типу k=0, який охоплює лише частку навчальних k,e,=1 векторів X даного класу, то вихід відповідного нейрона Т_AND_0 для Т-кута типу k=0 з'єднують з входом відповідного нейрона-суматора 3-го шару нейронів, на виході якого отримують вихідний сигнал для одного з відповідних класів нейронної мережі, і вводять для цього нейрона-суматора 3-го шару нейронів кількість входів, яка дорівнює кількості Т-кутів типу k,e,=1 k=0, у які попали навчальні вектори X даного одного класу, якщо частка початкової k,e,=1 навчальної вибірки векторів X розміщена в Т-куті типу k=1, то всі належні даному Т-куту k,e,=1 типу k=1 навчальні вектори X різних класів розглядають як окрему скорочену стохастичну навчальну вибірку нижчої ієрархії, яка потребує подальшого розділу на частки з використанням способу навчання нейронної мережі, аналогічного описаному вище, сигнал виходу нейрону T_AND_0 для Т-кута типу k=1 розглядають як сигнал дозволу на вихід відповідного сигналу нижчої ієрархії, вихід цього нейрона T_AND_0 з'єднують з додатковим (n+1) -м входом до ієрархічно нижчого нейрона T_AND_0 для Т-кутів типу k=0 та k=1 при ієрархічних рівнях λ > 1, для чого в нейронну мережу у 1-му та 2-му шарах при ієрархічних рівнях λ > 1 вводять нові ієрархічно нижчі рівні із загальною кількістю ієрархічно нижчих шарів, яка дорівнює кількості наявних у вищому ієрархічному рівні Т-кутів типу k=1, а кожний з ієрархічно нижчих рівнів має у 1-му та 2-му шарі структуру та зв'язки, аналогічні описаним вище для вищого ієрархічного рівня λ = 1, за винятком того, що кожний ієрархічно нижчий рівень при λ > 1 має індивідуальний λ визначений для даної скороченої вибірки центр координат X , а кожний з відповідних нейронів T_AND_0 2-го шару нижчих ієрархічних рівнів має додатковий (n+1)-й вхід, який з'єднують з виходом відповідного нейрона T_AND_0 попереднього вищого ієрархічного рівня, що вміщує k,e, групу відповідних навчальних векторів X типу k=1 нижчого рівня, з наступним повторним дробленням ієрархічно нижчих скорочених вибірок навчальних векторів Т-кутів типу k=1 до k,e,=1 охоплення всіх векторів X вищого ієрархічного рівня λ= 1 всіма вихідними сигналами Т-кутів типу k=0 з 2-го та 3-го шарів, по яких визначають клас вхідного вектора X, а на етапі використання нейронної мережі на всі ієрархічні входи всіх ієрархічних рівнів λ 1-го шару подають вхідний стохастичний вектор невідомого класу X, на виходах всіх ієрархічних шарів 1λ го шару отримують виходи результатів кодування різниць (xj-xj ) у вигляді двійкових порядкових C,λ номерів X відповідних Т-кутів типу k=0 або k=1, у які може попасти вхідний вектор невідомого класу X, у 2-му шарі вмикають на подальше дроблення скорочені вибірки навчальних векторів Т-кутів типу k=1 на ієрархічно нижчих рівнях 1 -го та 2-го шарів, нейрони 2-го шару типу T_AND_0 по отриманому Т-куту типу k=0 класифікують вхідний вектор X, а у 3-му шарі, який не є обов'язковим, об'єднують на нейронах-суматорах сигнали з 2-го шару від виходів нейронів типу T_AND_0, що розпізнають індивідуальні номери Т-кутів типу k=0 однакових класів. Передбачуваний спосіб навчання стохастичної нейронної мережі ілюструється кресленнями, на яких наведено: Фіг. 1 - гіпершар радіусом Rm з тілесним кутом; Фіг. 2 - порядкові номери з тілесних кутів у десятковій системі числення; Фіг. 3 - структурна схема нейрона T_AND_0 [4]; Фіг. 4 - розміщення навчальних векторів у двовимірній системі координат; Фіг. 5 - стохастична нейронна мережа. На Фіг. 1 позначено: - R - радіус гіпершару; - S - площа на гіперсфері шару, яку перетинають промені (напрямки векторів) усіх векторів тілесного кута n-мірного гіпершару, що виходять з центру гіпершару. На Фіг. 2 позначено: - х1, х2 - осі координат двомірного простору. В тексті заяви замість слів "простір", "круг", "коло" використовуються відповідні слова "гіперпростір", "гіперкуля", "гіперсфера", щоб підкреслити, що ми розглядаємо загальний випадок гіперпростору (поняття якого не змінюються у залежності від кількості осей), але вони мають перероджений вигляд у двовимірній (і одновимірній) системі координат; - g=0, g=1, g=2, g=3 - порядкові номери Т-кутів в десятковій системі числення. На Фіг. 3 позначені вихідна змінна та вхідні змінні нейрона "T_AND_0", який виконує складну логічну функцію [4]: α α - хj , j=1, 2,…,n - вхідні змінні, які всі повинні мати призначені їм значення "1" для отримання виходу у = 1 нейрона "T_AND_0"; α α - j=1, 2,…, n - порядкові номери вхідних змінних xj нейрона "T_AND_0"; 3 UA 109297 U β 5 10 15 20 25 30 35 40 45 50 55 60 α α - xj , j=n + 1, n + 2,…,n - вхідні змінні, які всі повинні мати призначені їм значення "0" для отримання виходу у = 1 нейрона "T_AND_0"; α α β - j=n + 1, n + 2,…, n - порядкові номери вхідних змінних xj нейрона "T_AND_0"; β - у - вихід нейрона "T_AND_0", який дорівнює 1, якщо значення всіх входів "xj = 0" та всіх α входів "xj = 1" дотримуються сумісно; в іншому разі вихід у=0. На Фіг. 4 позначено: - x1, x2 - позначення осей початкової системи координат, яка помічена літерою А. Пунктиром наведені позначені літерами В та С нові системи координат для ієрархічно нижчих і менших за розмірами Т-кутів навчальних векторів без позначення їх осей, бо вони співпадають з позначеннями і напрямками наведених осей (х1, х2), позначеними літерою А; - g=0, g=1, g=2, g=3 - порядкові номери Т-кутів в десятковій системі числення (виділені у прямокутниках із сірим фоном) для початкової системи координат, яка позначена літерою А. Ці порядкові номери є вірними й для систем координат, поміченими літерами В та С; i.e - e=1, 2, З, 4, 5 - помічені цифрами кінцеві точки навчальних векторів Х класу і = 1 (позначені чорними колами); i.e - e=6, 7, 8 - помічені цифрами кінцеві точки навчальних векторів Х класу і = 2 (позначені чорними ромбами); i.e - e=9, 10, 11, 12, 13, 14, 15 - помічені цифрами кінцеві точки навчальних векторів Х класу і = 3 (позначені прямокутниками); - X - позначена чорним трикутником точка, яка відображує координати (х 1, x2) вхідного вектора X невідомого класу. На Фіг. 5 позначено: - 1 - вагові коефіцієнти входів нейронів, які не змінюються у процесі навчання нейронної мережі; C,λ=1 C,λ=1 x1 , x2 - нейрони "1-го шару кодування Т-кута" нейронної мережі, які складають вищий C,=1 ієрархічний рівень (λ = 1) у 1-му шарі нейронної мережі, вихідні сигнали яких помічаються x1 , C,=1 x2 (по позначенню нейронів); C,=2 C,=2 - x1 , x2 - нейрони "1-го шару кодування Т-кута" нейронної мережі, які складають другий ієрархічний рівень (λ = 2) у 1-му шарі нейронної мережі, вихідні сигнали яких C,=2 C,=2 помічаються x1 , x2 - (по позначенню нейронів); C,=3 C,=3 - x1 , x2 - нейрони "1-го шару кодування Т-кута" нейронної мережі, які складають третій C,=3 ієрархічний рівень (λ = 3) у 1-му шарі нейронної мережі, вихідні сигнали яких помічаються x1 , C,=3 x2 (по позначенню нейронів); - AND_AO, AND_A1, AND_A3 - нейрони типу "T_AND_0" [4]. Вихідні сигнали нейронів помічаються по їх позначенню. Кінцеві частки позначень у вигляді "А0", "А1", "A3" означають: літера "А" - позначення системи осей координат на Фіг. 4; кінцеві цифри 0, 1,3- порядкові номери Т-кутів у десятковій системі числення g у вказаній системі координат А на Фіг. 4; - AND_B0, AND_B1, AND_B2, AND_B3 - нейрони типу "T_AND_0" [4]. Вихідні сигнали нейронів помічаються по їх позначенню. Кінцеві частки позначень у вигляді "ВО", "В1", "В2", "В3" означають: літера "В" - позначення системи осей координат на Фіг. 4; кінцеві цифри 0, 1, 2, 3 порядкові номери Т-кутів у десятковій системі числення g у вказаній системі координат В на Фіг. 4; - AND_C1, AND_C2 - нейрони типу "T_AND_0" [4]. Вихідні сигнали нейронів помічаються по їх позначенню. Кінцеві частки позначень у вигляді "С1", "С2" означають: літера "С" - позначення системи осей координат на Фіг. 4; кінцеві цифри 1, 2 - порядкові номери Т-кутів у десятковій системі числення g у вказаній системі координат С на Фіг. 4; - i2, i3 - нейрони-суматори 3-го шару нейронів, на виході кожного з яких отримують вихідний сигнал для одного з відповідних класів нейронної мережі; - Клас і1, Клас i2, Клас i3 - виходи нейронної мережі, на одному з яких сигнал 0 замінюється на сигнал 1, якщо вхідний стохастичний вектор X = (х1, х2,…, xj, …, хn) належить до відповідного класу; - 1-й шар кодування Т-кута, 2-й шар для виділення Т-кута, 3-й вихідний шар - шари нейронної мережі, кожний з яких складається з визначеної кількості нейронів. Спочатку розглянемо деякі визначення, які використовуються нижче при описі способу навчання стохастичної нейронної мережі. Нижче у n-вимірному гіпероб'ємі, поряд з поняттям кластера [2, 3, 5-8] як підмножини найбільш схожих навчальних векторів з числовими змінними та з визначенням для кластера типового представника (центроїда - як вектора із середніми значеннями координат навчальних векторів, що складають кластер), також використовується більш широке поняття тілесного кута (Т-кута). Т-кутом n-вимірного гіпероб'єму зветься його частина, яка об'єднує усі вектори, промені 4 UA 109297 U 5 10 15 20 25 30 35 40 45 50 55 60 яких (напрямки векторів) виходять з центру координат і перетинають деяку гіперповерхню S на гіперсфері радіусом R (Фіг. 1). Т-кут відрізняється від кластера тим, що охоплює нескінченну можливу кількість векторів n-вимірного гіпероб'єму Т-кута та охоплює не лише точки координат k,е векторів Х одного або кількох кластерів, але й нескінченну кількість точок всього простору k,е гіперкулі між точками з векторами Х . Разом з тим для Т-кута, який охоплює один кластер, при аналізі можна використовувати всі характеристики цього кластера: позначення кластера, його k,е k,е центроїд, кількість векторів кластера Х , параметри конкретних векторів Х . Як і при ієрархічній кластеризації великі Т-кути також можуть бути розділені на ієрархічно нижчі дрібніші Т-кути, коли адреса найменшого Т-кута характеризується переліком всієї зв'язаної сукупності Т-кутів, від великого Т-кута вищого ієрархічного рівня з великою кількістю k,е належних йому векторів Х , що входять у нього, до найдрібнішого Т-кута нижчого ієрархічного k,е рівня з меншою кількістю векторів Х , що належать йому і одночасно належать Т-куту вищого ієрархічного рівня. Розділ великих Т-кутів на ієрархічно нижчі та дрібніші Т-кути виконується за методом перенесення точки початку координат, приклад застосування якого наведений нижче. Розглянемо порядкову нумерацію Т-кутів, яка використовується як адреса Т-кута. В nвимірному просторі прямокутної системи координат позначення осей координат (х 1, х2,…, xj, …, хn) по знаках «+» чи «-» їх числових значень замінюють на коди "1" чи "0". Сукупність отриманих C C C C кодованих значень осей координат (х1 , х2 , …, xj , …, хn ) утворює порядковий номер відповідного Т-кута у двійковій системі числення. Цей двійковий порядковий номер Т-кута можна перевести у порядковий номер десяткової системи числення. Т-кут виділяється в гіперкулі сукупністю площин, кожна з яких охоплює початок координат та дві сусідні осі координат. На Фіг. 2 як приклад показані порядкові номери Т-кутів у десятковій системі числення g=0, g=1, g=2, g=3 для осей координат (x1, x2). Порядкові номери Т-кутів отримуються спочатку у двійковій системі числення, а потім переводяться у десяткову систему числення: - перший квадрант: (+х1, +х2) (1,1)  g=3; - другий квадрант: (-х1, +х2)  (0, 1)  g=1; - третій квадрант: (-х1, -х2)  (0, 0)  g=0; - четвертий квадрант: (+х1, -х2) (1,0)  g=2. Аналогічним чином можна отримати порядкові номери Т-кутів для системи координат із довільною кількістю осей координат. Отримані порядкові номери g не співпадають зі звичною загальноприйнятою нумерацією квадрантів на площині, а також не співпадають з відомою нумерацією октантів у тривимірній системі координат. Для стохастичного вектора невідомого класу X = (х1, х2,…, xj, …, хn) з числовими змінними C C C C можна отримати відповідну сукупність (х1 , х2 , …, xj , …, хn ), елементи якої складаються з 0 та 1 та яка є порядковим номером Т-кута вектора X у двійковій системі числення. C C Для можливості виділення окремих Т-кутів по їх порядкових двійкових номерах (х 1 , х2 , …, C C xj , …, хn ), використовують нейрони "T_AND_0" [4], які виконують складну логічну функцію (Фіг. 3). Нейрон "T_AND_0" має значення базисних змінних 0 та 1 і йому призначають для розпізнавання один з порядкових двійкових номерів Т-кутів з n розрядами, отриманий зі стохастичної навчальної вибірки для навчальних векторів. На відміну від звичайної логічної функції AND з двома вхідними змінними (х1, х2) зі значеннями 0 або 1, нейрон "T_AND_0" виконує аналогічну логічну операцію з n вхідними значеннями змінних (х 1, х2,…, xj, …, хn), α причому для отримання на виході сигналу 1 частка з вхідних змінних (на Фіг. 3 - змінні х j, α β α j=1,2,…, n ) повинна мати значення 1, а інша частка з вхідних змінних (на Фіг. 3 - змінні хj , j=n + α 1, n + 2,…, n) повинна мати значення 0. Пропонований спосіб навчання належить до стохастичних нейромереж прямого розповсюдження вхідного сигналу, які можуть мати мінімум два шари нейронів, а максимум три шари нейронів: 1-й вхідний шар кодування Т-кута, призначений для отримання порядкового номера Т-кута, у якому знаходиться вхідний вектор невідомого класу X = (х1, х2,…, xj, …, хn) з цифровими змінними xj. Порядкові номери всіх Т-кутів визначає експерт по даних початкової навчальної k,е вибірки стохастичних векторів Х для усіх ієрархічних рівнів λ у вигляді кодованих сукупностей C,λ C,λ C,λ C,λ C,λ X =(х1 , х2 ,…, xj ,…, хn ) з елементами 0 та 1; - 2-й шар складається з нейронів "T_AND_0", кожний з яких має призначений йому експертом для розпізнавання індивідуальний двійковий номер Т-кута типа k=0 або k=1, k,е C,λ отриманий експертом з навчальної вибірки стохастичних векторів Х . Якщо вектор входу X нейрона "T_AND_0" співпадає з призначеним йому експертом індивідуальним двійковим номером Т-кута, який нейрон "T_AND_0" повинен розпізнавати, то на виході цього нейрону "T_AND_0" 2-го шару сигнал 0 замінюється на сигнал 1; 5 UA 109297 U 5 10 15 20 25 - 3-й вихідний шар складається з нейронів-суматорів, на входи кожного з яких підключають виходи нейронів "T_AND_0" 2-го шару, призначених для розпізнавання Т-кутів типів k=0 однакового класу. 3-й вихідний шар відсутній у нейронній мережі у випадку, коли у 2-му шарі відсутні два чи більше нейронів "T_AND_0", призначених для розпізнавання Т-кутів типів k=0 однакового класу. Пропонований спосіб навчання стохастичної нейронної мережі розглянемо на основі вибірки з навчальних стохастичних векторів, яка зображена на Фіг. 4 у вигляді точок e=1,2,…, 15. Етап навчання нейронної мережі супроводжується паралельним будуванням її структурної схеми: на етапі навчання по даних Фіг. 4 послідовно визначають кількість ієрархічних рівнів у 1му та 2-му шарах, загальну кількість Т-кутів та їх типи k=0 і k=1 (тобто кількість нейронів у 2-му шарі і необхідність 3-го шару) і паралельно будуються відповідні елементі структурної схеми. У процесі навчання визначення елементів та параметрів нейронної мережі на наступних кроках залежать від отриманих даних навчання на попередніх кроках. Вагові коефіцієнти всіх входів нейронів прирівнюють 1 і не змінюють. Таким чином, структурна схема нейронної мережі є k,е різною для різних початкових навчальних вибірок стохастичних векторів Х . k,е k,е k,e Початкова навчальна вибірка стохастичних векторів Х = (х1 , х2 ), яка нижче використовується для будування нейронної мережі, наведена на Фіг. 4. Вона має розділювальні k,e обмеження у вигляді заборони мати вектори X різних класів у навчальній вибірці чи в групі k,е векторів. Всього початкова навчальна вибірка стохастичних векторів Х має 15 векторів (e=1,2,…, 15) трьох класів (і = 1, 2, 3). Кінцеві точки векторів для різних класів мають різну форму і позначені цифрами е= 1,2,…, 15. n У загальному випадку максимальна кількість Т-кутів дорівнює 2 . Наприклад, у п'ятимірному n 5 n 2 просторі маємо 2 =2 =32 Т-кута. Для Фіг. 4 максимальна кількість Т-кутів дорівнює 2 =2 =4. Згідно з початковою системою осей координат А з початком координат (х 1=0; х2=0) для k,е першого ієрархічного рівня λ = 1, всі навчальні вектори Х експерт вводить у табл. 1, в якій k,е вказує номер е кожного вектора Х , його клас, координати, двійковий d та десятковий g порядкові номери їх Т-кутів. Початок координат першого ієрархічного рівня λ = 1 приймається λ λ=1 k,e k,e k,e k,e k,e (х1 = 0; х2 =0), бо навчальні вектори вибірки X = (x1 , x2 ,…, xj ,…, xn ) вміщують змінні k,e xj з різними знаками при однакових нижніх індексах jλ. 30 Таблиця 1 λ=1 λ=1 Перший ієрархічний рівень λ = 1 з точкою початку координат (х1 =0; х2 =0). Порядкові номери k,с Т-кутів стохастичних векторів Х початкової навчальної вибірки k,e Дані навчального вектора Х Координати Номер Вектор Клас і k,e k,e,=1 k,e,=1 e X x1 ; x2 0,1 1 X 1 2; 20 0,2 2 X 1 3;20 0,3 3 X 1 2; 15 0,4 4 X 1 3; 15 0,5 5 X 1 3; 10 1,6 6 X 2 -1; 15 1,7 7 X 2 -3; 2,5 1,8 8 X 2 -0,8; 2,5 1.9 9 X 3 -1,2; 5,6 1,10 10 X 3 -3; 15 0,11 11 X 3 -3;-5 0,12 12 X 3 -2;-5 0,13 13 X 3 -1;-5 0,14 14 X 3 -3;-10 0,15 15 X 3 -2;-10 Порядкові номери Т-кутів Двійковий номер ТДесковий номер Т-кута g C C кута d = (x1 ; x2 ) 1;1 3 1;1 3 1;1 3 1;1 3 1;1 3 0;і 1 0;1 1 0;1 1 0; 1 1 0;1 1 0;0 0 0;0 0 0;0 0 0;0 0 0;0 0 k,с 35 У табл. 1 у верхньому індексі кожного вектора Х , керуючись данимиколонки класу, вказують значення типу k=0 або k=1 відповідного Т-кута. У табл. 1 сірий фон комірок призначений для чіткого розділу Т-кутів. Нижче для скорочення будемо посилатись лише на десяткові номери Т-кута g. З даних табл. 1 та Фіг. 4 на основі системи координат, поміченої літерою А, для першого ієрархічного рівня λ= 1 випливає: 6 UA 109297 U k, е 5 10 15 20 25 30 35 40 45 50 55 - у Т-куті g=0 присутні навчальні вектори Х одного класу і = 3. Тому Т-кут g=0 належить до типу k=0 (цей кут не має розділювальних обмежень стосовно належних йому векторів класу і = 3). Внаслідок цього вважаємо, що якщо у 1-му шарі нейронної мережі для першого ієрархічного рівня λ = 1 будь-який вхідний вектор X буде віднесений до Т-кута g=0, то цей вектор X має клас і = 3, а відповідний цьому Т-куту g=0 нейрон AND_A0 типу "T_AND_0" у 2-му шарі нейронної мережі (Фіг. 5) має призначений йому для запам'ятовування індивідуальний номер Т-кута g=0 (у двійковому численні). Кінцева частка позначення нейрона ANDA0 у вигляді "АО" означає: літера "А" - позначення осей координат на Фіг. 4; цифра "0" - порядковий номер Т-кута g=0 у вказаній системі координат А на Фіг. 4. Нейрон ANDA0 повинен мати вихідний сигнал розпізнавання класу і = 3. Але у даному випадку Т-кут g=0 охоплює лише частку навчальних векторів класу і = 3. Тому вихід нейрона AND_A0 з'єднують із входом нейрона-суматора i3 у 4-му вихідному шарі нейронів (Фіг. 5); у Т-куті g=1 присутні вектори двох класів (і = 2 та і = 3), і тому Т-кут належить до типу k=1 (цей кут має розділювальні обмеження, бо належні йому вектори належать до різних класів). Тому відповідний нейрон AND_A1 типу "T_AND_0" (Фіг. 5), який експерт призначає для запам'ятовування індивідуального номера g=1 Т-кута (у двійковому численні) не може мати вихідного сигналу. Належні Т-куту g=1 типу k=1 навчальні вектори мають різні класи, і тому ця скорочена сукупність навчальних векторів розглядаються як окрема скорочена стохастична k,e,=1 навчальна вибірка векторів X другого ієрархічного рівня λ = 2 з номерами навчальних векторів є = 6, 7, 8 (клас "і = 2") та e=9, 10 (клас "і = 3"). Відповідний нейрон AND_A1 Т-кута g=1 типу k=1 у 2-му шарі нейронної мережі розпізнає наданий йому індивідуальний номер g=1 і видає на виході сигнал 1 про виділення з розглянутої початкової навчальної вибірки з векторами e=1, 2,…, 15 нової скороченої вибірки нижчої ієрархії λ = 2 у вигляді сукупності відповідних навчальних векторів e=6, 7, 8, 9, 10, які попали у даний Т-кут типу k=1 і які потребують подальшого дроблення з використанням способу навчання нейронної мережі, аналогічного описаному вище; k,е - у Т-куті g=2 навчальні вектори Х відсутні, і далі Т-кут g=2 не аналізують; k,е - у Т-куті g=3 присутні навчальні вектори Х одного класу і = 1. Тому Т-кут g=3 відносять до типу k=0 (цей кут не має розділювальних обмежень стосовно належних йому векторів класу і = 1). Внаслідок цього вважають, що якщо у 1-му шарі нейронної мережі для першого ієрархічного рівня λ = 1 будь-який вхідний стохастичний вектор невідомого класу X = (х1, х2,…, xj, …, хn) відносять до Т-кута g=3, то цей вектор X має клас і = 1. Тому відповідному нейрону AND_A3 типу "T_AND_0" у 2-му шарі нейронної мережі (Фіг. 5) призначають для запам'ятовування індивідуальний номер Т-кута g=3 (у двійковому численні). Кінцева частка позначення нейрона ANDA3 у вигляді "A3" означає: літера "А" - позначення осей координат на Фіг. 4; цифра "3" порядковий номер Т-кута g=3 у вказаній системі координат А на Фіг. 4. Нейрону AND_A3 надають вихідний сигнал розпізнавання класу і = 1, тому що згідно з табл. 1 відповідний йому Ткут g=3 (Фіг. 5) охоплює всі навчальні вектори класу і = 1 за порядковими номерами є = 1, 2, 3, 4, 5 початкової навчальної вибірки. Таким чином, на першому ієрархічному рівні λ=1 згідно з даними табл. 1 та Фіг. 4 з системою k,e координат, поміченою літерою А, експерт розділяє навчальні стохастичні вектори X початкової навчальної вибірки серед Т-кутів типу k=0 та k=1; в результаті отриманий лише один Т-кут g=1 типу k=1 з навчальними векторами є = 6, 7, 8, 9, 10, сукупність яких експерт розглядає як ієрархічно нижчу скорочену навчальну вибірку, яку потрібно далі розділяти на наступні менші частки з метою отримання ієрархічно нижчих Т-кутів типу k=0. Для нижчого ієрархічного рівня λ = 2 точку центра нової системи координат (х1=2, х2=2) для Т-кута g=1 типу k=1 вищого ієрархічного рівня λ =1 експерт може визначати по-різному: може довільно задати координати всередині Т-кута g=1 типу k=1; може розрахувати координати як кінцеву точку центроїда векторів e=6, 7, 8, 9, 10, які належать цьому куту; може визначити координати, як деяку "точку центра тяжіння" площі ("гіпероб'єму") Т-кута з осями координат (-x1; +х2). У даному випадку вважаємо, що на Фіг. 4 експерт визначив осями, позначеними літерою В, центр нової системи координат (х1=2 = -1,5; х2=2 = +10) для Т-кута g=1 типу k=1 ієрархічного рівня λ = 1. Для всіх навчальних векторів e=6, 7, 8, 9, 10, які знаходяться в Т-куті g=1 типу k=1 k,e,=2,H ієрархічного рівня λ = 1, експерт перераховує значення їх нових координат за формулою xj k,e,=1 λ=2 = (xj -xj ) і вводить їх у табл. 2 з виконанням у ній розрахунків, аналогічних табл. 1. 7 UA 109297 U Таблиця 2 λ=2 λ=2 Другий ієрархічний рівень λ = 2 з точкою початку координат (х1 = -1,5; x2 = +10). k,е Порядкові номери Т-кутів стохастичних векторів Х , e=6, 7, 8, 9, 10 скороченої навчальної вибірки нижчої ієрархії λ = 2 k,e Дані навчального вектора X Координати Номер Вектор Клас і k,е k,e,=2 k,e,=2 e X x1 ; x2 0,1 6 X 2 +0,5; +5 0,7 7 X 2 -1,5;-7,5 1,8 8 X 2 +0,7; -7,5 1,9 9 X 3 +0,3; -4,4 0,10 10 X 3 -1,5;+5 Порядкові номери Т-кутів Двійковий номер Т- Десятковий номер Т-кута C C кута d = (x1 ; x2 ) g 1;1 3 0;0 0 1;0 2 1;0 2 0;1 1 k,е 5 10 15 20 25 30 35 40 У табл. 2 у верхньому індексі кожного вектора Х вказують значення типу k відповідного Ткута. З даних табл. 2 та Фіг. 4 для другого ієрархічного рівня λ = 2 за системою координат, поміченою літерою В, випливає: k,е=7 - у Т-куті g=0 присутній навчальний вектор Х одного класу і = 2. Тому Т-кут g=0 належить до типу k=0. Відповідний цьому Т-куту g=0 нейрон AND_B0 типу "T_AND_0" у 2-му шарі нейронної мережі (Фіг. 5) має призначений йому для запам'ятовування індивідуальний номер Ткута g=0 (у двійковому численні). Але у даному випадку Т-кут g=0 охоплює лише частку навчальних векторів класу і = 2. Тому вихід нейрона AND_B0 з'єднують із входом нейронасуматора i2 у 3-му вихідному шарі (Фіг. 5); k,е=10 - у Т-куті g=1 присутній навчальний вектор X одного класу і = 3. Тому Т-кут g=1 належить до типу k=0. Відповідний цьому Т-куту g=1 нейрон AND_B 1 типу "T_AND_0" у 2-му шарі нейронної мережі (Фіг. 5) має призначений йому для запам'ятовування індивідуальний номер Ткута g-1 (у двійковому численні). Але у даному випадку Т-кут g=1 охоплює лише частку навчальних векторів класу і = 3. Тому вихід нейрона AND_B1 з'єднують з входом нейронасуматора i3 у 3-му вихідному шарі (Фіг. 5); - у Т-куті g=2 присутні два вектори двох класів (один класу і = 2 та інший класу і = 3), і тому Т-кут належить до типу k=1. Тому експерт призначає нейрону AND_B2 типу "T_AND_0" (Фіг. 5) для запам'ятовування індивідуальний номер Т-кута g=2 (у двійковому численні). Належні Т-куту g=2 типу k=1 навчальні вектори мають різні класи, внаслідок чого ця скорочена сукупність k,е навчальних векторів Х , e=8, 9, розглядається як окрема скорочена стохастична навчальна вибірка векторів X третього ієрархічного рівня λ = 3 з номерами e=8 (клас і = 2) та e=9 (клас і = 3). Відповідний нейрон ANDJB2 Т-кута g=2 типу k=1 у 2-му шарі нейронної мережі розпізнає наданий йому індивідуальний номер g=2 і видає на виході сигнал 1 про виділення з розглянутої початкової навчальної вибірки з векторами e=6, 7, 8, 9, 10 нової скороченої вибірки для нижчої ієрархії λ = 3 у вигляді сукупності відповідних навчальних векторів є = 8, 9, які попали у даний Ткут типу k=1 і які потребують подальшого дроблення з використанням способу навчання нейронної мережі, аналогічного описаному вище; k,e=6 - у Т-куті g=3 присутній навчальний вектор Х одного класу і = 2. Тому Т-кут g=3 належить до типу k=0. Відповідний цьому Т-куту g=3 нейрон AND_B3 типу "T_AND_0" у 2-му шарі нейронної мережі (Фіг. 5) має призначений йому для запам'ятовування індивідуальний номер Ткута g=3 (у двійковому численні). Тому що Т-кут g=3 охоплює лише частку навчальних векторів класу і - 2, вихід нейрона AND_B3 з'єднують із входом нейрона-суматора i3 у 3-му вихідному шарі (Фіг. 5). Для навчальних векторів є = 8, 9 (табл. 2), які знаходяться в Т-куті g=2 типу k=1 ієрархічного λ=3 λ=3 рівня λ = 2, експерт визначає точку початку координат (х1 = - 0,9; х2 = +3), перераховує k,e,=3,H k,e,=1 λ=3 значення їх нових координат за формулою xj = (xj -xj ) і вводить їх у табл. 3 з виконанням у ній розрахунків, аналогічних табл. 1 та табл. 2. 8 UA 109297 U Таблиця 3 λ=3 λ=3 Третій ієрархічний рівень λ = 3 з точкою початку координат (х3 = - 0,9; x2 = +3). k,е Порядкові номери Т-кутів стохастичних векторів Х , e=8, 9, скороченої навчальної вибірки нижчої ієрархії λ = 3 k,e Дані навчального вектора X Координати Номер Вектор Клас і k,e k,e,=3 k,e,λ=3 e X (xj -xj ) 0,8 8 X 2 +0,1;-0,5 0,9 9 X 3 -0,3; +2,6 Порядкові номери Т-кутів Двійковий номер Т- Десятковий номер Т-кута C C кута d = (x1 ; x2 ) g 1;0 2 0;1 1 k,е 5 10 15 20 25 30 35 40 45 У табл. 3 у верхньому індексі кожного вектора X вказують значення типу k відповідного Ткута. Для третього ієрархічного рівня λ = 3 з табл. 3 та Фіг. 4 з системою координат, поміченою літерою С, випливає: k,е - у Т-кутах g=0 та g=3 ієрархічного рівня λ= 3 відсутні навчальні вектори Х , і тому Т-кути g=0 та g=3 не аналізуються; k,е=9 - у Т-куті g=1 ієрархічного рівня λ = 3 присутній один навчальний вектор X , класу і = 3. Тому Т-кут g=1 належить до типу k=0. Відповідний цьому Т-куту g=1 нейрон AND_C1 типу "T_AND_0" у 2-му шарі нейтронної мережі (Фіг. 5) має призначений йому для запам'ятовування індивідуальний номер Т-кута g=1 (у двійковому численні). Але у даному випадку Т-кут g=1 охоплює лише частку навчальних векторів класу і = 3. Тому вихід нейрона AND СІ з'єднують із входом нейрона-суматора i3 у 3-му вихідному шарі (Фіг. 5); k,e=9 - у Т-куті g=2 ієрархічного рівня λ = 3 присутній один навчальний вектор Х класу і = 2. Тому Т-кут g=2 належить до типу k=0. Відповідний цьому Т-куту g=2 нейрон AND_C2 типу "T_AND_0" у 2-му шарі нейронної мережі (Фіг. 5) має призначений йому для запам'ятовування індивідуальний номер Т-кута g=2 (у двійковому численні). Але у даному випадку Т-кут g=2 охоплює лише частку навчальних векторів класу і = 2. Тому вихід нейрона AND_C2 з'єднують з входом нейрона-суматора і = 2 у 3-му вихідному шарі (Фіг. 5). На Фіг. 5 кожний ієрархічно нижчий рівень при λ > 1 має індивідуальний визначений для λ даної скороченої вибірки центр координат X , а кожний з нейронів T_AND_0 2-го шару нижчих рівнів має додатковий (п + 1)-й вхід, який з'єднують із виходом відповідного нейрона T_AND_0 у 2-му шарі попереднього вищого ієрархічного рівня, що контролює групу відповідних навчальних k,e,λ векторів Х типу k=1 нижчого рівня. У результаті нейрон найнижчого ієрархічного рівня λ = 3 типу T_AND_0 у 2-му шарі має вихідний сигнал для Т-кута типу k=0 лише у випадку наявності сигналів виходів у всіх відповідних нейронів типу T_AND_0 вищих ієрархічних рівнів. k,e,=1 Будування навченої нейронної мережі продовжується до охоплення всіх векторів X вищого ієрархічного рівня λ = 1 всіма вихідними сигналами Т-кутів типу k=0 з 2-го та 3-го шарів, по яких визначають клас вхідного вектора X. Розглянемо процес використання отриманої нейронної мережі Фіг. 5 на прикладі появи на її входах у 1-му шарі координат вектора X (х1=2; x2=5) Фіг. 4. Порядковий номер Т-кута вектора X в двійковій системі числення дорівнює d=11, а в десятковій системі числення g=3. Цей сигнал C,=1 C,=1 C,=2 C,=2 C,=3 C,=3 попадає на входи всіх ієрархічних рівнів нейронів (x1 , x2 ), (x1 , x2 ), (x1 , x2 ) на виходах яких з'являються вихідні сигнали, перераховані згідно з заданими центрами координат для кожного ієрархічного рівня λ. Але у нейрона AND_A1 вихідний сигнал дорівнює нулю, і тому вихідні сигнали нейронів нижчого рівня AND_B0, AND_B1, AND_B2, AND_B3, AND_C1, AND_C2 теж дорівнюють нулю. У даному випадку вихідний сигнал, рівний 1, має лише один нейрон AND_A3, який і видасть вихідний сигнал нейронної мережі про належність вхідного невідомого вектора X до класу і = 3. Розглянемо застосування пропонованого способу навчання стосовно нейронної мережі з використанням кластерів. Згідно з описаним вище способом навчання, з кожним вихідним нейроном 2-го шару Фіг. 5, які охоплюють Т-кути типу k=0, пов'язана визначена сукупність навчальних векторів, тобто пов'язаний відповідний кластер. У табл. 4 наведений взаємний зв'язок отриманих вище на першому етапі навчання груп навчальних векторів (кластерів) з позначеннями відповідних нейронів-центроїдів кластерів. 9 UA 109297 U Таблиця 4 Взаємний зв'язок отриманих на першому етапі навчання груп навчальних векторів (кластерів) з позначеннями відповідних нейронів-центроїдів Дані першого етапу навчання Позначення Дані кластера нейрона на Фіг. 5 AND_A0 Вектори e=11-15; клас і = 3 (табл. 1) AND_A3 Вектори e=1 - 5; клас і = 1 (табл. 1) AND_B0 Вектор e=7; клас і = 2 (табл. 2) AND_B1 Вектор e=10; клас і = 3 (табл. 2) AND_B3 Вектор e=6; клас і - 2 (табл. 2) AND_C1 Вектор e=8; клас і = 3 (табл. 3) AND_C2 Вектор e=9; клас і = 2 (табл. 3) 5 10 15 20 25 30 35 40 45 Другий етап навчання Позначення нейронів-центроїдів кластерів А0 A3 В0 B1 B3 С1 С2 Кожний подібний кластер можна замінити центроїдам кластера і використати центроїди для класифікації векторів X невідомого класу. Тому на етапі навчання і будування нейронної мережі визначають всі Т-кути типу k=0, які k,e,=1 охоплюють всі навчальні вектори X вищого ієрархічного рівня λ = 1, і дають їм порядкові номери δ = 1, 2,…, q. Всі Т-кути типу k=0 по належних їм групах навчальних векторів замінюють відповідними центроїдами кластерів та будують нейронну мережу при відомій кількості кластерів q і при відомих координатах їх центроїдів. У результаті 1-й шар нейронної мережі складають з n нейронів з одним входом та одними виходом, у якому нормалізують і розмножують змінні вхідного стохастичного вектора невідомого класу X = (х1, х2,…, xj, …, хn), у 2-й шар вводять q нейронів з порядковими номерами δ = 1, 2,…, q, кожному з яких надають n входів з ваговими коефіцієнтами, рівними координатам відповідних центроїдів кластерів, а n входів кожного з qнейронів 2-го шару з'єднують з відповідними виходами 1-го шару нейронів. δ На виході кожного з q нейронів 2-го шару визначають значення сигнала виходу М , як підсумок добутків змінних вхідного вектора X та відповідних вагових коефіцієнтів входів, у 3-му шарі з q входами та q виходами за принципом "переможець отримує все" по найбільшому значенню виходу серед q нейронів 2-го шару призначають вихідний сигнал 1 для кластерапереможця при нульових сигналах виходу для всіх інших кластерів. Виходи кожної сукупності нейронів 3-го шару, якщо вона належить до однакового класу, задовольняє умовам типу k=0, і якщо сукупність вміщує в 3-му шарі два і більше нейронів, з'єднують із відповідними входами з ваговими коефіцієнтами 1 нейрона-суматора у 4-му вихідному шарі. Для класифікації невідомого стохастичного вхідного вектора X = (х1, х2,…, хn) використовують виходи нейронів-суматорів 4-го вихідного шару та виходи нейронів 3-го шару, якщо вони не з'єднані з входами нейронів 4-го вихідного шару. На етапі використання нейронної мережі, отриманої на основі центроїдів кластерів, на входи 1-го шару подають вхідний стохастичний вектор невідомого класу X = (х1, х2,…, xj, …, хn), стосовно якого у 2-му шарі отримують оцінки близькості вектора X до кожного з q центроїдів груп векторів Т-кутів типу k=0, у 3-му шарі по найбільшій величині виходу визначають переможця, а по вихідних сигналах 3-го та 4-го шарів класифікують вхідний вектор X. Розглянемо застосування пропонованого способу навчання стосовно нейронної мережі з використанням кластерів у випадку оцінки міри близькості до кластера за допомогою байєсового класифікатора. У цьому випадку на етапі навчання при будуванні нейронної мережі у кожному з q нейронів δ 2-го шару визначають значення М як підсумок добутків змінних вхідного вектора X та відповідних вагових коефіцієнтів входів, а в активаційній функції кожного з q нейронів 2-го шару визначають значення сигнала виходу у вигляді байєсового класифікатора i i δ δ APf M , i де А - витрати внаслідок помилкового заперечення наявності відповідного і-го класу даного кластера при його реальній присутності; i Р - апріорна ймовірність появи і-го класу даного кластера, яку або визначають по опублікованих даних, або приймають рівною відношенню кількості векторів і-го класу в початковій навчальній вибірці до загальної кількості навчальних векторів Е в початковій вибірці; 10 UA 109297 U δ 5 10 15 20 f - оцінка частотної характеристики даного δ-го кластера Т-кута типу k=0, яку приймають рівною відношенню кількості векторів і-го класу в δ-му кластері до загальної кількості векторів іго класу в початковій вибірці. У всьому іншому робота нейронної мережі з використанням кластерів не змінюється. Пропонований спосіб навчання стохастичної нейронної мережі зменшує витрати на стохастичну нейронну мережу та на її обслуговування через зменшення кількості нейронів і заміни векторами центроїдів кластерів інформації початкової навчальної вибірки стохастичних векторів. Використана інформація: 1. Specht D.F. Probabilistic Neural Network for Classification, Mapping and Associative Memory // Proc. of the IEEE Int. Conf. on Neural Network, San Diego, 1988. - Vol. 1. - P. 525-532. 2. Руденко О.Г., Бодянський С.В. Штучні нейронні мережі. - Харків: ТОВ "Компанія СМІТ", 2006. - 404 с. 3. Каллан Роберт. Основные концепции нейронных сетей: Пер. с англ. -М.: Издательский дом "Вильяме", 2003. - 288 с. 4. Кутковецький В.Я., Турти М.В. Нейрон "T_AND_0". Патент України на корисну модель, G06N 3/00, № 97526, 10.04.2015, Бюл. №7.-3 с. 5. Tryon R.C. Cluster analysis. - London: Ann Arbor Edwards Bros, 1939. -139 p. 6. Дюран Б., Оделл П. Кластерный анализ. - М.: Статистика, 1977. - 128 с. 7. Классификация и кластер. Под ред. Дж. Вэн Райзина. - М.: Мир, 1980. - 390 с. 8. Мандель И. Д. Кластерный анализ. - М.: Финансы и статистика, 1988. - 176 с. ФОРМУЛА КОРИСНОЇ МОДЕЛІ 25 30 35 40 45 50 55 60 1. Спосіб навчання стохастичної нейронної мережі, за яким класифікують вхідний стохастичний вектор невідомого класу X=(х1, х2, ..., хj, ..., хn), де j=1, 2, ..., n - порядковий номер числової k,е k,е змінної xj вектора X, на основі початкової навчальної вибірки стохастичних векторів Х =(х1 , k,е k,е k,е k,е х2 , ..., xj , ..., хn ), де k=0 - тип навчальної вибірки векторів X чи окремих навчальних груп k,е вибірки з векторами X , серед яких відсутні вектори різних класів чи вектори з іншими розділювальними обмеженнями, під якими також розуміють заборону мати у навчальній вибірці k,е k,е чи у її групі вектори X із забороненими відстанями між векторами X або із забороненими k,е стохастичними показниками вибірки чи її групи та ін., k=1 - тип навчальної вибірки векторів X k,е чи окремих навчальних груп вибірки з векторами X , серед векторів яких присутні k,е розділювальні обмеження, j=1, 2, ..., n - порядковий номер числової змінної xj навчального k,е k,е вектора X , e=1, 2, ..., Е - порядковий номер навчального вектора X у навчальній вибірці, який відрізняється тим, що на етапі навчання будують нейронну мережу на основі використання k,е навчальної вибірки з векторами X , для чого вагові коефіцієнти входів всіх нейронів нейронної мережі прирівнюють 1 і не змінюють, нейронній мережі надають обов'язкові 1-й і 2-й шари нейронів та необов'язковий 3-й шар нейронів, з яких 1-й та 2-й шари нейронів можуть мати ряд паралельних ієрархічних аналогічних шарів нейронів, кожному з яких призначають індивідуальну вибірку навчальних векторів та визначають на основі даних цієї індивідуальної вибірки відповідний центр координат X - (х1, х2 ..., хj ..., хn), де  - 1, 2, 3, ... - порядковий номер ієрархії, у 1-му шарі на етапі навчання для вищого першого ієрархічного рівня =1 призначають як індивідуальну вибірку початкову навчальну вибірку, для цієї вибірки визначають центр координат X=1 - (х1=1, х2=1 ..., хj=1 ..., хn=1), у якому значення координат xj=1 прирівнюють k,е нулю (xj=1=0), якщо навчальні вектори X вибірки вміщують змінні xj=1 з різними знаками при однакових нижніх індексах j, а у іншому разі елементи центра координат X=1 прирівнюють координатам серединної точки початкової вибірки у вигляді, наприклад, координат кінцевої точки вектора центроїда відповідних векторів або точки "центру тяжіння" відповідного Т-кута k,е типу k=1, перераховують координати навчальних векторів X початкової навчальної вибірки на k,e,=1 k,e,=1 координати навчальних векторів для нового центра координат X у вигляді X - (х1 , k,e,=1 k,e,=1 k,e,=1 k,e.=1 k,е, =1 х2 ..., хj ..., хn )], де xj = (xj -xj ), у 1-й шар вводять n нейронів першого ієрархічного рівня  = 1, кожний з яких має один вхід, що з'єднують на етапі навчання з k,e,=1 k,e,=1 числовою змінною хj вхідного навчального вектора Х індивідуальної навчальної C,=1 вибірки, і має один вихід, на якому отримують для j-гo нейрона або код xj =0, якщо знак k,е,=1 C, =1 C,=1 різниці (xj , xj =1) є від'ємним, або у іншому разі - код xj =1, а сукупність виходів X C,=1 C,=1 C,=1 C,=1 (х1 , х2 ..., хj ..., хn ) всіх n нейронів 1-го шару у першому ієрархічному рівні =1 розглядають як розряди двійкового числа і вважають сукупність значень цих розрядів порядковим номером у двійковій системі числення відповідного Т-кута типу k=0 або k=1, у 2-й шар першого ієрархічного рівня =1 вводять нейрони типу T_AND_0, кількість яких дорівнює 11 UA 109297 U 5 10 15 20 25 30 35 40 45 50 55 загальній кількості Т-кутів типів k=0 та k=1 початкової навчальної вибірки з навчальними k,e,=1 векторами X першого ієрархічного рівня =1, для кожного нейрона типу T_AND_0 вводять n входів, які з'єднують з відповідними n виходами нейронів 1-го шару першого ієрархічного рівня =1, кожному нейрону типу T_AND_0 призначають для розпізнавання індивідуальний порядковий двійковий номер Т-кута, рівний одному з порядкових двійкових номерів Т-кутів k,e,=1 початкової вибірки з навчальними векторами X , якщо частка початкової навчальної вибірки k,e,=1 k,e,=1 векторів X , розміщена в Т-куті типу k=0, який охоплює всі навчальні вектори X даного класу, то на виході відповідного нейрона T_AND_0 для Т-кута типу k=0 отримують вихідний сигнал відповідного класу стохастичної нейронної мережі, якщо частка початкової навчальної k,e,=1 вибірки векторів X розміщена в Т-куті типу k=0, який охоплює лише частку навчальних k,e,=1 векторів X даного класу, то вихід відповідного нейрона T_AND_0 для Т-кута типу k=0 з'єднують із входом відповідного нейрона-суматора 3-го шару нейронів, на виході якого отримують вихідний сигнал для одного з відповідних класів нейронної мережі, і вводять для цього нейрона-суматора 3-го шару нейронів кількість входів, яка дорівнює кількості Т-кутів типу k,e,=1 k=0, у які попали навчальні вектори X даного одного класу, якщо частка початкової навчальної вибірки векторів X розміщена в Т-куті типу k=1, то всі належні даному Т-куту типу k,e,=1 k=1 навчальні вектори X різних класів розглядають як окрему скорочену стохастичну навчальну вибірку нижчої ієрархії, яка потребує подальшого розділу на частки з використанням способу навчання нейронної мережі, аналогічного описаному вище, сигнал виходу нейрона T_AND_0 для Т-кута типу k=1 розглядають як сигнал дозволу на вихід відповідного сигналу нижчої ієрархії, вихід цього нейрона Т AND 0 з'єднують з додатковим (n + 1)-м входом до ієрархічно нижчого нейрона T_AND_0 для Т-кутів типу k=0 та k=1 при ієрархічних рівнях >1, для чого в нейронну мережу у 1-му та 2-му шарах при ієрархічних рівнях >1 вводять нові ієрархічно нижчі рівні із загальною кількістю ієрархічно нижчих шарів, яка дорівнює кількості наявних у вищому ієрархічному рівні Т-кутів типу k=1, а кожний з ієрархічно нижчих рівнів має у 1-му та 2-му шарі структуру та зв'язки, аналогічні описаним вище для вищого ієрархічного рівня =1, за винятком того, що кожний ієрархічно нижчий рівень при >1 має індивідуальний визначений для даної скороченої вибірки центр координат X, а кожний з відповідних нейронів T_AND_0 2-го шару нижчих ієрархічних рівнів має додатковий (n + 1)-й вхід, який з'єднують із виходом відповідного нейрона T_AND_0 попереднього вищого ієрархічного рівня, що вміщує k,e, групу відповідних навчальних векторів X типу k=1 нижчого рівня, з наступним повторним дробленням ієрархічно нижчих скорочених вибірок навчальних векторів Т-кутів типу k=1 до k,e,=1 охоплення всіх векторів X вищого ієрархічного рівня =1 всіма вихідними сигналами Т-кутів типу k=0 з 2-го та 3-го шарів, по яких визначають клас вхідного вектора X, а на етапі використання нейронної мережі на всі ієрархічні входи всіх ієрархічних рівнів  1-го шару подають вхідний стохастичний вектор невідомого класу X, на виходах всіх ієрархічних шарів 1го шару отримують виходи результатів кодування різниць (х j - xj) у вигляді двійкових C, порядкових номерів X відповідних Т-кутів типу k=0 або k=1, у які може попасти вхідний вектор невідомого класу X, у 2-му шарі вмикають на подальше дроблення скорочені вибірки навчальних векторів Т-кутів типу k=1 на ієрархічно нижчих рівнях 1 -го та 2-го шарів, нейрони 2го шару типу T_AND_0 по отриманому Т-куту типу k=0 класифікують вхідний вектор X, а у 3-му шарі, який не є обов'язковим, об'єднують на нейронах-суматорах сигнали з 2-го шару від виходів нейронів типу T_AND_0, що розпізнають індивідуальні номери Т-кутів типу k=0 однакових класів. 2. Спосіб навчання нейронної мережі за п. 1, який відрізняється тим, що на етапі навчання при будуванні нейронної мережі визначають за п. 1 Т-кути типу k - 0, що охоплюють всі навчальні k,e,=1 вектори X вищого ієрархічного рівня = 1, дають їм порядкові номери  = 1, 2, ..., q, і всі Ткути типу k=0 по належних їм групах навчальних векторів замінюють відповідними центроїдами кластерів, будують нейронну мережу при відомій кількості кластерів q та при відомих координатах їх центроїдів, для чого 1-й шар нейронної мережі складають з n нейронів з одним входом та одними виходом, у якому нормалізують і розмножують змінні вхідного стохастичного вектора невідомого класу X=(х1, х2, ..., хj, ..., хn), у 2-й шар вводять q нейронів з порядковими номерами  = 1, 2,..., q, кожному з яких надають n входів з ваговими коефіцієнтами, рівними координатам відповідних центроїдів кластерів, n входів кожного з q нейронів 2-го шару з'єднують з відповідними виходами 1-го шару нейронів, на виході кожного з q нейронів 2-го шару визначають значення сигналу виходу М, як підсумок добутків змінних вхідного вектора X та відповідних вагових коефіцієнтів входів, у 3-му шарі з q входами та q виходами за принципом "переможець отримує все" по найбільшому значенню виходу серед q нейронів 2-го шару призначають вихідний сигнал 1 для кластера-переможця при нульових сигналах виходу для всіх 12 UA 109297 U 5 10 15 20 інших кластерів, виходи кожної сукупності нейронів 3-го шару, якщо вона належить до однакового класу, задовольняє умовам типу k=0 і якщо сукупність вміщує в 3-му шарі два і більше нейронів, з'єднують з відповідними входами з ваговими коефіцієнтами 1 нейронасуматора у 4-му вихідному шарі, для класифікації невідомого стохастичного вхідного вектора X=(х1, х2, ..., хn) призначають виходи нейронів-суматорів 4-го вихідного шару та виходи нейронів 3-го шару, якщо вони не з'єднані з входами нейронів 4-го вихідного шару, на етапі використання нейронної мережі на входи 1-го шару подають вхідний стохастичний вектор невідомого класу X=(х1, х2, ..., хj, ..., хn), стосовно якого у 2-му шарі отримують оцінки близькості вектора X до кожного з q центроїдів груп векторів Т-кутів типу k=0, у 3-му шарі по найбільшій величині виходу визначають переможця, а по вихідних сигналах 3-го та 4-го шарів класифікують вхідний вектор X. 3. Спосіб навчання нейронної мережі за п. 2, який відрізняється тим, що на етапі навчання при будуванні нейронної мережі у кожному з q нейронів 2-го шару визначають значення М, як підсумок добутків змінних вхідного вектора X та відповідних вагових коефіцієнтів входів, а в активаційній функції кожного з q нейронів 2-го шару визначають значення сигналу виходу у i i i вигляді байєсового класифікатора A P fM, де А витрати внаслідок помилкового заперечення i наявності відповідного і-го класу даного кластера при його реальній присутності; Р - апріорна ймовірність появи і-го класу даного кластера, яку або визначають по опублікованих даних, або приймають рівною відношенню кількості векторів і-го класу в початковій навчальній вибірці до загальної кількості навчальних векторів Е в початковій вибірці; f - оцінка частотної характеристики даного -го кластера Т-кута типу k=0, яку приймають рівною відношенню кількості векторів і-го класу в -му кластері до загальної кількості векторів і-го класу в початковій вибірці. 13 UA 109297 U 14 UA 109297 U Комп’ютерна верстка Л. Литвиненко Державна служба інтелектуальної власності України, вул. Василя Липківського, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут інтелектуальної власності”, вул. Глазунова, 1, м. Київ – 42, 01601 15