Обробка даних зображення, що містять результати турбулентності у рідкому середовищі
Формула / Реферат
1. Спосіб обробки послідовних цифрових даних зображення, отриманих за допомогою камери, зануреної в рідину, що містить явища турбулентності, які викликають ефект видимого зсуву пікселів зображень, що містить етапи, на яких:
моделюють ефект турбулентності на пікселях зображень, та
виконують обернення згортки за допомогою згаданого моделювання, усередненого за часом зображення.
2. Спосіб за п. 1, який відрізняється тим, що на етапі моделювання виконують оцінку моделі щільності вірогідності вектора ![]() зсуву, що належить до ефекту турбулентності.
зсуву, що належить до ефекту турбулентності.
3. Спосіб за п. 2, який відрізняється тим, що згадана модель належить до типу з експоненціальним зменшенням.
4. Спосіб за п. 3, який відрізняється тим, що згадана модель ![]() виражена як функція вектора
виражена як функція вектора ![]() рівнянням вигляду:
рівнянням вигляду:
![]() ,
,
де:
![]() - середньоквадратичне відхилення норми вектора
- середньоквадратичне відхилення норми вектора ![]() ,
,
![]() і
і ![]() - позитивні речові константи.
- позитивні речові константи.
5. Спосіб за п. 4, який відрізняється тим, що ![]() і
і ![]() .
.
6. Спосіб за будь-яким з пп. 1-5, який відрізняється тим, що усереднене за часом зображення оцінюють по середньому значенню, зваженому по ступенях фактора забування, що відповідно зменшується залежно від часу.
7. Спосіб за п. 6, який відрізняється тим, що середнє зображення ![]() , що оцінюється у час
, що оцінюється у час ![]() для пікселя з векторними координатами
для пікселя з векторними координатами ![]() , визначається наступним чином:
, визначається наступним чином:
![]() ,
,
де член ![]() є дійсним числом, відповідним фактору забування.
є дійсним числом, відповідним фактору забування.
8. Спосіб за будь-яким з пп. 1-7, який відрізняється тим, що усереднене за часом зображення оцінюють з використанням рекурсивної часової фільтрації.
9. Спосіб за п. 8, який відрізняється тим, що ![]() -ий вихід часового фільтра для моменту часу
-ий вихід часового фільтра для моменту часу ![]() , позначений як
, позначений як ![]() , і середнє зображення
, і середнє зображення ![]() зв'язані між собою рівняннями:
зв'язані між собою рівняннями:
![]() ,
,
![]() .
.
10. Спосіб за будь-яким з пп. 6, 7 та 9, який відрізняється тим, що фактор ![]() забування вибирають рівним 0,99.
забування вибирають рівним 0,99.
11. Спосіб за будь-яким з пп. 1-10, який відрізняється тим, що на етапі виконання обернення згортки застосовують лінійну просторову фільтрацію до виразу, відповідного згаданому моделюванню.
12. Спосіб за п. 11, який відрізняється тим, що фільтрація є фільтрацією типу Вінера.
13. Спосіб за п. 12, який відрізняється тим, що просторовий фільтр заданий в спектральній області наступними формулами:
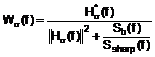 , якщо
, якщо ![]() ,
,
![]() , якщо
, якщо ![]() ,
,
де:
![]() - двовимірний вектор двох частот, що нормуються після двовимірного перетворення Фур'є,
- двовимірний вектор двох частот, що нормуються після двовимірного перетворення Фур'є,
![]() - частота відсічення фільтра для усунення будь-якої потенційної спектральної ступінчастості,
- частота відсічення фільтра для усунення будь-якої потенційної спектральної ступінчастості,
![]() і
і ![]() - відповідно щільності спектральної потужності шумів та різкого зображення, що підлягає визначенню, та
- відповідно щільності спектральної потужності шумів та різкого зображення, що підлягає визначенню, та
![]() - двовимірне перетворення Фур'є щільності вірогідності ефекту турбулентності
- двовимірне перетворення Фур'є щільності вірогідності ефекту турбулентності ![]() .
.
14. Спосіб за п. 13, який відрізняється тим, що просторовий фільтр виражений наступним рівнянням:
![]() ,
,
де член ![]() виражений як функція параметрів, вибраних таким чином, що член
виражений як функція параметрів, вибраних таким чином, що член ![]() знаходиться в діапазоні від 10-2 до 10-4.
знаходиться в діапазоні від 10-2 до 10-4.
15. Спосіб за будь-яким з пп. 13 або 14, який відрізняється тим, що двовимірне перетворення Фур'є ![]() щільності вірогідності ефекту турбулентності
щільності вірогідності ефекту турбулентності ![]() задане наступним рівнянням:
задане наступним рівнянням:
![]() ,
,
де ![]() - позитивна речова константа, а
- позитивна речова константа, а ![]() є позитивним дійсним числом, підрахованим за кількістю пікселів.
є позитивним дійсним числом, підрахованим за кількістю пікселів.
16. Спосіб за п. 15, який відрізняється тим, що двовимірне перетворення Фур'є ![]() визначається наступною формулою:
визначається наступною формулою:
![]() ,
,
де ![]() знаходиться в діапазоні від 0 до 30 пікселів.
знаходиться в діапазоні від 0 до 30 пікселів.
17. Спосіб за будь-яким з пп. 1-16, який відрізняється тим, що згадана камера поступально переміщається, при цьому застосовують зміну положення попереднього зображення до поточного зображення для оцінки середнього зображення.
18. Спосіб за п. 17, який відрізняється тим, що додатково містить етап, на якому виконують часову фільтрацію із зміною положення та нормуванням.
19. Спосіб за п. 18, який відрізняється тим, що додатково містить етапи, на яких:
виконують скидання за допомогою:
![]()
![]()
виконують рекурсивну часову фільтрацію за допомогою:
![]() ,
,
де
![]()
відповідає вектору зсуву ![]() в рядку та/або зсуву
в рядку та/або зсуву ![]() в стовпці, округлених до найближчих цілих чисел, між поточним зображенням
в стовпці, округлених до найближчих цілих чисел, між поточним зображенням ![]() і попереднім зображенням
і попереднім зображенням ![]() унаслідок поступального переміщення камери,
унаслідок поступального переміщення камери,
оновлюють матрицю ![]() нормування за допомогою:
нормування за допомогою:
![]()
і нормують вихід часового фільтра за допомогою:
![]() .
.
20. Машинозчитувальний носій запису, який зберігає комп'ютерну програму, що містить команди для реалізації способу за будь-яким з пп. 1-19 при виконанні програми процесором (PROC).
21. Пристрій обробки даних зображення, що містить вхід для обробки послідовних цифрових даних зображення, отриманих камерою, зануреною в рідину, яка містить явища турбулентності, що викликають ефект видимого зсуву пікселів зображень, який відрізняється тим, що додатково містить засіб обчислення для реалізації способу за будь-яким з пп. 1-19.
22. Застосування способу за будь-яким з пп. 1-19 для обробки даних зображення, що отримуються камерою, зануреною у воду в ядерній установці для зйомки збірок паливних елементів, яке відрізняється тим, що визначають з отриманих і оброблених зображень стан збірок паливних елементів.
23. Застосування за п. 22, яке відрізняється тим, що визначають на зазначених отриманих і оброблених зображеннях принаймні один ідентифікатор збірки паливного елемента.
24. Застосування за п. 22 або 23, який відрізняється тим, що додатково вимірюють на зазначених зображеннях інтервал між збірками паливних елементів.
25. Установка для реалізації застосування за будь-яким з пп. 22-24, яка відрізняється тим, що містить принаймні одну камеру і один пристрій за п. 21.
Текст
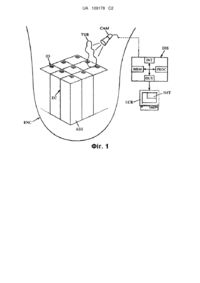
Реферат: Винахід належить до обробки даних послідовних цифрових зображень, отриманих камерою, зануреною в рідину, що містить турбулентність, таку як вода в активній зоні ядерного реактора, причому турбулентність викликає ефект зсуву пікселів зображень. Обробка переважно містить етапи, на яких: моделюють ефект турбулентності на пікселях зображень і виконують зворотну згортці за допомогою модельованого усередненого за часом зображення. UA 109178 C2 (12) UA 109178 C2 UA 109178 C2 5 10 15 20 25 30 Винахід стосується обробки цифрових даних зображення. Він, зокрема, направлений на обробку послідовних зображень (зазвичай послідовності у вигляді фільму). Такі зображення отримують за допомогою камери і, зокрема, камера занурена в рідину, в якій присутня турбулентність. Наприклад, такі ефекти турбулентності можуть виникати, через неоднорідності в рідкому середовищі, такі, як локальні різниці температури. Такі явища турбулентності викликають ефект видимого зсуву пікселів зображень. Наприклад, локальна відмінність в температурі в області, відповідній кромці зображення, призводить до явищ турбулентності, вплив яких на зняті на плівку зображення проявляє себе, як порушення порядку пікселів на кромці зображення з видимим зсувом (відносно початкового положення) деяких з цих пікселів, такий зсув змінюється з часом (випадковим чином). Випадкова природа таких змін призводить до труднощів (або навіть неможливості) при обробці зображень, для видалення ефектів турбулентності з них. Даний винахід направлений на поліпшення ситуації. З цією метою, в ньому запропонований спосіб для обробки даних зображення згаданого вище типу, що містить, зокрема етапи, на яких: - моделюють ефект турбулентності на пікселях зображень, та - виконують обернення згортки за допомогою згаданого моделювання для усередненого за часом зображення. Переважно, дійсно спостерігалося, що можливо ідеально змоделювати ефект турбулентності, але протягом відносно тривалого періоду. Таким чином, усереднювання пікселів зображення з часом дозволяє "подавити" вплив турбулентності. При цьому отримують усереднене, розмите зображення. Для того, щоб додати цьому зображенню різкість, до нього застосовують обернену згортку з використанням моделі, що представляє ефекти турбулентності. Звичайно, передбачається, що сцена, що знімається за допомогою камери, є фіксованою, хоча представлений нижче один варіант здійснення справжнього опису відноситься до випадку камери, яка поступально переміщається відносно статичної сцени. У одному переважному варіанті здійснення згадане вище моделювання ефектів турбулентності містить оцінку моделі h(u) щільності вірогідності для вектора u зсуву, що відноситься до ефекту турбулентності. Зокрема, спостерігалося, що, особливо переважно, імовірнісне моделювання впливу турбулентності на пікселях зображень дозволяло ідеально вирішувати проблему моделювання раніше випадкової турбулентності. Одним прикладом переважної моделі є тип, що експоненціально зменшується, і може бути виражений, як функція вектора u за допомогою рівняння наступного типу: 35 hu 40 45 Bu exp 2 55 де: представляє середньоквадратичне відхилення від норми вектора u A і B є позитивними речовими константами, такими, що, наприклад A 3 / і B 6 . Інші варіанти здійснення можливі і будуть описані нижче. У тому, що стосується оцінки усередненого за часом зображення, в одному можливому варіанті здійснення, включено середнє зважування на ступені фактора забування (нижче позначений, як ), з відповідним зменшенням функції за часом. Усереднене зображення I x, n , оцінка якого була виконана у час n для пікселя з координатами х вектора, може бути задане таким чином: I x, n 50 A 1 n1 n k 0 1 k Iх, n k член є дійсним числом, відповідним фактору забування. На практиці усереднене за часом зображення може бути оцінене, використовуючи рекурсивну часову фільтрацію. Таким чином, n-тий вихід часового фільтру для часу n, позначений, як I f x, n , і усереднене зображення I x, n зв'язані між собою рівняннями: I f x, n I f x, n 1 1 x, n I 1 UA 109178 C2 I x, n 5 10 I f x, n 1 n Виконані тести показали, що фактор забування був якнайкращим, якщо він був близький до 1, але при цьому все ще менше 1. Вибране значення, рівне 0,99, давало добрі результати. Далі, що стосується оберненої згортки, виконуваної при моделюванні, застосування лінійної просторової фільтрації, переважно, включене з виразом, відповідним згаданому вище моделюванню. Просторова фільтрація, переважно, може бути фільтрацією типу Вінера, хоча можливі інші варіанти здійснення. Просторовий фільтр заданий, наприклад, в спектральному домені виразом наступного типу: 1 H * f якщо f f c S b f 2 H f S sharp f W f W f 0, якщо f fc 15 20 25 де: - f є двовимірним вектором двох частот, нормованим після двовимірного перетворення Фур'є, - fc є частотою відсічення фільтру для усунення будь-якої потенційної спектральної ступінчастості, Sb f та S sharp (f ) , відповідно, є спектральні щільності потужності шумів та різкого зображення, що підлягають визначенню, та - H f є двовимірним перетворенням Фур'є щільності вірогідності ефекту турбулентності h(u). Спрощення цього виразу означало врахування просторового фільтру відповідно до виразу наступного типу: W ( f ) 30 f RBS де член RBS виражений як функція параметрів, вибраних таким чином, що член RBS -2 -4 знаходиться в діапазоні від 10 до 10 . Для співвідношення згаданого вище типу: h u 35 H f H2 Bu exp 2 A , двовимірне перетворення Фур'є H f щільності вірогідності впливу турбулентності H u , задано таким чином: H f 1 C(. f ) 2 3 2 40 де C є позитивною речовою константою, а є позитивним дійсним числом, що підраховується кількістю пікселів. Використовуючи значення констант A і B, що задані раніше і повністю визначають двовимірне перетворення Фур'є H f , це може бути потім представлене таким чином: 45 2 UA 109178 C2 2 H f 1 ( . f ) 2 3 5 10 15 3 2 Зокрема, виконані тести показали, що член переважно вибирати в діапазоні від 0 до 30 пікселів. Як згадано вище, даний винахід надає варіант здійснення, в якому камера може бути зміщена і може поступально переміщатися відносно статичної сцени. У такому разі представлена вище обробка може бути збережена, проте, потрібно виконати заходи по застосуванню зміни положення пікселів зображення у момент часу n-1 до наступного зображення у момент часу n, з подальшим урахуванням швидкості зсуву камери. Таким чином, в даному варіанті здійснення, зміну положення попереднього зображення відносно поточного зображення виконують для оцінки усередненого зображення. Рекурсивну часову фільтрацію потім виконують при зміні положення та нормуванні і, в одному зразковому варіанті здійснення, загальна обробка містить наступні етапи: - для скидання при: I f x,1 0 Nx,1 0 - для рекурсивної часової фільтрації при: 20 I f x, n 1 x, n I f x [ n,n1], n 1, I де [n,n1] [x n,n1],[y n,n1] 25 30 відповідає вектору для зсуву x в ряду, та/або зсуву y в стовпці, округлених до найближчих цілих чисел, між поточним зображенням n і попереднім зображенням n 1, унаслідок поступального переміщення камери - для оновлення матриці N нормування при: Nx, n 1 1 Nx [ n,n1], n 1 - і для нормування виходу часового фільтру, при: Im x, n 1 I f x, n Nx, n 35 40 45 50 55 Даний винахід також направлений на комп'ютерну програму, що містить команди для реалізації способу, представленого вище, коли ця програма виконується за допомогою процесора. Один приклад блок-схеми послідовності операцій загального алгоритму такої програми показаний на Фіг. 3, яка буде детально описана нижче. Даний винахід також направлений на пристрій для обробки даних зображення, що містить вхід для обробки послідовних цифрових даних зображення, отриманих камерою, зануреною в рідину, яка містить явища турбулентності, що викликають ефект видимого зсуву пікселів зображень. Зокрема, такий пристрій додатково містить засіб обчислення, призначений для реалізації способу, представленого вище. Такий засіб розрахунку може включати процесор і робочий засіб зберігання даних для виконання, наприклад, інструкцій згаданої вище комп'ютерної програми. Даний винахід, переважно, застосовний, але не обмежений цим, до обробки даних зображення, що отримуються камерою, зануреною у воду в ядерних установках, для зйомки збірок паливних елементів. Таке застосування способу за винаходом, в цьому контексті, може потім містити принаймні наступний етап: - визначають на основі отриманих і оброблених зображень стан збірок паливних елементів. Наприклад, в отриманих і оброблених зображеннях може бути визначений, принаймні, один ідентифікатор збірки паливного елементу. Варіант здійснення переважно представляє компоновку збірок усередині активної зони ядерного реактора, яку потрібно відстежувати і перевіряти. 3 UA 109178 C2 5 10 15 20 25 30 35 40 45 50 55 60 Застосування способу, в сенсі винаходу, може, крім того, містити етап, на якому: - вимірюють на згаданих зображеннях проміжок між збірками паливних елементів. Такий варіант здійснення, переважно, забезпечує можливість точного відстежування і перевірки відповідних положень збірок усередині активної зони. Зрештою, слід розуміти, що здійснення способу справжнього винаходу в рамках такого застосування дозволяє виконувати загальну інспекцію стану збірок, як у воді резервуару реактора, так і в залі реактора або в басейні витримки паливного залу. Даний винахід також направлений на установку для реалізації такого застосування, що містить принаймні одну камеру, переважно, водонепроникну і стійку до дії випромінювання, сполучену з пристроєм згаданого вище типу для реалізації винаходу. Інші переваги і властивості винаходу будуть зрозумілі при читанні докладного опису представлених нижче необмежувальних зразкових варіантів здійснення і також при прогляданні прикладених креслень, на яких: - на Фіг. 1 схематично показана зона реактора в рамках однієї реалізації відповідно до винаходу, разом з установкою, що містить камеру і пристрій для здійснення винаходу; - на Фіг. 2 схематично показані етапи способу в одному варіанті здійснення винаходу, з підтримкою зображень, як необроблених, так і оброблених, з використанням варіанту здійснення винаходу; - на Фіг. 3 показана блок-схема послідовності операцій етапів способу в одному варіанті здійснення, де камера виконує поступальне переміщення; - на Фіг. 4 показано різке зображення, отримане після використання способу, етапи якого представлені на Фіг. 3. Перш за все, буде зроблено посилання на Фіг. 1, на якій активна зона реактора в резервуарі ENC, заповненому водою, містить множину збірок ASS ядерних паливних елементів (кожна з яких, наприклад, зазвичай містить множину паливних стрижнів). Кожна збірка ASS містить ідентифікатор ID (оточений білим кругом у вигляді на Фіг. 4), і збірки розташовані через проміжок з використанням роздільників ЄС між збірками. Потім передбачена камера CAM, яка знімає збірки ASS і, зокрема, область, звану "S отворами" між такими збірками (не показані на Фіг. 1) та/або, принаймні, один ідентифікатор ID збірки. Зображення, отримані за допомогою камери, потім дозволяють: - наприклад, для S отворів, ідентифікувати деформацію отвору в межах часу використання, для зменшення ризику захоплення збірок паливних вузлів на штифтах, використовуваних для стабілізації збірок, та - зчитувати ідентифікатор збірки для забезпечення того, що кожна збірка паливних елементів знаходиться в місцеположенні, зазначеному в заданому плані активної зони. Такі зображення знімають за допомогою камери CAM, зануреної у воду, в яку занурені збірки. Унаслідок різниці температур у воді на місці (в результаті локальних варіацій показника заломлення води), може виникати явище TUR оптичної турбулентності. Даний винахід забезпечує моделювання турбулентності, що впливає на зображення, і використовує цю модель турбулентності, для обробки отриманих зображень. Один переважний варіант здійснення дозволяє поступально переміщати камеру, яка знімає ці зображення для обробки, зокрема, використовуючи технологію для зміни положення зображення, яке адаптоване до швидкості поступального переміщення. І знову, з посиланням на Фіг. 1, камера CAM сполучена з пристроєм DIS для обробки отримуваних зображень, що зазвичай містить: - інтерфейс INT, призначений для прийому отриманих даних зображення, - процесор PROC і робочий накопичувач MEM для обробки цих даних зображення, - вихідний інтерфейс OUT для попередньої обробки і передачі сигналу зображення на екран ECR, з подальшим відображенням оброблених зображень IMT (один приклад обробленого зображення показаний на Фіг. 4). Таким чином, використання способу, відповідно до даного винаходу, є переважним в контексті дистанційної відеоінспекції, зокрема, в кінці перезавантаження паливних елементів, яке в даний час складає важливий етап при операціях зупинки реактора для атомних електростанцій, що генерують електрику. Такі дистанційні відеоінспекції виконуються для перевірки плану активної зони (шляхом ідентифікації номерів збірок) і для точного визначення місцеположення цих збірок (наприклад, шляхом вимірювання зазорів між збірками). Дистанційні відео інспекції, крім того, наприклад, дозволяють перевіряти установку положення збірок. Спосіб також переважно застосовувати при обробці послідовності зображень (фотографій) для допомоги, зокрема, при розрахунку місць положення всіх або частини елементів збірок, але також і для інспекції стану цих збірок, наприклад, в паливному залі. 4 UA 109178 C2 5 10 15 20 25 30 35 Інтерпретація таких дистанційних відеоінспекцій часто пов'язана з труднощами, унаслідок вивільнення тепла з паливних елементів, що викликає явище турбулентності у воді. Для усунення таких труднощів була розроблена технологія для обробки знятих послідовностей зображення. Алгоритми для такої обробки були розроблені для роботи в режимі реального часу (отже, так, щоб вони дозволяли обробляти потік відеоданих, що безпосередньо знімався, кадр за кадром). У глобальному сенсі така обробка заснована на імовірнісному моделюванні дії турбулентності на пікселі зображень. Така модель турбулентності дозволяє визначити алгоритм обробки відновлення на двох етапах: - спочатку часова фільтрація дозволяє отримати стабільне, але розмите зображення (було показано, що таке розмите зображення відповідає згортці початкового різкого зображення (невідомо) з використанням лінійного просторового фільтру, вираз якого точно дорівнює щільності вірогідності вектора турбулентності); - друга фільтрація, яка виконується просторово, наприклад, за типом Вінера, дозволяє зробити початкове зображення різким (яке, таким чином, отримують, використовуючи лінійну обернену згортці). Обробка на цих двох етапах, описаних вище, застосовна, коли камера нерухома. Через час конвергенції часового фільтру, переважно, знерухомити камеру на декілька секунд перед отриманням задовільного відновленого зображення. У одному переважному варіанті здійснення потім передбачена технологія обробки зображень, коли камера рухається (зазвичай у вигляді поступального руху, відповідного найбільш частому випадку). У разі камери, що виконує поступальну ходу, передбачають етап (не обов'язковий, але переважний) зміни положення зображення для того, щоб забезпечити адаптацію часового фільтру до варіацій камери. Таку зміну положення зображення виконують шляхом попередньої оцінки рухи камери. Робочі характеристики є задовільними, переважно, без втрати якості відносно обробки з використанням статичної камери. Далі, як перший етап, буде описаний один приклад моделі деградації, через турбулентності. Нижче, Ix, n, c позначає значення пікселя з координатами х x, y у n-тому ряду отриманого зображення, для компоненту c c 12,3 с відповідно, для червоного, зеленого, , синього компонентів). Оскільки операції обробки ідентичні для всіх трьох компонентів, позначення спрощені так, що оброблювані компоненти не згадуються, і Ix, n, c просто записують, як Ix, n . У ідеальних умовах (відсутність турбулентності, статична камера, постійна сцена), зображення I(x, n), послідовності кадрів, що знімається, отримують в результаті вибірки одного і того ж різкого, оригінального і безперервного зображення, позначеного, як Isharp x , при Ix, n Isharp x . Потім вважається, що у присутності турбулентності кожен піксель зображення зміщується від його початкового положення. Позначаючи, як u x,n , вектор, відповідний зрушенню пікселя x на зображенні n, може бути записане наступне: 40 45 Ix, n Isharp x u x,n Зсуви, через турбулентність, крім того, є випадковими. Пошук аналітичного виразу для вектора u x,n зсуву, здається чимось, що не може бути представлене. Потім надають імовірнісний опис цих зсувів. Вектор u x,n турбулентності розглядають, як випадковий вектор, відповідно до певної щільності вірогідності, позначеної таким чином: h x,n u 50 На основі припущення, що явища турбулентності є стаціонарними, як за часом, так і в просторі (у разі рідкого середовища, такого як вода), можна розглядати, що щільність вірогідності не залежить ні від x, ні від n, і може бути записано наступне: h x,n u hu 55 де hu є щільністю вірогідності турбулентності для будь-якого заданого зображення n і для 5 UA 109178 C2 будь-якого заданого пікселя x . Представлені нижче операції обробки засновані на цій гіпотезі стаціонарності явищ турбулентності. Реально, при позначенні, як Im x, n , усереднене зображення за час n визначається таким чином: 5 Im x, n 10 1 n Ix, k n k 1 при цьому було показано, що це усереднене зображення сходиться у напрямку стабільного зображення Istable ( x) , яке дорівнює згортці початкового різкого зображення (невідомо) з наступною щільністю вірогідності турбулентності: Istable ( x) lim Im x, n Isharp h x n 15 20 25 Таким чином, для відновлення невідомого різкого зображення, усереднене зображення повинне бути піддане тільки оберненій згортці по щільності вірогідності турбулентності hu . Оскільки така щільність вірогідності не відома, нижче представлена емпірична модель для опису варіацій щільності вірогідності на основі двох наступних фізичних особливостей: - явища турбулентності, загалом, є ізотропними, і щільність вірогідності повинна бути незалежною від кута вектора u - малі зсуви пікселів виявляються частіше, ніж значні зсуви пікселів: таким чином, коли норма вектора u зменшується, значення hu повинне зменшитися. Інші фактори, звичайно, можуть бути розглянуті при виборі моделі. Наприклад, може бути практичним розмістити аналітичний вираз, параметри якого регулюються для hu , і, зокрема, для його перетворення Фур'є. Проста модель, яка перевіряє всі такі гіпотези, є моделлю типу, що експоненціально знижується, такою як, наприклад: h u 30 35 40 exp 2 3 У цій формулі представляє середньоквадратичне відхилення (середнє відхилення) норми вектора турбулентності. Цей параметр дозволяє враховувати відмінності рівня турбулентності, відповідно до знятих послідовностей кадрів. Як варіант, можна використовувати Гаусову модель. Проте, тести з експоненціальною моделлю показали добрі результати. Інші типи моделей, що проявляють менше зниження, ніж Гаусове, або експоненціальні моделі, звичайно, можуть бути розглянуті, як додаткові варіанти. Потім можливо виконати оцінку оригінального зображення на двох етапах обробки. На першому етапі, послідовність необроблених зображень усереднюють за часом. Таке усереднене зображення сходиться до стабільного зображення Istable x , яке рівне згортці невідомого різкого зображення (яке могло б спостерігатися за відсутності явищ турбулентності) з щільністю вірогідності турбулентності, при: 50 Istable x lim Im x, n Isharp h x n 45 6u Обернена згортка усередненого зображення по щільності вірогідності турбулентності потім, на другому етапі, дозволяє виконати оцінку оригінального різкого зображення. На Фіг. 2 ілюструються два основні етапи обробки реальних зображень збірок. Перший (часовий) фільтр F1 дозволяє отримати усереднене, стабільне, але розмите зображення ISF, починаючи з послідовності зображень IMn, IMn1, і так далі. Другий (оберненої просторової згортки) фільтр F2, дозволяє відновити початкове різке зображення IN, починаючи з розмитого зображення ISF. Часова фільтрація F1 буде описана нижче. Якщо знята сцена є постійною (ігноруючи ефекти турбулентності), зокрема, в тому, що стосується освітлення, коефіцієнта збільшення і так далі, n-те усереднене зображення 6 UA 109178 C2 отримують за наступною формулою: Im x, n 5 10 1 n Ix, k n k 1 У цій формулі одну і ту ж вагу призначають для кожного зображення. Для обробки будь-яких потенційних варіацій сцени (освітлення та інших), переважно призначати, для усередненого зображення, більшу вагу для останніх зображень, ніж для минулих зображень. Для середнього зображення у момент часу n, зображення I x, n знімають на основі наступного: I x, n 1 n1 n k 0 1 k Iх, n k Член є фактором забування, який дозволяє призначати великий або менший ступінь важливості для минулих зображень (як пам'ять передісторії фільтру). Нормалізація по членові 15 1 1 n дозволяє отримати геометричну суму вагів k , рівну 1, оскільки: 1 n1 n k 0 1 20 25 k Формула I x, n може набувати форми рекурсивної часової фільтрації, після якої слідує етап нормалізації. N-тий вихід часового фільтру, позначений, як Ix, n , і нормалізованого вихідного зображення, позначеного, як I x, n , потім зв'язують наступним: I f x, n I f x, n 1 1 x, n I I x, n 30 1 I f x, n 1 1 n Значення, вибране для фактора забування, визначає робочі характеристики часового фільтру. Для оцінки таких робочих характеристик, визначають середню квадратичну різницю між пікселем x n-ого зображення і пікселем x цільового стабільного зображення таким чином: Г 2 x, n E I x, n Istable x 2 35 Потім можливо визначити середньоквадратичну різницю для всього зображення n: Г 2 n 1 Г 2 x, n Npixels x У разі постійної сцени, ігноруючи ефекти турбулентності, було показано наступне: 40 Г 2 n 1 1 1 1 2n 2 n 2 2 45 де Σ є середнім відхиленням пікселів n в необробленому зображенні. Після конвергенції (коли n прагне до нескінченності), залишкова квадратична різниця нормалізованого виходу часового фільтру визначається таким чином: 7 UA 109178 C2 Г 2 5 10 1 2 1 Розрахунки згортки середньоквадратичного відхилення, як функції кількості оброблених зображень, для різних значень фактора забування, показують, що у разі статичної сцени, переважно, вибрати , як можна більшим. Проте, у разі змінної сцени, вибір фактора забування виконують на основі компромісу між коротким часом для адаптації до зміни сцени (мале значення ) і малим залишковим середньоквадратичним відхиленням (велике значення ). Якщо, наприклад, виникає різка зміна сцени (наприклад, зміна освітлення) у момент часу n 0 , тоді як для часового фільтру було виконано сходження, було показано, що середньоквадратичне відхилення між виходом фільтру у момент часу n і стабільним зображенням стає: Г 2 n 1 2 2(nn ) 2 1 0 15 20 25 30 35 де Δ представляє середнє відхилення рівня, викликане зміною сцени. Таким чином, чим більше значення фактора забування, тим більший час конвергенції буде отриманий (приблизно 300 зображень або 12 секунд для 0,99 ), але залишкове середньоквадратичне відхилення при цьому є достатньо малим (0,07 для 0,99 ) для вихідного зображення, яке повинне володіти можливістю стабілізації. При зменшенні вибраного значення підвищується швидкість сходження (приблизно 50 зображень, або 2 секунди, для 0,95 ), але залишкове середньоквадратичне відхилення також збільшується (0,16 для 0,95 ). Вихідне зображення не буде повністю стабілізоване, навіть після сходження. У одному поточному варіанті здійснення фактор забування, переважно, встановлений, як 0,99, що є оптимальним значенням, у разі постійної сцени (ігноруючи ефекти турбулентності). Проте, представлена тут обробка, є достатньо гнучкою для адаптації до частих змін сцени, що знімається (зазвичай зміни освітлення). Зокрема, у разі рухомої камери (представленої нижче), кожен елемент сцени є видимим тільки на зменшеній кількості зображень. При цьому переважно зменшити фактор забування для того, щоб призначити більшу значущість для часу конвергенції, ніж для залишкової розбіжності. Просторова фільтрація, використовувана на другому етапі способу, буде описана нижче в одному зразковому варіанті здійснення. Відповідно до моделі деградації, описаної вище, нормалізований вихід, I x, n стає рівним стабільному зображенню Istable x (згортка невідомого різкого зображення з щільністю вірогідності, відповідній турбулентності), для якого додають шум bx, n з середнім відхиленням, заданим по: Г 2 n 1 1 1 1 2n 2 n 2 40 яке може бути записане, як: x, n Isharp h x bx, n I 45 Оцінка різкого зображення, що починається з виводу I x, n , тому, зводиться до проблеми лінійної просторової оберненої згортки. Оптимальний фільтр відновлення заданий по формулі Вінера, яка в спектральному домені є: 8 UA 109178 C2 W f H * f , якщо f f c S b f 2 H f S sharp f Wf 0, якщо f fc 5 10 15 20 де: - f є двовимірним вектором f f, g двох нормалізованих частот після 2-D перетворення Фур'є, - fc є частотою зрізу фільтру, що дозволяє виключити будь-який потенційний спектральний аналіз вхідних зображень, - Sb f і S sharp f , відповідно, є спектральна щільність потужності шумів і різкого зображення, яке повинне бути відновлене, і - H f є 2-D перетворенням Фур'є від h(u). У експоненціальній моделі, вибраній для h(u), тоді: 2 H f TF2D h u 1 f 3 30 На першому етапі зроблено припущення, що шуми і зображення мають постійну спектральну щільність потужності (зображення і білого шуму, S b(f) і Ssharp(f) є константами). Враховуючи, що перетворення Фур'є щільності вірогідності є речовим, оптимальний фільтр для відновлення зображень може бути визначений за наступною формулою: W f 25 3 2 2 H f 2 H ( f ) RBS Тут член RBS, що позначає "Відношення сигнал-шум", відповідає відношенню між потужністю шумів на виході часового фільтру і потужністю різкого зображення (невідомо). Такий фільтр відновлення містить два параметри: RBS і . Ці два параметри впливають на частотний відгук фільтру. Для отримання порядку магнітуди для RBS можна розглянути, що різке зображення (невідомо) має значення пікселів, відносно рівномірно розподілені в діапазоні P. 2 Показано, що дисперсія значень, прийнятих по пікселях, складає потім P /12. Після конвергенції часового фільтру залишкова дисперсія на виході рівна 1 / 1 2 , де 2 є дисперсією шумів необроблених зображень, і є фактором забування фільтру. Таким чином, для відношення RBS: 1 2 2 1 1 RBS 12 P2 1 P 12 35 40 45 Наприклад, для відношення "шуми/діапазон зображень", перед обробкою, -4 / P 0, 1Σ/P=0,1, і при факторі забування 0,99 , набувають значення RBS, рівного 6·10 . Цей результат представляє порядок магнітуди оптимального значення RBS. Відношення RBS може бути фіксоване емпірично, відповідно до різних тестів над оброблюваними зображеннями. Як правило, виявляється, що, коли RBS прагне до 0, фільтр обернення згортки проявляє тенденцію перетворення на інверсний фільтр 1/ Hf , що пропускає верхні частоти і чутливий до шуму. Значення, яке дуже мале для RBS тому, дає зашумлені відновлені зображення ("зернистий" шум, спостережуваний в оброблених зображеннях). Якщо RBS прагне до нескінченності, фільтр обернення згортки прагне до фільтру Hf розмитості. Дуже високе значення для RBS, тому, призводить до розмитого відновленого 9 UA 109178 C2 -4 5 10 15 20 Ia x, n 25 -2 зображення. Оптимальне значення для RBS знаходиться, відповідно до тестів, між 10 і 10 , -3 таким чином, що було вибрано набутого за умовчанням значення 10 . Параметр дозволяє прийняти параметри фільтру відновлення, як середньоквадратичне відхилення (середнє відхилення) ефектів турбулентності. Як правило, якщо менше, ніж реальне середньоквадратичне відхилення ефектів турбулентності, розмитість зображення після фільтрації за часом (на вході просторового фільтру) не буде повністю усунена. Якщо більше, ніж реальне середньоквадратичне відхилення ефектів турбулентності, високі частоти зображення будуть дуже сильно посилені, і якість зображення буде погіршено. Оптимальне значення строго залежить від рівня ефекту турбулентності і коефіцієнта збільшення (ефект турбулентності, погіршуючий послідовність відеозображень більшою мірою, коли коефіцієнт збільшення є великим). Один приклад оптимального значення для знаходиться в області 8 пікселів для низьких рівнів турбулентності. На відміну від цього, для високих рівнів турбулентності при великому коефіцієнті збільшення оптимальне значення для складає приблизно 30 пікселів. Потім слід розуміти, що значення може бути вибрано між 0 і 30 пікселями. Цей параметр може оновлюватися, у міру отримання зображення, під час операцій по обробці і залежно від якості отримуваних зображень. Нижче буде описаний один варіант здійснення, в якому враховується переміщення камери, що знімає зображення. Представлена вище обробка полягала в оберненій згортці нормалізованих вихідних даних з часового фільтру, заданій за наступною формулою: 1 1 n n nk Ix, k k 1 Проте, таке середнє значення, представлене вище, більше не має сенсу, якщо камера рухається, і якщо необроблені зображення зрушуються відносно один одного. У разі лінійної камери, що переміщається, кожне зображення k зрушується на певний вектор n,k відносно поточного зображення n . Якщо положення кожного зображення буде змінене, як функція його переміщення, представлена вище формула набуває наступної форми: 30 35 Ia x, n 1 1 n( x ) n nk I x nk , k ~ k nn( x )1 nk x nk , y nk є вектором для зсуву стовпця (уподовж x) і ряду (уподовж у) між зображенням k і зображенням n, і n( x ) позначає кількість послідовних зображень, що містять піксель x після зміни положення. Вираз: ~ I x nk , k 40 45 є інтерполяцією необробленого зображення в x nk . Як і у разі відновлення статичної камери, середнє зображення може набувати форми рекурсивного фільтру, після якого слідує нормалізація. Нормалізація тут виконується складніше, ніж у разі статичної камери, оскільки кількість доступних зображень залежить від області даного зображення (нормалізація по пікселю). Проте, показано, що вона може бути виражена таким чином: I x, n 50 ~ I f ( x, n) 1 x, n If x n,n1 , n 1 , I 1 1 n( x ) I f x, n . Ці вирази, тому, мають на увазі використання інтерполяції попередніх вихідних даних фільтру (час n-1). Для виключення операцій інтерполяції, які є дорогими в сенсі потужності обробки, 10 UA 109178 C2 вибирають наступне спрощення рівняння фільтрації: If ( x, n) 1 x, n I f x n,n1 , n 1 , I I x, n 5 I f x, n . 1 n( x ) У цьому виразі, вектор зсуву в рядку і в стовпці, округлений до найближчих цілих чисел, між поточним зображенням n і попереднім зображенням n-1, позначений таким чином: 1 n,n1 xn,n1y n,n1 . , 10 При цьому показано, що розраховують тільки одну матрицю нормалізації для кожного пікселя: Nx, n 1 n( x ) 15 20 шляхом розрахунку виходу часового фільтру із зміненим положенням, коли постійне зображення, рівне 1, встановлюють на вході поверх всіх пікселів. Повна операція часової фільтрації із зміною положення і нормалізацією зрештою може бути записана відповідно до чотирьох етапів: - скидання: If ( x,1) 0 Nx,1 0, - часова фільтрація: If ( x, n) 1 x, n I f x n,n1 , n 1 I - оновлення нормалізованої матриці: Nx, n 1 1 N x n,n1 n 1 - нормалізація виходу часового фільтру: 25 Im x, n 30 35 40 45 1 I f x, n N( x, n) Таким чином, у міру прийому кожного зображення: - на першому етапі оцінюють зсуву n,n1 між поточним зображенням n і попереднім зображенням n 1, - цей зсув використовують для зміни положення часового фільтру і - для розрахунку матриці нормалізації для кожного пікселя, - потім нормалізований вихід з часового фільтру піддають оберненій згортці, використовуючи просторовий фільтр. Спосіб оберненої згортки є таким, як, описано вище для випадку статичної камери. Нижче описана оцінка послідовного переміщення між двома зображеннями. Декілька типів підходів існують для оцінки зсуву між різними зображеннями. Прості технології є тут переважними, так, щоб забезпечити можливість виконання операції обробки в режимі реального часу. Найпростіший підхід полягає в пошуку максимальної взаємної кореляції між зображеннями. З тим, щоб виключити чутливість до шумів, до ефектів турбулентності і варіацій освітлення, переважно працювати не з самими зображеннями, але з контурами зображення. Оцінка зсуву між двома зображеннями, таким чином, складається з двох етапів. На першому етапі два "контурні" зображення отримують шляхом фільтрації початкових зображень. На другому етапі розраховують матрицю взаємної кореляції між двома зображеннями. Координати максимуму взаємної кореляції позначають зсуву рядка і стовпця між цими двома зображеннями. Фільтр, що забезпечує можливість отримання зображення контурів, є фільтром Собеля, визначеним таким чином: 50 x2 exp 3 2 2. Sobel 2 Sobel де Sobel управляє смугою пропускання фільтру, і MSobel є розміром вікна фільтрації. x MSobel MSobel : Sobel( x ) x 11 UA 109178 C2 Переважні значення цих параметрів є Sobel 0,9 пікселів, MSobel 5 Sobel . Один і той же фільтр використовується для фільтрації рядів і стовпців зображення I(x, у), з тим, щоб отримати контурне зображення, позначене, як Icontour x, y : I temp x, y MSobel Sobel(k ) Ix k, y k MSobel 5 Icontour x, y MSobel Sobel(k ) I temp x, y k k MSobel Взаємна кореляція між двома контурними зображеннями I1contour x, y і I2 contour x, y потім визначається за наступною формулою: 10 x, y I1contour x y 2 ( x, y )Icontour x x, y y Для істотного зменшення часу розрахунку, член: 15 x, y може бути отриманий шляхом використання швидкого перетворення Фур'є: 2 x, y IFFT FFT I1 contour x, y FFT Icontour Ncolumns x, Nrows y , 20 25 30 35 40 Для подальшого зменшення часу розрахунку, оцінку руху виконують тільки для одного каналу зображення. Може виникнути випадок, в якому ряди необроблених прийнятих зображень піддають обробці переміжності. При цьому переважно, в даному випадку, зберігати тільки кожен другий ряд (наприклад, парні ряди) в зображеннях з взаємною кореляцією. Нарешті, в певних випадках, послідовність відеозображень містить перезаписані дані (зазвичай дату і час, назву реактора, координати збірки, що знімається). При цьому, звичайно, рекомендується не використовувати цю область зображення для оцінки зсуву. Далі буде описаний розрахунок зміни положення. Для зміни положення послідовних виходів часового фільтру між двома зображеннями, перше рішення полягає в розрахунку, в кожен момент часу n , величини зсуву n,n1 між поточним зображенням n і попереднім зображенням n 1. Проте, тести показали, що даний підхід не можна застосовувати у разі (що часто виникає) повільного руху камери. Це можна пояснити таким чином: припустимо, наприклад, що рух камери призводить до зсуву на 0,3 ряду для кожного зображення і до нульового зсуву вниз по стовпцю, при цьому матриця кореляції між двома послідовними зображеннями, загалом, стає максимальною при n,n1 0, 0,3 0,0 . Таким чином, зсув не може бути детектований, і зміна положення зображення не виконується, тоді як рух камери, проте, вимагає реальної зміни положення приблизно на 3 ряди для кожних десяти зображень. Для того, щоб мати можливість відстежувати повільні зсуви (зазвичай менше, ніж 0,5 рядів або стовпців на зображення), нижче представлений інший підхід. Величину зсуву оцінюють не між поточним зображенням n і попереднім зображенням n 1, але між поточним зображенням n і опорним зображенням n,ref . Член n,n1 потім просто визначають таким чином: 45 50 n,n1 n,ref n1,ref У таблиці 1, представленій нижче, ілюструється така обробка для випадку швидкості зміни 0,3 ряду на зображення. В даному прикладі реально оцінюють середнє з трьох зображень із зсувом для кожних 10 зображень. Опорне зображення оновлюють, коли поточне зображення отримало істотний зсув. Порогове значення 20 пікселів максимального зсуву було фіксовано, що дозволяє управляти будь-яким рухом камери з швидкістю вище, ніж 1/20 (або 0,05 12 UA 109178 C2 рядів/стовпців на зображення), що, у свою чергу, виявляється достатнім для випадку даних варіантів додатків. Таблиця 1 Індекс зображення nref nref +1 nref +2 nref +3 nref +4 nref +5 nref +6 nref +7 nref +8 nref +9 nref +10 Реальний зсув поточного зображення/ 0 0,3 0,6 0,9 1,2 1,5 1,8 2,1 2,4 2,7 3 опорного зображення y n,ref Оцінка зсуву поточного зображення/ опорного зображення 0 0 1 1 1 2 2 2 2 3 3 0 1 0 0 1 0 0 0 1 0 [y n,ref ] Оцінка зсуву поточного зображення/ опорного зображення n,n 1 [y n,ref ] [y n 1,ref ] 5 10 15 20 25 30 35 На Фіг. 3 узагальнені різні етапи обробки зображень в ситуації з рухом, в якій: - при використанні поточного зображення IMn час n , на етапі S1, виконують оцінку зсуву, і, у разі, коли оцінка зсуву на етапі S1 перевищує порогове значення (тест S6), виконують оновлення порогового значення на етапі S7, - на етапі S2 розраховують зміну положення, - часова фільтрація на етапі S3 і нормалізації по пікселю на етапі S4, та - просторова фільтрація в етапі S5 для отримання різкого зображення IN. Робочі характеристики обробки є задовільними, при цьому відсутня втрата якості відносно обробки, в якій використовується статична камера. Деякі штучні спотворення зображення, проте, можуть з'являтися, коли камера починає рух після її перебування в стані спокою протягом декількох секунд. Ці штучні спотворення, проте, не є функціонально проблематичними. Як показано на Фіг. 4, такі штучні спотворення (ряд, позначений чорною стрілкою на даній фігурі), не перешкоджають ні зчитуванню номера збірки (усередині білого круга, в якому записаний номер "2D EL"), ні розрахунку проміжку між збірками (подвійна біла стрілка). Крім того, ці штучні спотворення можуть бути зменшені, використовуючи прості технології обробки зображень. Само собою зрозуміло, що даний винахід не обмежений описаними вище, як приклад, варіантами здійснення; він може бути розширений на інші варіанти. У представленому вище прикладі, часовий фільтр виконує просте усереднювання послідовних зображень відеопослідовності. При такому усереднюванні може бути включене призначення більшої ваги (або відповідно, меншої ваги) для зображень з хорошою (відносно поганим) якістю. У більш загальному випадку, часовий фільтр може бути замінений операціями по обробці для комбінування більш відповідних зображень. Такі підходи мають на увазі, проте визначення одне або більше індикаторів якості, розрахованих по області, що представляє інтерес, для зображень (області, що містять номер збірки). Просторовий фільтр, представлений вище, працює по всьому зображенню. Як варіант, може бути передбачена можливість концентрації обробки в області, що представляє інтерес. Зокрема, "заздалегідь відома" інформація, така як двійкова природа області, що містить число, може враховуватися при обробці відновлення. Крім того, поточний просторовий фільтр виконує обернення згортки Вінера для всього зображення. Інші технології обробки обернення згортки, використовуючи, наприклад, вейвлетперетворення, можуть використовуватися в рівній мірі. Крім того, слід зазначити, що технології для поліпшення контрасту шляхом локального вирівнювання гістограм для вирівнювання контрасту можуть бути переважними. 40 13 UA 109178 C2 ФОРМУЛА ВИНАХОДУ 5 10 15 20 25 1. Спосіб обробки послідовних цифрових даних зображення, отриманих за допомогою камери, зануреної в рідину, що містить явища турбулентності, які викликають ефект видимого зсуву пікселів зображень, що містить етапи, на яких: моделюють ефект турбулентності на пікселях зображень, та виконують обернення згортки за допомогою згаданого моделювання, усередненого за часом зображення. 2. Спосіб за п. 1, який відрізняється тим, що на етапі моделювання виконують оцінку моделі щільності вірогідності вектора u зсуву, що належить до ефекту турбулентності. 3. Спосіб за п. 2, який відрізняється тим, що згадана модель належить до типу з експоненціальним зменшенням. 4. Спосіб за п. 3, який відрізняється тим, що згадана модель h (u) виражена як функція вектора u рівнянням вигляду: A Bu h (u) 2 exp , де: - середньоквадратичне відхилення норми вектора u , A і B - позитивні речові константи. 5. Спосіб за п. 4, який відрізняється тим, що A 3 / і B 6 . 6. Спосіб за будь-яким з пп. 1-5, який відрізняється тим, що усереднене за часом зображення оцінюють по середньому значенню, зваженому по ступенях фактора забування, що відповідно зменшується залежно від часу. 7. Спосіб за п. 6, який відрізняється тим, що середнє зображення I ( x, n) , що оцінюється у час n для пікселя з векторними координатами x , визначається наступним чином: 30 1 n 1 kI( x,n k ) , 1 n k 0 де член є дійсним числом, відповідним фактору забування. 8. Спосіб за будь-яким з пп. 1-7, який відрізняється тим, що усереднене за часом зображення оцінюють з використанням рекурсивної часової фільтрації. 9. Спосіб за п. 8, який відрізняється тим, що n-ий вихід часового фільтра для моменту часу n , позначений як I ( x, n) , і середнє зображення I ( x, n) зв'язані між собою рівняннями: I( x, n) If ( x,n) If ( x,n 1) (1 )I( x,n) , I ( x, n) 35 40 If ( x,n) . 1 n 10. Спосіб за будь-яким з пп. 6, 7 та 9, який відрізняється тим, що фактор забування вибирають рівним 0,99. 11. Спосіб за будь-яким з пп. 1-10, який відрізняється тим, що на етапі виконання обернення згортки застосовують лінійну просторову фільтрацію до виразу, відповідного згаданому моделюванню. 12. Спосіб за п. 11, який відрізняється тим, що фільтрація є фільтрацією типу Вінера. 13. Спосіб за п. 12, який відрізняється тим, що просторовий фільтр заданий в спектральній області наступними формулами: W ( f ) 45 1 H* ( f ) , якщо f fc , Sb ( f ) 2 H ( f ) Ssharp ( f ) W (f ) 0 , якщо f f c , де: f - двовимірний вектор двох частот, що нормуються після двовимірного перетворення Фур'є, f c - частота відсічення фільтра для усунення будь-якої потенційної спектральної ступінчастості, Sb ( f ) і Ssharp ( f ) - відповідно щільності спектральної потужності шумів та різкого зображення, що підлягає визначенню, та 14 UA 109178 C2 H ( f ) - двовимірне перетворення Фур'є щільності вірогідності ефекту турбулентності h (u) . 14. Спосіб за п. 13, який відрізняється тим, що просторовий фільтр виражений наступним рівнянням: H (f ) , W ( f ) 2 H ( f ) RBS 5 де член RBS виражений як функція параметрів, вибраних таким чином, що член RBS -2 -4 знаходиться в діапазоні від 10 до 10 . 15. Спосіб за будь-яким з пп. 13 або 14, який відрізняється тим, що двовимірне перетворення Фур'є H ( f ) щільності вірогідності ефекту турбулентності h (u) задане наступним рівнянням: H ( f ) 1 C( f )2 10 3 2 , де C - позитивна речова константа, а є позитивним дійсним числом, підрахованим за кількістю пікселів. 16. Спосіб за п. 15, який відрізняється тим, що двовимірне перетворення Фур'є H ( f ) визначається наступною формулою: 15 20 25 3 2 2 H ( f ) 1 ( f )2 , 3 де знаходиться в діапазоні від 0 до 30 пікселів. 17. Спосіб за будь-яким з пп. 1-16, який відрізняється тим, що згадана камера поступально переміщається, при цьому застосовують зміну положення попереднього зображення до поточного зображення для оцінки середнього зображення. 18. Спосіб за п. 17, який відрізняється тим, що додатково містить етап, на якому виконують часову фільтрацію із зміною положення та нормуванням. 19. Спосіб за п. 18, який відрізняється тим, що додатково містить етапи, на яких: виконують скидання за допомогою: If ( x,1) 0 , N( x,1) 0, виконують рекурсивну часову фільтрацію за допомогою: If ( x, n) (1 )I( x, n) I f ( x [n,n1], n 1) , де [n,n1] [xn,n1],[yn,n1] відповідає вектору зсуву x в рядку та/або зсуву y в стовпці, округлених до найближчих цілих 30 35 40 45 50 чисел, між поточним зображенням n і попереднім зображенням n 1 унаслідок поступального переміщення камери, оновлюють матрицю N нормування за допомогою: N( x,n) 1 1 Nx [n,n1],n 1 і нормують вихід часового фільтра за допомогою: 1 Im ( x, n) If ( x, n) . N( x, n) 20. Машинозчитувальний носій запису, який зберігає комп'ютерну програму, що містить команди для реалізації способу за будь-яким з пп. 1-19 при виконанні програми процесором (PROC). 21. Пристрій обробки даних зображення, що містить вхід для обробки послідовних цифрових даних зображення, отриманих камерою, зануреною в рідину, яка містить явища турбулентності, що викликають ефект видимого зсуву пікселів зображень, який відрізняється тим, що додатково містить засіб обчислення для реалізації способу за будь-яким з пп. 1-19. 22. Застосування способу за будь-яким з пп. 1-19 для обробки даних зображення, що отримуються камерою, зануреною у воду в ядерній установці для зйомки збірок паливних елементів, яке відрізняється тим, що визначають з отриманих і оброблених зображень стан збірок паливних елементів. 23. Застосування за п. 22, яке відрізняється тим, що визначають на зазначених отриманих і оброблених зображеннях принаймні один ідентифікатор збірки паливного елемента. 24. Застосування за п. 22 або 23, який відрізняється тим, що додатково вимірюють на зазначених зображеннях інтервал між збірками паливних елементів. 25. Установка для реалізації застосування за будь-яким з пп. 22-24, яка відрізняється тим, що містить принаймні одну камеру і один пристрій за п. 21. 15 UA 109178 C2 16 UA 109178 C2 Комп’ютерна верстка Л. Ціхановська Державна служба інтелектуальної власності України, вул. Василя Липківського, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут інтелектуальної власності”, вул. Глазунова, 1, м. Київ – 42, 01601 17
ДивитисяДодаткова інформація
Назва патенту англійськоюProcessing of image data comprising effects of turbulence in a liquid medium(fr) traitement de donnees d'images comportant des effets de turbulences dans un milieu liquide
Автори англійськоюPaul, Nicolas, de Chillaz, Antoine
Автори російськоюПоль Николя, дэ Шийяз Антуан
МПК / Мітки
МПК: G06T 5/50
Мітки: даних, зображення, результаті, містять, рідкому, середовищі, турбулентності, обробка
Код посилання
<a href="https://ua.patents.su/19-109178-obrobka-danikh-zobrazhennya-shho-mistyat-rezultati-turbulentnosti-u-ridkomu-seredovishhi.html" target="_blank" rel="follow" title="База патентів України">Обробка даних зображення, що містять результати турбулентності у рідкому середовищі</a>
Наступний патент: Тверда дозована лікарська форма та спосіб її одержання
Випадковий патент: Зубчасте колесо беззазорної передачі