Спосіб автоматичного регулювання об’єктом на основі обчислення векторної похибки автоматичного регулювання

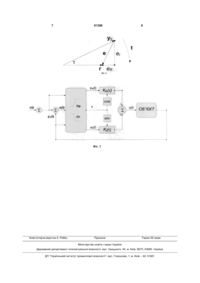
Спосіб автоматичного регулювання об'єктом регулювання на основі обчислення векторної похибки автоматичного регулювання, в якому вихідний сигнал об'єкта регулювання регулюють шляхом зміни сигналу на виході регулятора, який відрізняється тим, що вихідний сигнал об'єкта регулювання y визначають як вектор з врахуванням фазового (або часового) зсуву відносно сигналу на вході (або сигналу заданої уставки) об'єкта регулювання, визначають фазовий (або часовий) зсув вихідного сигналу об'єкта регулювання, та на вхід регулятора подають сигнал, який вибирають рів ним векторній похибці е, яку визначають як різницю між вектором сигналу уставки r, що є заданим значенням вихідного сигналу об'єкта регулювання, та вектором вихідного сигналу об'єкта регулювання y, і при цьому регулюють вихідний сигнал об'єкта регулювання на основі значень векторної похибки е регулятора, її дійсної eR та уявної eJ складових, які визначають відповідно до співвідношень: 1. Галузь техніки запропонованого винаходу. Запропонований на розгляд спосіб регулювання на основі векторної похибки належить до галузі техніки систем автоматичного регулювання (CAP) об'єктами, в тому числі нелінійними, довільного порядку, при наявності затримок та недостатній інформації для побудови точної математичної моделі об'єкту. 2. Рівень техніки. Існуючі системи автоматичного регулювання для своєї роботи повинні мати математичну модель об'єкту регулювання, на основі якої можливо досягти заданих характеристик та показників якості, які задаються цільовою функцією виду: e r y eR j eI ; e2 r2 y2 2 r y cos ; eR r y lim 1 T 2 u t 0T0 (r y )2 dt min, (1) де u - вихідний сигнал регулятора, r - задане значення вихідного сигналу об’єкта регулювання (уставка), y - визначений вихідний сигнал об'єкту регулювання, е=r-y - похибка регулювання, d збурення (зовнішнє або внутрішнє внаслідок зміни параметрів або структури об'єкту), у відповідності до Фіг.1. (19) G(u, e) UA (11) 1 - уявна одиниця; j = - фазовий зсув між вектором сигналу уставки r та вектором виміряного вихідного сигналу об'єкту автоматичного регулювання y. (13) де r - модуль вектора заданого значення вихідного сигналу об'єкта регулювання (уставки), відносно якого визначається фазовий зсув вихідного сигналу об'єкта автоматичного регулювання; y - модуль вектора вихідного сигналу об'єкта автоматичного регулювання; C2 y sin , 91398 eI cos ; 3 91398 Запропоновані на сучасний час різноманітні адаптивні системи автоматичного регулювання на основі нечіткої логіки, штучних нейронних мереж та інших методів, як свідчить практика, не знаходять широкого використання і у всіх галузях техніки, промисловості у більш ніж 90% випадків [1] використовується пропорційно-інтегральнодиференційний (ПІД) регулятор або його різновиди П, ПІ, ПД. Аналогом винаходу є спосіб ПІД-регулювання, який використовується в більшості систем автоматичного регулювання в техніці та промисловості [1, 2, 3]. 3. Суть винаходу. В основу винаходу поставлено задачу якісного регулювання об'єктами, в тому числі нелінійними, довільного порядку, при наявності затримок та недостатній інформації для побудови точної математичної моделі об'єкту. Для максимального використання «зовнішньої» інформації про характер процесів, що протікають в об'єкті регулювання, пропонується визначення векторної похибки системи автоматичного регулювання (CAP) е, яка відрізняється від загальновживаного визначення похибки, використовуємого в вибраному прототипі ПІД регулювання, а також в (1), і визначається не тільки по різниці величин уставки r і виходу об'єкту регулювання під впливом збурень y але також і фазовим (або в часі) зсувом, виникаючим внаслідок нелінійності, довільного порядку або затримок в об'єкті регулювання. При цьому модуль векторної похибки е, її дійсна еR та уявна еI складові будуть визначатися у відповідності з геометричними співвідношеннями: e r y eR je I. e2 r2 eR r y2 y 2 r y cos ; (2) cos ; eI y sin , де r - модуль вектора уставки, відносно якого визначається зсув вихідного сигналу об'єкту регулювання, y - модуль виміряного вихідного сигналу об'єкта регулювання, - фазовий зсув між сигналом уставки та виміряним вихідним сигналом об'єкту регулювання. Таким чином, дійсна складова векторної похибки eR визначається значенням в момент часу (t) без врахування фазового зсуву, а уявна складова векторної похибки eІ визначається значенням при випередженні (t+ ) або затримці (t) зміни вихідного сигналу об'єкту автоматичного регулювання по відношенню до зміни сигналу уставки. Графічна інтерпретація векторної похибки показана на Фіг.2. Використання запропонованого способу регулювання на основі векторної похибки дозволяє уникнути недоліків традиційного ПІД-регулювання: насичення виходу регулятора під впливом інтегральної складової та перерегулювання під впливом диференційної складової. Даний спосіб дозволяє досягти кращого рішення при проектуванні САР в умовах значної невизначеності математичної моделі об'єкту регулювання. З врахуванням запропонованого способу цільова функція CAP з викорис 4 танням векторної похибки може бути визначена у вигляді: lim G(u, e, ) t 1 T u2 r 2 y ) dt 0 T 0 2 y r cos min, (3) Практично, щоб реалізувати в CAP вимірювання векторної похибки, необхідно виміряти фазовий зсув між сигналом уставки та виміряним вихідним сигналом об'єкта регулювання. З врахуванням запропонованого визначення векторної похибки (2) і по аналогії з законом регулювання для ПІД регулятора, спосіб регулювання на основі векторної похибки може бути записаний у вигляді: u=KR·eR+KІ·eI, (4) де KR - коефіцієнт по дійсній складовій векторної похибки, відповідаючий пропорційній частині традиційного ПІД регулятора, KІ - коефіцієнт по уявній складовій векторної похибки, відповідаючий в залежності від знаку інтегральній або диференційній частині традиційного ПІД регулятора. Значення дійсної еR та уявної еІ складових векторної похибки нелінійно залежать від значення в замкнутому контурі регулювання. Відповідно, значення нелінійних коефіцієнтів KR та KІ для досягнення якісних показників перехідного процесу повинні змінюватися. У відповідності до Фіг.2 запропоновані наступні залежності коефіцієнтів KR та KІ від зсуву : KR=KR0·cos ·sign(eR), (5) KI=KI0·sin ·sign(eI). Структурна схема CAP, побудована на запропонованому способі регулювання на основі векторної похибки (1)-(5), показана на Фіг.3. Для досягнення оптимальних характеристик CAP математичні залежності в (4), (5) вихідного сигналу регулятора від значень складових векторної похибки та зсуву можуть бути замінені іншими математичними операціями. Для доказу того, що запропонований спосіб регулювання на основі векторної похибки може бути використано в CAP різноманітними об'єктами, в тому числі нелінійними, довільного порядку, при наявності затримок та недостатній інформації для побудови точної математичної моделі об'єкту, достатньо привести вираз векторної похибки для випадку =0: e2 (r eR r2 y2 y ) r 2 y 2 r y e cos r cos y r (6) y eI y sin 0 Тобто в цьому випадку значення векторної похибки та її реальної складової відповідають значенню похибки, що використовується для вибраного прототипу - способу ПІД-регулювання, з послідуючим знаходженням інтегральної та диференціальної складових. Таким чином, введення векторної похибки і визначення її уявної складової дозволяє уникнути досить складних математичних операцій інтегрування та диференціювання, та відслідковувати нелінійність, довільний порядок, наявність затримок та досягати якісних характери 5 стик САР при недостатній інформації для побудови точної математичної моделі об'єкту. 4. Перелік фігур, креслень. Фіг.1 - структурна схема САР. На фігурі позначено: r - задане значення вихідного сигналу об'єкта регулювання (уставка); е=r-y - похибка автоматичного регулювання; u - вихідний сигнал регулятора; у - вихід об'єкту; d - збурення (зовнішнє або внутрішнє внаслідок зміни параметрів або структури об'єкту); y - визначений вихідний сигнал об'єкту автоматичного регулювання під впливом збурень. Фіг2 - геометрична інтерпретація векторної похибки. На фігурі позначено: e - векторна похибка; r - модуль вектора уставки, відносно якого визначається зсув вихідного сигналу об'єкту; y - модуль вихідного сигналу об'єкта регулювання; - фазовий зсув між вектором уставки та вектором вихідного сигналу об'єкту регулювання; eR - дійсна складова векторної похибки; eI - уявна складова векторної похибки. Фіг.3 - структурна схема CAP, побудована на запропонованому способі регулювання на основі векторної похибки (1)-(5). На фігурі позначено: r(t) - задане значення вихідного сигналу об'єкта регулювання (уставка); y (t) - визначений вихідний сигнал об'єкту автоматичного регулювання під впливом збурень; e(t) - сигнал векторної похибка; - фазовий зсув між вектором уставки та вектором вихідного сигналу об'єкту регулювання; eR(t) - дійсна складова векторної похибки; eI(t) - уявна складова векторної похибки; КR( ) - коефіцієнт по дійсній складовій векторної похибки; КI( ) - коефіцієнт по уявній складовій векторної похибки. 5.Відомості, які підтверджують можливість здійснення винаходу. Здійснення запропонованого способу регулювання на основі векторної похибки засновано на тому, що в даний час технічна реалізація операції вимірювання частоти та фази сигналів реалізується точніше та простіше ніж реалізація математичних операцій інтегрування, а в особливості диференціювання. Відповідно, пропонований спосіб регулювання на основі векторної похибки має бі 91398 6 льшу точність та завадостійкість, оскільки вимірявши значення фазового зсуву між зміною вектора уставки та вектором виходу об'єкту регулювання τ можливо забезпечити якісне регулювання об'єктами, в тому числі нелінійними, довільного порядку, при наявності затримок та недостатній інформації для побудови точної математичної моделі об'єкту. Для вимірювання фазового зсуву між уставкою r(t) та виміряним вихідним сигналом об'єкта регулювання y (t) можливо використати їх представлення у вигляді аналітичних сигналів за допомогою перетворення Гілберта [4], [5], [6]. Тоді фазовий зсув може бути визначений як: ~ ( t ) r( t ) y ( t ) ~( t ) y r (t) ( t ) arctan y r ~ ( t ) ~( t ) , (7) y ( t ) r( t ) y r де r( t ), ~( t ) - дійсна та уявна складові аналітиr чного сигналу заданого значення вихідного сигналу об'єкта регулювання (уставки), y ( t ), ~ ( t ) y дійсна та уявна складові аналітичного сигналу виміряного вихідного сигналу об'єкта регулювання. 6. Список літератури, в якій описаний прототип. 1. Li. Υ., Ang Κ.Η. and Chong G.С.Υ., Patents, software and hardware for PID control: an overview and analysis of the current art. IEEE CONTROL SYSTEMS MAGAZINE 26(1), 2006, pp.42-54. 2. Li. Y., Ang K.H. and Chong G.С.Υ., PID Control System: Analysis and Design. ІЕЕЕ CONTROL SYSTEMS MAGAZINE, February, 2006, pp.32-41. 3. В. Денисенко. ПИД-регуляторы: вопросы реализации. СТА 1/2008, с.86-99. 4. М. Rosenblum, J. Kurths. Analyzing Synchronization Phenomena from Bivariate Data by Means of the Hilbert Transform, in: Nonlinear Analysis of Physiological Data, Edited by H. Kantz, J. Kurths, and G. Mayer-Kress (Springier, Berlin, 1998), pp.91-99. 5. Агамалов О.Н. Векторний регулятор на основі перетворення Гглбе/>/ш.//Електроінформ. 2008. - №4. - с.12-18. 6. Oleg N. Agamalov, Design of control systems based on vector error. World Scientific and Engineering Academy and Society (WSEAS), WSEAS Transactions on Systems and Control, Volume 4, Issue 9 (September 2009), pages: 476485, ISSN: 1991-8763, www.worldses.org/iournals/control/control-2009.htm 7 Комп’ютерна верстка А. Рябко 91398 8 Підписне Тираж 26 прим. Міністерство освіти і науки України Державний департамент інтелектуальної власності, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601