Спосіб спектрального визначення інформативних складових в процедурах усунення інформаційної невизначеності

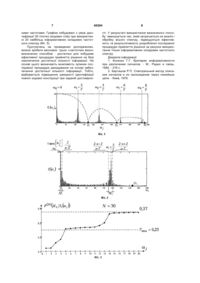
1. Спосіб спектрального визначення інформативних складових сигналу з умов побудови послідовного правила прийняття рішення, який відрізняється тим, що за функцію невизначеності взяте спектральне представлення кодових слів f x   Si j  , яке далі використовують для побудови 3 60394 поділення рk(х) в апостеріорне qk(х). Процес отримання інформації Іk(х), повинен вести до зменшення або повного зняття невинності Ψ(х). Кількість інформації можна визначити, як невизначеність яку можливо зняти при трансформації апріорного розподілення. Тоді, якщо узагальнену міру невизначеності по апріорним ймовірностям ввести таким чином, що Ψ(рk)=φ(f(рk)/рk), а по апостеріорним ймовірностям згідно виразу Ψ(qk)=φ(f(qk)/qk), то в якості міри кількості інформації використовують наступний вираз Ik(x)=1Ψ(qk) [1]. З вище наведеного видно, що задача визначення міри кількості інформації зводиться до знаходження міри невизначеності Ψ(х), котра в свою чергу визначається вибором функції невизначеності f(x). Функція невизначеності бере участь при побудові математичної моделі процедури прийняття рішення. Питання зводиться до визначення умов, які накладаються на неї, а саме: вона повинна монотонно збільшуватись по мірі збільшення кількості задіяних у процедурі можливих станів, а точніше повинна збільшуватись апостеріорна ймовірність правильної ідентифікації з умов послідовного накопичення ітерацій обробки інформативних параметрів сигнальної функції. При розробці статистичної процедури прийняття рішення в задачах відновлення кодової конструкції (кодове слово у вигляді сформованої пачки послідовності радіоімпульсів), необхідно ввести функцію невизначеності f(x), котра задовольняє умовам забезпечення накопичення достатньої міри кількості інформації Ik(x)=1-Ψ(qk) при досягненні заданої ймовірності правильної ідентифікації. Дана задача є багато альтернативною та набуває найбільший інтерес при появі в просторі слабо відмінних кодових слів. Слабо відмінними альтернативними гіпотезами є - гіпотези, що мають слабо відмінні параметри кодових конструкцій, тобто відрізняються на нуль, одну, дві чи три Хемінгові відстані (співпадаючи або на 1-3 біта різниці) [2]. Під кодовими конструкціями будемо розуміти інформаційні сигнали, представлені кодовим словом сформованим на базі методів завадостійкого канального кодування у вигляді послідовності радіо або відео імпульсів. Частіше всього цифрові сигнали представляються, як 32-64 бітові архітектури, а кількість гіпотез при цьому зростає до N→2048. Під інформативними параметрами прийнятого 4 сигналу будемо розуміти спектральне представлення послідовності кодових слів. Даний вид представлення параметрів сигналу є найбільш інформативним для формування порогів прийняття рішення на базі мінімально-достатньої кількості інформації. Для спектрального представлення сигналів використовуємо пряме перетворення Фур'є, тобто даний сигнал буде представлятися у вигляді суми гармонічних коливань з різними частотами. Метою даної моделі є підвищення ефективності та надійності функціонування сучасних інформаційно-комунікаційних систем за рахунок збільшення швидкості ідентифікації та відновлення повної кодової конструкції при заданій достовірності на базі введення нової функції невизначеності. На основі проведених досліджень доводять наступне: використання інформативних частот спектру буде достатньо для побудови послідовної процедури прийняття рішення на основі мінімально достатньої кількості інформації та розрахунку апостеріорної ймовірності правильної ідентифікації. Для досягнення поставленої мети визначають та розроблять функцію невизначеності і розраховують на основі неї узагальнену міру кількості інформації для вирішення задач ідентифікації слабо відмінної бітової архітектури. Вводять, як функцію невизначеності f(x) для вирішення задачі ідентифікації слабо відмінних гіпотез, відповідне спектральне представлення прийнятого інформаційного сигналу Si(ωj). Аналізують та показують, що використання спектрального представлення кодового слова, як функції невизначеності f x   Si j ,   буде найкращим для побудови математичної процедури прийняття рішення з умов збільшення узагальненої міри кількості інформації. Введена функція невизначеності, покликана зменшити інформаційну невизначеність та забезпечити достатню міру кількості інформації. Дана функція надалі буде використовуватися при побудові математичної процедури прийняття рішення, а саме розрахунку міри невизначеності, міри кількості інформації та апостеріорної ймовірності правильної ідентифікації кодової конструкції. Записують функцію невизначеності, як функцію відповідного амплітудно-частотного спектру пачки відео імпульсів (1):   2  T 2   sin  j    l   sin  j    lT  2 lT  2     f x   Si j  Am   S l, j  B l, j , (1)   2  T 2   sin  j       j  lT  2  lT  2   частот (складових) спектру. Для побудови посліде Т - період,  - тривалість імпульсів, ωj - осдовної процедури прийняття рішення, вводять новна частота дискретного спектру пачки (j=1...N поняття ширини «частотних вікон» Δfi в задачах поточний номер спектральних складових), S(l,ωj) ідентифікації слабо відмінних кодових слів. Під функція амплітудно-частотного спектру одиночно«частотним вікном» розуміють - ефективну ширину го імпульсу в пачці, l - кількість імпульсів в пачці, спектру сигналу з умов енергетичного або інфорB(l,ωj) - функція частоти, яка не залежить від формаційного вкладу його гармонійних складових в ми імпульсу та визначається лише їх числом та розрахунок апостеріорної ймовірності правильної періодом слідування [3]. ідентифікації. Після введення нової функції невизначеності, Тоді сумарне значення вікон, які приймають визначають способи знаходження інформативних       5 60394 участь при ідентифікації дорівнює F  n  fi . i 0 Проводять графічний та аналітичний аналіз процедури формування «частотного вікна» та визначають інформативні складові спектру частот для l=32 бітної кодової конструкції з слабо відмінними параметрами (фіг. 1) На основі викладеного визначають, що інформативними частотами є спектральні складові, що формуються біля основних частот дискретного j спектру кодових конструкцій  j  . Дані частоти T j є центрами «частотних вікон»  j  ,j=0, 2 4, …, T n. Ефективну ширину «частотного вікна» запису     умовної  N 1 W Si j / Hk    щільності розподілу Hk / Sl,j Bl, j mij 2 22 k (3) 2k Тоді загальний, Байесовський вираз знаходження апостеріорної ймовірності правильної ідентифікації інформаційного сигналу при умові введення нової функції невизначеності прийме вид:    P Hk / Si  j  e j1 N  j1  1 2k Sl, j Bl, j mij 2 2 2 k e  N N 1  Sl, j Bl, j mij 2 (4) 2 2 i e i1 j 1 2k Запропоновано спосіб визначення інформативних частот спектру на базі введення зазначеної функції невизначеності у розрахунку міри кількості інформації, з урахуванням присутності в кодових послідовностях N «слабо відмінних» кодових слів. На основі проведених досліджень побудовано графік росту ймовірності правильної ідентифікації в залежності від кількості використаних інформативних спектральних складових при багатоальтер N 1 j1 2k  Ik{  k j j   нативних задачах [2] (фіг. 3). Кожна спектральна складова вносить певну міру кількості інформації lk[P(Hk/Si(ωj))], таким чином відповідно збільшує апостеріорну ймовірність правильної ідентифікації P(Hk/Si(ωj)) кодової конструкції. З отриманих результатів можна констатувати, що використання 20 гармонічних складових вносять таку саму міру кількості інформації, як і використання всієї вибірки з 2049 гармонічних складових. Апостеріорна ймовірність правильної ідентифікації при використанні всієї вибірки прий(2049) має значення Р (Hk/Si(ωj))=0,39, а при використанні інформативних складових трьох спектраль(20) них «вікон»: P (Hk/Si(ωj))=0,37. Не велика, але достатня ймовірність порогів правильної ідентифікації відповідає встановленим умовам відновлення слабо відмінних кодових слів. При вирішенні стандартної задачі декодування інформаційного потоку даних, пороги будуть приймати стандартні значення на рівні рішень Котельникова, Шеннона, Кульбака, Байеса та Фішера [1]. На основі отриманих виразів (3-5) будують графічну залежність ймовірності правильної ідентифікації від зростаючої міри кількості інформації при використання 20 гармонічних складових (фіг. 4).     2  T 2     sin  j  l  sin  j      lT  2  lT  2     mij   Am   2  T 2     sin  j       j      lT  2  lT  2       2 2 k e N N 1 i1 j1 2k  2 j 2 jl  2 .    lT T lT lT Надалі розглядають тільки три «частотних вікна», які концентрують основну енергію сигналу. Тоді, ефективна ширина «вікна» де знаходиться основна частота дискретизації Δωі, може графічно бути відображена згідно фіг. 2. Тоді, використовуючи введену функцію невизначеності (1), будуємо узагальнену міру невизначеності, на основі якої розраховують мінімально достатню кількість інформації Ik(x), яка використовується при формуванні статистичного правила прийняття рішення та розраховується для кожної гіпотези {Нк}: ють, як fi  j  PH S  B     1 PHk / Si j   1  f PH k //Sl,l, jBl,l, j (2)    Ik P Hk / Si  j Знаходження прийме вид: 6 2 }>Vmin     2  T 2     sin  j  l  sin  j      lT  2  lT  2     mij   Am   2  T 2     sin  j      j      lT  2  lT  2       2 2 i e Для оцінки якості нововведеного способу, побудовано графіки ймовірності правильної ідентифікації від співвідношення сигнал/шум b=σs/σn. (5) 2 Порівнюють, ймовірності правильної ідентифікації при використанні в процедурі всіх складових спектру та трьох частотних «вікон» з 20 інформатив 7 ними частотами. Графіки побудовані з умов ідентифікації 30 гіпотез (кодових слів) при використанні 20 найбільш інформативних складових частотного спектру (Фіг. 5) Ґрунтуючись на проведених дослідженнях, можна зробити висновок: трьох «частотних вікон» визначених способом - достатньо для побудови ефективної процедури прийняття рішення на базі накопичення достатньої кількості інформації. На основі цього визначають можливість зупинки послідовної процедури декодування на основі забезпечення достатньої кількості інформації. Тобто, відбувається підвищення швидкості ідентифікації повної кодової конструкції при заданій достовірно 60394 8 сті. У результаті використання визначеного способу: зменшується час, який затрачується на аналіз і обробку всього спектру, підвищується ефективність та результативність розробленої послідовної процедури прийняття рішення за рахунок використання тільки інформативних складових частотного спектру. Джерела інформації 1. Косенко Г.Г. Критерии информативности при различении сигналов. - М.: Радио и связь, 1982. - 216 с. 2. Карташов Р.П. Спектральный метод описания сигналов и их прохождение через линейные цепи. - Киев, 1976. 9 Комп’ютерна верстка А. Крулевський 60394 Підписне 10 Тираж 24 прим. Міністерство освіти і науки України Державний департамент інтелектуальної власності, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601