Спосіб формування послідовності рівномірно розподілених випадкових чисел

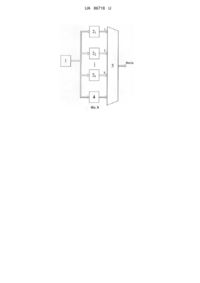
Реферат: UA 86718 U UA 86718 U 5 10 15 20 25 30 35 40 Корисна модель належить до обчислювальної техніки і може бути використана в системах криптографічного захисту, що використовують потокове шифрування. Спосіб формування послідовності рівномірно розподілених випадкових чисел може бути застосований для обміну конфіденційними даними каналами зв'язку будь-якої фізичної природи, що не захищені від несанкціонованого доступу до циркулюючої в них інформації (надалі - відкритими каналами зв'язку), що використовують шифрування простим гамуванням. У зв'язку зі швидким зростанням продуктивності комп'ютерних систем, що використовуються для криптоаналітичних задач, актуальною є задача підвищення криптографічної стійкості систем шифрування. Відомі способи потокового шифрування [1], які передбачають генерацію рівномірно розподіленої послідовності символів (слів) алфавіту у відповідності до певного, прихованого від супротивника, закону, яку називають гамою. Гаму складають посимвольно з відкритим текстом, у результаті чого отримують шифртекст. Цей метод шифрування називають методом простого гамування. Гарантована стійкість шифрування (стійкість, за якої збільшення обсягу перехопленого шифртексту не додає знань про відкритий текст і ключ шифрування) забезпечується за умови виконання наступних умов: рівномірного закону розподілу випадкової послідовності чисел (символів гами шифру) на відрізку [0,(М-1)], де М - потужність використаного алфавіту (цю вимогу можна також трактувати наступним чином: помилка відтворення закону розподілу рівномірно розподіленої випадкової величини, що породжується генератором гами, повинна дорівнювати нулю); відсутність кореляції між символами гами шифру; нескінченно великий період повторення гами. Окрім перерахованого, повинна бути забезпечена стійкість гами шифру до розкриття закону її утворення за відрізком. Цю властивість називають непередбачуваністю гами, а сама гама повинна бути непередбачувана. Жоден з відомих методів генерації гами не задовольняє перерахованим умовам. Цей факт породжує безперервний процес вдосконалення методів генерації криптографічно стійкої випадкової послідовності чисел. Відзначимо, що фізично неможливо реалізувати кінцевий автомат (логічну схему), що породжує послідовність нескінченного періоду. Послідовність, породжувана кінцевим автоматом, має кінцеву довжину, часто велику помилку відтворення закону розподілу символів гами [2] і кореляцію між її символами. Наприклад, для генераторів конгруентних послідовностей чисел наступний символ пов'язаний з попереднім рівнянням (передбачуваність визначена рівнянням): S(n)  KS(n  1)  C M , (1) де К, С,М - параметри генератора, S(n) і S(n  1) - слова, що утворені в поточний - "n" - і в попередній - "n-1" - дискретні моменти часу. Для рекурсивних генераторів на регістрах зсуву (генераторів М-послідовностей) передбачуваність визначена рівнянням: k 1 S(n)   gi S(n  i) , (2) i1 k 1 де g i - коефіцієнти генераторного полінома G( x )   gi x i . i0 45 50 55 Суттєвим є те, що в рівнянні (1) всі операції виконуються в арифметичному полі (вираз "А+В" означає операцію арифметичного додавання чисел А і В), у той час як в (2) всі операції виконуються в полі GF(2) (вираз "А+В" означає операцію додавання многочленів А і В за модулем два), а кінцевим результатом і в тому, і в іншому випадку є випадкова послідовність чисел деякого відрізку. Удосконалення методів формування гами (з метою підвищення криптографічної стійкості шифру) зводиться до спроб усунення зазначених недоліків. У [2, 3] показані способи зменшення помилки відтворення закону розподілу дискретної випадкової величини (шляхом рандомізації послідовності) до нульового значення. У [4] визначені способи усунення кореляційних зв'язків у послідовності шляхом її декореляції. Відомі також способи одержання непередбачуваної рівномірно розподіленої випадкової послідовності чисел за допомогою стохастичних генераторів [5]. Під стохастичним генератором розуміється генератор, який породжує стохастичний випадковий процес - процес, що розвивається в часі згідно із законами теорії 1 UA 86718 U 5 10 15 20 25 30 35 40 45 50 55 60 ймовірності [6], при цьому стан стохастичного процесу в деякий момент часу не може бути визначений за його первісним станом. Найбільш близьким за своєю суттю до запропонованої корисної моделі є спосіб перетворення випадкових чисел з довільним законом розподілу в випадкові числа з рівномірним законом розподілу [7]. Суть корисної моделі полягає в тому, що в послідовності випадкових чисел, що має довільний закон розподілу, здійснюється вибірка декількох найменших значущих розрядів, що дають рівномірно розподілену послідовність випадкових чисел. Для визначення числа найменших значущих розрядів, які потрібно вибрати, визначається значення частоти Найквіста, за межами якої характеристична функція випадкової величини нехтовно мала. На підставі цих даних обчислюється максимальне число найменших значущих розрядів. Недоліком цього способу є те, що характеристична функція випадкової величини обчислюється точно лише при нескінченному обсязі вибірки. Отримання нескінченного обсягу вибірки фізично неможливо реалізувати, тому скінченність об'єму вибірки призводить до неточності обчислення характеристичної функції і, як наслідок, до неточності визначення максимального числа найменших значущих розрядів. Наслідком цих неточностей є те, що закон розподілу дискретної випадкової величини на виході перетворювача відрізняється від рівномірного закону розподілу, що знижує криптографічну стійкість системи. Задачею корисної моделі є створення способу формування послідовності рівномірно розподілених випадкових чисел з наступними властивостями: непередбачуваністю; нульовою помилкою відтворення закону розподілу випадкової величини; скінченного, але дуже великого періоду повторення; зменшеною кореляцією між символами послідовності. Технічним результатом є підвищення криптографічної стійкості послідовності рівномірно розподілених випадкових чисел за рахунок надання їй вказаних властивостей. Суть корисної моделі полягає у використанні декількох різнотипних стохастичних генераторів рівномірно розподілених випадкових чисел з поєднанням результатів їх генерації на виході. Процес формування послідовності містить наступні етапи: рандомізація послідовностей, що генеруються різними за типом і параметрами первинними k генераторами. Тип і параметри генераторів тримаються в секреті. Процедура рандомізації приводить період повторення послідовностей на виході кожного генератора до значення, рівного М. Для цього досить зробити об'єднання (конкатенацію) всіх циклів генератора в один цикл довжиною М; формування послідовності відбувається блоками по М символів; кожен із генераторів, що обчислює наступний символ за рівняннями (1) або (2), перетворюється в генератор стохастичного типу. У такому генераторі за попереднім словом S(n) формується не слово S(n+1), a слово S(n+t), де t - деяке випадкове число відрізка [0,(М-1)], при цьому порядок формування випадкового числа t тримається в секреті. Спосіб формування послідовності рівномірно розподілених випадкових чисел може бути реалізований за допомогою пристрою, показаного на кресленні. Пристрій містить: процесор управління формувачем послідовності 1; група з k різнотипних стохастичних генераторів випадкових чисел (генератори конгруентних чисел і генератори М-послідовності в довільному поєднанні) 21, 22…2k; мультиплексор вибору стохастичного генератора 3, що формує поточний стохастичний цикл (цикл, у якому кожне з М значень випадкової величини відрізка [0,(М-1)] застосовується рівно по одному разу); адаптер сполучення адресних входів мультиплексора із загальною шиною процесора 4. Пристрій працює наступним чином. Керуючий процесор 1 вибирає один з k стохастичних генераторів випадкових чисел 21, 22…2k для формування поточного стохастичного циклу. Одночасно процесор завантажує в вибраний стохастичний генератор змінні дані, які можуть виступати як ключ шифрування: параметри К і С - для генераторів конгруентних чисел; генераторний поліном - для генераторів М-послідовностей; таблицю перестановок порядку формування слів у стохастичному циклі. Після завантаження всіх змінних даних стохастичний генератор формує стохастичний цикл (з М слів), який через мультиплексор 3 виводиться на вихід пристрою. Далі процес повторюється з іншим генератором, призначеним для формування наступного стохастичного циклу, і, відповідно, з іншими змінними даними. 2 UA 86718 U 5 10 15 20 25 30 35 40 Основним блоком формувача послідовності випадкових чисел є стохастичний генератор послідовності рівномірно розподілених випадкових чисел з нульовою помилкою відтворення закону розподілу дискретної випадкової величини. У групі з k генераторів у довільному поєднанні використовуються генератори конгруентних чисел (рівняння (1)) і генератори М-послідовності (рівняння (2)). Для генераторів конгруентних чисел використовуються різні значення параметрів К і С і єдине значення параметра М. Для генераторів М-послідовностей використовуються різні генераторні поліноми одного і того ж степеня n=log2 М. У результаті рандомізації довжина циклу кожного з генераторів стає рівною М (це означає, що в циклі кожне зі слів ряду 0,1,2 … (М-1) застосовується рівно по одному разу). Символи в кожному з цих циклів розподілені рівномірно, а помилка відтворення рівномірного закону розподілу в межах циклу дорівнює нулю. Однак отримана послідовність передбачувана і корельована. Генератори циклічного типу перетворюються в генератори стохастичного типу. Для цього символи циклу нумеруються числами 0,1,2 … (М-1). У результаті утворюється таблиця відповідності чисел натурального ряду символам рандомізованої послідовності. Додатково створюється масив чисел натурального ряду 0,1,2 … (М-1). Над числами цього масиву у відповідності до деякої таблиці проводиться операція перестановки. Для прикладу, замість послідовності 0,1,2,3,4,6,7,8,9,10 у результаті перестановки можна отримати послідовність 7,4,2,6,0,3,10,8,1,5,9. Ця послідовність трактується так: першим обчислюється символ, віддалений на t1=7 символів від деякого початкового значення S (0); другим обчислюється символ, віддалений на t2=4 символи від S (0); третім обчислюється символ, віддалений на t3=2 символи від S (0); четвертим обчислюється символ, віддалений на t4=6 символів від S (0) і т.д. Виконання вказаних операцій призводить до того, що в кожному стохастичному циклі кожне слово відрізку [0,(М-1)] застосовується рівно по одному разу (помилка відтворення рівномірного закону розподілу випадкової величини дорівнює нулю). Внаслідок виконання операції перестановки допоміжного масиву натуральних чисел після кожного стохастичного циклу максимально можливий період повторення блоків генерованої послідовності дорівнює загальному числу перестановок М різних чисел - М!. Таким чином, максимально можливий період повторення послідовності для пропонованого способу дорівнює М! стохастичних циклів . або L = М М! слів. Так, у прийнятого в комп'ютерних системах алфавіту з 256 символів (число розрядів символу алфавіту n=8) максимально можливий період генерованої послідовності буде . . . 509 дорівнювати L=M М! = 256 256! = 2,2 10 символів. 18 Припустимо, що криптоаналітик супротивника перебирає 10 ключів за секунду (зазначимо, що поява комп'ютерів такої продуктивності в осяжному майбутньому малоймовірна). Врахуємо, . 7 що рік - це 3,15 10 секунд. Тоді для того, щоб зламати гаму, знадобиться не більше T 10 18 M  M! 2,2  10 509   7  10 483 років, що фізично неможливо реалізувати.  3,15  10 7 3,15  10 25 Відзначимо також, що за умови виконання операції перестановки допоміжного масиву натуральних чисел, що визначає послідовність обходу k первинних генераторів, після кожних k стохастичних циклів максимально можливий період повторення символів генерованої послідовності досягає значення L=HOK(M k k!; M M!). Якщо k  . . 45 Якщо k - просте і k  . M , то L=HOK(M.k.k!; M.M!)=k.M.M!. 2 . . . . M , то L=HOK(M.k.k!; M.M!)=M.M!. 2 . 509 Для М = 256 і k=15L=НОК(256 15 15!; 256 256!) = 256 256! = 2,2 10 символів. Для М = 256 і . . . . . . 511 k=131L=НОК(256 131 131!; 256 256!) = 131 256 256! = 2,9 10 символів. 50 Джерела інформації: 1. Иванов М.А. Теория, применение и оценка качества генераторов псевдослучайных последовательностей / М.А. Иванов, И.В. Чугунков. -М.: КУДИЦ-ОБРАЗ, 2003.-240 с. 2. Митянкина Т.В. Рандомизация последовательности конгруэнтных чисел / Т.В. Митянкина, В.В. Швыдкий, А.И. Щерба // Вестник Инженерной академии Украины.-2008. - №2. - С. 107-111. 3 UA 86718 U 5 10 15 3. Патент № 41079 Україна, МПК G 06 F 7/58. Спосіб рандомізації послідовності конгруентних чисел / Мітянкіна Т.В., Швидкий В.В., Щерба А.І., Мітянкін М.О.; заявник та патентовласник ЧДТУ. -№u200808187; заявл. 17.06.2008; опубл. 12.05.2009, Бюл. № 17. 4. Патент № 40649 Україна, МПК G 06 F 7/58. Пристрій декореляції випадкової послідовності чисел / Мітянкіна Т.В., Швидкий В.В., Мітянкін М.О.; заявник та патентовласник ЧДТУ. №u200811384; заявл. 22.09.2008; опубл. 27.04.2009, Бюл. № 8. 5. Береза А.С. Генерация конгруэнтных последовательностей чисел с наперед заданными свойствами / А.С. Береза, А.А. Лавданский, В.В. Швыдкий, Э.В. Фауре // Вісник Черкаського державного технологічного університету. - 2012. - №2. - С. 3-8. 6. Бокс Дж., Дженкинс Г. Анализ временных рядов, прогноз и управление / Дж. Бокс, Г. Дженкинс; [пер. с англ. под ред. В.Ф. Писаренко]. - М.: Мир, 1974.-Кн. 1.-406 с. 7. Пат. 2343628 Российская Федерация, МПК Н 03 М 7/00, G 06 F 7/58, G 06 F 17/18. Способ преобразования случайных чисел с произвольным законом распределения в случайные числа с равномерным законом распределения / Амербаев В.М., Зверев Е.М., Романец Ю.В., Шарамок А.В.; заявитель и патентообладатель Общество с ограниченной ответственностью Фирма "Анкад" - № 2007100233/09; заявл. 11.01.2007; опубл. 10.01.2009, Бюл. №1. ФОРМУЛА КОРИСНОЇ МОДЕЛІ 20 25 30 35 n 1. Спосіб формування послідовності рівномірно розподілених на відрізку [0,(2 -1)] випадкових чисел, що використовує групу з k різних генераторів випадкових n-розрядних чисел відрізка n n [0,(2 -1)] з періодами, рівними М=2 , який відрізняється тим, що послідовність рівномірно розподілених випадкових чисел генерується блоками по М чисел, кожен з блоків формується генератором, що визначається за допомогою допоміжної випадкової послідовності k неповторюваних чисел відрізка [1,k], елемент послідовності в блоці, що породжується i-тим генератором, визначається шляхом обчислення символу Si(0+t), віддаленого від деякого визначеного символу Sj(O) на випадкову величину t[0,(М-1)], при цьому значення t для кожного символу в блоці визначається з допоміжної послідовності М неповторюваних чисел відрізка [0,(М-1)], над числами допоміжних послідовностей k неповторюваних чисел відрізку [1,k] і М неповторюваних чисел відрізку [0,(М-1)] виконуються операції перестановки після формування кожних k блоків і М символів (одного блока), відповідно. 2. Спосіб за п. 1, який відрізняється тим, що як генератори випадкових n-розрядних чисел n відрізка [0,(2 -1)] використовуються генератори конгруентних чисел і генератори Мn послідовностей, при цьому рівномірний розподіл чисел на відрізку [0,(2 -1)] в кожному блоці послідовності досягається за рахунок конкатенації всіх циклів генератора конгруентних чисел n або генератора М-послідовності в єдиний надцикл довжиною М=2 або вибором коефіцієнтів К і С генератора конгруентних чисел. Комп’ютерна верстка Г. Паяльніков Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601 4