Спосіб швидкого двовимірного перетворення хаара
Номер патенту: 69490
Опубліковано: 15.09.2004
Автори: Корольова Наталія Анатоліївна, Гіневський Михайло Іванович, Бохан Костянтин Олександрович
Формула / Реферат
Спосіб швидкого двовимірного перетворення Хаара, призначений для виконання швидких двовимірних ортогональних перетворень у базисі Хаара масивів розмірності NxN, що потребує 2N2 операцій множення та 4(N-1)N операцій додавання/віднімання, який відрізняється тим, що для N=8 використовується швидкий двовимірний алгоритм, який заснований на двовимірному базисі Хаара і який складається з трьох ітерацій і процедур трьох типів:
- процедури типу А:
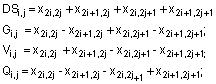
- процедури типу В:
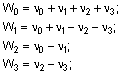
- процедури типу С:
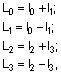
при цьому під час першої ітерації рівнобіжно виконується 16 процедур типу А над блоками 2х2 вихідного блока зображення 8х8 і формується 16 коефіцієнтів перетворення Хаара та матриці DS1, G1, VI розмірністю 4х4, під час другої ітерації паралельно виконується 8 процедур типу В над стовпцями матриці VI та рядками матриці G1 й 4 процедури типу А над блоками 2х2 матриці DS1, формується 36 коефіцієнтів перетворення Хаара та три матриці розмірністю 2х2 (DS2, V2, G2), під час третьої ітерації виконується 3 процедури типу С над матрицями DS2, V2 та G2, в результаті яких формуються останні 12 коефіцієнтів перетворення, а результатом виконання алгоритму є матриця коефіцієнтів перетворення Хаара (трансформанта Хаара), яка складається з 64 елементів.
Текст
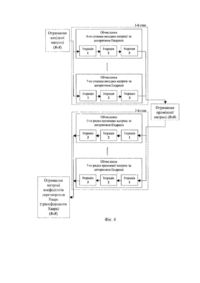
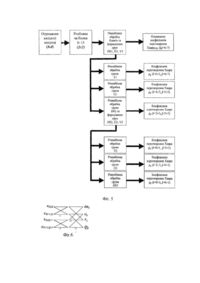
Запропонований винахід відноситься до автоматики й обчислювальної техніки і може бути використаний, зокрема, у системах обробки і відображення інформації. Відомий спосіб швидкого двовимірного ортогонального перетворення Хаара з використанням властивості подільності ортогональних базисів й швидкого алгоритму Кулі-Т'юкі [1] (с. 44-46), [2] (с. 292-298). Властивість подільності полягає в можливості використовува ти для виконання двовимірних перетворень одномірних ортогональних базисів й швидких алгоритмів, та визначається наступним матричним співвідношенням: 1 Y(n) = 2 H(n) X(n)HT (n), N де X(n) - ви хідна матриця N´ N ; H (n ) - матриця Хаара N´ N ; T H (n ) - транспонована матриця Хаара; Y(n ) - матриця коефіцієнтів перетворення Хаара (трансформанта) N´ N . Відомий спосіб складається з двох етапів: - обробка за алгоритмом Кулі-Т'юкі стовпців вихідної матриці розмірністю N´ N (де N=2n, n=1, 2, 3,...), результатом якої є проміжна матриця ( N´ N ); - обробка за алгоритмом Кулі-Т'юкі рядків проміжної матриці, результатом якої є матриця коефіцієнтів Хаара ( N´ N ). На фіг.1 у виді гра фа представлений швидкий алгоритм Кулі-Т'юкі для N=8, на якому: x(i), (i = 0, N - 1) ~ (i ) x (i ) x елемент вихідного вектора, j - елемент вектора після j-ї ітерації, j - елемент вектора після війкової інверсії значення i (дзеркальне відображення двійкового представлення значення і, при якому міняються місцями молодший розряд й відповідний старший розряд (фіг.2.)), точками з'єднання відрізків показані формуємі суми, «-1» під відрізком вказує, що доданок входить у суму з коефіцієнтом -1. Завершальною операцією отримання елемента трансформанти Хаара y x (i) є помноження сформованих сум на коефіцієнт, зазначений над відрізком, праворуч від якого знаходиться відповідний елемент трансформанти. Алгоритм Кулі-Т'юкі при N=8 складається з трьох ітерацій, які визначаються співвідношеннями: 1) перша ітерація: ~( ) = x(l); x N x1(i) = ~(i) + ~( + i); x x 2 N ~(i) - ~( N + i), x1( + i) = x x 2 2 де: - двійкова інверсія значення l; наступними l = 0,7, i = 0,3. 2) друга ітерація: N x 2 (i) = x1(i) + x1( + i); 4 N N x 2 ( + i) = x1(i) - x1( + i); 4 2 ~ ( ) = x (l + N ); x1 1 2 N 2 ~ y x (l + ) = × x1(l ), 2 8 де: l = 0,3, i = 0,1 . 3) третя ітерація: 1 y x (0 ) = × (x 2 ( 0 ) + x2 (1)); 8 1 y x (1) = × ( x 2 (0 ) + x 2 (1)); 8 ~ (0) = x (2); x2 2 ~ (1) = x (3); x 2 y x (2 ) = 2 2 ~ × x 2 (0 ); 8 2 ~ × x2 (1). 8 Для виконання швидкого двовимірного перетворення Хаара матриці розмірності 8´8 відповідно до відомого способу необхідне виконання 2N2 множень, 4(N-1)N - додавань/віднімань й 2NLog2N двійкових y x (3 ) = інверсій. Недоліками відомого способу є: - необхідність виконання великої кількості двійкових інверсій, що збільшує час виконання перетворення; - необхідність виконання перетворення в два етапи й при цьому неможливість початку виконання процедур другого етапу перетворення до закінчення виконання всіх процедур першого етапу, що збільшує час виконання перетворення в цілому; - обмежені можливості по рівнобіжному виконанню процедур перетворення; - необхідність у додатковій пам'яті для збереження проміжної матриці; - нагромадження помилок округлення, що пов'язано за участю помилок, сформованих на першому етапі перетворення, в операціях другого етап у. Найбільш близьким до запропонованого технічним рішенням, обраним як прототип, є спосіб швидкого двовимірного ортогонального перетворення Хаара з використанням властивості подільності ортогональних базисів й швидкого алгоритму Ендрюса [1] (с.148-149), який складається з двох етапів: - обробка за алгоритмом Ендрюса, стовпців вихідної матриці розмірності N´ N (де N=2n, n=1, 2, 3,...), результатом якої є проміжна матриця ( N´ N ); - обробка за алгоритмом Ендрюса рядків проміжної матриці, результатом якої є матриця коефіцієнтів Хаара ( N´ N ). Швидкий алгоритм Ендрюса для N=8 (фіг.3) складається з трьох ітерацій і визначається наступними співвідношеннями: 1) перша ітерація: x1(2i) = x( 2i) + x( 2i + 1); x1(2i + 1) = x(i) - x( 2i + 1); yx ( N 2 + i ) = × x1( 2i + 1), 2 8 де i = 0,3 ; 2) друга ітерація: x 2 (2i) = x1( 2i) + x 1(2i + 1); x 2 (2i + 1) = x1(i) - x1(2i + 1); yx ( N 2 + i) = × x2 (2 i + 1), 4 8 де i = 0,1 ; 3) третя ітерація: 1 y x (0 ) = × (x 2 (0 ) + x 2 (1)), 8 1 y x (1) = × ( x 2 (0 ) - x2 (1)). 8 Для виконання швидкого двовимірного перетворення Хаара матриці розмірності 8´8 у відповідності зі способом, що прийнятий за прототип, необхідно 2N2 операцій множення і 4(N-1)N операцій додавання/віднімання. Недоліками способу-прототипу є: - необхідність виконання перетворення в два етапи й неможливість виконання процедур другого етапу перетворення до закінчення виконання всіх процедур першого етапу, що збільшує час виконання перетворення в цілому; - обмежені можливості по рівнобіжному виконанню процедур перетворення; - необхідність у додатковій пам'яті для збереження проміжної матриці; -нагромадження помилок округлення, що пов'язано з участю помилок, сформованих на першому етапі перетворення, в операціях другого етап у. В основу винаходу поставлена задача створити спосіб швидкого двовимірного перетворення Хаара, який дозволить при одноетапному алгоритмі перетворення виконувати більшість операцій паралельно без значного ускладнення алгоритму й додаткових витрат пам'яті, що істотно зменшить помилки, які виникають при виконанні операцій перетворення, та час виконання перетворення. Поставлена задача вирішується за рахунок використання в способі швидкого двовимірного перетворення Хаара одноетапного швидкого алгоритму перетворення, заснованого на двовимірному базисі Хаара, при цьому вхідна матриця, наприклад 8´8, розбивається на 16 блоків 2´2, над якими виконується перша ітерація алгоритму, у ході якої паралельно обчислюються попарні суми/різниці елементів кожного з отриманих блоків. В результаті першої ітерації формується чотири групи по 16 значень (по чотири значення для кожного блоку, кожне з яких входить до відповідної групи). Одна з груп помножується на коефіцієнт «4», в результаті чого y (i, j = 4,7) отримаємо коефіцієнти перетворення Хаара ij . Інші групи беруть участь в операціях наступної ітерації, в ході якої відбувається їх рівнобіжна обробка (обчислюються попарні суми/різниці елементів груп). В результаті другої ітерації формується чотири групи по 4 значення, помноживши одну з них на коефіцієнт «2», отримаємо коефіцієнти перетворення Хаара значень останніх двох груп на yij (i = 2,3, j = 2,3) коефіцієнт «2 2 » , і дві групи по 8 значень. При помноженні отримаємо коефіцієнти перетворення Хаара yij (i = 2,3, j = 4,7) й yij (i = 4,7 j = 2,3) коефіцієнти перетворення Хаара , а при їх попарній сумі/різниці й помноженні на коефіцієнт «2» отримаємо yij (i = 0,1 j = 4,7) й yij (i = 4,7, j = 0,1) . Інші три групи беруть участь в операціях y (i, j = 0,1) наступної ітерації. Результатом обробки першої групи є коефіцієнти перетворення Хаара ij . Помноженням результатів обробки другої й третьої груп на коефіцієнт « 2 » одержуємо коефіцієнти yij (i = 0,1 j = 2,3 ) yij (i = 2,3 j = 0,1) перетворення Хаара тa . На цьому алгоритм двовимірного швидкого перетворення Хаара для матриці 8´8 завершує свою роботу. Результатом виконання алгоритму являється матриця 8´8 коефіцієнтів перетворення Хаара (трансформанта Хаара). Технічний результат, який може бути отриманий при здійсненні винаходу полягає в створені одноетапного швидкого алгоритму двовимірного перетворення Хаара с рівнобіжним виконанням більшості операцій перетворення, використання якого дозволить істотно зменшити витрати часу на виконання перетворення та величину помилок округлення. На фіг.1 приведений граф алгоритму Кулі-Т’юкі. На фіг.2 приведений приклад двійкової інверсії перших сім чисел. На фіг.3 приведений граф алгоритму Ендрюса. На фіг.4 приведена блок-схема способу швидкого двовимірного перетворення Хаара, який прийнятий за прототип. На фіг.5 приведена блок-схема запропонованого способу швидкого двовимірного перетворення Хаара. На фіг.6 приведений граф процедури типу А. На фіг.7 приведений граф процедури типу В. На фіг.8 приведений граф процедури типу С. Суть способу, що пропонується, полягає у використанні для виконання швидких двовимірних перетворень Хаара одноетапного двовимірного швидкого алгоритму перетворення, який базується на двовимірному базисі Хаара і для матриці розмірності N´ N складається з log2N ітерацій. Для N=8 алгоритм складається з трьох ітерацій, які складаються з процедур трьох типів (А, В, С). Процедура типу А визначається наступними співвідношеннями: DSi, j = x2i,2 j + x 2i +1,2 j + x 2i, 2 j+ 1 + x 2i +1,2 j +1; G i, j = x 2i,2 j - x 2i+ 1, 2 j + x 2i,2 j +1 - x2i +1,2 j +1; Q i, j = x2i,2 j - x 2i+ 1, 2 j - x 2i,2 j +1 + x 2i+ 1, 2 j+ 1; Процедура типу В визначається співвідношеннями: W0 = n 0 + n 1 + n 2 + n 3 ; W1 = n 0 + n 1 - n 2 - n 3 ; W2 = n 0 - n1; W3 = n 2 - n 3 . Процедура типу С визначається співвідношеннями: L0 = l0 + l1; L1 = l0 - l1; L2 = l2 + l3 ; L3 = l2 - l3 . Перша ітерація починається з розбивки вихідної матриці на блоки розмірністю 2´2, над якими виконується процедура А i, j = 0,3 . В результаті виконання першої ітерації одержуємо три групи значень, організованих у y = 4 × Q i, j (i, j = 0,3) виді матриць DS1, G1, V1 розмірністю 4´4 та 16 коефіцієнтів перетворення Хаара 4 +i,4 + j . Друга ітерація алгоритму складається з рівнобіжного виконання наступних процедур: процедури типу В над стовпцями матриці результатом якої є 16 коефіцієнтів перетворення Хаара V1 (n 0 = V10 .i, n 1 = V11,i , n 2 = V12,i , n 3 = V13,i , i = 0,3) yi,4 + j = 2 2 × W i (і=2,3, j = 0,3 ) і yi,4 + j = 2 × Wi , (і=0,1, j = 0,3 ) ; - процедури типу В над рядками матриці G1 (n 0 = V1i,0 , n1 = V1i,1, n 2 = V1i,2 , n 3 = V1i, 3 , i = 0,3) , результатом y = 2 2 × W j i = 0,3 y = 2 × W j i = 0,3 якої є 16 коефіцієнтів перетворення Хаара 4 +i, j ( j=2,3, ) і 4 +i, j ( j=0,1); - процедури типу А над блоками 2´2 матриці DS1, результатом якої є три матриці розмірністю 2´2 (DS2, y = 2 × Qi, j V2, G2) й 4 коефіцієнти перетворення Хаара 2+ i,2 + j (I,j=0,1). Третя ітерація складається з рівнобіжного виконання наступних процедур: V2 (l 0 = V 2 00 , l1 = V2 10, l 2 = V 2 01, l 3 = V 211 ) - процедури С над матрицею . Результатом процедури є коефіцієнти перетворення Хаара y02 = 2 L0 , y12 = 2 L1, y03 = 2 L2 , y13 = 2 L3 ; - процедури С над матрицею G2 коефіцієнти перетворення Хаара y20 = 2 (l0 = G200 , l1 = G 201, l2 = G 210 , l3 = G211 ). Результатом процедури є L0 , y 21 = 2 L1, y30 = 2 L2 , y31 = 2 L3 ; - процедури С над матрицею DS2, при цьому l0 = DS200 , l1 = DS210 , l0 = DS200 , l3 = DS211. Результатом процедури є коефіцієнти перетворення Хаара y00 = 2 L0 , y10 = 2 L1, y01 = 2 L2 , y11 = 2 L3 . В результаті виконання всіх ітерацій алгоритму отримаємо матрицю ' коефіцієнтів двовимірного перетворення Хаара розмірності N´ N (трансформанту Хаара). Для виконання швидкого двовимірного перетворення Хаара матриці розмірності 8´8 необхідно 2N7 операцій множення й 4(N-1)N операцій додавання/віднімання, при цьому за рахунок одностайного алгоритму виконання перетворення й рівнобіжного виконання більшості операцій, час, що необхідний для перетворення, скорочується в два рази (для обчислювальної системи на базі процесора Celeron 600МГц), а величина помилок округлення в 1.8 рази. Джерела інформації 1. Ахмед Η., Рао К.Р. Ортогональные преобразования при обработке цифровых сигналов: Пер. с англ. / Под ред. И.Б. Фоменко. - М.: Связь. 1980.-248с. 2. Залмазон Л.А. Преобразования Фурье, Уолша, Хаара и их применение в управлении, связи и других областях. - М: Наука, 1989. -496с.
ДивитисяДодаткова інформація
Назва патенту англійськоюMethod of fast twofold haar transform
Автори англійськоюBokhan Kostiantyn Oleksandrovych, Koroliova Nataliya Anatoliivna
Назва патенту російськоюСпособ быстрого двухмерного преобразования хаара
Автори російськоюБохан Константин Александрович, Королева Наталья Анатольевна
МПК / Мітки
МПК: G06F 17/14, G06K 9/62
Мітки: швидкого, спосіб, двовимірного, хаара, перетворення
Код посилання
<a href="https://ua.patents.su/8-69490-sposib-shvidkogo-dvovimirnogo-peretvorennya-khaara.html" target="_blank" rel="follow" title="База патентів України">Спосіб швидкого двовимірного перетворення хаара</a>
Попередній патент: Система автоматичного регулювання потужності багатоциліндрового дизеля
Наступний патент: Спосіб обробки точінням нежорстких деталей типу валів
Випадковий патент: Метробус зчленований чотиримостовий