Спосіб зниження опору тертя тіла шляхом формування в’язкопружного покриття

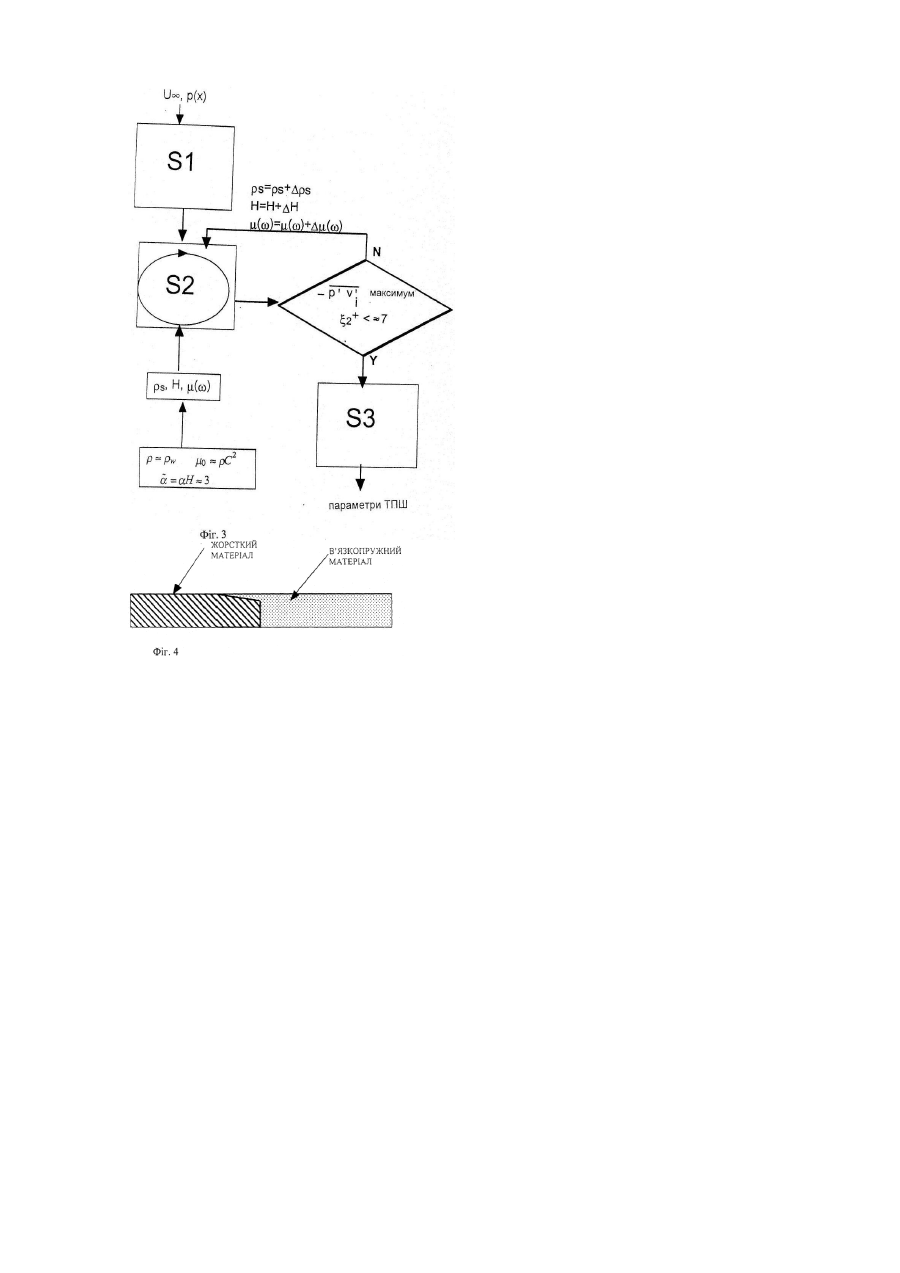
Цей винахід зв'язаний з методологією і розробкою в'язкопружного покриття для зниження опору тертя в турбулентному потоці рідини. В'язкопружне покриття поглинає енергію з турбулентного потоку і модифікує механізм обміну енергії між стінкою і потоком, у результаті чого змінюється локальний профіль швидкості і розвиток пограничного шару. Зі зміною профілю швидкості поблизу стінки також знижується частота турбулентних викидів і зменшується дисипація енергії турбулентності з віддаленням від стінки, що дає зниження опору тертя порядку на 30%. Якщо коливання поверхні в'язкопружного покриття малі, менші ніж товщина в'язкого підшару турбулентного пограничного шару (ТПШ), то збурення, генеровані в рідині коливною поверхнею, будуть залишатися біля стінки, усередині в'язкого підшару. Методологія визначення придатних параметрів для в'язкопружного покриття, що знижує опір, розглядає як розвиток ТПШ при заданих граничних умовах для швидкості й обміну енергії на поверхні, так і деформацію поверхні і поглинання енергії в'язкопружним шаром при заданому поверхневому полі тиску, що моделює ТПШ. З тих пір, як М.О. Kramer заявив про успішні результати експериментів 1957 року, був початий ряд спроб знижувати опір тертя в рідкому турбулентному потоці на поверхні, застосовуючи пасивні податливі покриття. Експериментальні дані в цій області були різнорідними. Більшість дослідників одержали підвищення опору, і тільки деякі заявили про зниження опору в турбулентному потоці. Безліч теоретичних досліджень характеризували стійкість ламінарного пограничного шару на деформівній поверхні, інші характеризували реакцію покриття на пульсаційне навантаження, Однак дотепер не було описано точної аналітичної методики, успішно використаної для дизайну покриття, що знижує опір у турбулентному потоці. У минулому пасивні покриття тестувалися без задання повної системи критичних фізичних параметрів, таких як модуль зсуву, що залежить від частоти, густина і товщина покриття. Для того щоб досягти достовірного зниження опору за допомогою в'язкопружного покриття, потрібна методологія вибору придатних властивостей матеріалу й оцінки очікуваного зниження опору як функції геометрії і швидкості. Відповідна інформація зі зв'язаних технічних питань доступна в літературі і може бути корисною в зв'язку з технічною складністю винаходу. Класичне обговорення теорії пограничного шару, включаючи формулювання рівнянь Нав'є-Стокса і рівнянь турбулентного пограничного шару, дане в Boundary-Layer Theory, Dr. Hermann Schlichting, опубліковане McGraw Hill, New York, seventh edition, 1979. Опис структури і масштабів у турбулентних потоках можна знайти в Turbulence, 1975, McGraw Hill, написаної J.O. Hinze, і в ''Coherent Motions in the Turbulent Boundary Layer," у Annual Review of Fluid Mechanics, 1991, volume 23, pp.601-39, написаної Steven K. Robinson. Обґрунтування моделей турбулентності типу напружень Рейнольдса знаходиться в главі "Turbulent Flows: Model Equations and Solution Methodology," написаної Tom Gatski і включеної до Handbook of Computational Fluid Mechanics, опубліковано Academic Press у 1996. Рівняння в механіці рідини і пружності часто виражені в індексній, чи тензорній формі, для стислості. Розділ 2 у тексті A First Course in Continuum Mechanics, Y.C. Fung, Prentice-Hall, Inc., Englewood Cliffs, NJ, 1977, дає короткий вступ в тензорні позначення і рівняння механіки. Вступ у кінцево-різницеві способи, що використовуються для розв'язування системи рівнянь імпульсів і нерозривності, дано в тексті Computational Fluid Dynamics for Engineers, написаному Klaus Hoffman, і опублікованому the Engineering Education System in Austin, Texas у 1989. Опис виміряних і математично модельованих фізичних властивостей полімерів, даний в Viscoelastic Properties of Polymers, J.D. Ferry, Wiley, New York, 1980, 3rd edition. Стаття "Loss Factor Height and Width Limits for Polymer Relaxation," Bruce Hartmann, Gilbert Lee, and John Lee, у the Journal of the Acoustical Society of America, Vol.95, No. 1, January 1994, обговорює математичний опис модулів зсуву для реальних в'язкопружних полімерних матеріалів, включаючи модельовані відповідно до підходу Havriliak-Negami. Недавно в міжнародній літературі (K.S. Choi, X. Yang, B.R, Clayton, EJ, Glover, M. Atlar, B.N, Semonev, and V.M. Kulik, "Turbulent Drag Reduction Using Compliant Surfaces," Proceedings of the Royal Society of London, A (1997) 453, pp.2229-2240) Чой і колеги повідомили про експериментальні виміри зниження турбулентного опору тертя до 7% на осесиметричному тілі, покритому в'язкопружним матеріалом. Ці експерименти були виконані у Великобританії і використовували покриття, розроблені і виготовлені в Інституті теплофізики Російської Академії Наук, Новосибірськ, групою, очолюваною Б.Н.Семеновим. Базисний підхід до розробки є напівемпіричним і не враховує характеризацію комплексного модуля зсуву в'язкопружного матеріалу, а саме, час релаксації матеріалу, Цей підхід не враховує залежності властивостей матеріалу від частоти. Більш того, концепція новосибірців справедлива тільки для мембранних покриттів, таких як плівка, що складається з піногуми, просоченої водою чи гліцерином, де розглядаються тільки нормальні до поверхні коливання. Структура покриття, призначеного для зниження опору, розглядалася в міжнародній літературі, починаючи з патенту 1938-го року No. 669-897, "An Apparatus for the Reduction of Friction Drag," виданого в Німеччині Max 0. Kramer. Пізніше Kramer одержав патенти в 1964-м, nо. 3,161,385, і 1971-м, nо. 3,585,953, для покриттів, що подовжують ламінарний пограничний шар. Радянські авторські свідоцтва, такі як "A Damping Covering," USSR patent 1413286, Publication 20.01.1974, Bulletin of the Inventions 14, V.V. Babenko, L.F. Kozlov, and S.V. Pershin, "An Adjustable Damping Covering," USSR patent 1597866, Publication 15.03.1978, Bulletin of the Inventions 110, V.V. Babenlco, L.F. Kozlov, and V.I. Korobov, і "A Damping Covering for Solid Bodies," USSR patent 1802672, Publication 07.02.1981, Bulletin of the Inventions 15, V.V. Babenlco and N.F. Yurchenko, також описували структуру покриттів, що знижують опір і містять в'язкопружні матеріали. Ці авторські свідоцтва ідентифікують тривимірну структуру в покриттях, що знижують опір, але не розглядають методологію для визначення придатних параметрів в'язко пружного матеріалу, котру можна було б використовувати при виготовленні таких покриттів. Структурні властивості включають багатошаровість матеріалів, поздовжні включення типу ребер із пружних, в'язкопружних чи рідких матеріалів, елементи, що підігріваються. В'язкопружні покриття можуть бути скомбіновані з іншими формами структури, такими як поздовжні ріблети, сформовані на поверхні чи усередині покриття. Як описується в міжнародній літературі в таких публікаціях, як "Secondary Flow Induced by Riblets," написаній D.B. Goldstein і T.C. Tuan, і опублікованій в Journal of Fluid Mechanics, volume 363, 25 May 1998, pp.115-152, двомірні тверді ріблети самі по собі показали в експерименті зниження опору тертя до 10%. Цей винахід дозволяє конструювати в'язкопружні покриття для зниження турбулентного опору тертя. Покриття з властивостями матеріалу, розробленого за методологією, описаною в цьому винаході знижували опір тертя більш ніж на 10%. Методологія цього винаходу дозволяє, як перший об'єкт винаходу, визначати комплексний модуль зсуву, залежний від частоти, густину і товщину ізотропного в'язкопружного матеріалу, що буде знижувати турбулентний опір тертя щодо конкретних умов потоку на твердій поверхні. Можна оцінити кількісно рівень зниження опору, Дано математичні деталі для випадків турбулентного потоку на твердій гладкій пластині, а також на гладкій в'язкопружній пластині, де винахід враховує і нормальне, і поздовжнє коливання поверхні. Другий об'єкт винаходу - це специфікація матеріальних властивостей покриття, складеного з декількох шарів ізотропних в'язкопружних матеріалів. Третій об'єкт винаходу - це специфікація матеріальних властивостей покриття, складеного з анізотропних матеріалів. Четвертий об'єкт винаходу - це мінімізація ефектів кромки для покриттів кінцевої довжини. П'ятий об'єкт винаходу - це стабілізація поздовжніх вихрів за допомогою комбінації в'язкопружного покриття з додатковими структурами, такими, як ріблети. Методологія, використовувана тут для опису взаємодії турбулентного пограничного шару (ТПШ) з в'язкопружним (ВП) шаром включає дві задачі: 1) задачу гідромеханіки, що включає обчислення параметрів турбулентного пограничного шару при заданих граничних умовах для твердої, пружної чи в'язкопружної поверхні (згадувану тут як ТПШ задача), і 2) задачу теорії пружності, що включає обчислення реакції в'язкопружної чи пружної поверхні на періодичну функцію, що апроксимує навантаження турбулентного пограничного шару. Винахід фокусується на обчисленні амплітуд і швидкостей коливання поверхні і потоку енергії для в'язкопружного покриття (тут згадується як ВП задача). Ці дві задачі зв'язані одна з одною коефіцієнтами, що відносяться до граничних умов на поверхні для поглинання енергії й амплітуд коливання поверхні (далі називані динамічними і кінематичними граничними умовами, відповідно). ТПШ задача розв'язується спочатку для твердої поверхні, даючи необхідні вихідні дані для опису функції на поверхні, а також вихідні значення опору тертя для порівняння. Далі розв'язується ВП задача, при даній періодичній функції, що апроксимує пульсації зсуву і тиску в даному пограничному шарі. Початковий вибір параметрів матеріалу спирається на теоретичні та емпіричні міркування. Оптимальні параметри матеріалу вибираються у результаті послідовних наближень, так, щоб задовольнити наступні критерії: 1) потік енергії у в'язкопружне покриття максимальний і 2) амплітуди коливань поверхні менші, ніж товщина в'язкого підшару турбулентного пограничного шару на покритті. Якщо амплітуди коливання перевищують товщину в'язкого підшару турбулентного потоку, то коливання істотно підсилюють шорсткість поверхні, приводячи до збільшення опору тертя, Більш того, оскільки фазова швидкість збурень у пограничному шарі перевищує швидкість зсувної хвилі в матеріалі, виникає резонансна взаємодія з великими амплітудами хвилі. Таких умов потрібно уникати. Однак помірний потік енергії в матеріал, коли енергія трансформується у внутрішні зсувні хвилі і в остаточному підсумку розсіюється як тепло, приводить до якісних і кількісних змін у балансі енергії, з відповідним зниженням опору тертя. Оптимальні фізичні властивості в'язкопружного матеріалу будуть змінюватися зі швидкістю потоку, що набігає, позицією уздовж тіла, градієнтом тиску, і будь-якими іншими факторами, що впливають на розвиток пограничного шару і характеристики локальних турбулентних пульсацій. Розв'язуючи ТПШ рівняння, можна кількісно оцінити турбулентний опір тертя на в'язкопружній, пружній чи твердій поверхні. У випадку в'язкопружної поверхні, де енергія поглинається і поверхневі коливання ненульові, задаються і динамічні, і кінематичні граничні умови. Ці граничні умови виводяться прямо з розв'язку ВП рівнянь для потоку енергії й амплітуд коливання поверхні, і потім переносяться в граничні умови для дисипации і напружень Рейнольдса для розв'язку ТПШ рівнянь. Вертикальні коливання впливають на ефективну шорсткість поверхні, і середньоквадратичне значення вертикального коливання класифікується як динамічна шорсткість. Якщо амплітуди коливання менші, ніж товщина в'язкого підшару, то можна оцінювати напруження Рейнольдса як нульові. Рівняння турбулентного пограничного шару описують турбулентну дифузію як градієнтне наближення, що вміщує динамічну граничну умову, і вводяться пристінні функції для опису перерозподілу енергії турбулентності в пристінній області для різних поверхонь. Цей винахід стане більш зрозумілим з детального опису, даного нижче, і супровідних фігур креслень, що дані винятково з метою ілюстрації і не є обмежуючими для даного винаходу, де: Фігура 1 - це схема взаємодії пасивного в'язкопружного покриття з турбулентним пограничним шаром, де низкоамплітудна біжуча хвиля розвивається на поверхні, Фігура 1 - це збільшення району усередині кола, показаного на фігурі 1, і показує амплітуди зсуву, і Фігура 3 - це блок-схема базисної методології, потрібної для а) вибору в'язкопружного матеріалу, що знижує турбулентний опір тертя за даних умов потоку, і б) кількісної оцінки зниження опору відносно твердої поверхні, і Фігура 4 показує деталь структури, введеної між в'язкопружним покриттям і твердою поверхнею для зменшення локальної амплітуди коливання й ефектів кромки. Цей винахід визначає фізичні і геометричні параметри в'язкопружного покриття, що знижує опір тертя за даних умов потоку. Більш того, винахід дозволяє оцінити очікувану ефективність зниження опору даного матеріалу з відомими фізичними властивостями для тіла даної конфігурації і визначених умов потоку. Методологія застосовувалася головним чином для характеризації покриттів для турбулентного потоку на плоских пластинах і осесиметричних тілах, і може бути також застосована до більш складних геометрій із кривизною і градієнтами тиску. Рідкий пограничний шар - це дуже тонкий шар рідини, що прилягає до поверхні, над якою тече рідина. Це область, де сили тертя відіграють головну роль, і де потік перебудовується від умов на поверхні до умов у вільному потоці. Зовнішній край пограничного шару традиційно визначається як місце, де відношення β середньої швидкості U до швидкості вільного потоку U є константою, приблизно рівною 1: U U¥ y =1 d =b»1 (Рівняння 1) Значення обраної константи β буде залежати від конфігурації і міркувань чисельної стійкості. Для випадку плоскої пластини значення цієї константи приймається рівним 0:9975. Турбулентний пограничний шар характеризується спектром пульсацій тиску і напружень зсуву. їхня частота, фазова швидкість і амплітудні характеристики є функціями таких факторів, як швидкість вільного потоку, конфігурація тіла, умов на поверхні і градієнт тиску. У випадку потоку на твердій поверхні, руху на поверхні немає. Для пружної чи в'язкопружної поверхні пульсації тиску і зсуву на стінці діють як збурююча функція, що деформує поверхню, створюючи поверхневі хвилі. Для в'язкопружної поверхні енергія з турбулентного пограничного шару може бути поглинена і дисипирована покриттям, що вимагає правильного задания граничних умов на стінці і для напруження Рейнольдса, і.для поглинання енергії (тобто кінематичних і динамічних граничних умов). Фігура 1 - це схема пасивного в'язкопружного покриття, що взаємодіє з турбулентним пограничним шаром товщиною d. Для простоти розглядається випадок потоку зі швидкістю U на покритій пластині, де координати х, у, і z відповідають поздовжньому, нормальному і трансверсальному напрямкам. В іншому випадку χ представлений як x1, у як х2, і z як х3. Передбачається, що рідина є в'язка і нестислива, і що: матеріал покриття в'язкопружний (тобто має комбінацію пружних і в'язких фізичних властивостей). Якщо поверхня тверда, не буде коливань і поглинання енергії, Якщо поверхня пружна чи в'язкопружна, будуть виникати коливання поверхні і, якщо вона в'язкопружна. буде також відбуватись обмін енергією. Компоненти поздовжнього і вертикального зсуву поверхні в'язкопружного матеріалу задані як x 1 і x 2, і динамічна швидкість визначається як: tw (Рівняння 2) r де tw - це напруження зсуву на стінці і r - густина рідини. Взаємодія турбулентного пограничного шару з в'язкопружним покриттям приводить до утворення квазиперіодичної поверхневої хвилі. Рух покриття і поглинання ним енергії (кінематичні і динамічні граничні умови), у свою чергу, впливають на баланс енергії в турбулентному пограничному шарі і величину опору тертя, останнє з який є поверхневим інтегралом напруження зсуву на стінці. Методологію цього винаходу схематично показано на Фігурі 3. Цей винахід включає розв'язок для: 1) параметрів турбулентного пограничного шару (ТПШ), включаючи опір тертя на твердій, пружній чи в'язкопружній пластинах; і 2) поглинання енергії й амплітуд коливання в'язкопружної (ВП) пластини, викликаних періодичним навантаженням, що апроксимує навантаження турбулентного пограничного шару. Ці дві частини розв'язку зв'язані одна з одною граничними умовами, як для енергії, поглиненої поверхнею, так і для амплітуд руху поверхні, і є частиною загальної методології вибору покриттів, що знижують опір, і кількісного визначення зниження опору за даних умов потоку. Нижче описуються ці дві частини розв'язку, а також методологія, що зв'язує їх. Визначення параметрів турбулентного пограничного шару на твердій, пружній чи в'язкопружній поверхнях (ТПШ задача) На фігурі 3 параметри ТПШ спочатку характеризуються для твердої поверхні (крок 1 (S1)) і, після визначення властивостей матеріалу, для в'язкопружного матеріалу (крок 3 (S3)). На кроці 3 застосовується той же базисний підхід, що і на кроці 1, за винятком того, що динамічні і кінематичні граничні умови визначаються по-іншому. На твердій поверхні немає руху і поглинання енергії. На пружній поверхні є рух, але немає поглинання енергії. На в'язкопружній поверхні є рух поверхні і поглинання енергії. Загальна система рівнянь нерозривності, руху й енергії: Параметри турбулентного пограничного шару визначаються за допомогою розв'язку системи рівнянь нерозривності, руху й енергії з відповідними граничними умовами. Ці рівняння виводяться з законів збереження маси, збереження кількості руху (другий закон Ньютона) і балансу енергії (що. спирається на перший закон термодинаміки). У декартових координатах загальне рівняння нерозривності для стисливої рідини з густиною r і компонентами швидкості U, V, і W у поздовжньому, нормальному і трансверсальному напрямках записано нижче в Рівнянні 3: ¶r ¶ (rU) ¶ (rV ) ¶(rW ) + + + =0 (Рівняння 3) ¶t ¶x ¶y ¶z Інакше Рівняння 3 може бути записане в індексній формі (як у Рівнянні 4), де х, у, і z представлені як х1 х2, і x3 відповідно, і U, V, і W представлені як U1, U2, і U3, відповідно. Це значить, що індекс і може мати значення 1, 2 чи 3, і що повторюваний індекс і позначає підсумовування. ¶r ¶ (rUi ) + =0 (Рівняння 4) ¶t ¶xi Рівняння 3 спрощується для нестисливої рідини, тобто, якщо густина рідини постійна, застосовується наступне: ¶r ¶ (rU) ¶ (rV ) ¶(rW ) + + + = 0 (Рівняння 5) ¶t ¶x ¶y ¶z Узагальнені рівняння руху, називані рівняннями Нав'є-Стокса, у випадку нестисливої рідини з постійною в'язкістю виражаються в декартових координатах як: u* = ¶Ui ¶U 1 ¶P ¶ 2Ui + Uj i = + gi + n ¶t ¶x j r ¶x i ¶x j¶x j (Рівняння 6а-6b-6с) У Рівнянні 6: Ρ - це середній тиск, gi - це вектор об'ємної сили внаслідок зовнішніх полів, таких як гравітація, що діють на елемент, і n - це кінематична в'язкість (вважається константою). Потрібно відзначити, що записаний вище вираз в індексній формі представляє три рівняння для трьох компонентів швидкості в напрямках х, у, і z. Компоненти турбулентної швидкості можуть бути описані як сума середньої і пульсаційної компоненти Ui і u', відповідно, де U1, U2 , і U3, еквівалентні U, V, i W, a u'1, u'2, і u'3 еквівалентні u’, n', і w': (Рівняння 7a-7b-7c) Ui = Ui + u'i Риска зверху позначає підсумовування в часі: (Рівняння 8а-8b-8с) Ui = Ui Підставляючи Рівняння 7а-7с у Рівняння 6а-6с і осереднюючи в часі, одержимо наступну систему трьох комплексних нелінійних рівнянь руху турбулентного потоку в частинних похідних другого порядку: Uj ¶u'iu'j ¶Ui ¶2Ui 1 ¶P =+ gi + n ¶x j r ¶ xi ¶x j¶x j ¶x j (Рівняння 9a-9b-9c) 2 2 2 У Рівняннях 9а-9с компонента u' , n' і w ' називаються нормальними напруженнями Рейнольдса, і компоненти у формі - u' n' , - n' w' , і - u' w ' називаються зсувними напруженнями Рейнольдса. Кінетична енергія турбулентності k визначаться як: 1æ ö k = ç u'2 + n'2 + w '2 ÷ (Рівняння 10) 2è ø Замикання узагальненої системи рівнянь, включаючи рівняння нерозривності (Рівняння 5) і рівняння руху (Рівняння 9а-9с), для турбулентного потоку вимагає сімох додаткових рівнянь для характеризації шести u 'u ' напружень Рейнольдса i j швидкості зміни турбулентної енергії k. Цей винахід визначає ізотропну швидкість дисипації, e, що зв'язана з переносом енергії в рідині і через границю рідина-поверхня. Рівняння переносу енергії спираються на перший закон термодинаміки, відповідно до якого зміна тепла dQ в об'ємі за час dt служить для зміни внутрішньої енергії dE і виконання роботи dWK. dQ dE dWK = + (Рівняння 11) {dt {dt dt heat energy work У літературі існує безліч підходів до виводу додаткових рівнянь для компонентів напружень Рейнольдса, але цей винахід використовує методологію типу переносу напружень Рейнольдса, У цій методології напружень Рейнольдса рівняння приймають наступну загальну форму; ¶u'iu'j ¶Jijk (Рівняння 12a-12f) - 2eij ¶xk ¶xk де Pij позначає породження, Пij позначає тензор кореляцій тиск-напруження, Jijk - дифузійний потік напружень Рейнольдса, і e ij - тензор дисипації. У загальному випадку повинні розглядатися рівняння для всіх шести компонентів тензора напружень Рейнольдса і для швидкості дисипації. Рівняння для ізотропної швидкості дисипації e схоже за структурою на рівняннями переносу напружень Рейнольдса. Повні математичні вирази для напружень Рейнольдса й ізотропної швидкості дисипації будуть записані в наступному розділі для окремого випадку двомірного пограничного шару. Коротенько, рівняння, що розв'язуються для визначення параметрів турбулентного пограничного шару, включають: рівняння нерозривності, Рівняння 5, три рівняння руху, Рівняння 9а,9b,9с, шість рівнянь для зсувних і нормальних напружень Рейнольдса, Рівняння 12a-12f, і рівняння для ізотропної швидкості дисипації e (Рівняння 16 нижче). Методологія для знаходження параметрів турбулентного пограничного шару включає кінцево-різницеву апроксимацію системи рівнянь руху і нерозривності з відповідними граничними умовами. Рівняння турбулентного пограничного шару: Повне математичне формулювання дане для часткового випадку нестисливого турбулентного пограничного шару в стаціонарному двомірному осередненому потоці зі швидкістю U. Рівняння двомірного турбулентного пограничного шару виводяться з загального рівняння нерозривності (Рівняння 5) і рівнянь руху (Рівняння 9а-9с), з припущеннями, що: Середня трансверсальна швидкість, W, дорівнює нулю. Гравітацією можна знехтувати. Градієнт тиску в напрямку (у) приблизно дорівнює нулю. Середня швидкість у поздовжньому напрямку, U, набагато більша, ніж середня швидкість у нормальному напрямку, V. Швидкість зміни параметрів у напрямку (х) набагато менша, ніж швидкість зміни параметрів у напрямку (у). Перераховані вище припущення дозволяють спростити набір рівнянь, потрібних для знаходження Uk = Pij - Пij параметрів турбулентного пограничного шару, що буде включати модифіковане рівняння нерозривності (Рівняння 13): ¶U ¶V + =0 (Рівняння 13) ¶x ¶y і рівняння руху для компоненти швидкості U (Рівняння 14): U ¶U ¶U ¶ 2U ¶u' n' 1 ¶P +V =+n 2 ¶x ¶y r ¶x ¶y ¶y (Рівняння 14) У загальному випадку, коли потрібні рівняння переносу для шести компонентів тензора напружень Рейнольдса, зсувні напруження Рейнольдса -n’w’ і -u’w’ вважаються малими, так що тільки рівняння для u’2, n'2, w'2 і -u'w' формулюються у форматі рівняння 12 (повторюваного нижче як Рівняння 15а-15d): ¶u'iu'j ¶Jijk (Рівняння 15а-15d) - 2eij ¶xk ¶xk де Pij - член породження, Пij - тензор кореляцій тиск-напруження, Jijk - дифузійний потік напружень Рейнольдса, і e - тензор дисипації. П'яте рівняння для e таке: ¶e ¶e e eé ¶ 2k ù ¶ æ ¶e ö ¶2 e (Рівнянç 2e t ÷+n +V = Ce1f1 PS - Ce2 f 2 êe - n 2 ú + U ¶x ¶y ¶y ÷ k kê ¶y ú ¶y ç ¶y 2 è ø ня 16) ë û де вираз для в'язкої дифузії може також моделюватися як: æ ¶k1 / 2 ö ¶2k ÷ n » 2 nç (Рівняння 17) ç ¶y ÷ ¶y 2 è ø якщо це потрібно для чисельної стійкості розв'язку для в'язкопружних неколивних поверхонь у пристінній області. У Рівняннях (15a-15d) член Рij можна виразити як: ¶U j ' ¶Ui - u'juk (Рівняння 18а-18d) Pij = -u'iu'k ¶xk ¶xk У Рівнянні (16), член ΡS можна виразити як: 1 PS = Pii (Рівняння 19) 2 Тензор кореляцій тиск-напруження, Пij, що перерозподіляє енергію між різними компонентами напружень Рейнольдса, можна виразити як: (Рівнян2 ö 2 ö æ e öæ æ Пij = C1ç ÷ ç ui'u'j - dij k ÷ + C 2 ç Pij - dij PS ÷ + p'ij,1 +p'ij,2 + p'ij ,3 ня 3 ø 3 ø è k øè è 20a20d) де член p’ij,1 представляє пристінний перерозподіл турбулентної енергії від поздовжнього компонента до нормального і трансверсального, член p’ij,2 представляє пристінну зміну компонентів тензора породження напружень Рейнольдса, і член p’ij,3 представляє пристінний перерозподіл турбулентної енергії пропорційно локальній завихреності: (Рівнян3 eæ ö æ 1ö p'ij,1 = -C1' ç n'2dij - n' u'idj1 + n' u' jdi1 ÷f ç ÷ ня 21açy÷ kè 2 ø è ø 21d) 2 æ ö æ 1ö (Рівняння p'ij,2 = -C2 ' ç Pij - dijPS ÷f ç ÷ ç ÷ 22a-22d) 3 è ø è yø Uk = Pij - Пij ( ( ) æ 1ö p'ij,3 = C3 ' Pij - Dij f ç ÷ ç y÷ è ø ) (Рівняння 23a-23d) æ 1ö fç ÷ ç y÷ Тут è ø - це однозначна демпфуюча функція у пристінній області: æ 1ö R æ 100 ö ÷ f ç ÷ = t ç1 + 1 + (Рівняння 24) çy÷ R ç Rt ÷ è ø k è ø де: Rk = k1 / 2 y n (Рівняння 25) i k2 ne Тут Dij - тензор дифузії: ¶Ul ¶ Ul - u jul Dij = - uiul ¶x j ¶xi Rt = (Рівняння 26) (Рівняння 27a-27d) ¶Jijk ¶x k - градієнт турбулентного і в'язкого потоку напружень Рейнольдса в пограничному шарі, де тільки один з компонентів залишається в наближенні пограничного шару: ¶Jijk = ¶x 2 2 ' ' æ é ùö ç AC k ên '2 ¶u'i u' j ú ÷ + n ¶ uiu j t ç ÷ eê ¶y ú ÷ ç ¶y 2 ë ûø è viscous diffusion ¶ ¶y (Рівняння 28a-28d) turbulent diffusion 2 2 2 де А дорівнює 6 у рівняннях для n' , 2 - для u' й w ' , і 4 для - u' n' (тобто ефективні градієнти дифузії різні для різних компонентів напружень Рейнольдса), і де коефіцієнт турбулентної дифузії, et, дорівнює: k e t = C t n' 2 (Рівняння 29) e за винятком Рівняння (16), де: (Рівняння 30) Ct=Ce Тензор дисипації, e ij, записується як: eij = n ' u'i u' j 1 ¶u'i ¶u j » fs e + (1 - fs ) dije 2k 3 ¶xk ¶xk (Рівняння 31а-31d) де fs характеризує потік у пристінній області: 1 fs = (Рівняння 32) 1 + 0.06R t і; k2 (Рівняння 33) ne Рівняння (16) включає f 1 і f 2 які також вносять поправки в пристінний потік: Rt = f1 = 1 + 0.8e -Rt (Рівняння 34) (Рівняння 35) f2 = 1- 0. 2e -R Значення констант для потоку на плоскій пластині приведені в Таблиці 1: 2 t Таблиця 1 C1 C2 Ce1 Ce2 Ct C’3 Ce C’1 C’2 1.34 0.8 1.45 1.9 0.12 0.15 0.36 0.45 0.036 Для випадку двовимірного пограничного шару параметри турбулентного пограничного шару при різних координатах χ і у визначаються з розв'язку рівняння нерозривності (Рівняння 13), рівнянь руху в напрямку χ 2 2 2 (Рівняння 14), рівняння переносу для напружень Рейнольдса u' , n' , w ' і - u' n' (Рівняння 15a-15d), і рівняння швидкості ізотропної дисипації енергії (Рівняння 16), при заданих граничних умовах, Задача розв'язується чисельно з використанням кінцево-різницевої апроксимації. Усі рівняння приводяться до стандартного виду параболічного рівняння з заданою функцією, і розв’язок знаходять у точках розрахункової сітки в системі координат (х, у). Граничні умови: граничні умови - це значення параметрів на границях пограничного шару, тобто на поверхні й у вільному потоці. Швидкість вільного потоку дорівнює U. Граничні умови на поверхні задаються для нормальних і зсувних напружень Рейнольдса (кінематичні граничні умови), а також для ізотропної швидкості дисипації (динамічні граничні умови). Для довільної геометрії повинні бути задані координати поверхні x і у. Якщо поверхня плоска, граничні умови задаються на лінії у=0. Оскільки амплітуди коливання на поверхні малі, можна застосовувати лінеаризовані кінематичні граничні умови, при яких середні швидкості на поверхні вважаються нульовими. Граничні умови для пульсаційних компонент швидкості на поверхні плоскої пластини виражаються як: u2 ¶x1 (Рівняння 36) cos Q - x 2 * ¶t n ¶x n' y = 0 = 2 (Рівняння 37) ¶t ¶x w ' y = 0 = 1 sin Q (Рівняння 38) ¶t де x 1 і x 2 - це поздовжній і вертикальний зсуви поверхні відповідно, u* - динамічна швидкість (визначена вище), і Q - кут нахилу середнього потоку до поздовжньої осі в. площині x1-х3. При лінеаризованих граничних умовах середні швидкості на поверхні вважаються нульовими. Зсуви поверхні апроксимуються першими модами ряду Фур'є: u' y =0 = xi = ¥ i a j (x -Ct ) å aije j =1 » ai1eia e (x -Ct ) (Рівняння 39) Тут a е - це хвильове число, що відповідає максимуму енергії в пограничному шарі, воно дорівнює: we (Рівняння 40) C де енергонесуча частота w е є така: U we = ¥ (Рівняння 41) d і фазова швидкість, що відповідає енергонесучим збуренням у пограничному шарі, вважається такою: (Рівняння 42) C»0.8U¥ Оскільки існує діапазон частот, на яких існує перенос енергії, як відображено в науковій літературі, корисно також виконати обчислення для випадку, коли: U we = 2 ¥ (Рівняння 43) d У відсутність резонансу доцільно осереднювати в часі компоненти напружень Рейнольдса на стінці: ae = u' 2 = y =0 2 æ 1 2 ç 2 2u2 1 æ u2 ö * we ç x 1 + x1 x2 s in(j2 - j1 ) + 2 ç * ÷ x2 2 we n we ç n ÷ ç ø è è n' 2 = y= 0 w '2 = y =0 u' n ' y =0 1 2 2 we x 2 2 1 2 2 we x1 tan 2 Q 2 = 1 2 we x 2 x1 cos(j 2 - j1 ) 2 ö 2÷ ÷ ÷ ø (Рівняння 44) (Рівняння 45) (Рівняння 46) (Рівняння 47) x де i - це середньоквадратична амплітуда зсуву. Для пасивного ізотропного в'язкопружного покриття, збуджуваного вимушеним навантаженням, реакція набуває форму біжучої хвилі, так що зсув фаз між нормальним і поздовжнім зсувом, j2-j1, буде приблизно π/2, і зсувне напруження Рейнольдса на поверхні буде приблизно нульовим. Для анізотропних матеріалів зсув фаз може бути іншим, так що на стінці можуть генеруватися негативні зсувні напруження Рейнольдса. Для твердої стінки руху на стінці не буде, так що нормальні і зсувні напруження Рейнольдса будуть дорівнюють нулю. Гранична умова для ізотропної швидкості дисипації така: e y =0 = ¶ é ¶k ù ê(n + e t ) ú ¶y ë ¶y û y =0 (Рівняння 48) де перший член відображає в'язку дисипацію, і другий - поглинання енергії в'язкопружним матеріалом. Для твердої поверхні на стінці немає поглинання енергії і другий член дорівнює нулю. Поглинання турбулентної ¶k et ¶y y = 0 енергії покриттям еквівалентне - p' n' , i може бути апроксимоване виразом , що є дифузійним потоком енергії через границю і характеризується за допомогою градієнтного механізму для турбулентної дифузії. Цей вираз динамічної граничної умови сумісний з методологією переносу напружень Рейнольдса для замикання моделі турбулентності. Рівняння 13,14, 15a-15d, і 16 розв'язуються для компонентів середньої швидкості, нормальних і зсувних напружень Рейнольдса і дисипації енергії при заданих динамічних і кінематичних граничних умовах (Рівняння 44-48), які спираються на розв'язок в'язкопружної задачі (який описано в наступному розділі). Ця задача розв'язується чисельно, використовуючи кінцево-різницеві апроксимації параболічних рівнянь. Опір тертя тіла з в'язкопружним покриттям обчислюється як інтеграл напруження зсуву на стінці tw по всій поверхні тіла, де: tw = m ¶k ¶y (Рівняння 49) y=0 для двовимірного тіла, і де m=rn - динамічна в'язкість. Порівняння результатів з обчисленими для твердого тіла такої ж геометрії при таких же граничних умовах дає оцінку очікуваного зниження опору тертя. Щоб знизити опір тертя, необхідно мінімізувати амплітуди коливання поверхні і забезпечити максимальний потік турбулентної енергії з потоку рідини в покриття - p' n' . Якщо амплітуди коливання поверхні x 2+ не перевищують товщину в'язкого підшару, що у загальному випадку: yu y + = * 1 у записі комплексного модуля зсуву в Рівнянні (76). Dmax= ( ) ( ) é wt 2 N wtj j m (w) = m0 + å m j ê +i ê 1 + wtj 2 1 + wtj j=1 ë ù ú 2ú û ( ) (Рівняння 76) Представлення Havriliak-Negami (ΗΝ) для комплексного модуля зсуву дано в Рівнянні 77. Це - більш складне рівняння, часто більш придатне для опису реальних матеріалів: m - m¥ 1 = (Рівняння 77) m0 - m ¥ a HN b HN 1 + (iwtHN ) Для матеріалу типу ΗΝ, модуль зсуву якого виражається у формі Рівняння (77), m ¥ - це граничний високочастотний модуль, a a HN і βNH - константи. Для полімерних матеріалів, використовуваних" для покриттів, що знижують опір, K(w ) є практично константою зі значенням приблизно 1x108Ра. [ ] Рекомендується спочатку визначати оптимальний матеріал типу SRT, а потім вибирати матеріал на підставі ΗΝ моделі з властивостями, що можуть бути отримані при існуючих способахах хімії полімерів. SRT матеріал можна адекватно характеризувати товщиною матеріалу Н, густиною rs, статичним модулем зсуву m 0, динамічним модулем зсуву m s і часом релаксації t. Придатною густиною rs для в'язкопружного матеріалу є густина у межах 10% густини води. Для SRT матеріалу початковим наближенням для статичного модуля зсуву матеріалу m 0 є: (Рівняння 78) m 0=rsC2 грунтуючись на критерії, що швидкість зсувної хвилі в матеріалі приблизно дорівнює фазовій швидкості енергонесучих збурень С. Ця фазова швидкість С вважається рівною 0.8 значення швидкості у вільному потоці U (Рівняння 42). Якщо конвективна швидкість перевищує швидкість зсувної хвилі, виникає нестійкість і на поверхні матеріалу виникають великі хвилі, що приводить до підвищення опору покриття. ms m Початковий вибір товщини Η для ізотропних матеріалів, для яких 0 > 1, це: 3C H= (Рівняння 79) we ms m і для ізотропних матеріалів з низькою в’язкістю, коли 0 < 1: 5C H= (Рівняння 80) we Бажана оптимальна товщина покриття може бути більшою, ніж практично здійсненна для конкретного випадку застосування. Хоча ізотропні покриття, рекомендовані з Рівнянь 79-80 можуть усе ще бути ефективними,анізотропні покриття, що більш тверді в нормальному напрямку, ніж у поздовжньому, можуть давати таку ж ефективність при значно меншій товщині. При даних значеннях Η, m 0, і rs, ВП задача, виражена в Рівняннях (57) і (58), розв'язується чисельно для матриці значень ts і m s (тобто, для різних значень комплексного модуля зсуву ) і діапазону хвильових чисел. Хвильове число, що відповідає максимуму турбулентної енергії в пограничному шарі, дорівнює: w ae = e (Рівняння 81) C де частота w e для максимальних енергонесучих збурень оцінюється Рівнянням (41). Розрахунки дають амплітуди зсуву і потік турбулентної пульсаційної енергії в покриття. Найкраща комбінація властивостей для SRT матеріалу досягається тоді, коли зсув поверхні під дією реального навантаження (Рівняння (61)) менший, ніж товщина в'язкого підшару. і коли потік енергії в покриття (Рівняння (57)) максимальний. Більш того, бажано дотримувати цей критерій для діапазону частот від приблизно одного розряду нижче до одного розряду вище енергонесучої частоти w e. Після того, як знайдено оптимальні значення ts і m s для заданого набору значень Н, m 0 і rs, обчислення повторюються для трохи інших значень товщини Η і статичного модуля m 0. З цих розрахунків вибирають оптимальний для заданої конфігурації й умов потоку набір параметрів SRT матеріалу (Η, m 0, rs, ts and m s). Комплексні модулі зсуву реальних полімерних матеріалів, таких як поліуретани і силікони, і які є кандидатами для в'язкопружних покриттів, не можуть бути адекватно описані SRT представленням. Більш складні MRT і ΗΝ описи модуля зсуву вимагають безліч констант і менше підходять для чисельної параметричної оцінки. Тому результати для SRT матеріалів використовуються для вибору матеріалівкандидатів, таких як описувані HN-фомулюванням (Рівняння (79)), які легше виготовити практично. Як напрямок пошуку, бажано домагатися збігу кривих модуля зсуву шуканого SRT матеріалу і HN матеріалу (значення і нахилу) на діапазоні частот на один розряд нижче і вище w e, причому найбільш важливим є збіг безпосередньо у районі w e. Для того, щоб сконструювати багатошарове ізотропне покриття, задаються властивості комплексного модуля зсуву, густина і товщина кожного шару, і накладаються умови непрослизання між шарами. Властивості верхнього шару вибираються за методологією для одного шару, а модулі зсуву нижніх шарів будуть послідовно зменшуватися, що оптимально для більш низьких швидкостей вільного потоку. Таким чином, добре сконструйовані багатошарові покриття можуть знижувати опір на діапазоні швидкостей вільного потоку. При розробці анізотропного покриття комплексний модуль зсуву має в нормальному напрямку значення, відмінні від поздовжнього і трансверсального напрямку (надалі називається трансверсально ізотропний). Якщо в'язкопружний матеріал може бути описаний моделлю з одним часом релаксації, то статичний модуль зсуву m 0, динамічний модуль зсуву ms і час релаксації ts будуть мінятися з напрямком, як записано в Рівняннях (82) і (83). Статичний модуль зсуву в нормальному напрямку m 01 буде більше, ніж модуль у поздовжньотрансверсальній площині m 02. Комплексний модуль зсуву в нормальному напрямку виражається як: é (wt )2 wts1 ù s1 +i m1(w) = m01 + m s1 ê ú 2 2 ê1 + (wts1) 1 + (wts1 ) ú û ë (Рівняння 82) а модуль зсуву в поздовжньому і трансверсальному напрямках: é (wt )2 wts2 ù s2 +i m 2 (w ) = m 02 + m s2 ê ú 2 2 ê 1 + (wts 2 ) 1 + (wts 2 ) ú û ë (Рівняння 83) Для в'язкопружного, трансверсально ізотропного матеріалу амплітуди коливання поверхні можуть знижуватися в порівнянні з ізотропним матеріалом, у той час як рівень потоку енергії в матеріал зростає. Таким чином, добре сконструйоване анізотропне покриття буде значно тоншим, ніж ізотропне покриття з тим же рівнем зниження опору. Методологія вибору структури в'язкопружного покриття, що знижує опір Іншим аспектом розробки покриття є вибір внутрішньої структури у в'язкопружному матеріалі. У практичних застосуваннях в'язкопружних покриттів, покриття буде скінченним у довжині, з передньою, задньою і бічною кромками. Кінцеві кромки впливають на ефективність покриття. Добре виконані кромки можуть упорядковувати і стабілізувати поздовжні і трансверсальні вихрові структури в пристінній області потоку і. тим самим, сповільнювати деформацію цих вихрових структур і підтримувати стійкість потоку. Однак неструктуровані кромки можуть підсилювати амплітуду коливання в'язкопружного матеріалу в цій області. Локальна нестійкість може знизити ефективність покриття, тобто, навіть при добре сконструйованому матеріалі вплив кромок може приводити до підвищення опору. Отже, покриття повинне бути структуроване поблизу кромок. Товщина покриття зменшується для мінімізації таких коливань, використовуючи такі способи як твердий клин під покриттям чи інші локалізовані структури біля кромки (фігура 3). Для великих тіл суцільне покриття може бути непрактичним чи складним для виготовлення. Альтернативний дизайн - це кусочно-суцільне покриття, складене зі скінченних сегментів покриття, коли і поздовжні, і трансверсальні кромки цієї системи організовані так, щоб стабілізувати структуру потоку і мінімізувати зворотні ефекти на кромках кожного сегмента. Крім добре застосованих кромок в'язкопружні покриття можуть комбінуватися з поверхневою структурою для посилення стабілізації подовжніх вихрів уздовж довжини покриття, збільшуючи, таким чином, рівень зниження опору за допомогою декількох фізичних механізмів. Структура може включати розміщення риблетів зверху в'язкопружного покриття, чи створення так званих «зворотних» риблетів. В останньому випадку в'язкопружне покриття може бути запресоване над ребрами чи гребенями твердого матеріалу так, що коли рідина обтікає в'язкопружне покриття, формуються структури поздовжніх риблетов. Розміри сегментів і розміри структур усередині покриття вибираються кратними трансверсальному і поздовжньому масштабам у турбулентному потоці біля стінки. Ці масштаби змінюються зі швидкістю тіла, координатою уздовж тіла й у присутності неньютоновських домішків, таких як водні розчини полімерів з високою молекулярною вагою. В'язкопружне покриття цього винаходу не обмежено проілюстрованим конструктивним виконанням. В'язкопружні покриття можуть бути встановлені на тілах різних розмірів і форм, включаючи осесиметричні тіла, а також плоскі пластини. Параметри покриття будуть вибиратися, ґрунтуючись на методології цього винаходу, і можуть включати анізотропні матеріали, де властивості матеріалу (такі як модуль зсуву) у нормальному напрямку відрізняються від властивостей у трансверсальній площині. Структура покриття може бути модифікована біля передньої і задньої кромок як функція конкретної конфігурації. Різні модифікації можуть бути придумані тими, хто одержав достатню кваліфікацію в цьому предметі в результаті читання вищевикладеного, і всі такі модифікації, як очевидно для всякого, хто має звичайну кваліфікацію в предметі, будуть у дусі заявленого винаходу.