Рекурсивний спосіб оптимальної екстраполяції характеристик випадкового нестаціонарного процесу на фоні завад
Номер патенту: 86555
Опубліковано: 10.01.2014
Автори: Андрєєв Володимир Ілліч, Андреєв Олександр Володимирович, Ігнатов Володимир Олексійович
Формула / Реферат
1. Рекурсивний спосіб оптимальної екстраполяції нестаціонарних випадкових процесів (ВНП) на тлі завад, у якому для оптимальної екстраполяції нестаціонарного випадкового процесу на тлі завади використовують метод максимальної правдоподібності, а також декілька попередніх результатів вимірювань зашумленого сигналу з апріорно відомими вірогідними характеристиками (математичними очікуваннями, дисперсіями, кореляційними функціями процесу та завади), що проводять визначення оптимального прогнозованого (екстрапольованого) значення характеристик випадкового нестаціонарного процесу на тлі завад за критерієм мінімуму дисперсії похибки екстраполяції.
2. Спосіб за п. 1, який відрізняється тим, що оптимальна оцінка ![]() для майбутнього моменту часу
для майбутнього моменту часу ![]() екстрапольованого значення випадкового нестаціонарного процесу
екстрапольованого значення випадкового нестаціонарного процесу
![]() , (1)
, (1)
що спостерігають на тлі завади ![]() у два попередні моменти часу
у два попередні моменти часу ![]() ,
, ![]() у вигляді зашумленого сигналу
у вигляді зашумленого сигналу
![]() , (2)
, (2)
де ![]() , детерміновані параметри
, детерміновані параметри ![]() ,
, ![]() задання нелінійності і нестаціонарності випадкового процесу
задання нелінійності і нестаціонарності випадкового процесу ![]() задовольняють умовам:
задовольняють умовам:
![]() ,
, ![]() , (3)
, (3)
коефіцієнти ![]() ,
, ![]() є випадковими незалежними величинами, що мають гауссівські розподіли з математичними очікуваннями і дисперсіями:
є випадковими незалежними величинами, що мають гауссівські розподіли з математичними очікуваннями і дисперсіями:
![]() , (4)
, (4)
заваду (шум) ![]() представляють як випадковий стаціонарний гауссівський сигнал з характеристиками
представляють як випадковий стаціонарний гауссівський сигнал з характеристиками
![]() , (5)
, (5)
визначають за двома попередніми вимірюваннями ![]() та
та ![]() і апріорною інформацією (1) -(5) за формулою непрямих вимірювань першої ітерації [2]:
і апріорною інформацією (1) -(5) за формулою непрямих вимірювань першої ітерації [2]:
![]() , (6)
, (6)
де значення параметрів ![]() ,
, ![]() вибирають оптимальним способом розв'язання задачі оптимізації з використанням класичного методу знаходження мінімуму дисперсії похибки екстраполяції як функції двох змінних
вибирають оптимальним способом розв'язання задачі оптимізації з використанням класичного методу знаходження мінімуму дисперсії похибки екстраполяції як функції двох змінних
3. Спосіб за п. 1, який відрізняється тим, що оптимальна оцінка ![]() для майбутнього моменту часу
для майбутнього моменту часу ![]() екстрапольованого значення випадкового нестаціонарного процесу, що спостерігають на тлі завади
екстрапольованого значення випадкового нестаціонарного процесу, що спостерігають на тлі завади ![]() у два попередні моменти часу
у два попередні моменти часу ![]() ,
, ![]() та отриманій оцінці
та отриманій оцінці ![]() у першій ітерації у вигляді зашумленого процесу, за другою ітерацією визначають оцінку
у першій ітерації у вигляді зашумленого процесу, за другою ітерацією визначають оцінку ![]() майбутнього значення
майбутнього значення ![]() за формулою непрямих вимірювань [4]:
за формулою непрямих вимірювань [4]:
![]() , (7)
, (7)
де ![]() ,
, ![]() ,
, ![]() - параметри трипараметричної оптимізації,
- параметри трипараметричної оптимізації,
для оптимізації оцінки ![]() вибирають середньоквадратичний критерій методу найменших квадратів у вигляді квадрата відстані між
вибирають середньоквадратичний критерій методу найменших квадратів у вигляді квадрата відстані між ![]() та
та ![]() у евклідовому просторі:
у евклідовому просторі:
![]() , (8)
, (8)
в задачі оптимізації використовують класичний метод знаходження мінімуму функції трьох змінних: беруть похідні від ![]() по
по ![]() ,
, ![]() ,
, ![]() та прирівнюють їх до нуля (це є необхідною умовою екстремуму [5]),
та прирівнюють їх до нуля (це є необхідною умовою екстремуму [5]),
підставляють у вираз (8) замість ![]() його значення з (7), тоді отримують:
його значення з (7), тоді отримують:
![]() , (9)
, (9)
беруть похідні від ![]() і прирівнюють їх до нуля:
і прирівнюють їх до нуля:
![]() ; (10)
; (10)
![]() ; (11)
; (11)
![]() ; (12)
; (12)
використовують властивості математичного сподівання для виразів (10), (11), (12) та перемножують складові у фігурних дужках, отримують систему рівнянь у такій формі [4]:
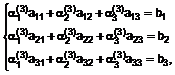 (13)
(13)
де:
![]()
![]()
![]()
![]()
![]()
![]() - математичне сподівання екстрапольованого значення
- математичне сподівання екстрапольованого значення ![]() та його дисперсія
та його дисперсія ![]() , які обчислюють за способом двопараметричної екстраполяції у [2],
, які обчислюють за способом двопараметричної екстраполяції у [2],
вирішують систему рівнянь (13) відносно ![]() ,
, ![]() ,
, ![]() та отримують значення
та отримують значення ![]() ,
, ![]() ,
, ![]() ,
,
тепер розглядають другі похідні від ![]() , отримують наступну матрицю:
, отримують наступну матрицю:
а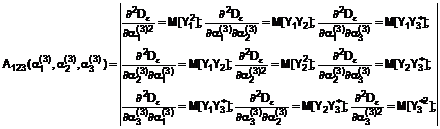 , (14)
, (14)
де ![]() записано для скорочення запису,
записано для скорочення запису,
розглядають достатню умову екстремуму функції трьох змінних [5], квадратична форма від 3-х дійсних змінних ![]() ,
, ![]() ,
, ![]() , де
, де ![]() для матриці других часткових похідних матиме такий вигляд:
для матриці других часткових похідних матиме такий вигляд:
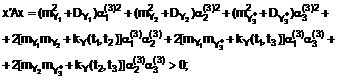 (15)
(15)
де ![]() - матриця других часткових похідних (14);
- матриця других часткових похідних (14);
![]() - матриця-строка;
- матриця-строка;
![]() - матриця-стовпець.
- матриця-стовпець.
4. Спосіб за п. 1, який відрізняється тим, що при оптимальному значенні параметрів ![]() ,
, ![]() ,
, ![]() похибка екстраполяції мінімальна та приймає мінімальне значення за формулою непрямих вимірювань:
похибка екстраполяції мінімальна та приймає мінімальне значення за формулою непрямих вимірювань:
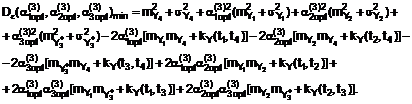 (16)
(16)
5. Спосіб за п. 1, який відрізняється тим, що дисперсію оптимальної оцінки ![]() отримують за формулою непрямих вимірювань:
отримують за формулою непрямих вимірювань:
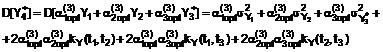 .(17)
.(17)
6. Спосіб за п. 1, який відрізняється тим, що ефективність трипараметричного способу оптимальної екстраполяції оцінюють за формулами непрямих вимірювань:
![]() - відношення сигнал/шум на виході оптимального екстраполятора:
- відношення сигнал/шум на виході оптимального екстраполятора:
![]() , (18)
, (18)
де ![]() - дисперсія випадкового процесу, що спостерігають у момент часу
- дисперсія випадкового процесу, що спостерігають у момент часу ![]() ,
, ![]() - мінімальна дисперсія похибки екстраполяції,
- мінімальна дисперсія похибки екстраполяції,
![]() - відношення дисперсії випадкового процесу, що буде спостерігатися у момент часу
- відношення дисперсії випадкового процесу, що буде спостерігатися у момент часу ![]() , до дисперсії екстрапольованого значення процесу
, до дисперсії екстрапольованого значення процесу ![]()
![]() . (19)
. (19)
Текст
Реферат: Рекурсивний спосіб оптимальної екстраполяції нестаціонарних випадкових процесів (ВНП) на тлі завад, у якому для оптимальної екстраполяції нестаціонарного випадкового процесу на тлі завади використовують метод максимальної правдоподібності, а також декілька попередніх результатів вимірювань зашумленого сигналу з апріорно відомими вірогідними характеристиками (математичними очікуваннями, дисперсіями, кореляційними функціями процесу та завади). В основу побудови корисної моделі поставлено задачу визначення оптимального прогнозованого (екстрапольованого) значення характеристик випадкового нестаціонарного процесу на тлі завад за критерієм мінімуму дисперсії похибки екстраполяції. UA 86555 U (54) РЕКУРСИВНИЙ СПОСІБ ОПТИМАЛЬНОЇ ЕКСТРАПОЛЯЦІЇ ХАРАКТЕРИСТИК ВИПАДКОВОГО НЕСТАЦІОНАРНОГО ПРОЦЕСУ НА ФОНІ ЗАВАД UA 86555 U UA 86555 U 5 10 Корисна модель належить до теорії випадкових процесів та використання цієї теорії для розв'язання прикладних задач надійності, діагностування, контролю якості, обробки сигналів на тлі завад, контролю працездатності та прогнозуванні трафіку обчислювальних мереж, при макропрогнозуванні трендів в економіці при малих обсягах вибірок в часових рядах. Аналогом запропонованого способу є спосіб оптимальної екстраполяції випадкових нестаціонарних сигналів на тлі завад [1], в основу якого поставлено задачу визначення оптимального вагового коефіцієнта opt за критерієм мінімуму дисперсії min D ( ) похибки оптимального прогнозованого (екстрапольованого) значення випадкового нестаціонарного процесу на фоні завад. Оцінку Y3 істинного значення X 3 в момент часу t 3 розглядаємо як лінійну комбінацію (функцію) попередніх значень, що спостерігають Y3 1Y1 2 Y2 , (1) при цьому вважається, що параметри 1 , 2 задовольняють вимозі нормування 1 2 1 , тоді 1 , 2 1 , оцінка 15 20 25 30 35 Y3 Y2 ( Y1 Y2 ) . (2) Цей спосіб отримав назву однопараметричного способу екстраполяції випадкових нестаціонарних процесів на тлі завад. Його недоліком є те, що в деяких випадках параметр може бути від'ємним, а це в свою чергу, може призвести до спотворення результатів екстраполяції. Аналогом запропонованого способу є також спосіб двопараметричної оптимальної екстраполяції випадкових нестаціонарних сигналів на тлі завад [2]. В основу двопараметричного оптимального способу екстраполяції поставлено задачу визначення оптимальних вагових параметрів оптимізації 1opt , 2opt за критерієм мінімуму дисперсії похибки екстраполяції D ( 1, 2 )min випадкового нестаціонарного процесу (ВНП). При вирішенні цієї задачі використовуються такі ж позначення, що і для способу однопараметричної оптимальної екстраполяції. Тоді оптимальне екстрапольоване значення ВНП Y3 приймає вигляд (1). Спосіб двопараметричної екстраполяції позбавлений недоліків однопараметричного способу і має дисперсію похибки екстраполяції на порядок меншу. Прототипом корисної моделі вибрано цифровий оптимальний екстраполятор нестаціонарного трафіку комп'ютерних мереж [3], який на базі способу однопараметричної екстраполяції та при наявності математичної моделі трафіку дозволяє по двох значеннях виміряних його характеристик екстраполювати третє значення. Якщо невідома математична модель трафіку, то використовувати такий екстраполятор неможливо. Для того, щоб було можливо виконувати екстраполяцію характеристик трафіку в реальному часі необхідно розробити спосіб визначення параметрів та прогнозування значень кореляційних функцій випадкових процесів. В основу корисної моделі поставлено задачу визначення оптимізуючих параметрів 1opt , 2opt , 3opt за допомогою яких визначають оптимальне прогнозне (екстрапольоване) значення Y4 на тлі завад по двох попередніх значеннях процесу Y1 , Y2 , що спостерігаються, та екстрапольованому значенню характеристики випадкового нестаціонарного процесу (ВНП) 40 45 50 Y3 , отриманому за двопараметричним способом [2], за критерієм мінімуму дисперсії похибки екстраполяції. В [1], [2] були запропоновані однопараметричний та двопараметричний способи екстраполяції, недоліком яких є те, що вони дозволяють по двох попередніх значеннях процесу, що спостерігається, екстраполювати лише одне, третє значення випадкового нестаціонарного процесу. Запропоновано рекурсивний спосіб, який використовує вірогідну вихідну інформацію, отриману в двопараметричному способі екстраполяції, дозволяє екстраполювати, крім третього Y3 , четверте Y4 значення випадкового нестаціонарного процесу на тлі завад. Розглядають постановку задачі рекурсивного способу оптимальної екстраполяції ВНП на тлі завади, складовою частиною якого є трипараметричний спосіб екстраполяції. Вводять такі основні позначення: X( t ) - випадковий нестаціонарний сигнал, значення якого прогнозуються; ( t ) - випадкова завада, що спотворює дані спостережень; 1 UA 86555 U Y( t ) - випадковий сигнал, реалізація якого спостерігається, t i , i 1, n i - й момент спостереження, 5 Y( t i ) Yi i e - значення Y( t ) в момент часу спостереження t i , Yn1 Y( t n1 ) - значення Y( t ) , що прогнозується (екстраполюється), T t n t1 - інтервал спостереження, t n1 t n - інтервал екстраполяції (прогнозу), M[ Y( t )] m( t ) - математичне сподівання Y( t ) , D[ Y( t )] M[ Y( t ) m( t )]2 - дисперсія Y( t ) , k( t i , t j ) M{[ Y( t i ) m( t i )][ Y( t j ) m( t j )]} - кореляційна функція Y( t ) , 10 k ( t i , t j ) M{[( t i ) m ][ ( t j ) m ]} - кореляційна функція завади ( t ) , M[ ( t )] m ( t ) - математичне сподівання завади ( t ) . На фіг. 1 показані всі основні характеристики і параметри екстраполяції ВНП. Неважко помітити різницю Xn1 від Yn1 та вплив завади ( t ) на характеристики Yn1 . Для спрощення на фіг. 1 показано два спостереження (n=2), в результаті спостереження отримують значення Y1 , 15 20 Y2 замість істинних значень X1 , X 2 , по яких необхідно визначити X 3 , X 4 але насправді оптимально спрогнозувати значення Y3 , Y4 . Задача трипараметричного способу оптимальної екстраполяції розв'язується у такій загальній постановці. Приймаються такі припущення: 1. Відомі результати N попередніх спостережень випадкового нестаціонарного процесу X( t ) на тлі завади ( t ) ; 2. Завада вважається випадковим стаціонарним процесом з апріорно відомими математичними сподіваннями і кореляційною функцією: M[ ( t )] m ( t ) ; (3) K ( t ) 2 ( t ) , (4) 25 де: 2 - дисперсія (потужність) завади, (t ) - нормована кореляційна функція завади; t t 2 t1 3. Математичне сподівання ВНС M[ X( t )] , дисперсія D[ X( t )] і кореляційна функція K X ( t i , t j ) вважаються апріорно відомими; 4. Екстрапольоване значення ВНП Y ( t 3 ) розглядається як n-параметрична функція N 30 значень Y( t1 ) , Y( t N ) ВНП, що спостерігається (N n) ; Y ( t N1 ) YN1[ Y( t1 ), Y( t 2 ), Y( t N ),1, n ] , (5) 35 де: 1 , n - параметри оптимізації вибору Y ( t N1 ) за певним критерієм. 5. В ролі критерію оптимізації виступає показник точності екстраполяції, який при використанні методу максимальної правдоподібності приводить до такого оптимального вибору параметрів і критеріїв оптимізації: D1min ( 1opt , nopt ) min D1( 1opt , 2opt ) min M[ Y ( t N1 ) YN1 ]2 , (6) 1,n 1,n Dn min ( 1opt , nopt ) min Dn ( 1opt , 2opt ) min M[ Y ( t N1 ) YN1 ]2 . (7) 1,n 1,n Операції пошуку максимально точних екстрапольованих значень (6), (7) дозволяють знайти оптимальні значення параметрів 1 , n : 40 1opt argmin D1(1 ) , (8) 1 2opt argmin D2 ( 2 ) , (9) 2 nopt arg min Dn (n ) . (10) n 45 При цих припущеннях загальна постановка задачі оптимальної екстраполяції має наступний вигляд. Відомі наступні дані: 2 UA 86555 U 5 10 1. Апріорна інформація щодо вірогідних характеристик X( t ) . 2. Апріорна інформація щодо вірогідних характеристик ( t ) . 3. Аналітична форма процесу Y( t ) Y[ X( t ),( t )] . (11) 4. Використовуються критерії максимальної точності екстраполяції (6), (7). 5. Використовується класичний метод пошуку координат екстремуму функції n змінних, вирішуючи систему рівнянь n-го порядку. Необхідно довизначити апріорну інформацію і застосувати класичний метод пошуку координат екстремумів (6), (7) і знайти: 1. Оптимальні значення ( 13 ) , ( 3 ) , ( 3 ) , opt 2 opt 3 opt де (3 ) вказує на те, що ці параметри визначаються для способу трипараметричної екстраполяції. 2. Мінімальні значення параметра D ( 1opt , 2opt , 3opt )min 15 20 25 30 3. Вибрати критерії ефективності екстрапольованого значення Yopt ( t 4 ) отриманих способів і алгоритмів оптимізації 4. Виконати порівняльну оцінку ефективності способів оптимальної екстраполяції ВНП. Зрозуміло, що задача оптимальної екстраполяції ВНП в умовах, коли спостерігають N1 значень, прогнозують N2 значення, в такій загальній постановці є дуже складною, і повинна розв'язуватись за методом математичної індукції. Враховуючі нестаціонарність випадкового процесу нашою задачею є розв'язання задачі трипараметричної оптимальної екстраполяції при N1=2, N2=2. Тому в способі вирішують загальну задачу оптимальної екстраполяції ВНП, виконують конкретизацію вихідних даних для способу трипараметричної оптимальної екстраполяції [4] для ( випадку n=3, коли використовуються три параметри оптимізації 13 ) , ( 3 ) , ( 3 ) і, відповідно, opt 2 opt 3 opt ( Y4 opt Y4 ( Y1, Y2 , Y3 opt , 13 ) , ( 3 ) , ( 3 ) ) . 2 3 В рекурсивному способі оптимальної екстраполяції ВНП на тлі завад передбачають виконання декількох ітерацій, в результаті яких обчислюють декілька значень величини Y1,..., Y4 , , що спостерігають. Перша ітерація. Це по суті двопараметричний спосіб екстраполяції, який розглядають в [2], де задача екстраполяції полягає в тому, щоб у найкращий спосіб по значеннях Y1 і Y2 , що спостерігаються, отримати оцінку Y3 майбутнього значення Y3 (1). Друга ітерація. По значеннях Y1 і Y2 , що спостерігають, та отриманій оцінці Y3 визначають оцінку Y4 майбутнього значення Y4 . 35 ( Y4 13 ) Y1 ( 3 ) Y2 , ( 3 ) Y3 , (12) 2 3 ( де 13 ) , (23 ) , ( 3 ) - параметри трипараметричної оптимізації. 3 Основні характеристики і параметри типараметричного способу наведені на фіг 1. З першої ітерації використовують екстрапольоване значення випадкового процесу Y3 , його D[ Y3 ] , кореляційні функції k y ( t1, t 2 ) , k y ( t1, t 3 ) , k y ( t 2 , t 3 ) . Решта параметрів, необхідних для трипараметричного способу, обчислюють нижче. Вводять основні позначення випадкових величин [2], що екстраполюються, їх вірогідні параметри та набір апріорної інформації про випадковий нестаціонарний процес. На основі цієї інформації розроблюють спосіб трипараметричної оптимальної екстраполяції випадкових нестаціонарних процесів на тлі завад, отримують математичні вирази для оптимальної екстраполяції наступного значення Y4 та його вірогідних параметрів. В другій ітерації способу використовують припущення (1, 3, 4, 5), описані вище. Оцінку Y4 істинного значення Y4 в момент часу t 4 розглянемо як лінійну комбінацію попередніх значень, що спостерігаються (12). Таким чином, для оптимізації оцінки Y4 вибирають критерій оптимізації такий же як в [2] і дисперсію 40 45 50 ( використовують 13 ) , (23 ) , ( 3 ) як керовані змінні оптимізації. 3 3 UA 86555 U Використовують середньоквадратичний критерій методу найменших квадратів у вигляді квадрата відстані між Y4 та Y4 у евклідовому просторі: 5 10 D( ) M[( Y4 Y4 )2 ] . (13) Для розв'язання задачі оптимізації враховують співвідношення для характеристик випадкових процесів, що спостерігають, зі способу [2]. В задачі оптимізації використовують класичний метод знаходження мінімуму функції трьох ( змінних. Беруть похідні від D( ) по 13 ) , (23 ) , ( 3 ) , та прирівнюють їх до нуля (це є необхідною 3 умовою екстремуму [5]): D D D 0; 0; 0; (3) (3) 1 2 ( 3 ) 3 враховують те, що другі похідні мають такий вигляд: 2D ( 13 ) 2 ; 2D ( 13 ) ( 3 ) 2 2D ( ( 3 ) 13 ) 2 2D ( ( 3 ) 13 ) 3 ; ; ; 2D ( 13 ) ( 3 ) 3 2D ( 3 ) ( 3 ) 2 3 2D ( 3 ) ( 3 ) 3 2 ; ; 2D ( 3 ) 2 2 2D ( 3 ) 2 3 ; ; ; ( де D D ( 13 ) , ( 3 ) , ( 3 ) ) записано для скорочення запису, 2 3 15 ( ( вирішують систему рівнянь третього порядку відносно 13 ) , (23 ) , ( 3 ) , отримують 13 ) , opt 3 (3) , (3) . 2 opt 3 opt Підставляють у вираз (13) замість Y4 його значення з (12). Тоді отримують: ( ( D ( 13 ) , ( 3 ) , ( 3 ) ) M[( Y4 13 ) Y1 ( 3 ) Y2 ( 3 ) Y3 )2 ] . (14) 2 3 2 3 ( Беруть похідні від D ( 13 ) , ( 3 ) , ( 3 ) ) і прирівнюють їх до нуля: 2 3 20 ( D ( 13 ) , ( 3 ) , ( 3 ) ) 2 3 1 ( D ( 13 ) , ( 3 ) , ( 3 ) ) 2 3 2 ( M{2( Y4 13 ) Y1 ( 3 ) Y2 ( 3 ) Y3 )( Y1 )} 0 ; (15) 2 3 ( M{ 2( Y4 13 ) Y1 ( 3 ) Y2 ( 3 ) Y3 )( Y2 )} 0 ; (16) 2 3 ( D ( 13 ) , ( 3 ) , ( 3 ) ) 2 3 25 ( M{ 2( Y4 13 ) Y1 ( 3 ) Y2 ( 3 ) Y3 )( Y3 )} 0 ; (17) 2 3 3 Використовують властивості математичного сподівання для виразів (15), (16), (17) та перемножуючи складові у фігурних дужках, отримують: ( 2 M[ 13 ) Y1 ( 3 ) Y1Y2 ( 3 ) Y1Y3 Y1Y4 ) 0 ; (18) 2 3 ( ( 2 M[ 13 ) Y1Y2 13 ) Y2 ( 3 ) Y2 Y3 Y2 Y4 ) 0 ; (19) 3 ( M[ 13 ) Y1Y3 ( 3 ) Y2 Y3 ( 3 ) Y3 2 Y3 Y4 ) 0 . (20) 2 3 2 У системі рівнянь (18-20) замінюють математичні сподівання M[ Y1 ] , M[ Y1Y2 ] , M[ Y1Y3 ] , 2 M[ Y1Y4 ] , M[ Y2 ] , M[ Y2 Y3 ] , M[ Y2 Y4 ] , M[ Y3 2 ] , M[ Y3 Y4 ] , їх значеннями та отримують [4]: 30 ( 3 ) [m 2 D Y ] ( 3 ) [m Y m Y k Y ( t1, t 2 )] ( 3 ) [m Y m k Y ( t1, t 3 )] m Y m Y k Y ( t1, t 4 ) Y1 2 3 Y3 1 1 2 1 1 4 1 (3) (3) 2 (3) 1 [m Y1 m Y2 k Y ( t1, t 2 )] 2 [m Y2 D Y2 ] 3 [m Y2 m Y3 k Y ( t 2 , t 3 )] m Y2 m Y4 k Y ( t 2 , t 4 ) (21) ( 13 ) [m Y1 m Y k Y ( t1, t 3 )] ( 3 ) [m Y2 m Y k Y ( t 2 , t 3 ) ( 3 ) [m 2 D Y ] m Y m Y4 k Y ( t 3 , t 4 ). 2 3 Y3 3 3 3 3 Систему рівнянь (21) записують у такій формі: 4 UA 86555 U ( 13 )a11 ( 3 )a12 ( 3 )a13 b1 2 3 (3) 1 a 21 ( 3 )a 22 ( 3 )a 23 b 2 (22) 2 3 (3) (3) (3) 1 a 31 2 a 32 3 a 33 b 3 , де: a11 m21 DY1 ;a12 mY1mY2 k Y ( t1, t 2 );a13 mY1mY k Y ( t1, t 3 ); Y 3 a21 mY1mY2 k Y ( t1, t 2 );a22 m2 2 Y 5 DY2 ;a22 mY2 mY k Y ( t 2 , t 3 ); 3 a31 mY1mY k Y ( t1, t 3 );a32 mY2 mY k Y ( t 2 , t 3 );a33 m2 DY ; Y 3 3 3 a31 mY1mY k Y ( t1, t 3 );a32 mY2 mY k Y ( t 2 , t 3 );a33 m2 Y3 3 3 3 DY ; 3 b1 m Y1m Y4 k Y ( t1, t 4 );b 2 m Y2 m Y4 k Y ( t 2 , t 4 );b 3 m Y m Y4 k Y ( t 3 , t 4 ); 3 ( mY 12) mY1 ( 2) mY2 M[ Y3 ] - математичне сподівання екстрапольованого значення opt 2opt 3 Y3 та його дисперсія D Y , які обчислюють за способом двопараметричної екстраполяції у [2]. 3 10 ( ( Вирішують систему рівнянь (22) відносно 13 ) , (23 ) , ( 3 ) та отримують значення 13 ) , opt 3 (3) , (3) . 2 opt 3 opt ( Тепер розглядають другі похідні від D ( 13 ) , ( 3 ) , ( 3 ) ) , отримують наступну матрицю: 2 3 2D ( 13 )2 ( A 123 ( 13 ) , ( 3 ) , ( 3 ) ) 2 3 2 M[ Y1 ]; 2D ( ( 3 ) 13 ) 2 2D ( ( 3 ) 13 ) 3 15 2D ( 13 ) ( 3 ) 2 M[ Y1Y2 ]; M[ Y1Y3 ]; M[ Y1Y2 ]; 2D ( 3 )2 2 2 M[ Y2 ]; 2D ( 3 ) ( 3 ) 3 2 2D ( 13 ) ( 3 ) 3 2D ( 3 ) ( 3 ) 2 3 M[ Y2 Y3 ]; M[ Y1Y3 ]; M[ Y2 Y3 ]; 2D ( 3 )2 3 M[ Y3 2 ]; ( де D D ( 13 ) , ( 3 ) , ( 3 ) ) записано для скорочення запису. 2 3 Розглядають достатню умову екстремуму функції трьох змінних [5]. Квадратична форма від 3-х дійсних змінних 1 , 2 , 3 де n=3 для матриці других часткових похідних матиме такий вигляд: ( xAx (m 21 D Y1 )13 )2 (m 2 2 D Y2 ) ( 3 )2 (m 2 D Y ) ( 3 )2 Y Y 2 3 Y 3 ( 2[m Y1 m Y2 k Y ( t1, t 2 )]13 ) ( 3 ) 2 3 ( 2[m Y1 m Y k Y ( t1, t 3 )]13 ) ( 3 ) (24) 3 3 2[m Y2 m Y k Y ( t 2 , t 3 )] ( 3 ) ( 3 ) 0; 2 3 3 20 ( де A 123 ( 13 ) , ( 3 ) , ( 3 ) ) - матриця других часткових похідних (23); 2 3 x [k ] - матриця-строка; x {i } - матриця-стовпець. ( При оптимальному значенню параметрів 13 ) , (23 ) , ( 3 ) похибка екстраполяції мінімальна 3 та приймає мінімальне значення: ( ( D ( 13 ) , ( 3 ) , ( 3 ) )min m 2 4 2 4 13 )2 (m 21 21 ) ( 3 )2 (m 2 2 2 2 ) Y Y Y Y Y Y opt 2 opt 3 opt opt 2 opt ( ( 3 )2 (m 2 2 ) 213 ) [m Y1 m Y4 k Y ( t1, t 4 )] 2 ( 3 ) [m Y2 m Y4 k Y ( t 2 , t 4 )] 3 opt opt 2 opt Y Y 3 2 ( 3 ) 3 opt 25 3 ( [m Y m Y4 k Y ( t 3 , t 4 )] 213 ) ( 3 ) [m Y1 m Y2 k Y ( t1, t 2 )] opt 2 opt 3 ( 213 ) ( 3 ) opt 3 opt [m Y1 m Y k Y ( t1, t 3 )] 2 ( 3 ) ( 3 ) [m Y2 m Y k Y ( t 2 , t 3 )]. 2 opt 3 opt 3 Дисперсію оцінки D[ Y4 ] ( D[ 13 ) Y1 opt Y4 3 отримують за наступною формулою: ( 3 ) Y2 2 opt ( 213 ) ( 3 ) k Y ( t1, t 2 ) opt 2 opt ( ( 3 ) Y3 ] 13 ) 21 ( 3 ) 2 2 ( 3 ) 2 3 opt opt Y 2 opt Y 3 opt Y ( 213 ) ( 3 ) k Y ( t1, t 3 ) opt 3 opt 3 2 ( 3 ) ( 3 ) k Y ( t 2 , t 3 ) 2 opt 3 opt 5 (26) (25) UA 86555 U Ефективність трипараметричного способу оптимальної екстраполяції формулами: h1 - відношення сигнал/шум на виході оптимального екстраполятора: оцінюють за де D[ Y4 ] - дисперсія випадкового процесу, що спостерігають у момент часу t4 , h1 5 D[ Y4 ] (3) D ( 1opt , ( 3 ) , ( 3 ) )min 2 opt 3 opt , (27) ( D ( 13 ) , ( 3 ) , ( 3 ) )min - мінімальна дисперсія похибки екстраполяції. opt 2 opt 3 opt h 2 - відношення дисперсії випадкового процесу, що буде спостерігатися у момент часу t 4 , до дисперсії екстрапольованого значення процесу D[ Y4 ] h2 10 15 D[ Y4 ] . (28) D[ Y4 ] На фіг. 2 показана узагальнена структурна схема способу. Спосіб реалізується наступним чином. Цикл вимірювань починають з того, що з об'єкта вимірювання ОВ (блок 1) за сигналами управління СУ блока 2 управління та синхронізації БУС у моменти часу t1 , t 2 вимірюють значення характеристик ВНП Y1 , Y2 (блок 4), що спостерігають, і подають на блок обчислення БО (блок 5). Крім того, на БО з бази даних також подають апріорно відомі параметри процесу і 2 2 завади: m0 , m1 , 0 , 1 , 2 , , де m0 , m1 - математичні сподівання параметрів a 0 , a 1 ; 2 2 0 , 1 - середні квадратичні відхилення параметрів a 0 , a 1 ; 2 - середнє квадратичне відхилення завади, - інтервал кореляції завади [2]. 20 25 30 35 40 За наступною командою БУС БО виконує обчислення за формулами непрямих вимірювань двопараметричного способу [2], що в даному випадку відіграють роль операторних рівнянь роботи певних функціональних пристроїв оптимального екстраполятора. Після закінчення обчислень за двопараметричним способом (першої ітерації) БО подає команду БУС видати результати обчислень у вигляді параметрів 1opt , 2opt , D ( 1opt , 2opt )min , D[ y ] , h1 , h 2 , h 3 , 3 Y3 , Y3 на блок 6 - блок відображення результатів БВР у даному циклі. Одночасно з відображенням результатів першої екстраполяції ці параметри запам'ятовують в базі даних (блок 3), для того, щоб після декількох циклів можна було б побудувати графіки зміни цих параметрів. Далі необхідно виконати другу ітерацію трипараметричного способу. За наступною командою БУС БО виконує обчислення за формулами непрямих вимірювань другої ітерації трипараметричного способу (14-28), що в даному випадку відіграють роль операторних рівнянь роботи певних функціональних пристроїв оптимального екстраполятора. Після закінчення обчислень за другою ітерацією трипараметричного способу БО подає команду БУС видати ( ( результати обчислень у вигляді параметрів 13 ) , ( 3 ) , ( 3 ) , D ( 13 ) , ( 3 ) , ( 3 ) )min , D[ y ] , 4 opt 2 opt 3 opt opt 2 opt 3 opt h1 , h 2 , Y4 , Y4 на блок 6 - блок відображення результатів БВР у даному циклі. Одночасно з відображенням результатів другої екстраполяції ці параметри запам'ятовують в базі даних (блок 3), для того, щоб після декількох циклів можна було б побудувати графіки зміни цих параметрів. Як випливає з принципу роботи структурної схеми способу, вхідні сигнали Y1 , Y2 , t1 , t 2 , t1 , 2 2 , m0 , m1 , 0 , 1 , 2 , згідно з операторними рівняннями (14-28) перетворюють у вихідні ( ( сигнали Y3 , Y3 , Y4 , Y4 , 13 ) , ( 3 ) , ( 3 ) , D ( 13 ) , ( 3 ) , ( 3 ) )min , D[ y ] , h1 , h 2 . Тому цей 4 opt 2 opt 3 opt opt 2 opt 3 opt спосіб названо способом трипараметричної оптимальної екстраполяції випадкових ( нестаціонарних сигналів на тлі завад, він дозволяє оптимально обчислювати параметри 13 ) , opt ( 3 ) , ( 3 ) , екстраполювати значення Y3 , Y4 з дисперсіями D[ y ] D[ Y3 ] , D[ y ] D[ Y4 ] і 3 4 2 opt 3 opt 45 ( D ( 13 ) , ( 3 ) , ( 3 ) )min . opt 2 opt 3 opt 6 UA 86555 U Приклад. Для того, щоб перевірити дієздатність та ефективність способу був проведений експеримент методом статистичного імітаційного моделювання (СІМ). В експерименті була поставлена задача - методом СІМ в системі MathCAD встановити часові залежності наступних випадкових величин: X i , Yi (і=1…15), оптимального екстрапольованого значення Y4 , a також 5 ( ( значення 13 ) , ( 3 ) , ( 3 ) , D ( 13 ) , ( 3 ) , ( 3 ) )min , D[ y ] , h1 , h 2 , h 3 для інтервалу кореляції 4 opt 2 opt 3 opt opt 2 opt 3 opt завади 0,25 с. Апріорними даними для МСІМ вибрані такі значення величин: t1 6 с; t 2 10 с - часові відліки вимірювання параметрів X i і Yi ; t 3 12 с - момент часу для екстраполяції значення Y3 ; t 4 14 с - момент часу для екстраполяції значення Y4 ; 10 15 m0 1B ; 0,02B / c - математичні очікування параметрів a 0 , a 1 незалежних випадкових величин, що мають гауссівський розподіл, 0 0,3 B , 1 0,002 B - їх середньоквадратичні відхилення; 0,01B - середньоквадратичне відхилення завади; 0,5 - коефіцієнт нелінійності. За допомогою стандартної функції MathCAD rnorm {n,M, y } , де число реалізацій вибране n 1; M - математичне очікування; y i - середньоквадратичне відхилення НВС, обчислюються значення коефіцієнтів a 0 і a 1 і п'ятнадцять значень завади . В табл.1 показано результати експерименту. На фіг. 3 відображають графіки X( t ) , Y( t ) та 20 Yopt( t3) та Yopt( t 4) , де Yopt( t3) відображає на графіку Y3 , а Yopt ( t 4 ) Y4 . На фіг 4, 5, 6 відображають графіки залежності D f (1 ) , при 2opt , 3opt const ; D f ( 2 ) , при 1opt , 3opt const ; D f (3 ) , при 1opt , 2opt const відповідно. Таблиця 1 Результати експерименту X1 0,763763 Y3 0,771722 Y4 0,793082 25 30 X2 0,778081 X4 0,789719 2opt 0,593577 Y1 0,779228 3opt 0,03435 Y2 0,782672 Y4 0,770553 X3 0,784143 1opt 0,386778 D[ Y3 ] 0,091996 D[ Y4 ] 0,131702 h1 511,76122 h2 0,684547 D ( 1 2 3 )min 0,000176 Y4 0,789453 Аналіз результатів експерименту показав працездатність і високу ефективність способу за Фіг. 2. За результатами експерименту можна зробити такі висновки: 1. Показник ефективності оптимальної екстраполяції h1 показує, що оптимальна екстраполяція забезпечує достатньо високу точність - дисперсія похибки (шумів) екстраполяції в 511 разів менше дисперсії самого ВНП. 2. В результаті оптимальної екстраполяції значення Y4 для моменту часу t 4 14 c знаходиться ближче до значення X 4 , ніж значення Y4 (дивись графік Фіг. 3). ( 3. Графіки Фіг.4-Фіг.6 показують, що дисперсії D ( 13 ) , ( 3 ) , ( 3 ) )min мають мінімум при opt 2 opt 3 opt 35 40 ( значеннях 13 ) , ( 3 ) , ( 3 ) . opt 2 opt 3 opt Наведені результати експерименту наглядно ілюструють новизну, корисність та високу ефективність способу, що пропонують. Список використаних джерел: 1. Пат. на корисну модель 55212 Україна, МПК(2009) G01S 7/36, G06C 17/00. Спосіб оптимальної екстраполяції випадкових нестаціонарних сигналів на тлі завад / В.О. Ігнатов, О.В. Андреев, М.М. Гузій, В.І. Андреев; заявник та патентовласник Національний авіаційний університет. - № u201006043; Заявл. 19.05.2010, опубл. 10.12.2010, Бюл. № 23. - 16 с. 2. Пат. на корисну модель 60390 Україна, МПК G06G 7/30(2006.01), G05B 13/02(2006.01), G03B 15/02(2006.01). Цифровий оптимальний екстраполятор нестаціонарного трафіку 7 UA 86555 U 5 10 комп'ютерних мереж / М.М. Гузій, В.О. Ігнатов, О.В. Андреев, B.I. Андреев; Заявник та патентовласник Національний авіаційний університет. - № u201006549; Заявл. 28.05.2010; опубл. 25.06.2011, Бюл. № 12. - 12 с 3. Пат. на корисну модель 62878 Україна, МПК(2011.01) G06C 3/00, G01S 17/00 Спосіб двопараметричної оптимальної екстраполяції випадкових нестаціонарних сигналів на тлі завад / В.О. Ігнатов, І.А. Жуков, О.В. Андреев, B.I. Андреев; Заявник та патентовласник Національний авіаційний університет. - № u201014719 заявл. 08.12.2010; опубл. 26.09.2011, Бюл. № 18. - 16 с. 4. Андреев О.В. Трипараметричний метод оптимальної екстраполяції випадкових нестаціонарних сигналів на тлі завад / Андреев О.В. // Сучасний захист інформації: зб. наук. Праць. - К.: ДУІКТ, 2012. - № 1. - С. 76-86. 5. Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1968. - 720 с. 15 ФОРМУЛА КОРИСНОЇ МОДЕЛІ 20 25 1. Рекурсивний спосіб оптимальної екстраполяції нестаціонарних випадкових процесів (ВНП) на тлі завад, у якому для оптимальної екстраполяції нестаціонарного випадкового процесу на тлі завади використовують метод максимальної правдоподібності, а також декілька попередніх результатів вимірювань зашумленого сигналу з апріорно відомими вірогідними характеристиками (математичними очікуваннями, дисперсіями, кореляційними функціями процесу та завади), що проводять визначення оптимального прогнозованого (екстрапольованого) значення характеристик випадкового нестаціонарного процесу на тлі завад за критерієм мінімуму дисперсії похибки екстраполяції. 2. Спосіб за п. 1, який відрізняється тим, що оптимальна оцінка Y3 для майбутнього моменту часу t 3 екстрапольованого значення випадкового нестаціонарного процесу q X( t ) i t i , (1) i 0 30 що спостерігають на тлі завади ( t ) у два попередні моменти часу t1 , t 2 у вигляді зашумленого сигналу Y( t ) X( t ) ( t ) , (2) де q 1, детерміновані параметри 0 , 0 задання нелінійності і нестаціонарності випадкового процесу X( t ) задовольняють умовам: 35 40 0 0 1 , 0 1 2 , (3) коефіцієнти a 0 , a 1 є випадковими незалежними величинами, що мають гауссівські розподіли з математичними очікуваннями і дисперсіями: 2 2 M(a0 ) m0 ;D(a0 ) 0 ;M(a1 ) m1 ;D(a1 ) 1 , (4) заваду (шум) ( t ) представляють як випадковий стаціонарний гауссівський сигнал з характеристиками M[( t )] m 0;M[( t1 ),( t 2 )] k ( t ) , (5) визначають за двома попередніми вимірюваннями Y1 Y( t1 ) та Y2 Y( t 2 ) і апріорною інформацією (1) -(5) за формулою непрямих вимірювань першої ітерації [2]: Y3 1Y1 2 Y2 , (6) 45 де значення параметрів 1 , 2 вибирають оптимальним способом розв'язання задачі оптимізації з використанням класичного методу знаходження мінімуму дисперсії похибки екстраполяції як функції двох змінних 3. Спосіб за п. 1, який відрізняється тим, що оптимальна оцінка Y4 для майбутнього моменту часу t 4 екстрапольованого значення випадкового нестаціонарного процесу, що спостерігають 50 на тлі завади ( t ) у два попередні моменти часу t1 , t 2 та отриманій оцінці Y3 у першій ітерації у вигляді зашумленого процесу, за другою ітерацією визначають оцінку Y4 майбутнього значення Y4 за формулою непрямих вимірювань [4]: 8 UA 86555 U ( Y4 13 ) Y1 ( 3 ) Y2 , ( 3 ) Y3 , (7) 2 3 ( де 13 ) , ( 3 ) , ( 3 ) - параметри трипараметричної оптимізації, 2 3 для оптимізації оцінки Y4 вибирають середньоквадратичний критерій методу найменших квадратів у вигляді квадрата відстані між Y4 та Y4 у евклідовому просторі: 5 D( ) M[( Y4 Y4 )2 ] , (8) в задачі оптимізації використовують класичний метод знаходження мінімуму функції трьох ( змінних: беруть похідні від D( ) по 13 ) , ( 3 ) , ( 3 ) та прирівнюють їх до нуля (це є необхідною 2 3 умовою екстремуму [5]), підставляють у вираз (8) замість Y4 його значення з (7), тоді отримують: 10 ( ( D ( 13 ) , ( 3 ) , ( 3 ) ) M[( Y4 13 ) Y1 ( 3 ) Y2 ( 3 ) Y3 )2 ] , (9) 2 3 2 3 ( беруть похідні від D ( 13 ) , ( 3 ) , ( 3 ) ) і прирівнюють їх до нуля: 2 3 ( D ( 13 ) , ( 3 ) , ( 3 ) ) 2 3 1 ( D ( 13 ) , ( 3 ) , ( 3 ) ) 2 3 2 ( M{2( Y4 13 ) Y1 ( 3 ) Y2 ( 3 ) Y3 )( Y1 )} 0 ; (10) 2 3 ( M{ 2( Y4 13 ) Y1 ( 3 ) Y2 ( 3 ) Y3 )( Y2 )} 0 ; (11) 2 3 ( D ( 13 ) , ( 3 ) , ( 3 ) ) 2 3 15 ( M{ 2( Y4 13 ) Y1 ( 3 ) Y2 ( 3 ) Y3 )( Y3 )} 0 ; (12) 2 3 3 використовують властивості математичного сподівання для виразів (10), (11), (12) та перемножують складові у фігурних дужках, отримують систему рівнянь у такій формі [4]: ( 13 )a11 ( 3 )a12 ( 3 )a13 b1 2 3 (3) (3) (3) 1 a 21 2 a 22 3 a 23 b 2 (13) (3) (3) (3) 1 a 31 2 a 32 3 a 33 b 3 , де: a11 m21 DY1 ;a12 mY1mY2 k Y ( t1, t 2 );a13 mY1mY k Y ( t1, t 3 ); Y 3 20 a21 mY1mY2 k Y ( t1, t 2 );a22 m2 2 DY2 ;a22 mY2 mY k Y ( t 2 , t 3 ); Y 3 a31 mY1mY k Y ( t1, t 3 );a32 mY2 mY k Y ( t 2 , t 3 );a33 m2 DY ; Y 3 3 3 3 a31 mY1mY k Y ( t1, t 3 );a32 mY2 mY k Y ( t 2 , t 3 );a33 m2 DY ; Y 3 3 3 3 b1 m Y1m Y4 k Y ( t1, t 4 );b 2 m Y2 m Y4 k Y ( t 2 , t 4 );b 3 m Y m Y4 k Y ( t 3 , t 4 ); 3 mY 3 25 ( 12) mY1 opt ( 2) mY2 2opt M[ Y3 ] - математичне сподівання екстрапольованого значення Y3 та його дисперсія D Y , які обчислюють за способом двопараметричної екстраполяції у [2], 3 ( ( вирішують систему рівнянь (13) відносно 13 ) , ( 3 ) , ( 3 ) та отримують значення 13 ) , ( 3 ) , opt 2 opt 2 3 (3) , 3 opt ( тепер розглядають другі похідні від D ( 13 ) , ( 3 ) , ( 3 ) ) , отримують наступну матрицю: 2 3 2D ( 13 )2 а ( A 123 ( 13 ) , ( 3 ) , ( 3 ) ) 2 3 2 M[ Y1 ]; 2D ( ( 3 ) 13 ) 2 2D ( ( 3 )13 ) 3 30 2D ( 13 ) ( 3 ) 2 M[ Y1Y2 ]; M[ Y1Y3 ]; M[ Y1Y2 ]; 2D ( 3 )2 2 2 M[ Y2 ]; 2D ( 3 ) ( 3 ) 3 2 2D ( 13 ) ( 3 ) 3 2D ( 3 ) ( 3 ) 2 3 M[ Y2 Y3 ]; ( де D D ( 13 ) , ( 3 ) , ( 3 ) ) записано для скорочення запису, 2 3 9 M[ Y1Y3 ]; M[ Y2 Y3 ]; , (14) 2D ( 3 )2 3 M[ Y3 2 ]; UA 86555 U розглядають достатню умову екстремуму функції трьох змінних [5], квадратична форма від 3-х дійсних змінних 1 , 2 , 3 , де n 3 для матриці других часткових похідних матиме такий вигляд: ( xAx (m 21 D Y1 )13 )2 (m 2 2 D Y2 ) ( 3 )2 (m 2 D Y ) ( 3 )2 Y Y 2 3 Y 3 ( 2[m Y1 m Y2 k Y ( t1, t 2 )]13 ) ( 3 ) 2 2[m Y2 m Y k Y ( t 2 , t 3 )] ( 3 ) ( 3 ) 2 3 3 5 3 ( 2[m Y1 m Y k Y ( t1, t 3 )]13 ) ( 3 ) (15) 3 3 0; ( де A 123 ( 13 ) , ( 3 ) , ( 3 ) ) - матриця других часткових похідних (14); 2 3 x [k ] - матриця-строка; x {i } - матриця-стовпець. ( 4. Спосіб за п. 1, який відрізняється тим, що при оптимальному значенні параметрів 13 ) , ( 3 ) , 2 ( 3 ) похибка екстраполяції мінімальна та приймає мінімальне значення за формулою непрямих 3 10 вимірювань: ( ( D ( 13 ) , ( 3 ) , ( 3 ) )min m 2 4 2 4 13 )2 (m 21 21 ) ( 3 )2 (m 2 2 2 2 ) Y Y Y Y Y Y opt 2 opt 3 opt opt 2 opt ( ( 3 )2 (m 2 2 ) 213 ) [m Y1 m Y4 k Y ( t1, t 4 )] 2 ( 3 ) [m Y2 m Y4 k Y ( t 2 , t 4 )] 3 opt opt 2 opt Y Y 3 2 ( 3 ) 3 opt 3 ( [m Y m Y4 k Y ( t 3 , t 4 )] 213 ) ( 3 ) [m Y1 m Y2 k Y ( t1, t 2 )] opt 2 opt (16) 3 ( 213 ) ( 3 ) [m Y1 m Y k Y ( t1, t 3 )] 2 ( 3 ) ( 3 ) [m Y2 m Y k Y ( t 2 , t 3 )]. opt 3 opt 2 opt 3 opt 3 3 5. Спосіб за п. 1, який відрізняється тим, що дисперсію оптимальної оцінки Y4 отримують за формулою непрямих вимірювань: ( ( D[ Y4 ] D[ 13 ) Y1 ( 3 ) Y2 ( 3 ) Y3 ] 13 ) 21 ( 3 ) 2 2 ( 3 ) 2 opt 2 opt 3 opt opt Y 2 opt Y 3 opt Y 3 15 ( 213 ) ( 3 ) k Y ( t1, t 2 ) opt 2 opt ( 213 ) ( 3 ) k Y ( t1, t 3 ) opt 3 opt .(17) 6. Спосіб за п. 1, який відрізняється тим, що ефективність трипараметричного способу оптимальної екстраполяції оцінюють за формулами непрямих вимірювань: h1 - відношення сигнал/шум на виході оптимального екстраполятора: h1 D[ Y4 ] (3) D ( 1opt , ( 3 ) , ( 3 ) )min 2 opt 3 opt , (18) де 20 2 ( 3 ) ( 3 ) k Y ( t 2 , t 3 ) 2 opt 3 opt D[ Y4 ] випадкового дисперсія ( D ( 13 ) , ( 3 ) , ( 3 ) )min opt 2 opt 3 opt процесу, що спостерігають у момент часу t4 , - мінімальна дисперсія похибки екстраполяції, h 2 - відношення дисперсії випадкового процесу, що буде спостерігатися у момент часу t 4 , до дисперсії екстрапольованого значення процесу D[ Y4 ] h2 D[ Y4 ] D[ Y4 ] . (19) 10 UA 86555 U 11 UA 86555 U Комп’ютерна верстка А. Крулевський Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601 12
ДивитисяДодаткова інформація
Автори англійськоюIhnatov Volodymyr Oleksiiovych, Andreiev Volodymyr Illich, Andreiev Oleksandr Volodymyrovych
Автори російськоюИгнатов Владимир Алексеевич, Андреев Владимир Ильич, Андреев Александр Владимирович
МПК / Мітки
МПК: G01S 7/36, G06C 17/00
Мітки: процесу, нестаціонарного, випадкового, рекурсивний, екстраполяції, характеристик, завад, фоні, спосіб, оптимальної
Код посилання
<a href="https://ua.patents.su/14-86555-rekursivnijj-sposib-optimalno-ekstrapolyaci-kharakteristik-vipadkovogo-nestacionarnogo-procesu-na-foni-zavad.html" target="_blank" rel="follow" title="База патентів України">Рекурсивний спосіб оптимальної екстраполяції характеристик випадкового нестаціонарного процесу на фоні завад</a>
Попередній патент: Триопорне шасі безпілотного літального апарата
Наступний патент: Авіаційний космічний комплекс
Випадковий патент: Установка з вироблення сечовини












