Спосіб безцентрового поздовжнього шліфування циліндричних поверхонь

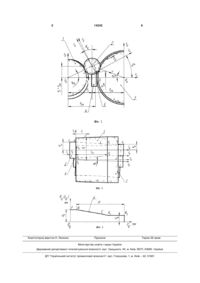
1. Спосіб безцентрового поздовжнього шліфування циліндричних поверхонь, за яким деталь переміщується в осьовому напрямку за рахунок розвороту ведучого круга і базується на ньому та опорному ножі, а шліфування виконується профі 3 14242 4  обертання, яка охоплює параметри заготовки та шліфувального кругів та опорного ножа; n - одидеталі. ничний вектор нормалі до комбінованої поверхні На вказаних Фіг.: 1 - ведучий круг, 2 - обробобертання, яка охоплює параметри заготовки та лювана деталь, 3 - шліфувальний круг, 4 - опорний деталі. ніж, 5 - бокові площини опорного ножа, 6 - твірна Вектор нормалі дорівнює векторному добуткокомбінованої поверхні обертання. ві векторів, дотичних до поверхні деталі. Для їх Для розробки 3D моделей профілювання інвизначення необхідно диференціювати радіус   струментальних поверхонь, при безцентровому вектори rbq , ruq та rнq (2), (3), (4) поверхні деталі поздовжньому шліфуванні циліндричних поверза обома параметрами zq і θq. Для знаходження  хонь зі стабілізацією положення вісі обертання вектора V відносної швидкості необхідно перенедеталей, необхідно радіус-вектор комбінованої  сти радіус-вектор rq (1) поверхні деталі в системи поверхні обертання, яка охоплює параметри заготовки і деталі, перенести у системи координат векоординат ведучого, шліфувального кругів та оподучого, шліфувального кругів та опорного ножа. рного ножа і диференціювати його за часом. Наприклад, конічна зовнішня, з твірною NE К1, Тривимірна геометрична модель шліфувальта циліндрична, з твірною К1К2, поверхні (Фіг.2), які ного круту з урахуванням і-тих точок профілю має відтворюють поверхні заготовки та деталі відповівигляд:   дно, можуть бути описані радіус-вектором rq ru M3 zi M6 u M2 Ri e4 (6)  (Фіг.1): де ru - радіус-вектор точок поверхні шліфува rq M3 (zq ) M6 q M1 Rq zq e4 (1) льного круга; θu - кутовий параметр i-тої точки  профілю круга; Ri - радіус профілю шліфувального де rq - комбінованої поверхні обертання , яка круга в i-тій точці; zi - осьова координата i-тої точки охоплює параметри заготовки і деталі; Rq(zq) - рапрофілю круга. діус заготовки або деталі, що оброблюється, заДля опису 3D моделі процесу зняття припуску лежно від осьової координати zq (Фіг.2) деталі; θq та формоутворення необхідно радіус-вектор точок T кутовий параметр; е4=(0,0,0,1) - радіус-вектор поверхні шліфувального круга перенести у систепочатку координат; М1, ..., М6 - матриці розміром му координат деталі. 4х4 перетворення координат. Тоді радіус-вектор точок поверхні, що обробТоді радіус-вектори ведучого 1, шліфувальноляється, буде мати такий вигляд:   го 3 кругів та опорного ножа 4 будуть мати такий rqu M3 zcu M6 q M5 u M2 ycu M1 xcu ru (7) вигляд:    де rqu - радіус-вектор точок поверхні, що обr M M M y M x M z r (2) bq 6  b 5 b 2 c 1 c 3 c q де rbq - радіус-вектор точок поверхні ведучого круга 1; θb - кутовий параметр, що визначає кутове положення оброблюваної деталі 2 в системі координат ведучого круту 1; ψb - кут перехрещення осей обертання ведучого круга 1 та деталі 2; xc, уc, zc - координати початку координат Оq деталі 2 в системі координат ведучого круга 1.   ruq M6 u M5 u M2 ycu M1 xcu M3 zcu rq (3)  де ruq - радіус-вектор точок поверхні шліфувального круга 3; θu – кутовий параметр, що визначає кутове розташування оброблюваної деталі 2 в системі координат шліфувального круту 3; ψu кут перехрещення осей обертання шліфувального круга 3 та деталі 2; xсu, уcu, zcu - координати початку координат Оq деталі 2 в системі координат шліфувального круга 3.   rнq M2 ун M6 н M2 ycн M1 xcн M3 zcн rq (4)  де rнq - радіус-вектор точок робочої поверхні опорного ножа 4; θн - кутовий параметр, що визначає кутове положення оброблюваної деталі 2 в системі координат опорного ножа 4; ун - координата, яка визначає поточну ширину робочої поверхні опорного ножа 4; хсн, усн, zсн - координати початку координат Оq деталі 2 в системі координат опорного ножа 4. Для знаходження інструментальних поверхонь ведучого і шліфувального кругів та опорного ножа складають рівняння виду:   (5) V n 0  де V - вектор швидкості відносного руху поверхні деталі 2 в системах координат ведучого, робляється; θq - кутовий параметр, що визначає кутове розташування шліфувального круга 3 в системі координат деталі 2. Значення параметрів ψu, хcu, уcu, zcu аналогічні приведеним у рівнянні (3),  а параметра ru - у рівнянні (6). Для визначення лінії контакту шліфувального круга 3 (Фіг.1) та деталі 2 складають рівняння виду:   Vu nu 0 (8)  де Vu - вектор швидкості відносного руху шліфувального круга в системі координат деталі;  nu - одиничний вектор нормалі до поверхні круга.  Методика визначення векторів нормалі nu та  Vu відносної швидкості аналогічна визначенню цих параметрів для ведучого, шліфувального кругів та опорного ножа. Рівняння (7), (8) являють собою 3D модель зняття припуску та формоутворення циліндричних поверхонь при безцентровому поздовжньому шліфуванні. Розроблено новий спосіб безцентрового поздовжнього шліфування циліндричних поверхонь та тривимірні геометричні моделі процесів профілювання кругів, опорного ножа, зняття припуску та формоутворення. Підвищення точності шліфування здійснюється за рахунок компенсації геометричної похибки схеми формоутворення. Це забезпечується профілюванням опорного ножа, ведучого та шліфувального кругів та їх осьовим відносним розташуванням. 5 Комп’ютерна верстка Н. Лисенко 14242 6 Підписне Тираж 26 прим. Міністерство освіти і науки України Державний департамент інтелектуальної власності, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601