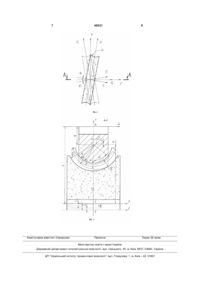
Спосіб шліфування випуклих торових поверхонь зі схрещеними осями інструмента і деталі

Спосіб шліфування випуклих торових поверхонь, згідно з яким деталі надають обертання навколо власної осі, шліфувальному кругу з профілем у вигляді дуги кола надають подачу на 3 40521 роту деталі в процесі обертання, R¶ - відстань від осі обертання деталі до центру профілю. Глобальна система координат верстата OXYZ. Кругу надають поперечну подачу Si(Θ) та одночасно в процесі зняття припуску та формоутворення, круг здійснює поворот відносно прямої, яка перпендикулярна осям заготовки та деталі і яка проходить через вершину торової поверхні і центр профілю осьового переріза деталі. Кут нахилу ψі (Фіг. 2) в кожен момент часу встановлюється таким чином, щоб відхилення профілю випуклої торової поверхні від номіналу було мінімальним, а зняття припуску відбувалось по еквідистантним кривим. Випукла торова поверхня може бути описана радіус-вектором r ¶ = S¶ q ¶ ×R ¶ ×j ¶ ×r ¶ ×e 4 , де r ¶ - радіус-вектор точок випуклої торової поверхні 2; S¶ q ¶ ×R ¶ × j¶ × r ¶ - сферичний модуль, який являє собою матрицю переходу від початкової точки в систему координат деталі; е4= (0,0,0,1)т - радіус-вектор початкової точки. Сферичний модуль являє собою добуток чотирьох однопараметричних матриць S¶ q ¶ ×R ¶ × j¶ ×r ¶ = M6 (q¶ ) × M2 (R¶ ) × M4 (± j¶ ) × M2 (- r ¶ ) , де θ¶ - кут повороту навколо осі O¶Z¶ обертання деталі; R¶ - відстань від центра профілю до осі обертання деталі; φ¶ - кут повороту навколо осі OdYd; ρ¶ - радіус профілю деталі. Особливістю сферичного модуля є наявність двох незалежних кутових параметрів: кута повороту θ¶ навколо осі O¶Z¶ обертання деталі і кут повороту φ¶ початкової точки навколо осі O¶X¶, який може приймати позитивне чи негативне значення в залежності від розташування точки відносно осьової площини. Таким чином, матриці, що складають модуль мають наступний фізичний зміст: æ1 0 0 0 ö ç ÷ ç 0 1 0 r¶ ÷ M2 (- r ¶ ) = ç 0 0 1 0÷ ç ÷ ç0 0 0 1 ÷ è ø – матриця переміщення точки вздовж осі O¶Y¶. Оскільки радіус кривизни профілю деталі залишається незмінним, то параметр у матриці М2 набуває сталого значення, який дорівнює радіусу профілю деталі ρ¶. Знак «-» вказує на те, що радіус задається в протилежному напрямку осі O¶Y¶, тобто поверхня випукла. æ cos j ¶ 0 sin j ¶ 0 ö ç ÷ 0 1 0 0÷ ç M4 (± j ¶ ) = ç - sin j¶ 0 cos j ¶ 0 ÷ ç ÷ ç 0 0 0 1 ÷ – матриця è ø узагальнених поворотів точки відносно осі O¶X¶. Діапазон зміни параметра лежить в межах ±φ¶ mах, 4 які встановлюються максимальним кутом підйому профілю деталі. æ1 0 0 0 ö ç ÷ ç 0 1 0 R¶ ÷ M2 (R¶ ) = ç 0 0 1 0 ÷ ç ÷ ç0 0 0 1 ÷ è ø – матриця переміщення точки вздовж осі O¶Y¶, яка встановлює координату центру профілю деталі. æ cos q¶ - sin q¶ 0 0 ö ç ÷ ç sin q ¶ cos q¶ 0 0 ÷ M6 (q ¶ ) = ç 0 0 1 0÷ ç ÷ ç 0 0 0 1÷ – матриця è ø узагальнених поворотів відносно осі O¶Z¶ обертання деталі. Для профілювання круга необхідно скласти рівняння, що визначає лінію контакту V ¶ × n¶ = 0 де V ¶ - вектор швидкості відносного руху випуклої торової поверхні деталі в системі координат круга; n ¶ - одиничний вектор нормалі до поверхні деталі. Вектор нормалі дорівнює векторному добутку векторів дотичних до поверхні деталі. Для їхнього визначення необхідно диференціювати радіус r ¶ (q ¶ , j¶ ) вектор поверхні деталі по обох параq ¶ і j ¶ . Для знаходження вектора V ¶ метрах відносної швидкості необхідно перенести радіус r (q ,j ) вектор ¶ ¶ ¶ поверхні деталі в систему координат круга і диференціювати його за часом. Переведення радіус-вектора деталі в систему координат круга відбувається через матрицю переходу Мі¶, яка складається з двох сферичних модулів r i ¶ = Mi¶ × r ¶ Mi¶ = Sф i× y × So q y i де: Sф i×y qi c c i , - модуль формоутворення інстру o Sy i - модуль кутової орієнтації інструмента мента; відносно деталі. Модуль формоутворення складається з добутку двох матриць S фi×y = M6 (qi ) × M2 (yc ) q i c де: θi - кут повороту системи координат деталі відносно осі обертання інструмента; ус - відстань між осями обертання інструмента 1 і деталі 2. Модуль орієнтації представлений матрицею відносних поворотів So = M5 (y i ) y i , де: ψі - кут повороту круга 1 відносно осі, що перпендикулярна осям обертання деталі й інструмента, і проходить через центр профілю радіуса ρ¶. 5 40521 Радіус-вектор інструмента можна представити сферичним модулем, що подібний до аналогічного модуля деталі, але зі своїми параметрами r i = S iq × y ×j ×y i i i n Siq ×R i i × ji × r i ×e 4 = M6 (qi ) × M2 (Ri ) × M4 (ji ) × M2 (r i ) × , Siqi ×Ri ×ji ×ri де: r i - радіус-вектор поверхні круга; - сферичний модуль, що являє собою матрицю переходу від початкової точки в систему координат інструмента; θi - кут повороту навколо осі OіZі обертання інструмента; Ri - відстань від центра профілю інструмента до його осі обертання; φi кут повороту навколо осі OіXі; ρi - радіус профілю кола. Радіус-вектор випуклої торової поверхні, яка утворюється після обробки таким інструментом, можна представити через два сферичних модулі й радіус-вектор інструмента: r ¶i = S ф ×y × So × r i q y ¶ i = M6 (q¶ ) × M2 (yc + a × q + t 0 ) ) - модуль де: формоутворення деталі; θ¶ - кут повороту системи координат інструмента відносно осі обертання деталі; у ус+а·θ+t0 - поточна координата між осьової від= стані інструмента й деталі; а·θ=δ - припуск, що знімається; θ -сумарний кут обертання при знятті припуску; t0 - поперечне переміщення t круга, обуt a= 2p мовлене зсувами εу і εz припуску δ (Фіг. 3); - постійна архімедової спіралі, якою у відносному русі переміщується круг при знятті припуску δ; t величина поперечної подачі круга у напрямку, що Sф ×y q¶ 6 перпендикулярний осі O¶Z¶ обертання деталі, на один її оберт; S o = M5 (± y i ) y i - модуль кутової орієнтації інструмента відносно деталі. При знятті припуску, лінія контакту обертається навколо осі деталі за спіраллю Архімеда. Поточна поверхня заготовки утворюється, у вигляді випуклого тора перемінного профілю, з поточним по координаті обробки радіусом ρзі (Фіг. 3). Вихідний припуск враховує зміщення припуску, тобто dmax = d + e 2 + e 2 y z . Зняття припуску відбувається за еквідистантними кривими. Коли припуск знятий, δ=0, t0=0, і у=у с, лінія контакту, яка обертається навколо осі деталі без поперечного переміщення описує форму обробленої випуклої торової поверхні деталі з радіусом ρ¶. Наприкінці обробки необхідно зробити принаймні один оберт інструмента і деталі без врізання для забезпечення остаточного профілю. Правка інструмента проводиться в нахиленому стані. Кут нахилу повинен відповідати кінцевому значенню кута ψ і в процесі обробки. Для підвищення стійкості інструмента можна здійснювати нахил круга як за годинниковою стрілкою, так і в протилежному напрямку (фіг. 2). В цьому випадку нахил відбувається на кут ψ 'i;, а система координат інструмента буде позначатися О'iХ'iY'iZ'i. Підвищення продуктивності шліфування забезпечується завдяки тому, що обробка здійснюється за один прохід, а зняття припуску відбувається одночасно по всьому профілю випуклої торової поверхні за еквідистантними кривими. 7 Комп’ютерна верстка І.Скворцова 40521 8 Підписне Тираж 28 прим. Міністерство освіти і науки України Державний департамент інтелектуальної власності, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601