Навчальна модель “зірчасті багатогранники лося”

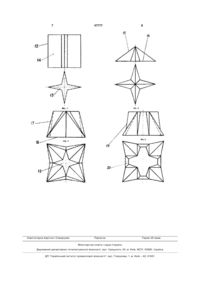
1. Навчальна модель, що містить багатогранники з однаковими трикутними, в тому числі рівносторонніми, рівнобедреними та трапецеїдальними гранями, а також фрагменти зірчастих призм, пірамід, біпірамід, яка відрізняється тим, що в неї входять зірчасті правильні та напівправильні антипризми, призми, піраміди, біпіраміди, призматоїди та біпризматоїди, а також нові двоїсті їм напівправильні багатогранники, причому кожний тип вказаних багатогранників розташований в ряд і кожний член ряду характеризується постійним відношенням числа бічних граней m до числа n з натурального ряду чисел, що означає тут місце в ряду багатогранників, тобто m:n=const, конкретно для зірчастих антипризм це значить, що їх ряд відкриває антипризма (вироджена) з числом бічних граней 4, номером в натуральному ряді чисел 1 і відношенням числа бічних граней до місця в натуральному ряді 4:1=4, далі йде новий 8-гранник (по бічних гранях) з основами у вигляді ромба і відношенням 8:2=4, далі йде новий багатогранник, що має дванадцять бічних граней, у якого основи правильні зірчасті трикутники і відношення 12:3=4, далі алгоритм повторюється до нескінченності, новою напівправильною зірчастою антипризмою є також антипризма, що двоїста по бічних гранях зірчастій 8-гранній антипризмі, що має прямокутні, але не квадратні основи, повернуті на 90°, та бічні грані - чотири однакові трапеції. 2. Навчальна модель за п. 1, яка відрізняється тим, що її ряд відкриває призма (вироджена) з двома гранями і відношенням числа бічних граней до першого числа натурального ряду чисел 2:1=2, далі йде призма з числом бічних граней 4, з основами у вигляді ромба і відношенням 4:2=2, далі йде зірчаста призма з числом бічних граней 6, з основами у вигляді правильних зірчастих трикутників і відношенням 6:3=2, далі йде 8-гранна зірча 2 (19) 1 3 Корисна модель належить до навчальних моделей і призначена для застосування в навчальному процесі при вивченні геометрії, особливо нарисної. Упоминання в назві прізвища автора є даниною традиції, коли геометричні тіла супроводжуються прізвищами авторів (тіла Платона, Архімеда, Пуансо, Кеплера, Федорова, Серпинського, Каталана тощо). Геометрія найкраще розвиває просторову уяву, привчаючи молодь образно мислити, створюючи передумови зображувальних форм життя, що є потужним фактором творчого підходу в багатьох галузях знань, ефективного вирішення нестандартних прикладних задач науки та техніки. Підвищенню ефективності навчання геометрії та графічних дисциплін сприяє застосування навчальних моделей. Ці навчальні моделі часто є фізичними конструкціями, як правило складними та дорогими, що стримує їх широке розповсюдження. Аналогами заявленій моделі по вирішенню навчальних задач є наступні винаходи: авт. свід. СРСР 1656575, кл. G 09 В 23/04, Учебная модель для демонстрации сечения геометрического тела, 1991, Бюл. № 22; а.с. № 1 107152, кл. G 09 В 23/04, Учебный прибор по черчению Усманова, 1984, Бюл. № 29; а.с. № 1339621, кл. G 09 В 23/04, Учебная модель по геометрическому черчению, 1987, Бюл. № 35. Багатогранники складають окремий ефективний навчально-прикладний напрям. Найбільш повний їх опис див. в джерелах: Веннинджер М. Модели многогранников. Пер. с англ., М., "Мир", 1974; Энциклопедия элементарной математики. Книга 4. Геометрия. М.: Физматгиз, 1963 [1] ; Большая Советская Энциклопедия, т. 16, М., 1974, с. 364-366. Застосовуються багатогранники також в будівництві, архітектурі, ювелірній справі. Найближчим аналогом заявленій корисній моделі є багатогранники, описані в вищезазначеній книзі[1] та патенті України № 38968 "Навчальна модель багатогранників(тіла Лося)", Бюл. № 2, 2009. Вивчення вказаних джерел та інших, які не приведені з метою компактності опису, свідчить, що заявлена навчальна модель багатогранників є новою. Ефективність навчального процесу зросте, якщо в вивчення відомих багатогранників ввести раніше невідомі багатогранники, об'єднані в певний ряд алгоритмом у вигляді відповідного математичного виразу. Порівняльний розгляд найближчого аналога та інших джерел показує, що запропонована навчальна модель має наступні особливості: 1. Запропоновані нові зірчасті багатогранники та їх ряди, а саме: антипризми, призми, піраміди, біпіраміди, призматоїди, біпризматоїди, а також нові двоїсті їм напівправильні багатогранники. Зірчасті антипризми, зірчасті призматоїди, біпризматоїди та двоїсті їм багатогранники є новими багатогранниками. Зірчасті призми, зірчасті піраміди та зірчасті біпіраміди відомі фрагментарно, але знайдення їх розташування в безкінечні ряди, побудовані по єдиному алгоритму, є новим фактом в математиці. 47777 4 Ясність алгоритму полегшує вивчення молоддю нових багатогранників. 2. Загальний алгоритм базується на винайденій властивості зірчастих та інших багатогранників, згідно якій відношення числа бокових граней m до місця (номера) багатогранника в натуральному ряді чисел п становить постійну парну величину, яка не змінюється при нескінченному продовжені ряду, тобто: m:n=const ∞. 3. Конкретно по вищевказаним багатогранникам побудова рядів має наступні особливості: для зірчастих антипризм ряд відкриває антипризма(вироджена) з числом бічних граней 4, номером в натуральному ряді чисел 1 і відношенням числа бічних граней до місця в натуральному ряді чисел 4:1=4, другим членом ряду є 8-гранник (по бічним граням) з ромбічними основами і відношенням числа бічних граней до подальшого числа натурального ряду чисел 8:2=4, далі йде новий багатогранник з дванадцятьма бічними гранями, який має основами правильні зірчасті трикутники, а відношення числа бічних граней до наступного числа з натурального ряду 12:3=4, далі йде нова антипризма, що має 16 однакових трикутних бічних граней, основи -правильні зірчасті чотирьохкутники, відношення числа бічних граней до наступного числа з натурального ряду 16:4=4, далі алгоритм повторюється до нескінченності; новою напівправильною зірчастою антипризмою є також антипризма, що двоїста по бічним граням зірчастій 8-гранній антипризмі, маюча прямокутні, але не квадратні, основи, повернуті між собою на 90°, та бічні грані чотири однакові трапеції; новий ряд зірчастих призм відкриває призма (вироджена) з двома гранями і відношенням числа бічних граней до першого числа натурального ряду чисел 2:1=2; далі йде призма з числом бічних граней 4, з основами у вигляді ромба і відношенням 4:2=2; далі йде зірчаста призма з числом бічних граней 6, з основами у вигляді правильних зірчастих трикутників і відношенням 6:3=2; далі йде 8-гранна зірчаста призма з основами у вигляді правильних зірчастих чотирьохкутників та відношенням 8:4=2; далі алгоритм повторюється до нескінченності; для зірчастих пірамід їх ряд відкриває піраміда (вироджена), яка має дві бічні грані, перший номер з натурального ряду чисел і відношення 2:1=2; далі йде чотирьохгранна піраміда з ромбічною основою, номером 2 і відношенням 4:2=2; далі йде 6-гранна піраміда, основа якої - правильний зірчастий трикутник, відношення 6:3=2; далі йде 8-гранна піраміда з основою -правильним зірчастим чотирьохкутником і відношенням 8:4=2; далі алгоритм повторюється до нескінченності з сталою часткою відношення числа бічних граней m до номера з натурального ряду n m:n=const=2 ∞; в зірчастих правильних біпірамідах алгоритм повторюється і є також нескінченним, причому стала частка m:n=4=const ∞; в основі зірчастих призматоїдів та біпризматоїдів, як нових багатогранників, лежать зірчасті правильні багатокутники або інші багатокутники симетричної форми, бічними гранями є трикутники та/або трапеції, причому при тільки трикутних біч 5 них гранях призматоїди та біпризматоїди розташовані в ряди по алгоритму: для призматоїдів з відношенням числа бічних граней m до місця призматоїда в натуральному ряді чисел п m:n=4=const ∞; для біпризматоїдів аналогічно m:n=8=const ∞; першим членом ряду призматоїдів є призматоїд (вироджений) з чотирма бічними гранями і m:n=4:1=4, другим членом є 8-гранник (по бічним граням), з основами - ромбами і відношенням m:n=8:2=4, далі йде 12-гранник, з основами у формі зірчастих правильних трикутників і відношенням m:n=12:3=4, і т.д. до нескінченності; для біпризматоїдів алгоритм повторюється, але з здвоєнням числа бічних граней і частки: const=m:n=8=8:1=16:2=24:3=32:4 ∞. Пояснення потребує термін відносно багатогранників "вироджені". Мається на увазі, що у багатогранників, відкриваючих ряд, для коректної побудови ряду доцільно, щоб з першого члену ряду витримувався заданий алгоритм. Тому ряд відкривають багатогранники, у яких вироджена основа в відрізок прямої лінії. Наприклад, у призматоїдів перший член ряду має основами два відрізки прямої лінії, які розташовані в паралельних площинах під кутом 90° між собою, причому довжина їх різна. Для компактності опису і графічних зображень поглиблені пояснення не приведені. Вказана графічна і аналітична новизна заявлених багатогранників та їх рядів має високий навчальний ефект, сприяючи розвитку в молоді інтересу і впевненості, що активна дослідницька діяльність обов'язково приведе до успіху. Запропонованими моделями показано, як можливо навчати: замість вартісних технічних засобів - легкодоступними графічно і аналітично новими геометричними об'єктами. Заявлені багатогранники в значно скороченому, для компактності опису, об’ємі зображені на відповідних ортогональних проекціях фігур з поз 47777 6 наченням фігур і елементів фігур цифрами: на фіг. 1 показані дві ортогональні проекції нової напівправильної зірчастої 8-гранної (по бічним граням) антипризми 1 з ромбічними основами 2, з трикутними рівнобедреними бічними гранями 3, двоїстим антипризмі 1 багатогранником 4, який складається з двох напівправильних пірамід 5 і напівправильної антипризми 6, що має дві прямокутні, але не квадратні, основи 7, повернуті між собою на 90°, та чотири однакові трапецеїдальні бічні грані 8; на фіг. 2 зображені три ортогональні проекції нової напівправильної зірчастої 12-гранної (по бічним граням) антипризми 9, у якої основами є правильні зірчасті трикутники 10, а бічними гранями рівнобедрені трикутники 11, для полегшення сприйняття двоїстий багатогранник не показаний; на фіг. 3 зображені дві ортогональні проекції 8гранної зірчастої призми 12 з основами 13 у формі правильних зірчастих чотирьохкутників і бічними прямокутними гранями 14, двоїстий багатокутник не показаний; на фіг. 4 зображена в двох ортогональних проекціях 8-гранна правильна зірчаста піраміда 15 з основою у формі правильного зірчастого чотирьохкутника 16; на фіг. 5 приведені дві ортогональні проекції нового зірчастого напівправильного 16-гранного (по бічним граням) призматоїда 17, у якого основами є правильні зірчасті чотирьохкутники 18; на фіг. 6 показані дві ортогональні проекції нового призматоїда 19, до якого введені трапецеїдальні бічні грані 20. Прийоми виготовлення моделей багатогранників широко відомі та наведені також в вищезазначеній книзі Венинджера М. Модели многогранников. Побудовча уніфікованість і різноплановість даних нових багатогранників та їх рядів відкриває шляхи для прикладних застосувань. 7 Комп’ютерна верстка І.Скворцова 47777 8 Підписне Тираж 26 прим. Міністерство освіти і науки України Державний департамент інтелектуальної власності, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601