Безплатформна інерціальна навігаційна система

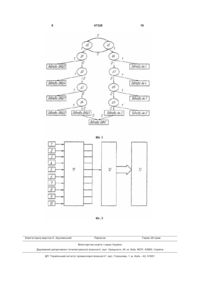
Безплатформна інерціальна навігаційна система, що складається з трьох датчиків кутових швидкостей та трьох акселерометрів, яка відрізняється тим, що в неї додатково введені два датчики кутової швидкості, чутливі осі перших двох датчиків кутових швидкостей співпадають з двома 3 ня з невідомим входом, то єдиний шлях забезпечення виконання критерію структурного діагностування є введення структурної надмірності. Але, введення надмірної кількості датчиків приводить до збільшення маси, габаритів й енергоспоживання БІНС. Подібне обмеження визначає актуальність завдання проектування БІНС БПЛА з мінімальною структурною надмірністю, що дозволяє забезпечувати структурну діагностику БІНС із глибиною до виду відмови. Суть корисної моделі пояснюється кресленнями, де на фіг. 1 показаний варіант розташування осей БІНС із мінімальною структурною надмірністю, на фіг. 2 представлений фрагмент дихотомічного дерева визначення місця відмови в БІНС БПЛА, на фіг. 3 - структурна схема БІНС БПЛА. Запропонований варіант БІНС із структурною надмірністю складається із п'яти датчиків кутової швидкості 1, 2, 3, 4, 5 та п'яти акселерометрів 6, 7, 8, 9, 10, які послідовно підключені через аналогоцифровий перетворювач 11, блок діагностування 12 до блоку формування кутових швидкостей та уявленого прискорення 13. Безплатформна інерціальна навігаційна система працює таким чином. На виході датчиків БІНС БПЛА формується сигнал у вигляді напруги постійного струму. На підставі цього введемо наступні позначення: U1, U2, U3, U4, U5, U6, U7, U8, U9, U10 - значення напруг на виходах датчиків 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 відповідно в к-й момент часу. З огляду на розташування ЧЕ (Фіг. 1) маємо наступні рівняння для датчика кутової швидкості та акселерометра: ì 1 3 wy (t ) + 0wz (t ); ïU1(t ) = wx (t ) + 2 2 ï U2 (t ) = 0wx (t ) + 1wy (t ) + 0wz (t ); ï ïU (t ) = 0w (t ) + 0w (t ) + 1w (t ); ï 3 x y z ; (1) í 1 1 1 ïU (t ) = wx (t ) wy (t ) + wz (t ); ï 4 3 3 3 ï 1 1 1 ïU5 (t ) = wx (t ) + wy (t ) wz (t ); ï 3 3 3 î ì 1 3 a y (t ) + 0a z (t ); ï U6 (t ) = a x (t ) + 2 2 ï ï U7 (t ) = 0a x (t ) + 1a y (t ) + 0a z (t ); ï U (t ) = 0a (t ) + 0a (t ) + 1a (t ); ï 8 x y z ; (2) í 1 1 1 ï U (t ) = a x (t ) a y (t ) + a z (t ); ï 9 3 3 3 ï 1 1 1 ïU10 (t ) = a x (t ) + a y (t ) a z (t ); ï 3 3 3 î де wx(t), wy(t), wz(t), ax(t), ay(t), az(t) - проекції кутової швидкості обертання та уявленого прискорення на осі зв'язаної системи координат. Виходячи з того, що праві частини рівнянь (1) та (2) однакові дослідимо тільки систему рівнянь (1). Тому висновки, які будуть зроблені для (1) будуть слушні для (2). Перепишемо в вигляді матричного добутку (1): 47328 4 é 1 ê é U1(t )ù ê 2 ú ê 0 ê êU2 (t )ú ê êU3 (t )ú = ê 0 ú ê 1 ê êU4 (t )ú ê 3 êU (t )ú ê 1 ë 5 û ê ê 3 ë Позначимо: ù 0 ú ú 0 ú éw ù x 1 ú êw ú (3) úê y ú 1 ú êw ú 3 úë z û 1 ú ú 3ú û 3 2 1 0 1 3 1 3 é 1 ù 3 0 ú ê 2 ê 2 ú 1 0 ú ê 0 ê 0 1 ú. (4) K1 = ê 0 1 1 1 ú ê ú ê 3 3 3 ú ê 1 1 1 ú ê ú ê 3 3 3ú ë û Дослідимо дану матрицю по критерію повного діагностування. З (4) видно, що всі рядки матриці К лінійно незалежні, тобто потрібно перевірити другу умову для всіх симетричних матриць А (3х3) з матриці К. Маємо C3 = 5! = 10 матриць Аі, і=1..10. 5 3!2! Розглянемо ці матриці: A1 = (U1, U2, U3 ); A 6 = (U3, U4 , U5 ); A 2 = (U1, U2 , U4 ); A 7 = (U1, U3 , U4 ); A 3 = (U1, U2, U5 ); A 8 = (U1, U3 , U5 ); (5) A 4 = (U2 , U3 , U4 ); A 5 = (U2 , U3 , U5 ); A 9 = (U1, U4, U5 ); A10 = (U2, U4 , U5 ). Розрахуємо визначник кожної матриці: det (A1) = 0.5; det (A 6 ) = 0.6667; det (A 2 ) = 0.2887; det (A 7 ) = 0.7887; det (A 3 ) = -0.2887; det (A 8 ) = 0.2113; (6) det (A 4 ) = 0.5774; det (A 9 ) = 0.5774; det (A 5 ) = 0.2887; det (A10 ) = 0.6667. З (6) видно, що всі визначники матриці не дорівнюють нулю, тобто даний блок може бути повністю діагностований. Для розрахунку запропонованої корисної моделі складемо логічну таблицю для формування предикатів діагностування. Для кожного блоку ми можемо скласти 5 множин рівнянь, причому з кожної множини можна формулювати показники з одного датчика через всі інші з другої множини. Позначимо такі множини: S1 = (U1, U2 , U3 , U4 ); S2 = (U1, U2, U3, U5 ); S3 = (U2, U3, U4 , U5 ); (7) S4 = (U1, U3 , U4, U5 ); S5 = (U1, U2 , U4 , U5 ). Розглянемо множину S1=(U1,U2,U3,U4). Складемо систему рівнянь для ДКШ: 5 47328 6 U4 (t ) = [2U (t) 3 3U2 ( ( ) ) [ ì 1 3 wy (t ) + 0wz (t ); ïU1(t ) = wx (t ) + 2 2 ï U2 (t ) = 0wx (t ) + 1wy (t ) + 0wz (t ); ï (8) í ïU3 (t ) = 0wx (t ) + 0wy (t ) + 1wz (t ); ï 1 1 1 wx (t ) wy (t ) + wz (t ). ïU4 (t ) = 3 3 3 î З системи рівнянь (8) маємо: ( ) 1 або: 1 ] 1 3 U2 (t ) + 1 3 wzU3 (t ); (10) 1 3U4 (t ) + 3 + 1 U2 (t ) - U3 (t ). (11) 2 З (11) можна позначити як оцінне значення по датчику 1, тобто: 1 ~ ~ ~ ~ U1(t ) = 3U4 (t ) + 3 + 1 U2 (t ) - U3 (t ) . (12) 2 Значить якщо всі датчики справні, то: U1(t ) = ] ì wx (t ) = 2U1(t ) - 3U2 ; ï ï wy (t ) = U2 (t ); ï (9) í wz (t ) = U3 (t ); ï 1 1 1 ïU4 (t ) = wx (t ) wy (t ) + wz (t ). ï 3 3 3 î З (9) випливає: ~ ~ 1 ~ ~ ~ ˆ U1(t ) - U1(t ) = U1(t ) 3U4 (t ) + 3 + 1 U2 (t ) - U3 (t ) » 0. (13) 2 Аналогічно ведуться розрахунки для чотирьох Після проведених розрахунків отримаємо: інших множин s2,s3,s4 та s5. ~ ~ 1 ~ ~ ~ ˆ D1 = U1(t ) - U1(t ) = U1(t ) 3U4 (t ) + 3 + 1 U2 (t ) - U3 (t ) » 0. (14) 2 1 ~ ~ ~ ~ ~ ˆ D 2 = U2 (t ) - U2 (t ) = U2 (t ) 3U5 (t ) - 2U1(t ) + U3 (t ) » 0. (15) 1- 3 [ ( [ ] ) ( ] ] ) [ 3 ~ 3 ~ ~ ~ ~ ˆ U5 (t ) - U2 (t ) » 0. (16) U4 (t ) + D3 = U3 (t ) - U3 (t ) = U3 (t ) 2 2 1 ~ ~ ~ ~ ~ ˆ D 4 = U4 (t ) - U4 (t ) = U4 (t ) 4U1(t ) - 2 3U3 (t )- 3 + 3 U5 (t ) » 0 . (17) 3 -1 1 ~ ~ ~ ~ ~ ˆ D 5 = U5 (t ) - U5 (t ) = U5 (t ) 4U1(t ) - 2 3U2 (t ) - 3U4 (t ) » 0 . (18) 3 Розглянемо вплив відмови кожного ДКШ на Якщо відбулася відмова ДКШ.4, то тотожності тотожностях (14)-(18): (14), (16), (17), (18) руйнуються, тобто дорівнюють Якщо відбулася відмова ДКШ.1, то тотожності нулю. (14), (15), (17), (18) руйнуються, тобто дорівнюють Якщо відбулася відмова ДКШ.5, то тотожності нулю. (15), (16), (17), (18) руйнуються, тобто дорівнюють Якщо відбулася відмова ДКШ.2, то тотожності нулю. (14), (15), (16), (18) руйнуються, тобто дорівнюють З проведеного вище аналізу формуємо настунулю. пні предикатні рівняння: Якщо відбулася відмова ДКШ.3, то тотожності (14), (15), (16), (18) руйнуються, тобто дорівнюють нулю. [ ( [ ] ) ] ì1 - нема відмови (19) z0 = S D1 £ d0 & D 2 £ d0 = í î 0 - відмова { } ì1 - відмова в ДКШ.5 (20) z1 = S D1 £ d0 = í î0 - відмова в ДКШ.1або ДКШ.2 або ДКШ.3 або ДКШ.4 { } ì1 - відмова в ДКШ.4 (21) z2 = S D 2 £ d0 = í î0 - відмова в ДКШ.1 або ДКШ.2 або ДКШ.3 ì1- відмова в ДКШ.1 (22) z3 = S D3 £ d0 = í î0 - відмова в ДКШ.2 або ДКШ.3 ì1 - відмова в ДКШ.2 (23) z 4 = S D 4 £ d0 = í î0 - відмова в ДКШ.3 Отримані предикатні рівняння дають змогу стування у формі дихотомічного дерева, що дає змогу перейти до рішення важливого завдання при сформулювати алгоритм для розв'язання першого та другого завдання діагностування - виявлення побудові діагностичного забезпечення - побудові відмов за допомогою предикату z0 та виявлення правил пошуку місця відмов (ППМ) у БІНС БПЛА. місця відмови за допомогою предикатів z1,z2,z3,z4. Рішення цього завдання засновано на одержанні безумовних ППМ. Це дозволяє представити рішення завдань діагно { } { } { } 7 Розроблене діагностичне дерево (див фіг. 2) у рамках сигнально-параметричного підходу дозволяє вирішувати два найбільш важливих завдання діагностування технічного стану БІНС БПЛА установлення факту виявлення відмови в БІНС і визначення місця його виникнення. 47328 8 Таким чином поставлені завдання повністю вирішуються. Корисна модель дозволяє підвищити відмовостійкість БІНС щодо використання в системах орієнтації на малогабаритних літальних апаратах. 9 Комп’ютерна верстка А. Крулевський 47328 Підписне 10 Тираж 28 прим. Міністерство освіти і науки України Державний департамент інтелектуальної власності, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601