Спосіб побудови системи розмірних рядів твердих лікарських форм (тлф) із застосуванням золотого логарифма
Номер патенту: 62296
Опубліковано: 25.08.2011
Формула / Реферат
1. Система розмірних рядів твердих лікарських форм (ТЛФ) побудована із застосуванням золотого логарифма, яка включає розрахунок констант детермінування таким чином, щоб кожна окрема форма ТЛФ усієї Системи містила числові значення констант детермінування, які відрізняються між собою хоч би одним числовим значенням будь-якої із них і щоб усі константи кожної ТЛФ можна було виразити через одну базову незалежну константу з відповідним показником степеня і ця базова константа ![]() чисельно рівна пропорції золотого поділу, а також щоб кожна окрема форма ТЛФ містила кількісне значення фізичної стійкості, яка однозначно визначається через константи детермінування, а розмірні ряди (крім першого) містили ТЛФ, форма яких змінюється від двоопуклого диска діаметром
чисельно рівна пропорції золотого поділу, а також щоб кожна окрема форма ТЛФ містила кількісне значення фізичної стійкості, яка однозначно визначається через константи детермінування, а розмірні ряди (крім першого) містили ТЛФ, форма яких змінюється від двоопуклого диска діаметром ![]() до форми циліндричної гранули діаметром
до форми циліндричної гранули діаметром ![]() ; притому
; притому ![]() , яка відрізняється тим, що розрахунок констант детермінування і вираження їх через пропорцію золотого поділу, кількісне визначення фізичної стійкості кожної ТЛФ Системи і на основі цих розрахунків графічну побудову Системи розмірних рядів ТЛФ, здійснюють шляхом визначення показника степеня
, яка відрізняється тим, що розрахунок констант детермінування і вираження їх через пропорцію золотого поділу, кількісне визначення фізичної стійкості кожної ТЛФ Системи і на основі цих розрахунків графічну побудову Системи розмірних рядів ТЛФ, здійснюють шляхом визначення показника степеня ![]() базової константи детермінування
базової константи детермінування ![]() із застосуванням золотого логарифма
із застосуванням золотого логарифма ![]() для розрахунку числового значення незалежної константи
для розрахунку числового значення незалежної константи ![]() для будь-якого розмірного ряду Системи і ця константа характеризує відносну випуклість бокової поверхні, залежної константи
для будь-якого розмірного ряду Системи і ця константа характеризує відносну випуклість бокової поверхні, залежної константи ![]() , яка характеризує відносну висоту ТЛФ, а також константи
, яка характеризує відносну висоту ТЛФ, а також константи ![]() , яка характеризує відносний діаметр для кожної ТЛФ усієї Системи розмірних рядів за рівняннями:
, яка характеризує відносний діаметр для кожної ТЛФ усієї Системи розмірних рядів за рівняннями:
![]() ;
;
![]() ;
;
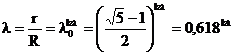 ,
,
![]() -радіус кола перетину бокових поверхонь ТЛФ (радіус диска);
-радіус кола перетину бокових поверхонь ТЛФ (радіус диска);
![]() - радіус кривини бокової поверхні;
- радіус кривини бокової поверхні;
![]() - висота ТЛФ.
- висота ТЛФ.
2. Система за п. 1, яка відрізняється тим, що фізичну стійкість будь-якої ТЛФ Системи розмірних рядів визначають на основі констант детермінування за рівняннями:
фізична стійкість ![]() , (відносна, %) ТЛФ:
, (відносна, %) ТЛФ:
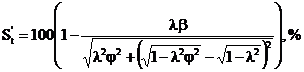
фізична стійкість ![]() (питома, дж/кг) ТЛФ:
(питома, дж/кг) ТЛФ:
![]() .
.
![]() - прискорення сили тяжіння, м/с2;
- прискорення сили тяжіння, м/с2;
![]() - висота максимальна центра ваги ТЛФ над поверхнею підставки.
- висота максимальна центра ваги ТЛФ над поверхнею підставки.
3. Система за п. 1, яка відрізняється тим, що ТЛФ Системи розмірних рядів, задані константами детермінування ![]() , ділимо на категорії "таблетки" або "гранули" за таких співвідношень констант
, ділимо на категорії "таблетки" або "гранули" за таких співвідношень констант ![]() і
і ![]() :
:
якщо ![]() , називаємо таблетки;
, називаємо таблетки;
якщо ![]() , називаємо гранули.
, називаємо гранули.
Текст
1. Система розмірних рядів твердих лікарських форм (ТЛФ) побудована із застосуванням золотого логарифма, яка включає розрахунок констант детермінування таким чином, щоб кожна окрема форма ТЛФ усієї Системи містила числові значення констант детермінування, які відрізняються між собою хоч би одним числовим значенням будь-якої із них і щоб усі константи кожної ТЛФ можна було виразити через одну базову незалежну константу з відповідним показником степеня і ця базова константа 0 чисельно рівна пропорції золотого поділу, а також щоб кожна окрема форма ТЛФ містила кількісне значення фізичної стійкості, яка однозначно визначається через константи детермінування, а розмірні ряди (крім першого) містили ТЛФ, форма яких змінюється від двоопуклого диска діаметром d 0 до форми 3 Корисна модель стосується технології виготовлення твердих лікарських форм (ТЛФ), одержуваних пресуванням, переважно таблеток, сферичних і циліндричних гранул і може бути використана в наукових дослідженнях і промисловому виробництві для оптимізації вибору форми ТЛФ з врахуванням функціональних, технологічних, органолептичних вимог з точки зору технології капсулювання (нанесення плівкового покриття) і призначення цього покриття, а також фізичної стійкості ТЛФ, технічного дизайну. Крім того, корисна модель може бути застосована для однозначного встановлення границі переходу від назви "таблетка" до назви "гранула" в залежності від геометрії ТЛФ заданої константами детермінування. Відомі способи побудови чи вибору розмірних рядів ТЛФ переважно таблеток, на основі рекомендованих співвідношень між їх масою і діаметром, однак у цих рекомендаціях ні форма ТЛФ, ні її геометрія аналітично не взаємопов'язані (не детерміновані). Це ускладнює побудову системи розмірних рядів, а також розрахунок геометрії вибраної форми при зміні маси і (чи) густини ТЛФ [1-5]. Відомі способи оптимізації форми ТЛФ; побудови розмірних рядів ТЛФ із зображенням двох наближених до граничних форм відповідного ряду і "розгортки" ряду для заданого значення незалежної константи детермінування ; визначення фізичної стійкості ТЛФ, однак результати цих досліджень містяться в окремих публікаціях і це ускладнює їх застосування у виробничій практиці і наукових дослідженнях [6-10]. В основу корисної моделі поставлено задачу розробити Систему розмірних рядів ТЛФ одержуваних пресуванням, переважно таблеток, гранул, без обмеження типорозмірів і ступеня випуклості бокових поверхонь, таким чином, щоб кожна окрема форма ТЛФ усієї Системи містила числові значення констант детермінування, які відрізняються між собою хоч би одним числовим значенням будь якої із них і щоб усі константи можна було виразити через одну базову незалежну константу з відповідним показником степеня і ця базова константа 0 чисельно рівна пропорції золотого поділу, а також щоб кожна окрема форма ТЛФ містила числове значення фізичної стійкості, яка однозначно визначається через константи детермінування, а кожен розмірний ряд щоб містив ТЛФ, форма яких змінюється від двоопуклого диска діаметром d0 до форми циліндричної гранули діаметром d0 d d0 ; притому . Вирішення поставленої технічної задачі досягається тим, що, згідно з корисною моделлю, побудову Системи розмірних рядів ТЛФ здійснюють шляхом визначення показника степеня n базової константи детермінування n із застосуванням 0 золотого логарифма lz для розрахунку числового 62296 4 r для будьR якого розмірного ряду Системи і ця константа характеризує відносну випуклість бокової поверхні, H залежної константи f ( ) , яка характериd0 зує відносну висоту ТЛФ, а також константи d f (; ) , яка характеризує відносний діаd0 метр для кожної ТЛФ усієї Системи розмірних рядів за рівняннями: ( n lz ; 1) ( lz log 0 ; 2) lz ( r lz 5 1 0,618lz ; 3) 0 2 R r - радіус кола перетину бокових поверхонь ТЛФ (радіус диска) R - радіус кривини бокової поверхні; H - висота ТЛФ. Примітка: lz - логарифм, основою якого приймаємо базову константу детермінування 0 , чисельно рів значення незалежної константи ну пропорції золотого поділу, називаємо золотий логарифм і позначаємо латинськими буквами (lz) . Задавшись будь-яким числовим значенням незалежної константи детермінування , виражаємо її з допомогою золотого логарифма через базову константу 0 . Аналогічно виражаємо констаd через базову константу 0 . Це d0 дозволяє спростити розрахунок геометрії ТЛФ, форма яких детермінована. Для спрощення розрахунків вихідних даних для побудови Системи розмірних рядів ТЛФ, форма елементів якої змінюється від сферичної до плоско циліндричної, складаємо таблицю золотих логарифмів для ряду чисел від нуля до одиниці. Таблиця значень золотого логарифма для чисел інтервалу (01), включає весь інтервал зміни констант детермінування (0 ;; 1) . У залежності від бажаного кроку зміни констант і вказаний інтервал чисел від нуля до одиниці розбивають на відповідну кількість числових значень цих констант і розраховують для цих чисел відповідні значення золотого логарифма. Для прикладу розраховуємо таблицю (з точністю до третього знака після коми), у якій приводимо обмежену кількість чисел N з інтервалу від нуля до одиниці і відповідні цим числам значення золотого логарифма lzN , з допомогою яких виражаємо довільні значення констант і будьякого розмірного ряду Системи розмірних рядів ТЛФ через базову константу 0 . нту 5 62296 Таблиця N N0 0,090 0,100 0,120 0,146 0,200 0,236 0,245 0,300 0,316 0,382 0,400 0,500 0,600 0,618 0,700 0,750 0,800 0,870 0,900 0,999 N 1 lzN lzN 5,0 4,784 4,405 4,0 3,344 3,0 2,922 2,502 2,394 2,0 1,904 1,440 1,061 1,0 0,741 0,598 0,464 0,289 0,219 0,002 lzN 0 Фізичну стійкість ТЛФ, геометрія яких задана константами детермінування ;; , визначають за рівняннями: відносна стійкість ( S 't , %): S't 1001 2 22 1 22 1 2 6 питома стійкість (St , дж / кг) gh (5) S t S't max , дж / кг . 100 Примітка: Для розрахунку питомої стійкості ТЛФ необхідно, крім констант детермінування ;; , задатися її масою і густиною, тому у Системі розмірних рядів ТЛФ питому стійкість окремих елементів Системи не представлено, оскільки не вказується ні їх маса, ні густина. Це фізичні параметри ТЛФ і вони можуть бути різними для конкретних препаратів. Приклади розрахунку стійкості (відносної) ТЛФ заданих константами детермінування для крайніх і проміжних їх значень. 1. Стійкість сферичних ТЛФ 1 (1-й ряд Системи): 11 , ' 1001 St 0 2 1212 1 1212 1 12 2. Стійкість дуже тонкого двоопуклого диска, константа і відповідно якого прямують до нуля: 19 0,61819 0,0001 0 ; 0 f () 0,00005 0 ; 1 , % (4) 0,0001 0,00005 ' (%) 1001 St 2 2 2 0,0001 12 1 0,0001 12 1 0,0012 0,000000005 1001 100(1 0,00005) 99,995 % 100 % 0,0001 3. Стійкість базового двоопуклого диска, незалежна константа детермінування якого чисельно рівна пропорції золотого поділу: 0 0,618; f ( ) 0,346; 1 0,618 0,346 ' 1001 St 2 0,6182 12 1 0,6182 12 1 0,6182 65 % Тверді лікарські форми, задані константами детермінування ; ; , ділимо на категорії "таблетки" або "гранули" при таких співвідношеннях констант і : d H , називаємо таблетки. d0 d0 d H Якщо , називаємо гранули. d0 d0 Побудова Системи розмірних рядів ТЛФ. Оскільки Система розмірних рядів ТЛФ не накладає обмежень на кількість типорозмірів і крок зміни констант детермінування ; ; , то будуємо для прикладу "малу" Систему розмірних рядів, яка включає шість рядів по п'ять типорозмірів (елементів) ТЛФ у кожному крім першого ряду, оскільки габітус кожного елемента першого ряду однаковий Якщо і має форму кулі діаметр якої залежить тільки від маси і густини ТЛФ. Якщо lz(N0) 0 , то габітус двоопу0 клого диска такого ряду перетворюється в геометричну точку, тому у Системі розмірних рядів ТЛФ "точковий" розмірний ряд не існує. Для проміжних рядів, значення незалежних констант детермінування знаходяться в інтервалі ln(N0) ln(N1) 0 ln 1 , габітус двоопук0 0 лого диска таких рядів має різну ступінь випуклості бокових поверхонь. На кресленні зображено "малу" Систему розмірних рядів ТЛФ. Константи детермінування розмірних рядів ТЛФ і їх стійкість (%) такі: 1-й ряд: 1; S t ,% 0 2-й ряд: 0,463 0,8; 0 f 0,5; 1; 0,87; 0,75; 0,5; 0,245 St 50; 43; 37; 21 6% ; 3-й ряд: 0 0,618; f 0,346; 1; 0,87; 0,75; 0,5; 0,245 S 65; 60; 55; 39;15% t 4-й ряд: 2 0,382; 0 f 0,198; 1; 0,75; 0,5; 0,245; 0,120; St 80; 74; 62; 36;14% 5-й ряд: 3 0,236; 0 f 0,120; 6-й ряд: 5 0,09; 0 f 0,045; 1; 0,5; 0,316; 0,245; 0,120 S 88; 76; 64; 55; 28% t 5 S 95% диск t S 29% градуса t На основі базового диска шостого розмірного ряду можна будувати плоско-циліндричні ТЛФ (таблетки і гранули), змінюючи константу переважно в інтервалі 0,5 5 . Побудована на основі констант детермінуван;; Система розмірних рядів ТЛФ із зазначеня ною фізичною стійкістю кожного елемента Системи зображена на кресленні. Джерела інформації: 1. Державна Фармакопея України 2001р. 2. Фармакопея США 2003 р. 3. Государственная Фармакопея СССР ІХ-ХІ изд. 4. ТИПОВІ ОПИСИ ОСНОВНИХ ФОРМ ТАБЛЕТОК В АНАЛІТИЧНІЙ НОРМА-ТИВНІЙ ДОКУМЕНТАЦІЇ Методичні рекомендації. - К., 2003 р. 5. Носовицкая С.А., Борзунов Е.Е., Сафиулин P.M. Производство таблеток. - М.,1968 г. 6. Устянич А.Є., Устянич Є.П. ПУ №52299 на корисну модель "Спосіб оптимізації форми таблеток". 7. Устянич А.Є., Устянич Є.П. ПУ №54380 на корисну модель "Спосіб побудови розмірних рядів ТЛФ". 8. Устянич О.А., Устянич Є.П. ПУ №53770 на корисну модель "Спосіб визначення стійкості твердих лікарських форм (ТЛФ). 9. Устянич Є. До оптимізації таблеток двоопуклої форми //Фармацевтичний журнал.-1992. - №6. - С. 63-66. 10. Устянич А.Є., Устянич Є.П. Комп'ютеризація капсулювання таблеток двоопуклої форми//Фармацевтичний журнал.-1993. - №1. - С.6972. 9 Комп’ютерна верстка М. Ломалова 62296 Підписне 10 Тираж 23 прим. Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601
ДивитисяДодаткова інформація
Назва патенту англійськоюSystem of size spectrum of solid dosage forms using golden logarithm
Автори англійськоюUstianych Anatolii Yevhenovych, Ustianych Yevhen Petrovych
Назва патенту російськоюСпособ построения системы размерных рядов твердых лекарственных форм (тлф) с применением золотого логарифма
Автори російськоюУстянич Анатолий Евгеньевич, Устянич Евгений Петрович
МПК / Мітки
Мітки: рядів, тлф, форм, логарифма, застосуванням, системі, спосіб, твердих, побудови, лікарських, золотого, розмірних
Код посилання
<a href="https://ua.patents.su/5-62296-sposib-pobudovi-sistemi-rozmirnikh-ryadiv-tverdikh-likarskikh-form-tlf-iz-zastosuvannyam-zolotogo-logarifma.html" target="_blank" rel="follow" title="База патентів України">Спосіб побудови системи розмірних рядів твердих лікарських форм (тлф) із застосуванням золотого логарифма</a>
Попередній патент: Спосіб автоматичного керування процесом зневоднення та гранулювання у псевдозрідженому шарі
Наступний патент: Спосіб підвищення експлуатаційних властивостей підшипників ковзання
Випадковий патент: Захисна охолоджувальна рідина









