Аналоговий суматор-субтрактор напруг

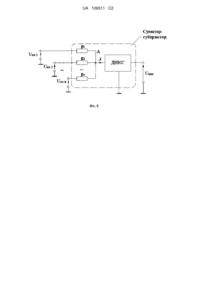
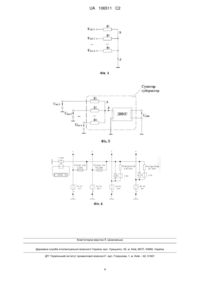
Реферат: Винахід належить до області аналогової обчислювальної техніки та може бути використаний у побудові аналогових і квазіаналогових електричних моделюючих середовищ. Суматорсубстранктор напруг складається з вхідних резисторів, опори яких задають вагові коефіцієнти підсумовування по кожному доданку. Технічним результатом, що досягається даним винаходом, є спрощення схеми суматора-субстрактора. UA 106511 C2 (12) UA 106511 C2 UA 106511 C2 5 10 Передбачуваний винахід належить до області аналогової обчислювальної техніки та може бути використаний у побудові аналогових та квазіаналогових електричних сіткових моделей. Суматор і субтрактор напруг входять до числа базових аналогових схем моделюючих пристроїв. Відомі схеми суматорів та субтракторів складаються з вхідних резисторів та операційного підсилювача (ОП), охопленого зворотним зв'язком. Опори вхідних резисторів разом з опором зворотного зв'язку ОП визначають вагові коефіцієнти підсумовування по кожному доданку, аналогом якого є напруга. Напруга, яка утворюється на виході ОП є аналогом результату підсумовування. У разі субтрактора напруга-аналог від'ємника подається на інвертуючий вхід ОП [1, 296-314; 2, 231-236 та ін.]. Такий суматор виступає як розширювач масштабного інвертуючого підсилювача на ОП і має не менше двох входів (фіг. 1). Для шини А (фіг. 1) можна записати рівняння за методом вузлових напруг:  1 1 1 1   R  R  ...  R  R 2 n зз  1 15 Враховуючи, що  ' 1 1 1 1 Uв х  Uв х1  Uв х2  ...  Uв хn  Uв их  0 ,  R1 R2 Rn R зз  U 'в х  0 при K   , де K - коефіцієнт підсилення ОП, отримаємо: K  1  1 1 Uв их   Uв х1  Uв х2  ...  Uв хn R зз , R  R2 Rn  1  20 40 R3 R2  R3  R 1  зз  R1   R Uв х 2  зз Uв х1 ,  R1  (4) У разі виконання умови R1R3  RззR2 : Uв их  35 (3) тобто вихідний сигнал визначається сумою вхідних сигналів із урахуванням вагових коефіцієнтів у відповідності із правилом підсумовування. Схема, яка формує різницю двох сигналів (субтрактор) зображено на фіг. 2. В такій схемі напруга на виході визначається за виразом [1, 303]: Uв их  30 (2) Коефіцієнти підсилення по кожному із входів визначаються опорами резисторів R1,R2 ,..., Rn та опором зворотного зв'язку Rзз . Відношення K1  Rзз / R1 , K 2  Rзз / R2 ,…, K n  Rзз / Rn , що виступають як коефіцієнти підсилення по кожному із вхідних каналів, називають також ваговими коефіцієнтами. Враховуючи це, отриманий вираз можна записати так: Uв их  (К1Uв х1  К 2Uв х2  ...  К nUв хn ), 25 (1)   R зз Uв х2  Uв х1 , R1 (5) Отже, якщо до суми входять також від'ємні складові, то необхідно використовувати операційний підсилювач із інвертуючим входом. Крім того, вибір Rзз виявляється компромісним і залежить від конкретних умов [2, 231-236]. Приймаємо за прототип схему, представлену на фіг. 1. Як недоліки прототипу відзначимо необхідність використання операційного підсилювача з інвертуючим входом і з колом зворотного зв'язку, параметр якого визначає коефіцієнт підсумовування кожного доданку. Задачею винаходу є усунення недоліків прототипу. Поставлена задача досягається тим, що схема суматора-субтрактора включає вхідні резистори, які мають додатну при додаванні і від'ємну [3] при відніманні провідність, приєднані до підсумовуючої шини з'єднаною через керуючі виводи джерела напруги керованого струмом із спільною точкою схеми (заземлення). 1 UA 106511 C2 5 Електричні аналоги доданків, як струми утворені напругами на вхідних резисторах, подаються на підсумовуючу шину, на якій, згідно першого закону Кірхгофа, утворюється сумарний струм. Напруга керованого джерела напруги, яка визначається сумарним струмом підсумовуючій шині, є результатом додавання. При цьому відпадає необхідність у використанні ОП із колом зворотного зв'язку. Зіставимо схемі фіг. 1 іншу схему, представлену на фіг. 3. Вона складається із підсумовуючої шини (А) і провідностей g1, g2,..., gi ,..., gn . Ця схема описується рівнянням: (g1  g2  ...  gn )Uв х'g1Uв х1  g2Uв х2  ...  gnUв хn  0 , 10 Тут Якщо заземлити шину А, то Uв х'  0 і в результаті отримуємо схему, представлену на фіг. 4. J  g1Uв х1  g2Uв х2  ...  gnUв хn , 15 (7) Застосувавши в схемі фіг. 4 джерело напруги, кероване струмом (ДНКС) із коефіцієнтом керування K дж  Uв их / Iв х  1 Ом, отримаємо схему передбачуваного винаходу, показану на фіг. 5, у якій Uв их  g1Uв х1  g2Uв х2  ...  gnUв хn , 20 (6) (8) тобто квазіаналогова модель суматора перетворюється у аналогову. Нехай необхідно отримати значення виразу виду: S  a1x1  a2 x 2  ...  ai xi  ...  an xn , (9) Складові цієї суми у схемі фіг. 5 моделюються провідністю gi ~ ai , напругою U i ~ xi і вихідною напругою Uв их ~ S . Отже має місце пряма аналогія. 25 30 35 40 45 Відзначимо, що схема фіг. 5 не має недоліків прототипу. Провідності gi ,... gn і відповідні їм опори можуть приймати як додатні, так і від'ємні значення завдяки використанню резисторів із регульованими додатними і від'ємними статичними параметрами (ККr) [3], що відповідає додатним і від'ємним значенням коефіцієнтів ai в (9). Все це значно спрощує використання аналогового суматора-субтрактора на відміну від суматора на операційному підсилювачі, охопленого зворотним зв'язком, із інвертуючими входами. В залежності від знаку gi схема може відтворювати додавання і віднімання. На фіг. 6 представлений приклад реалізації зазначеного суматора-субтрактора в середовищі Electronics Workbench [4]. Показано знаходження значення виразу при x1  6, x 2  10, x 3  15, x 4  4 . Результат отримано як значення напруги x1  2x 2  4x 3  5x 4 U  54 B. Враховуючи, що у середовищі Electronics Workbench функціонують віртуальні струми, напруги та елементи електричних кіл, етап масштабування при побудові електричної моделі відпадає. Опори резисторів прямо визначаються через провідності, які чисельно дорівнюють коефіцієнтам заданого виразу, а значення е.р.с. - через значення x1, x 2 , x 3 , x 4 . Джерела інформації: 1. Уве Наундорф. Аналоговая электроника. Основы, расчет, моделирование. - М.: Техносфера, 2008.- 472 с. 2. А.Дж.Пейтон, В.Волш. Аналоговая электроника на операционных усилителях. - М.: БИНОМ, 1994.- 352 с. 3. Патент на корисну модель № 59292, Україна, МПК G06G 7/100, Карандаков Г.В., Кривенко В.І., від 10.05.2011, Бюл. № 9, 2011 р. 4. Электротехника и электроника в экспериментах и упражнениях: Практикум на Electronics Workbench: в 2 т. / ред. Д.И.Панфилов. - М.: Изд-во "Додека", 1999. 2 UA 106511 C2 ФОРМУЛА ВИНАХОДУ 5 Аналоговий суматор-субтрактор напруг складається із вхідних резисторів, опори яких задають вагові коефіцієнти підсумовування по кожному доданку, та операційного підсилювача з інвертуючим входом та колом зворотного зв’язку, який відрізняється тим, що вхідні резистори, які мають додатну провідність при додаванні та від’ємну провідність при відніманні, приєднані до підсумовуючої шини, яка з’єднана, через керуючі виводи джерела напруги керованого струмом, із спільною точкою заземлення. 3 UA 106511 C2 Комп’ютерна верстка Л. Ціхановська Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601 4