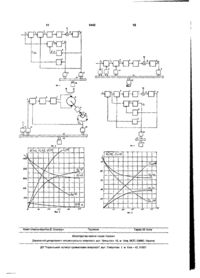
Спосіб ідентифікації параметрів координатних збурень автоматичних систем
Формула / Реферат
Спосіб ідентифікації параметрів координатних збурень автоматичних систем шляхом виділення з рівнянь руху регульованої координати складової, що пропорційна сигналу завдання, який відрізняється тим, що вимірюють регульовану координату, отримане значення масштабують і порівнюють з сигналом завдання і подають на вхід моделі, сигнал на виході моделі масштабують та алгебраїчно сумують з сигналом завдання і формують сигнал на вході автоматичної системи регулювання, вимірюють сигнали ![]() на виході моделі, визначають значення
на виході моделі, визначають значення ![]() нелінійних складових діючих збурень відповідно рівнянням
нелінійних складових діючих збурень відповідно рівнянням
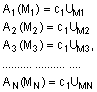
де:
![]() - коефіцієнт пропорційності,
- коефіцієнт пропорційності,
далі визначають значення діючих збурень ![]() відповідно рівнянням
відповідно рівнянням
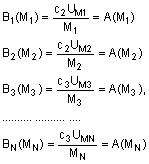
де
![]()
![]() - коефіцієнт пропорційності,
- коефіцієнт пропорційності,
далі здійснюють перше наближення полінома ![]() для
для ![]()
![]()
де
![]() - параметр полінома за умови
- параметр полінома за умови ![]() звідки
звідки
![]()
після цього визначають точність наближення полінома
![]()
здійсненням наступних обчислень
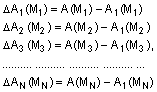
при ![]() продовжують наближення полінома для
продовжують наближення полінома для ![]()
![]()
звідки знаходять параметри ![]() полінома
полінома
![]()
і знову проводять оцінку наближення, процедуру наближення здійснюють, поки буде виконуватися умова ![]()
Текст
Спосіб ідентифікації параметрів координатних збурень автоматичних систем шляхом виділення з рівнянь руху регульованої координати складової, що пропорційна сигналу завдання, який відрізняється тим, що вимірюють регульовану координату, отримане значення масштабують і порівнюють з сигналом завдання і подають на вхід моделі, сигнал на виході моделі масштабують та алгебраїчно сумують з сигналом завдання і формують сигнал на вході автоматичної системи регулювання, вимірюють сигнали UMI,UM2.UM3>-->UMN виході моделі, визначають А-|(М-|),А2(М2),Аз(Мз),..., AN(M[SJ) на значення ДЄ В(М) = А(М). м ' С2 - коефіцієнт пропорційності, далі здійснюють перше наближення А(М) для N - 2 полінома де а-| - параметр полінома за умови a-j =B(0), звідки після цього визначають точність наближення полінома здійсненням наступних обчислень нелінійних складових діючих збурень відповідно рівнянням = А(Мз)-А 1 (М 3 ), м(^|)(м,(м) Де: сі - коефіцієнт пропорційності, далі визначають значення діючих М-|,М2,Мз.—,Mfs| відповідно рівнянням при AA,(Mj)*0 продовжують наближення полінома для N = З CM а-] + а2Мі + азМ1^ (О о збурень звідки знаходять параметри а2,аз полінома В 2 (М 2 ) = C2UM2 М2 C 3 U M N = A(M ) N MN А 2 (М) = а-]М + а 2 М 2 +а 3 М 3 і знову проводять оцінку наближення, процедуру наближення здійснюють, поки буде виконуватися умова AJM(MN) = СП 6442 Корисна модель відноситься до галузі автоматичного регулювання і може бути використана для ідентифікації параметрів координатних збурень, які мають нелінійну та нестаціонарну залежність між регульованою координатою і збуренням. Відомий спосіб Ідентифікації координатних збурень шляхом вимірювання регульованої координати і вирахування пропорційного збурення [1]. Недолік відомого способу ідентифікації полягає в обмежених функціональних можливостях, які визначаються умовами стаціонарності прикладеного до об'єкту керування збурюючого діяння. Проте, більшість збурюючих діянь, які прикладаються до координат регульованих об'єктів, за своєю природою являються як нелінійними так і нестаціонарними. Відомий спосіб ідентифікації з використанням моделі, який дозволяє використати його в умовах нестаціонарності параметрів збурень [2]. Недолік відомого способу ідентифікації полягає в низькій точності ідентифікації визначення параметрів функції збурення при зміні вигляду цього збурення. Відомий спосіб ідентифікації координатних збурень автоматичних систем шляхом виділення з рівнянь руху регульованої координати складової, що пропорційна сигналу завдання [3], прототип. Недолік відомого способу полягає в тому, що його неможливо використовувати в природних умовах експлуатації автоматичної' системи, так як для його здійснення необхідно використовувати давач збурюючих діянь. Крім того, спосіб обмежено використанням лінійних об'єктів. Задачею пропонованого способу є підвищення точності визначення параметрів координатних збурень автоматичних систем шляхом виділення корисного сигналу від адитивних та мультиплікативних перешкод. Поставлена задача вирішується тим, що в способі ідентифікації параметрів збурень автоматичних систем шляхом використання моделі, новим являється те, що вимірюють сигнал пропорційний регульованій координаті, отримані значення масштабують і порівнюють з сигналом завдання; отримане значення подають на вхід моделі, сигнал на виході моделі масштабують та алгебраїчно сумують з сигналом завдання і формують сигнал на вході автоматичної системи регулювання. Далі вимірюють сигнали UMI (MI ), UM2(M2), иМз(Мз),..., UMN(MN) на виході моделі, визначають значення Ат(Мі), А 2 (М 2 ), А3(М3),..., AN(MN) нелінійних складових діючих збурень відповідно рівнянням де Сі - коефіцієнт пропорційності. Потім визначають значення діючих збурень Мі, М 2 , М3,.., MN ВІДПОВІДНО рівнянням М2 м3 щ де Bj(Mj) = АЖ) Мі Сг - коефіцієнт пропорційності, далі здійснюють перше наближення полінома А(М) аі+а 2 М 2 =Ві(Мі), де аі - значення першого параметра при М=0, тоді 2 М-, відповідно, поліном збурень має вид А,(М)=аіМ+а 2 М 2 . Далі, виконують оцінку точності отриманих значень відповідно рівнянням ДА 2 (М 2 ) - А(М 2 ) = А(М 3 )-А 1 (Мз) при ДАі(М() > ДАз(Мі), де ДАз(М,) задане значення помилки, продовжують обчислення. Тоді друге наближення має вид г або а2М2+азМ22=В2(М2)-аі, відкіля знаходять значення параметрів аг і аз полінома А(М) А2(М)=аі М+а 2 М 2 +а 3 М 3 , після цього виконують перевірку точності відповідно з рівнянням Д 2 1 (М 1 ) = А(М 1 )-А 2 1 (М 1 ) Д 2 2 ( М 2 ) - А(М 2 ) - А 2 2 ( М 2 ) Д23(М3) = А{М3)-А23(М3) , Процедура наближення повторюється до тих пір поки А,(Мі)=А(М). На Фіг.1 подана структурна схема системи ідентифікації параметрів координатних збурень слідкуючої системи. На ФІГ.2 подана структурна схема системи ідентифікації параметрів координатних збурень слідкуючої системи з мікропроцесором (МП). Па Фіг.З подана принципова схема системи ідентифікації параметрів координатних збурень. На Фіг.4 подана принципова схема здійснення способу з використанням мікропроцесора. 6442 На Фіг.5 і 6 представлені характеристики процесів ідентифікації до розрахункових прикладів. Система для здійснення запропонованого способу (Фіг. 1) утримує перший, другий і третій 1, 2, З суматори, підсилювач 4, об'єкт регулювання 5, вимірювач регульованої координати 6, модель 7, масштабні перетворювачі 8 і 9, блоки вводу аналогових сигналів - аналого-цифрові перетворювачі (АЦП) 10 і 11, інтерфейс 12, процесор 13. Блоки 26-2 утворюють контур слідкуючої системи, а блоки 1-3, 7, 8, 9 та мікропроцесор утворюють систему системи ідентифікації" параметрів координатних збурень. Спосіб здійснюється наступним чином Рівняння статичної характеристики системи автоматичного регулювання з нелінійною залежністю між регульованою координатою та діючим збуренням має вид 0=Ке-А(М), (1) де є, 0, М - відповідно, сигнал керування, регульована координата і координатне збурення; К- коефіцієнт передачі по керуючому сигналу; А(М} - поліном N-oro ступеня, який визначається рівнянням A(M)=aiM+a2M2+a3M3+...+aNMN, (2) аі, аг, аа.-.aN - параметри координатних збурень, які визначаються із системи рівнянь 6 Далі, сигнал UM масштабується, алгебраїчно підсумовується з сигналом завдання єз і формується регульована координата 0 відповідно рівнянню де рм - коефіцієнт масштабного перетворювача 9. Тоді отримаємо -А(М), (10) і.(11) На основі (1)-(9) одержують систему 2-х координатно пов'язаних рівнянь '. (12) і,(13) Систему рівнянь (12) (13) можна подати в матричній формі -кмРЇ©] = Г к 1 1 U K 1 MJ L M 3 Гі] Гї LOJ Рішенням системи (14) відносно змінних 0, U 0 , є система 2-х параметрично пов'язаних рівнянь 0=К(1+Кмрм)ез-АЭ(М),(15) 1,(16) і, Кр= 1 (17) за рахунок вибору коефіцієнта р*=1/К рівняння (11)-(12) приводяться до виду (18) + a2M|sj 2 + азМім 3 + • • + а\фЛ^ . = On - О ^ де Мі, М2,..., MN - відомі значення збурень; Оь Ог,..., ON - виміряні значення регульованої координати; Эо=Ке - значения регульованої координати при відсутності зовнішніх збурень. Рівняння (2) може бути подано в наступному вигляді А(М)=В(М)М, (4) де В(М)=а1+а2М+а3М2-к..+амМы"1. (4) Тоді рівняння (1) буде мати наступний вид 0=Э о -В(М)М, (5) Де 00-0 В(М) = м (6) - чутливість статичної характеристики автоматичної системи відносно координатного збурення. Для здійснення пропонованого способу використовується модель з функцією перетворення виду UM=KM£M, (7) де £м, UM - сигнали на вході та на виході моделі; Км - коефіцієнт перетворення моделі. Відповідно пропонованому способу сигнал U 9 пропорційний регульованій координаті 0 масштабується, алгебраїчно підсумовується і сигналом завдання £з і формується сигнал на виході моделі відповідно рівнянню єм=Км(£з-и0{і), (8) де U Q = K Q 0 , К 9 - - коефіцієнт перетворення давача 6, p - коефіцієнт масштабного перетворювача 8. " 1+КмРм А(М). (19) Таким чином, в результаті взаємопов'язаних і ціленаправлених дій, які виконуються над матеріальними об'єктами, одним з яких с автоматична система, а другим - модель, утворені дві структури, які функціонально визначаються рівняннями (15), (16). З рівняння (19) очевидно, що сигнал UM з виходу моделі інваріантний відносно сигналу завдання Єз, І A(M)=CiUM, (20) де - коефіцієнт пропорційності. При цьому, модель функціонально не сприймаюча збурення М, формує сигнал UM, ЯКИЙ утримує всі компоненти цих збурень. Таким чином, рівняння (11), (12) характеризують отримані перетворення як багато зв'язану систему. Враховуючи, що сигнал U 9 на виході перетворювача 6 дорівнює U e =K R 0 рівняння (14), (15) будуть відповідати наступній системі К -® - А ( М ) , (21) З рівняння (22) бачимо, що сигнал з виходу моделі UM інваріантний відносно сигналу єз. Це означає, що якщо сигнал єз крім постійної складової отримує ще сигнал перешкоди, наприклад, 6442 еры), тобто отримує адитивну суміш гармонік, то рівняння (22) інваріантне відносно перешкоди. Далі, в процесі виконання запропонованого способу, вимірюють сигнали UMI, UM2. UM3,..., UMN на виході моделі, визначають значення полінома збурень А(М) 8 При незадовільних результатах продовжують наближення полінома А(М), при N=3 Мі а 2 М 2 + а 3 М г 2 = В 2 (М 2 ) = (ЗО) М2 або + азМ-j2 = A 3 (M) = c 1 U M 3 .(23) .(31) а2М2 Рівняння (31) можуть бути представлені в матричній формі де сі - коефіцієнт пропорційності, далі визначають значення діючих збурень і, Мз,.-., MN, а також відповідних функцій ,(32) ,(33) Лг=(Вг(М2)-а0Мі2-(Ві(Мі)-а1)М22, (34) Д=МіМ 2 2 -М 2 Мі 2 , (35) В 2 (М 2 ) = С2УМ2 М2 а а2=-^І, .(24) м3 &3=~ (36) (37) ТОДІ, ПОЛІНОМ ДІЮЧИХ збурень має де с2 - коефіцієнт пропорційності. В(М)=^М. (25) Далі здійснюється перше наближення полінома А(М), при N=2 де (26) М-) - значення параметра аі = В(0) звідки M-t ^ (27) v іА 1 (М)=а 1 М+а 2 М 2 . (28) Далі проводять оцінку точності першого наближення при ,(29) вид А2(М)=а1М+а,М2+а3М3. (38) Перевірку точності проводять відповідно рівнянням (39) А2(М2) (40) і так далі, поки ANA N (MN)=0. Для доказу здійснення запропонованого способу приведемо розрахунковий приклад. Задамо наступні параметри системи; КИ00, Км=10, К0=О,1, р=0,01, (5м=0,1, Єз=10. Тоді рівняння (15), (16) будуть мати вид Є=1000-0,5А(М) U0=1OO-O,O5A(M). UM=0,05A(M) Поліном (2) має вид А(М)=43,2М-0,89М2+0,0062М3 В(М)=43,2-0,89М+0,0062М2. Характеристики змінювання змінних зведені в таблицю 1 і приведені на Фіг.5. = A(MN)-A1(MN) Таблиця 1 м А(М) В(М) є UM 0 0 43,2 1000 100 0 10 349,2 34,92 825,4 82,54 1,746 Далі, відповідно рівнянню (20), визначають значення діючих збурень 20 557,6 27,88 721,2 72,12 27,88 30 662,4 22,08 668,8 66,88 33,12 50 710,0 14,2 645,0 64,5 35,5 A 5 ( M ) = 2 0 U M S = 2 0 ' 3 5 ,58=710,0 Далі складають рівняння AI(M)=20UMI=20*17,46=349,2 A2(M)=20UU2=20*27,88=557,6 A3(M)=20UM3=20*33,12=662,4 40 700,8 17,57 649,6 64,96 35,04 = 34,92, звідки 6442 B1(M1)=34,92 Mi=10 M2 10 10 -100І_Г8,28ІГаі 20 -400J~[i5,32j|_a2 Тоді M2 звідки В2(Ма)=27,88 Мі=20 То перше наближення припускає лінійність функції В(М) аі+а2М,=34,92 43,2+а2*10=34,92, звідки аг=-0,828. Тоді функція діючих збурень має вид 2 Аі(М)=43,2М-0,828М Перевірка точності наближення дає значення помилки Аі{М1)=432-82,8=349,2 Аі(М2)=864-331,2=532,8. Помилка дорівнює ЛА(М)=3,3%. Наступне друге наближення має вид Ді -3312 + 1532 п п п аі = —і= 0,89 Д -2000 Л2= 2 Д -2000 шукаємий поліном збурень має вид s 2 A1(M)=43,2M-0,89M +0,0062M . Перевірка точності дає наступні результати А 2 (10) = 432 - 89 + 6,2 - 349,2 А 2 (20) = 864 - 356 + 49,6 = 557,6 А 2 (50) - 2160 -2225 + 775 = 710,0 що доводить досягнення поставленої задачі в діапазоні заданих умов. А(М)=50М-0,52М2+0,0075М2 Приклад 2 В(М)=50-0,52М+0,0075М2 Результати розрахунків наведені в таблиці 2 і показані на Фіг.6. Таблиця 2 м Аг(М) В2(М) мвг UM2 0 0 50 1000 100 0 20*22,77 = 45,55 Мі=10 Ві(Мі)=45,55 20 * 42,6 = 4276 М2 М2=20 Вг(М2)=42,6 at*10-a2*100=4,45 а1*20-а2*400=7,4 10 -1001 [4,45 20 -400_|~|_7,4 -1780 + 740 = 0,52 -2000 74-89 = 0,0075 -2000 10 455,5 45,55 772,25 77,25 22,77 20 852 42,6 574 57,4 42,6 ЗО 1234,5 41,15 383 38,3 61,72 40 1648 41,2 176 17,6 82,4 50 2137,5 42,75 130 13,0 106,85 Тоді функція збурення має вид А2(М)=50М-0,52М2+0,0075М3, що доводить здійснення запропонованого способу в умовах параметричних та сигнальних збурень. Джерела інформації: 1. Авторское свидетельство СССР №744473, 1980. 2. Кику А. Г. и др. Адаптивные системы идентификации. К., «Наукова думка», 1975, с.5-23. 3. Авторское свидетельство СССР №873209, 1981. 4. Авторское свидетельство СССР №1327067, 1987. 6442 Комп'ютерна верстка Д Шеверун Підписне 12 Тираж 28 прим Міністерство освіти і науки України Державний департамент інтелектуальної власності, вул Урицького 45, м Київ, МСП, 03680, Україна ДП "Український інститут промислової власності", вул Глазунова 1 м Київ-42, 01601
ДивитисяДодаткова інформація
Назва патенту англійськоюMethod for identifying parameters of perturbation actions in an automatic control system
Назва патенту російськоюСпособ идентификации параметров возмущающих воздействий в системе автоматического регулирования
МПК / Мітки
МПК: G05B 23/02
Мітки: автоматичних, систем, параметрів, ідентифікації, спосіб, збурень, координатних
Код посилання
<a href="https://ua.patents.su/6-6442-sposib-identifikaci-parametriv-koordinatnikh-zburen-avtomatichnikh-sistem.html" target="_blank" rel="follow" title="База патентів України">Спосіб ідентифікації параметрів координатних збурень автоматичних систем</a>
Попередній патент: Модифікатор для алюмінієвих сплавів
Наступний патент: Спосіб одержання стабілізатора накипоутворення та інгібітора корозії сталі на основі нітрилоксіетилдиметилфосфонової кислоти
Випадковий патент: Передатний пристрій механічного приводу