Спосіб налаштування пропорційно-інтегрального регулятора для мехатронних систем
Номер патенту: 75909
Опубліковано: 25.12.2012
Автори: Ромасевич Юрій Олександрович, Ловейкін Вячеслав Сергійович
Формула / Реферат
Спосіб налаштування пропорційно-інтегрального регулятора для мехатронних систем, що мінімізує інтегральний тип критерію якості регулювання, який відрізняється тим, що встановлюють вагові коефіцієнти ![]() та
та ![]() із врахуванням вимог, які ставляться до якості регулювання руху мехатронної системи; надалі задають величини коефіцієнтів підсилення інтегральної та пропорційної складових пропорційно-інтегрального регулятора у відповідності до виразів:
із врахуванням вимог, які ставляться до якості регулювання руху мехатронної системи; надалі задають величини коефіцієнтів підсилення інтегральної та пропорційної складових пропорційно-інтегрального регулятора у відповідності до виразів:
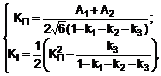
де ![]() та
та ![]() - коефіцієнти підсилення інтегральної та пропорційної складових ПІ-регулятора відповідно;
- коефіцієнти підсилення інтегральної та пропорційної складових ПІ-регулятора відповідно; ![]() - коефіцієнти, які визначаються із виразів
- коефіцієнти, які визначаються із виразів
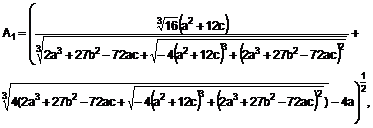
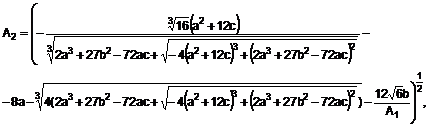
![]() ,
,
![]() ,
,
![]() та
та ![]() - вагові коефіцієнти, які враховують положення, швидкість та величину функції керування рухом мехатронної системи відповідно.
- вагові коефіцієнти, які враховують положення, швидкість та величину функції керування рухом мехатронної системи відповідно.
Текст
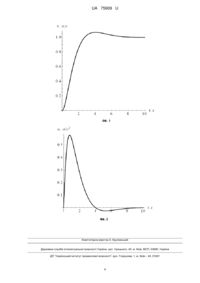
Реферат: Спосіб налаштування пропорційно-інтегрального регулятора для мехатронних систем, що мінімізує інтегральний тип критерію якості регулювання. Встановлюють вагові коефіцієнти k1,k 2 та k 3 із врахуванням вимог, які ставляться до якості регулювання руху мехатронної системи; надалі задають величини коефіцієнтів підсилення інтегральної та пропорційної складових пропорційно-інтегрального регулятора. UA 75909 U (54) СПОСІБ НАЛАШТУВАННЯ ПРОПОРЦІЙНО-ІНТЕГРАЛЬНОГО РЕГУЛЯТОРА ДЛЯ МЕХАТРОННИХ СИСТЕМ UA 75909 U UA 75909 U 5 10 15 20 25 30 35 40 Корисна модель належить до галузі автоматики, зокрема до способів налаштування автоматичних регуляторів, які використовуються для керування рухом мехатронних систем. Пропорційно-інтегральний (ПІ-) регулятор є частинним випадком пропорціональноінтегрально-диференціального регулятора, який детально описаний у технічній літературі (Денисенко В.В. ПИД-регуляторы: принципы построения и модификации // Современные технологии автоматизации. Часть 1. 2006, №4. с. 66-74; Часть 2. 2007, №1. с. 78-88). Одним із способів налаштування коефіцієнтів підсилення пропорційної, інтегральної та диференціальної складових регулятора є спосіб запропонований Зіглером і Нікольсом (John G. Ziegler and Nathaniel В. Nichols, "Optimum Settings for Automatic Controllers", Trans. ASMH, Nov. 1942, pp. 759-768.). Це один із найпоширеніших на практиці способів, він дає не дуже гарні показники регулювання. Одним із способів налаштування коефіцієнтів підсилення регулятора є спосіб запропонований у праці (Chien K.L., Hrones J.A., Reswick J.B. On automatic control of generalized passive systems // Trans. ASME. 1952. Vol. 74. P. 175-185.). Даний спосіб ґрунтується на критерії не більш ніж 20-ти відсоткового перерегулювання. Одним із недоліків вказаного способу є те, що він базується на апроксимації об'єкта регулювання моделлю першого порядку із затримкою. Така апроксимація не завжди вдало відображає реальну динаміку руху об'єкта, що є недоліком даного способу. Широко використовуваним способом налаштування автоматичних регуляторів є ручний спосіб, який ґрунтується на певних правилах (Изерман Р. Цифровые системы управления. - М.: Мир, 1984. - 541 с). Однак такі правила справедливі тільки у околі оптимальних параметрів регулятора, тобто вимагається початкове налаштування регулятора за іншими способами, що є недоліком даного способу. Загальним недоліком описаних способів налаштування регуляторів є те, що керуюча дія (вихідна велична регулятора) може приймати неприпустимо великі значення, тобто приводний механізм, який є виконавчим елементом мехатронної системи, не в змозі реалізувати керуючу дію при відпрацюванні значної уставки або при дії на мехатронну систему значних збурень. У результаті алгоритм регулювання "зривається". Крім того, можна вказати ще один недолік відомих регуляторів: велике значення керуючої величини, пропорційної, наприклад, електромагнітному моменту приводного двигуна, на початку регулювання. Це може викликати удари у кінематичних зачепленнях та вихід з ладу елементів приводу мехатронної системи. Найбільш близьким за технічною суттю та ефектом, що досягається, до запропонованого способу налаштування ПІ-регулятора для мехатронних систем є спосіб визначення коефіцієнтів підсилення складових ПІ-регулятора (Методы классической и современной теории автоматического управления: ученик в 5-ти томах; 2-е изд., перераб. и доп. Т. 4: Теория оптимизации систем автоматического управления / Под ред. К.А. Пупкова и Н.Д. Егупова. - М.: Издательство МГТУ им. Н.Э. Баумана, 2004. - 744 с.). Даний спосіб вибрано за прототип. Згідно із прототипом коефіцієнти підсилення відповідних складових регулятора підбираються таким чином, щоб мінімізувати критерій, що відображає якість процесу регулювання. Критерієм якості регулювання прототипу є інтегральний функціонал: T 2 I ( x1 x 2 u 2 )dt , (1) 2 0 45 де x 1 та x 2 - фазові координати системи (положення та швидкість ланки приведення машини, наприклад вала двигуна); u - функція керування системою; T - тривалість регулювання. Фазові координати та функція керування пов'язані співвідношеннями: x1 x 2 ; (2) x 2 u. Вираз, який описує функцію керування прототипу, що забезпечує асимптотичну стійкість системи регулювання та мінімізує критерій (1) має такий вигляд: 50 u x1 3 x 2 . (3) Прототип та заявлена корисна модель мають спільні ознаки: вони мінімізують інтегральний тип критерію якості регулювання при налаштуванні ПІ-регулятора. Недоліком прототипу є те, що за великих значень фазових координат мехатронної системи початкова величина функції керування може приймати недопустимо великих значень. Це може виникнути у випадках задання великої уставки (розгін мехатронної системи до значної номінальної швидкості) або впливу на рух мехатронної системи значних збурюючих зусиль. У 1 UA 75909 U 5 10 результаті двигун мехатронної системи на початку руху повинен створити великий крутний момент, що може викликати удари у кінематичних зачепленнях приводу. Задачею корисної моделі є зменшити початкову величину функції керування рухом мехатронної системи. Поставлена задача вирішується тим, що коефіцієнти підсилення ПІ-регулятора налаштовуються за виразами, які є складними функціями вагових коефіцієнтів інтегрального критерію якості регулювання. Суть корисної моделі пояснюється рисунками: на Фіг. 1 показано графік зміни швидкості руху мехатронної системи при її розгоні, на Фіг. 2 - графік функції керування рухом мехатронною системою. Графіки побудовані при умовах: уставка швидкості x 2 T x 2 0 1 м/с, значення вагових коефіцієнтів k1 0,5,k 2 k 3 0,2 , тривалість регулювання T 10 секунд. Коефіцієнти підсилення складових ПІ-регулятора налаштовуються таким чином, щоб мінімізувати критерій якості регулювання руху мехатронної системи інтегрального типу: T 2 I (k1x1 k 2 x 2 k 3u 2 (1 k1 k 2 k 3 )u 2 )dt , (4) 2 0 15 20 де k1,k 2 та k 3 - вагові коефіцієнти, які враховують положення, швидкість та величину функції керування рухом мехатронної системи відповідно. Крапка над символом означає диференціювання за часом. Керування, яке забезпечує асимптотичну стійкість руху мехатронної системи, мінімізує критерій (4) та дозволяє встановити початкове керування рівне нулю, визначається наступним виразом: u K П ( x 2 T x 2 ) KІ ( x 2 T x 2 )dt , (5) де x 2 T - уставка швидкості мехатронної системи; K 1 та K П - коефіцієнти підсилення інтегральної та пропорційної складових ПІ-регулятора відповідно, які визначаються за виразами: 25 A1 A 2 ; KП 2 6 (1 k1 k 2 k 3 ) (6) k3 K 1 K 2 П , І 2 1 k1 k 2 k 3 де A1, A 2, a,b, c - коефіцієнти, які визначаються із виразів 3 16 a 2 12c A1 3 3 2a3 27b 2 72ac 4 a 2 12c 2a3 27b 2 72ac 3 4(2a3 27b 2 72ac 4 a 2 12c 3 16 a 2 12c A2 3 3 2a3 27b 2 72ac 4 a 2 12c 2a3 27b 2 72ac 3 1 2 2 2a3 27b 2 72ac ) 4a , 3 2 8a 4(2a3 27b 2 72ac 4 a 2 12c 1 12 6b 2 , 2a3 27b 2 72ac ) A1 3 2 2 a 2k 3 (1 k1 k 2 k 3 ),b 8 k1(1 k1 k 2 k 3 )5 , 30 2 c (1 k1 k 2 k 3 )2 4k 2 (1 k1 k 2 k 3 ) k 3 . Згідно із пропонованим способом налаштування ПІ-регулятора для мехатронних систем спочатку встановлюють вагові коефіцієнт k1,k 2 та k 3 . Це робиться із врахуванням вимог, які ставляться до якості регулювання руху мехатронної системи: якщо необхідно, щоб мехатронна система швидко досягла уставки швидкості, то збільшують ваговий коефіцієнт k 1 ; якщо 2 UA 75909 U необхідно зменшити перерегулювання швидкості мехатронної системи, то збільшують ваговий коефіцієнт k 2 ; якщо необхідно зменшити навантаження на приводний механізм мехатронної 5 10 системи, то збільшують ваговий коефіцієнт k 3 . Надалі, згідно виразів (6) налаштовують коефіцієнти K П та K 1 . Після цього регулятор налаштований - його можна використовувати для регулювання руху мехатронної системи. Пропонований спосіб налаштування ПІ-регулятора для мехатронних систем може бути використаний для налагодження систем керування рухом роботів, кранів, ліфтів тощо. Використання пропонованого способу дозволить зменшити затрати праці при налаштуванні ПІрегуляторів, автоматично забезпечує асимптотичну стійкість об'єкту регулювання, зменшує динамічні навантаження у елементах приводу мехатронної системи та дає можливість експлуатувати привод без перевантажень. ФОРМУЛА КОРИСНОЇ МОДЕЛІ 15 20 Спосіб налаштування пропорційно-інтегрального регулятора для мехатронних систем, що мінімізує інтегральний тип критерію якості регулювання, який відрізняється тим, що встановлюють вагові коефіцієнти k1,k 2 та k 3 із врахуванням вимог, які ставляться до якості регулювання руху мехатронної системи; надалі задають величини коефіцієнтів підсилення інтегральної та пропорційної складових пропорційно-інтегрального регулятора у відповідності до виразів: A1 A 2 ; KП 2 6 (1 k1 k 2 k 3 ) k3 K 1 K 2 П , І 2 1 k1 k 2 k 3 де K П та K 1 - коефіцієнти підсилення інтегральної та пропорційної складових ПІ-регулятора відповідно; A1, A 2, a,b, c - коефіцієнти, які визначаються із виразів: 3 16 a 2 12c A1 3 3 2a3 27b 2 72ac 4 a 2 12c 2a3 27b 2 72ac 3 25 4(2a3 27b 2 72ac 4 a 2 12c 2a 3 3 27b 2 72ac 2 3 8a 4(2a3 27b 2 72ac 4 a 2 12c 2 1 2 12 6b 2 , 2a3 27b 2 72ac ) A1 3 1 2 ) 4a , 3 16 a 2 12c A2 3 3 2a3 27b 2 72ac 4 a 2 12c 2a3 27b 2 72ac 2 a 2k 3 (1 k1 k 2 k 3 ),b 8 k1(1 k1 k 2 k 3 )5 , 2 c (1 k1 k 2 k 3 )2 4k 2 (1 k1 k 2 k 3 ) k 3 , k1,k 2 та k 3 - вагові коефіцієнти, які враховують положення, швидкість та величину функції керування рухом мехатронної системи відповідно. 3 UA 75909 U Комп’ютерна верстка А. Крулевський Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601 4
ДивитисяДодаткова інформація
Назва патенту англійськоюMethod for tuning proportional-integral regulator for mechatronic systems
Автори англійськоюLoveikin Viacheslav Serhiiovych, Romasevych Yurii Oleksandrovych
Назва патенту російськоюСпособ настройки пропорционально-интегрального регулятора для мехатронных систем
Автори російськоюЛовейкин Вячеслав Сергеевич, Ромасевич Юрий Александрович
МПК / Мітки
МПК: G05B 11/36
Мітки: налаштування, мехатронних, систем, регулятора, пропорційно-інтегрального, спосіб
Код посилання
<a href="https://ua.patents.su/6-75909-sposib-nalashtuvannya-proporcijjno-integralnogo-regulyatora-dlya-mekhatronnikh-sistem.html" target="_blank" rel="follow" title="База патентів України">Спосіб налаштування пропорційно-інтегрального регулятора для мехатронних систем</a>
Попередній патент: Упаковка для споживчих виробів
Наступний патент: Офтальмологічний пристрій “масудкапсуло-рексис”
Випадковий патент: Фазовий регулятор змінного напруження