Шарнірний чотириланковий прямолінійно-напрямний механізм, побудований з використанням точки чебишева

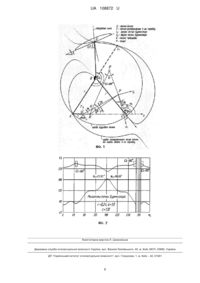
Реферат: Шарнірний чотириланковий механізм має основу, на якій встановлено кривошип, коромисло і шатун у вигляді двоплечого важеля, одне плече якого шарнірно зв’язано з кривошипом та коромислом, а інше плече виконано з можливістю опису його шатунною точкою кривої, яка на частковій ділянці траєкторії наближається до прямої лінії. За шатунну точку механізму прийнято точку Чебишева, яка визначається для заданих довжин кривошипа, шатуна та коромисла механізму як точка Болла в тому положенні шатунної площини, коли одна з двох точок Бурместера знаходиться на одній прямій з обома рухомими шарнірами механізму. UA 108872 U (54) ШАРНІРНИЙ ЧОТИРИЛАНКОВИЙ ПРЯМОЛІНІЙНО-НАПРЯМНИЙ МЕХАНІЗМ, ПОБУДОВАНИЙ З ВИКОРИСТАННЯМ ТОЧКИ ЧЕБИШЕВА UA 108872 U UA 108872 U 5 10 15 20 25 30 35 40 45 50 55 60 Корисна модель належить до машинобудування, а саме до проектування прямолінійнонапрямного механізму на основі шарнірного чотириланкового механізму, шатунна точка якого наближено описує на деякій ділянці пряму лінію при неперервному обертовому русі вхідної ланки (кривошипа). Одним з напрямків у синтезі таких механізмів є використання методів найкращого наближення за Чебишевим, що передбачають наявність максимально можливої кількості вузлів інтерполяції на ділянці наближення з рівномірним характером зміни відхилень [1,3]. Іншим напрямком є використання методів кінематичної геометрії, що полягають у пошуку таких вузлів інтерполяції, в яких збігаються декілька нескінченно близьких положень шатунної площини. Такі вузли інтерполяції називають кратними, вони характеризуються тим, що в даних точках збігаються не тільки самі функції (шатунної кривої та прямої лінії або кола), але й n їх похідних. В такому випадку функція буде мати дотик n -го порядку зі своїм дотичним колом або дотичною прямою. Вищі порядки дотику забезпечують краще наближення ділянки шатунної кривої відповідно до кола або прямої лінії. Синтез таких механізмів розглядається у роботах [2,4-8]. У кінематичній геометрії такими кратними вузлами інтерполяції є, зокрема, точки Болла, що визначаються для 4-х нескінченно близьких положень шатунної площини та забезпечують проектування прямолінійно-напрямних механізмів з дотиком 3-го порядку, а також точки Бурместера, за допомогою яких можна спроектувати кругові напрямні механізми з дотиком 4-го порядку (5 нескінченно близьких положень). При цьому в кінематичній геометрії описано частковий випадок [2,6,7], коли точка Болла в деякому положенні шатунної площини збігається з точкою Бурместера та забезпечує таким чином проектування прямолінійно-напрямних механізмів з дотиком 4-го порядку, що забезпечує краще наближення шатунної кривої до прямої лінії порівняно з точками Болла. Такий випадок називають випадком Чебишева, а відповідні точки Болла, що збігаються в даному положенні з точками Бурместера - точками Чебишева [2, с 345]. При цьому, в англомовній науковій літературі такі точки називають ще точками Болла-Бурместера [6-8]. В роботах Дж. Відосіча, Д. Тесара [6], Д. Тесара [7, с 15] синтез механізмів на базі точок Чебишева проводиться, виходячи із заданих полярних кутів, що визначають положення шарнірів механізму. Описані аналітичні методи та наведені діаграми дозволяють проводити синтез таких механізмів з врахуванням додаткових умов, проте цей метод не дозволяє проводити визначення точок Чебишева відповідно до заданих розмірів шарнірного чотириланкового механізму, оскільки розміри ланок визначаються в процесі проектування відповідно до інших умов. В роботі Я. Геронімуса [2, с. 351] наведено прямолінійно-напрямний шарнірний чотириланковий механізм, синтезований з використанням точки Чебишева (найближчий аналог). Положення шарнірів механізму визначені відповідно до заданого кута нахилу прямолінійної ділянки та положення шатунної точки, за яку приймається точка Чебишева. У найближчому аналогу передбачається, що розміри ланок механізму визначаються в процесі проектування та не можуть бути задані як вихідні дані для проектування. В основу заявленої корисної моделі поставлена задача - проектування прямолінійнонапрямного механізму на базі шарнірного чотириланкового механізму з використанням точок Чебишева за заданими розмірами ланок механізму (кривошипа, шатуна та коромисла) з наступним визначенням кута нахилу прямолінійної ділянки, що дозволяє розв'язати зворотну задачу порівняно з найближчим аналогом. Фіг. 1, 2 пояснюють запропоновану корисну модель. Фіг. 1. - Розрахункова схема прямолінійно-напрямного шарнірного чотириланкового механізму з точкою Чебишева як шатунної. Фіг. 2. - Приклад діаграми зміни кута  злому шатуна у механізмах, синтезованих за точками Бурместера (використовується для числового визначення точок Чебишева). Поставлена задача вирішується тим, що шарнірний чотириланковий механізм (фіг. 1) має основу 0, на якій встановлено кривошип 1, коромисло 3 і шатун 2 у вигляді двоплечого важеля, одне плече якого шарнірно зв'язано з кривошипом 1 та коромислом 3, а інше плече виконано з можливістю опису його шатунною точкою G кривої, яка на частковій ділянці траєкторії наближається до прямої лінії, причому за шатунну точку механізму приймається точка Чебишева, яка визначається для заданих довжин кривошипа 1, шатуна 2 та коромисла 3 механізму як точка Болла в тому положенні шатунної площини, коли одна з двох точок Бурместера знаходиться на одній прямій з обома рухомими шарнірами механізму. Оскільки точки Чебишева визначаються для часткового випадку положення шатунної площини механізму, коли точка Болла збігається з однією з точок Бурместера, то в кінематичній геометрії це відповідає випадку перетину в одній точці трьох кривих: поворотного кола, кривої 1 UA 108872 U кругових точок та кривої геометричного місця точок, які забезпечують дотик не нижче 4-го порядку зі своїми дотичними колами. Рівняння поворотного кола (в неявному вигляді): x 2  y 2  y" 0 y  0 , (1) 5 де y" 0 - прискорення полюса P миттєвого обертання шатунної площини механізму. Рівняння кривої кругових точок (в неявному вигляді): x 10 20 25   y 2 l1x  l 2 y   l 4 xy  0 , (2) де l1, l 2 , l 4 - коефіцієнти кривої. Рівняння кривої (в неявному вигляді), що являє собою геометричне місце точок, які забезпечують дотик не нижче 4-го порядку зі своїми дотичними колами: x 15 2 2   y 2 m 3  m 4 x  m 5 y   y" 0 ym1x  m 2 y  m 3   0 , (3) де m1 ... m5 - коефіцієнти кривої. Таким чином, якщо точка Чебишева, що визначається як точка перетину кривих (1), (2) та (3), буде прийнята за шатунну точку механізму, в результаті вона буде описувати шатунну криву, що на деякій своїй ділянці в околі цієї точки буде наближатись до прямої лінії з дотиком 4-го порядку. Розрахункова схема механізму показана на фіг. 1. Алгоритм проектування механізму наступний. 1. Задаємось довжиною кривошипа r  lO , шатуна b  l  та коромисла c  lBC . За модуль довжини прийнято відстань між осями нерухомих шарнірів d  l OC  1 . Кут 1 , що визначає положення кривошипа та відповідно шатунної площини механізму, будемо змінювати в циклі в діапазоні 1  0... 360  з певним кроком (наприклад, 1  1 ). Визначаємо координати точки А механізму (кінця кривошипа) для різних положень механізму:    r cos 1 ; Y  r sin 1 , (4) 2. Обчислюємо кути  2 та  3 , що визначають положення відповідно шатуна b коромисла механізму: c 30  2     ; 3       , (5) де   arctgYA /( X A  1);       . Для розрахунку шуканих кутів додатково визначаємо наступні величини:  b 2  2  c 2   arccos  2b  2 2   2  ,   arccos b  c     2bc    ;     2 1    2  Y , (6) 35 3. Обчислюємо координати точки B механізму:    1 c cos 3 ; Y  c sin 3 , 40 (7) 4. Обчислюємо координати полюса P миттєвого обертання шатунної площини та миттєвого полюса Q відносного руху шатуна 2 та коромисла 3 механізму:   tg  3  Y    Y ; Y    tg 1;  Q    ; YQ  0, tg  3  tg 1 Y  Y 5. Визначаємо прискорення полюса P миттєвого обертання шатунної площини механізму: 2 (8) UA 108872 U ' y '0   l O l O  l O  / l O sin  3   , (9) де кут нахилу осі колінеації   arctg Y / Y   Q , lO    / cos 1 . (9) 6. Визначаємо коефіцієнти кривої кругових точок (2): 5 l1   , k 1k 22  k 2k 12 k k  k 1k 21 ; l 2  2 11 ; l 4  3 y '' 0 k 11k 22  k 12 k 21 k 11k 22  k 12 k 21 2 (10) Коефіцієнти, що входять у (10) визначаються наступним чином:  x  ; k  x  ; k k 11  x  x 2  y 2 ; k 12  y  x 2  y 2 ; k 1  3 y '' x  y  ;     0 k 21  x  10 2   y2  22  y 2   y2  де координати шарнірів A та B в повернутій системі координат x1P' y1 : x        cos t  Y  Y  sin t , y   Yp  Y cos t   A  P  sin t ,   x  p   cos t  Y  Y  sin t , y  Yp  YB cos t  B  p  sin t , 15 (11)  3 y '' x  y  ; 0 2 (12) кут нахилу полюсної дотичної:  t  1  3   . 7. Визначаємо коефіцієнти кривої (3) геометричного місця точок, які забезпечують дотик не нижче 4-го порядку зі своїми дотичними колами: ' m1  4l2 ; m2 6y'0  4l1 ; m3  l4 ; m4  1  l1m1 ' 3y'0 ; m5   3  l1m2  l2m1 ' 3y'0 ., (13) Величини, що входять у (13) визначаються наступним чином: 1   4 x    5 y    2y2   3 x  y   x2    ' ;  2   l2m2 ;  4  l4 l1  3 y'0 . , (14) 20 3  25 x 2 2 y      (15) 8. Для знаходження точок Чебишева необхідно попередньо знайти в шатунній площині положення точок Бурместера, що визначаються як точки перетину кривих (2) та (3). Розв'язуючи сумісно рівняння цих кривих, записаних в неявному вигляді, отримаємо поліном четвертого степеня, корені якого і визначають точки Бурместера: n 4 x 4  n 3 x 3  n 2 x 2  n1x  n 0  0, 30   x 2 y 2  2  x 2 xB  x A x 2  4  x 2 yB  x 2 y A  5       ;  5  l2l4 , x  x  y  x   y  x   (16) де коефіцієнти полінома: n4   5l2 ; n3   2l4   4l2  5l1 ; n2  3l4   4l1  n4 ; n1  1l4   4l2  5l1 ; n0    4l1 . Рівняння (16), очевидно, має 4 корені, що визначають точки Бурместера. Два з них збігаються з рухомими шарнірами А та В механізму, тому: x1  tg1  3  ; x 2   tg  , (17) 3 UA 108872 U де  - кут, що визначає напрямок полюсної дотичної. Два інших корені полінома (16) можуть бути використані при проведенні синтезу: x3,4  5 (18) де p  n3 / n4  x1  x2; q  n2 / n4  x1x2  p( x1  x2 ). Таким чином, координати обох точок Бурместера, що не збігаються з рухомими шарнірами механізму: x S1  10  p  p 2  4q , 2  4   5x3 1   3 x3  2  2x3 ; y S1  x S1 x 3 ; x S2   4  5x4 1   3 x 4   2x2 4 ; y S2  x S2 x 4 . , Для того, щоб отримати положення точок Бурместера у базовій системі координат хОу, проведемо зворотне перетворення системи координат за формулами:  S1     x S1 cos  t  y S1 sin  t , YS1  Y  y S1 cos  t  x S1 sin  t ,  S2     x S2 cos  t  y S2 sin  t , YS2  Y  y S2 cos  t  x S2 sin  t 15 (19) , (20) Визначивши положення точок S1 та S 2 , можна знайти кути злому шатуна, що відповідають кожній з цих точок:  180    YS1,2  Y   , 0    360  ,    2  arctg    S      1, 2    (21) Слід зазначити, що для деяких положень шатунної площини точок Бурместера може не виявитись. 20 25 9. Розрахувавши точки Бурместера для всіх положень механізму 0  1  360  , будуємо графік залежності кута  злому шатуна від кута 1 , що визначає положення кривошипа та відповідно шатунної площини, для якого визначалось положення точок Бурместера. Приклад такого графіку для певних значень довжини кривошипа, шатуна та коромисла показано на фіг. 2 (заштрихована область відповідає положенням шатунної площини, для яких точки Бурместера відсутні, значення у прямокутниках відповідають величинам, які необхідно зменшити на 180°). 10. Визначаємо чисельно значення кутів повороту кривошипа 1 що відповідають точкам Бурместера, для яких кут злому шатуна   180  , оскільки точки Болла, визначені для положень шатунної площини, що відповідають цим кутам повороту кривошипа будуть точками Чебишева. Як видно з фіг. 2, в даному прикладі для заданих розмірів механізму було знайдено 30 дві точки Чебишева: для положень 1  177,93  та  '  190,19  . 1 11. Визначаємо положення точок Чебишева як точок Болла, що збігаються в даному положенні з точками Бурместера: ' ' xG  Ry '0', yG  Rx '0', 35 40 (22)     ' '  ' 2 ' 2 ' ' ' R  x '0' y '0 /  x '0'  y '0'  ; x '0'  l1  3y '0 ; y '0'  l 2 . Як видно з фіг. 1 знайдена точка   Чебишева, крім того, збігається з точкою розпрямлення 4-го порядку. Величини, що входять у (22), необхідно розрахувати відповідно до значень 1 , які визначені у п. 10. Для цього необхідно зробити відповідні розрахунки за формулами (4)-(12). 12. Визначаємо положення точки Чебишева G у базовій системі координат хОу. Для цього проведемо перетворення системи координат за наступними формулами: де 4 UA 108872 U XG  Xp  xG cos t  yG sin t ; YG  Yp  yG cos  t  xG sin  t , (23) 13. Проектуємо важільний чотириланковий механізм, у якому довжина другого плеча шатуна k  lBG та. кут  G його злому визначає положення шатунної точки, за яку буде прийнята знайдена точка Чебишева: 5 k  lG  G  180  G   2  YG  Y 2 ,   YG  Y    2  arctg       G  (24)   , 0   G  360  ,    (25) 14. Кут нахилу прямолінійної ділянки шатунної кривої:  Y  Y  y'' cos   G 0 t ,   arctg        y'' sin   G 0 t   (26) 10 15 20 25 30 Джерела інформації: 1. Артоболевский И. И. Синтез плоских механизмов./ И. И. Артоболевский, Н. И Левитский, С. А. Черкудинов - М.: Физматгиз, 1959. - 1084 с. 2. Геронимус Я. Л. Геометрический аппарат теории синтеза плоских механизмов. - М.: Гос. издательство физ.-мат. литературы, 1962. - 400 с. 3. Киницкий Я.Т. Шарнирные механизмы Чебышева с выстоем выходного звена / Я. Т. Киницкий. - К.: Вища школа, 1990. - 232 с. 4. Харжевський В.О. Синтез важільних прямолінійно-напрямних механізмів та механізмів із зупинкою вихідної ланки на базі шарнірного чотириланкового механізму: дис…канд. техн. наук: 05.02.02 / В.О. Харжевський; Хмельницький держ. ун-т. - Хмельницький, 2004. - 262 с. 5. Харжевський В.О. Аналітично-числовий синтез кругових напрямних механізмів на базі шарнірного чотириланкового механізму з використанням точок Бурместера. / В.О. Харжевський, Я.Т. Кіницький //Машинознавство, Львів: Вид-во КІНПАТРІ. - 2005. - С. 61-65. 6. Vidosic J., Tesar D. Selection of four-bar mechanisms having required approximate straight-line outputs. Part I. The general case of the Ball-Burmester point /Journal of mechanisms, 2(1), 1967, pp. 23-44. 7. Tesar D. The analytical theory of coplanar motion applied to approximate four-bar straight line mechanisms. PhD dissertation. Georgia Institute of Technology, Atlanta, USA, 1964. - 178 p. 8. Wang D. Kinematic Differential Geometry and Saddle Synthesis of Linkages /Wang D.,Wang W. – John Wiley & Sons Singapore Pte., 2015 - 450 p. ФОРМУЛА КОРИСНОЇ МОДЕЛІ 35 40 Шарнірний чотириланковий механізм, що має основу, на якій встановлено кривошип, коромисло і шатун у вигляді двоплечого важеля, одне плече якого шарнірно зв'язано з кривошипом та коромислом, а інше плече виконано з можливістю опису його шатунною точкою кривої, яка на частковій ділянці траєкторії наближається до прямої лінії, причому за шатунну точку механізму приймається точка Чебишева, яка визначається для заданих довжин кривошипа, шатуна та коромисла механізму як точка Болла в тому положенні шатунної площини, коли одна з двох точок Бурместера знаходиться на одній прямій з обома рухомими шарнірами механізму. 5 UA 108872 U Комп’ютерна верстка Л. Ціхановська Державна служба інтелектуальної власності України, вул. Василя Липківського, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут інтелектуальної власності”, вул. Глазунова, 1, м. Київ – 42, 01601 6