Роторний кидач ґрунту
Формула / Реферат
Роторний кидач ґрунту, що містить радіально закріплені на ступиці лопатки, який відрізняється тим, що лопатка виконана із профілем оптимальної форми - брахістохрони в полі відцентрових сил, яка описується рівнянням:
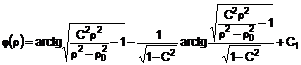 ,
,
де ![]() ,
, ![]() - полярні координати кривої в системі координат, полюс якої співпадає з центром обертання ротора;
- полярні координати кривої в системі координат, полюс якої співпадає з центром обертання ротора;
![]() ,
, ![]() - початкові координати;
- початкові координати;
![]() ,
, ![]() - константи, що визначаються умовою
- константи, що визначаються умовою ![]() при
при ![]() .
.
Текст
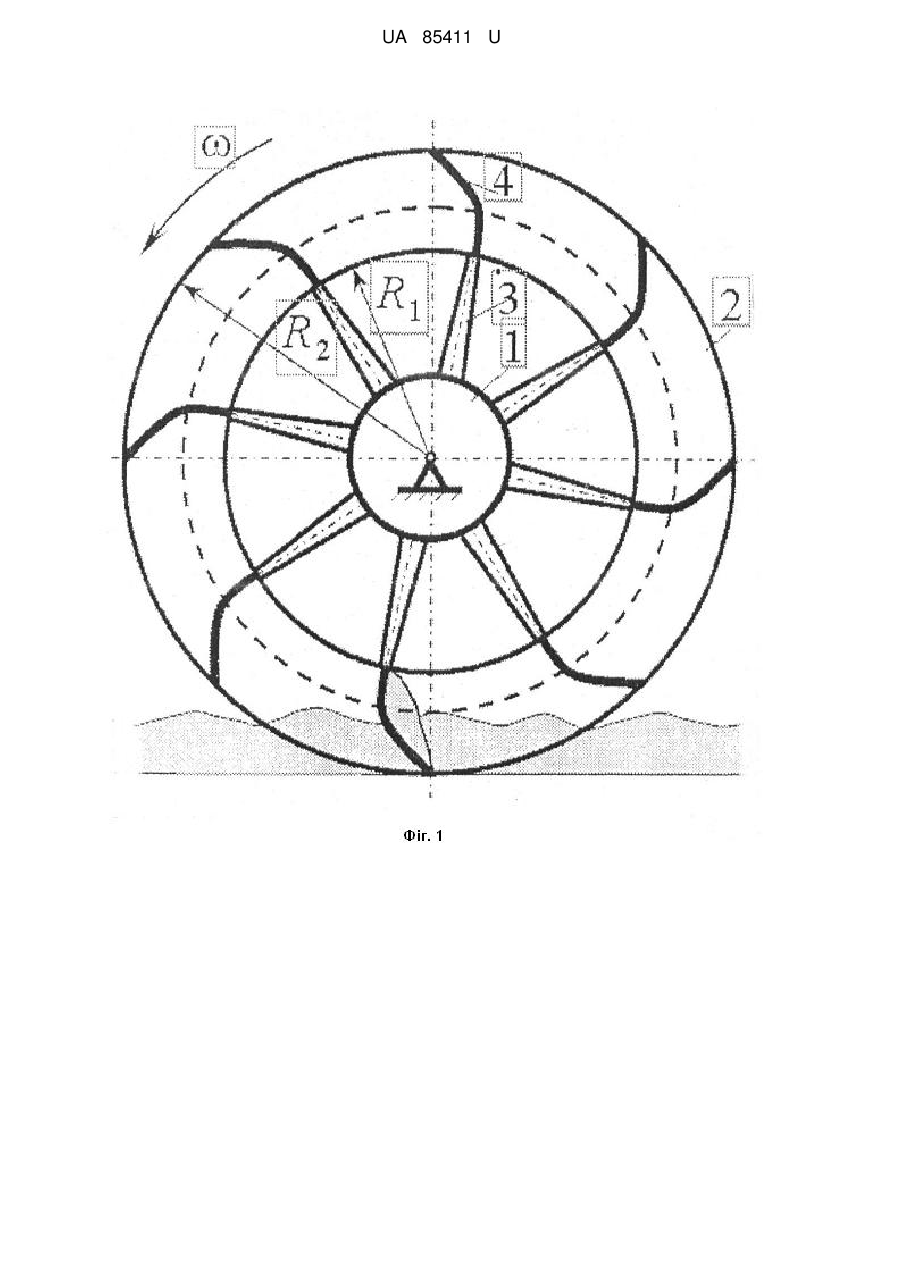
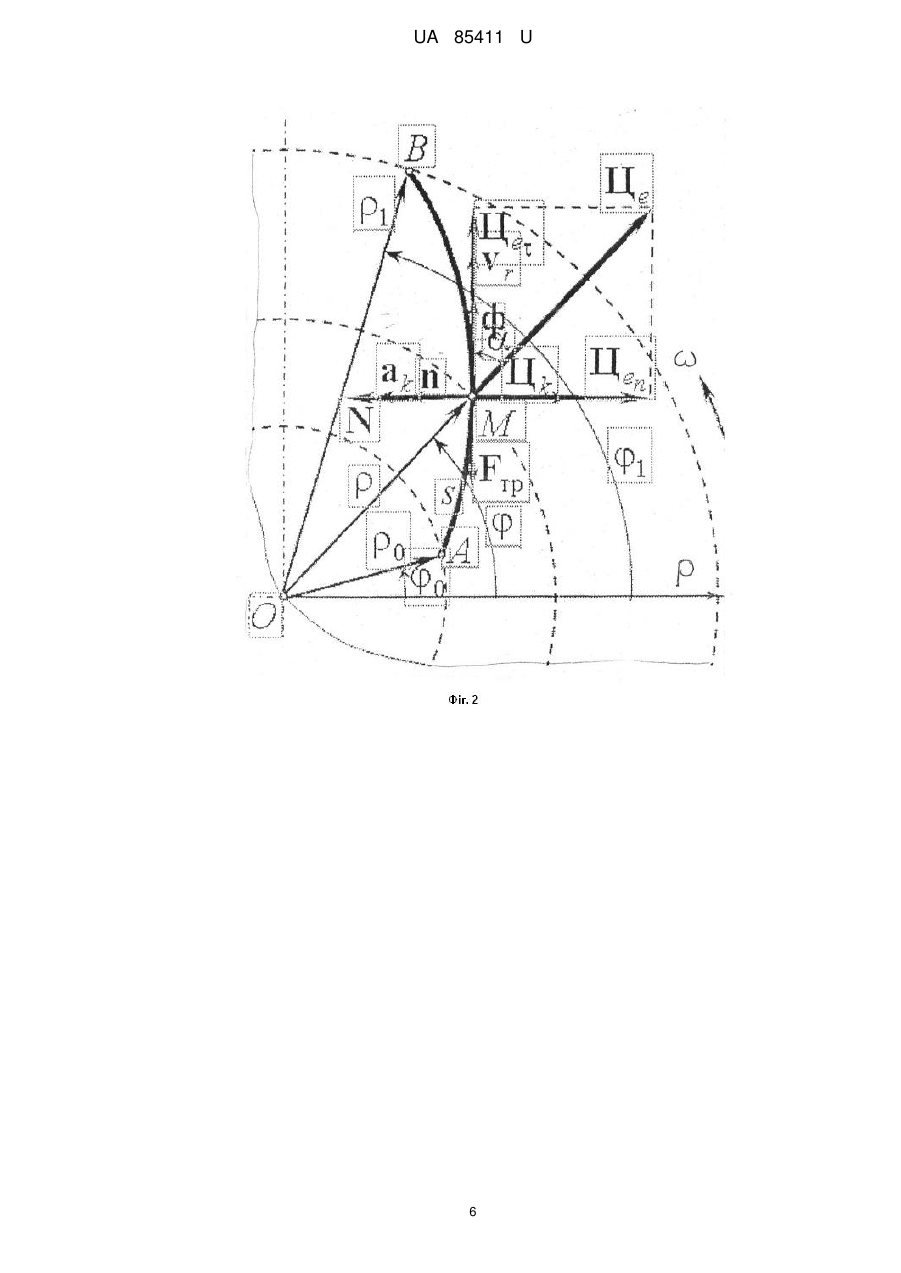
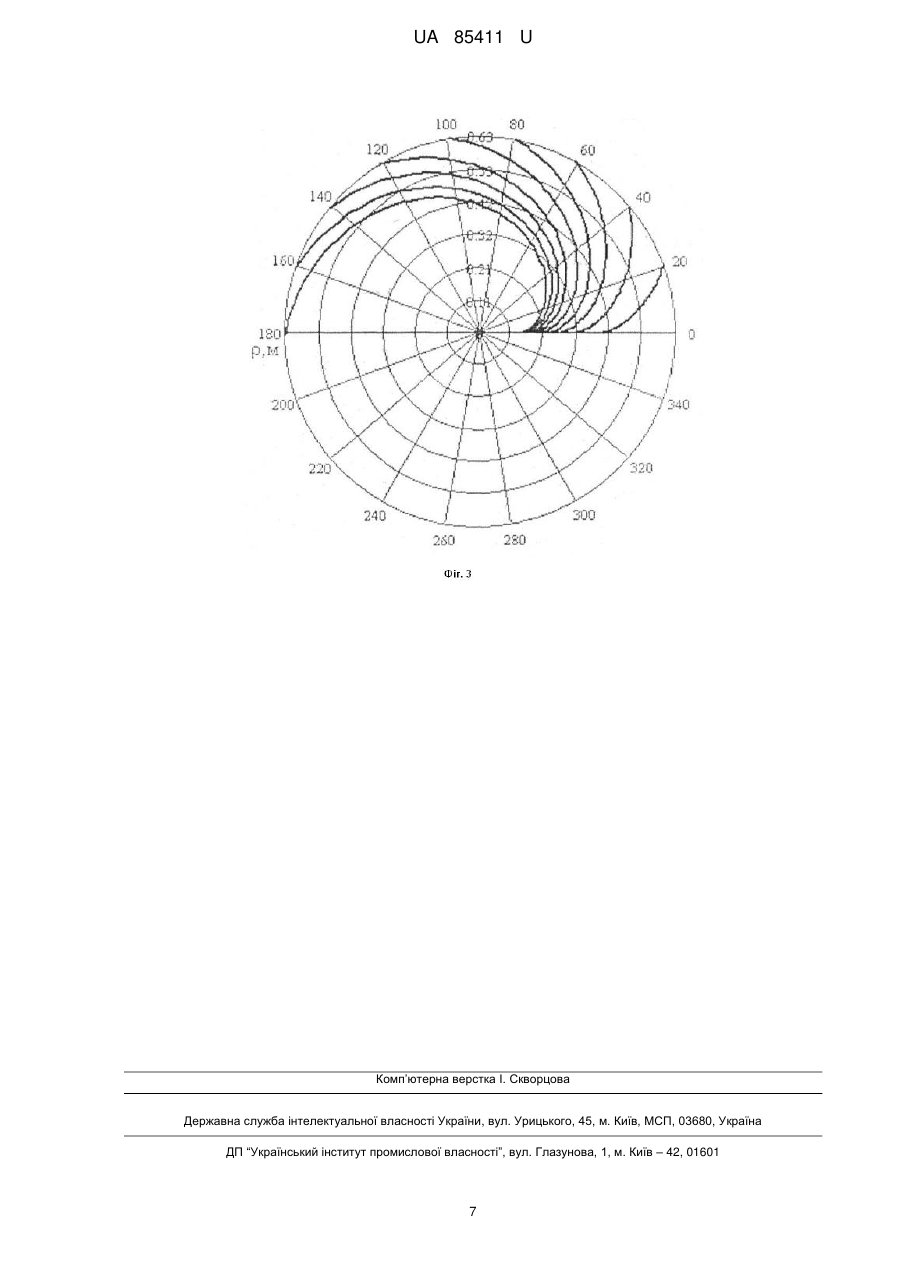
Реферат: UA 85411 U UA 85411 U 5 10 15 20 Корисна модель належить до землерийних машин з роторними робочими органами, призначеними здебільшого для боротьби з низовими лісовими пожежами методом метання ґрунту і прокладання загороджувальних мінералізованих смуг. Відомі землерийно-метальні машини з робочими органами у вигляді лопаток, радіально закріплених на привідному роторі [1, 2]. Недоліком таких машин є недостатня швидкість ґрунту в момент метання і відповідно невисока дальність кидання. Найбільш близьким до пропонованого і вибраним за прототип є роторний метальник [3], що містить консольно розташований на підшипниковій опорі вертикальний диск з радіально закріпленими лопатями і ґрунтоутримуючими лопатками, причому диск по колу виконаний з нормально направленими до кінців лопатей Г-подібними вирізами, в яких розташовані ґрунтоутримуючі лопатки, з'єднані з диском за допомогою розміщених паралельно лопатям осей і пружин кручення, а підшипникова опора має упор, розташований з можливістю взаємодії з вертикальними роликами і зворотно-поступального повороту ґрунтоутримуючих лопаток. Недолік цього метальника полягає в невеликій швидкості кидання ґрунту та відповідно недостатній дальності метання. Це пов'язано з тим, що форма лопаток не є оптимальною (не забезпечує мінімальну тривалість руху частинок ґрунту по лопатці). Окрім зазначеного недоліку, метальник має складну багатодетальну конструкцію. В основу корисної моделі поставлено задачу створити роторний метальник ґрунту з лопатками оптимальної форми, що дозволяє отримати максимальну швидкість ґрунту в момент кидання. Поставлена задача вирішується тим, що в роторному метальнику ґрунту, котрий містить радіально закріплені на ступиці лопатки, лопатка виконана із профілем оптимальної форми брахістохрони в полі відцентрованих сил інерції, яка описується рівнянням C22 arctg 25 30 35 40 45 50 55 C22 2 2 0 1 1 1 C2 arctg 2 2 0 1 C2 1 C1 , де φ, ρ - полярні координати кривої в системі координат, полюс якої співпадає з центром обертання ротора; φ0, ρ0 - початкові координати; с, с1 - константи, що визначаються умовою φ=φ0 при ρ=ρ0. На фіг. 1 показана схема ґрунтокидача, де цифрами позначено: 1 - ступиця; 2 - кільце; 3 спиця; 4 - криволінійна лопатка. Передбачається, що кидач обертається з кутовою швидкістю ω проти ходу годинникових стрілок. Радіуси R1 і R2 проходять через задню й передню крайки лопатки. Специфіка завдання полягає в тому, що рух необхідно вивчати в обертовій системі координат з використанням рівнянь динаміки відносного руху. Аналітичний опис оптимальної траєкторії одержано в полярній системі координат ρ=ρ(φ), (1) де ρ - полярний радіус; φ - полярний кут. Ha фіг. 2 частка ґрунту Μ зображена в поточному положенні з координатами (ρ,φ) на криволінійній лопатці АВ. Точки А і В мають відповідно координати (ρ0, φ0) і (ρ1,φ1). У викладеній нижче теорії полярним радіусам ρ0 і ρ1 відповідають радіуси R1 й R2. Для прийнятого напрямку обертання ротора ґрунтокидача вектор кутової швидкості щ буде перпендикулярний площини рисунка й спрямований на читача. Використано наступні позначення: ф - дотична, спрямована убік зростання дугової координати s; n - нормаль, спрямована убік увігнутості траєкторії; vr - відносна швидкість; аk=2щ×vr - коріолісово прискорення. Для сил прийняті такі позначення: Це - переносна (відцентрова) сила інерції; Цk - коріолісова сила інерції; Ν - нормальна реакція лопатки; Fтр - сила тертя ковзання (спрямована проти відносної швидкості). Вирази для модуля сили Це і її проекції на напрямок полярного радіуса збігаються Фе Фер ma m2 , (2) де m - маса частки ґрунту; 2 αω=ω ρ - осевідцентрове (нормальне) прискорення. Для коріолісової сили інерції має місце формула Цk=-mаk, (3) а для її модуля з урахуванням виразу для коріолісового прискорення Φk=2mωνr, (4) 1 UA 85411 U де vr vr vr 5 - модуль відносної швидкості; ds dt - проекція відносної швидкості на дотичну (алгебраїчна величина швидкості). Модулі сили тертя й нормальної реакції зв'язані відомим співвідношенням Fтр=Nf, (5). де f - коефіцієнт тертя ковзання. Для проекцій переносної (відцентрової) сили Це на дотичну Фе й нормаль Феn мають місце формули Фе Фе cos ; (6) Феn Фе sin , (7) 10 де α - кут між вектором Це і одиничним вектором дотичній ф. Можна показати, що для cosα й sinα справедливі вирази cos 2 2 ; (8) sin 2 2 . (9) Диференціальні рівняння відносного руху невільної матеріальної точки в природній формі при русі в площині будуть мати вигляд. mar Фе Fтр mar N Феn Фk n ; , (10) 15 a де r , a r - проекції прискорення на дотичну й нормаль. З урахуванням формул для дотичного й нормального прискорень n ar dvr dt d2s dt2 , (11) an 2 2 v 2 vr 1 ds k k k dt , (12) рівняння можна записати інакше m 20 d2s dt2 2 Фе Nf m ds N Феn Фk k dt ; , (13) де ρk - радіус кривизни траєкторії. Перетворимо рівняння (13) до рівняння для знаходження закону руху частки з обліком того, що рівняння траєкторії виявилося доцільним визначати в полярній системі координат. Довжина дуги й радіус кривизни кривої (1) визначаються відповідно по формулах: 25 0 ds k ' d 2 2 ; (14) 2 '2 3 2 2 22 , (15) 2 d d d2 . d , де Вираз для алгебраїчної величини швидкості й дотичного прискорення представимо так: vr ar 30 0 s s ds ds d ds dt d dt d ; (16) dvr dt d2s dt2 2 d2s d ds d2 d2s 2 ds d dt2 d2 d , (17) d2 dt де точкою позначена похідна за часом. Із другого рівняння (13) для нормальної реакції з обліком (4), (7), (9), (12), (15), (16) і (17) маємо 2 N m k 2 ds 22 ds 2 d d 2 2 , (18) Перепишемо тепер перше рівняння (13) з урахуванням формул (2), (8), (17), (18) 2 d2s ds 2 m 2 2 m m d k 2 2 d ( 35 2 ds 22 ds 2 f d d 2 2 . (19) Розділивши обидві частини виразу (19) на m, після нескладних перетворень, йому можна додати вид однорідного диференціального рівняння другого порядку зі змінними коефіцієнтами щодо полярного кута φ(t) 2 UA 85411 U ds d 5 1 2 1 ds 2 22 2 ds 2 f f 2f 0 3 d2 d d 2 2 2 2 2 . (20) d2s Рівняння (20) необхідно інтегрувати з початковими умовами: при t 0 0 , 0 . Завдання вибору оптимальної форми лопатки може бути схематизоване, як завдання визначення форми кривої у поле відцентрових сил інерції, що забезпечує мінімальний час руху (завдання про брахістохрону в полі відцентрових сил). Відомо, що класичне завдання про брахістохрону для однорідного поля сил ваги була відправною точкою при створенні варіаційного числення. Скористаємося одним з типів кривих, отриманих у результаті розв'язання такого завдання. 1 arctgz 10 arctg 2 1 C z 1 C2 C1 , (21) де z C22 2 2 0 1 , (22) 2 С
ДивитисяДодаткова інформація
МПК / Мітки
МПК: B65G 31/00, E02F 3/00
Мітки: кидач, ґрунту, роторний
Код посилання
<a href="https://ua.patents.su/9-85411-rotornijj-kidach-runtu.html" target="_blank" rel="follow" title="База патентів України">Роторний кидач ґрунту</a>
Попередній патент: Спосіб хірургічного лікування норицевої форми остеоартропатії при синдромі діабетичної стопи
Наступний патент: Штамп для формування канавок на трубі
Випадковий патент: Циліндро-конічний танк для зброджування пива