Спосіб роботи np-процесора

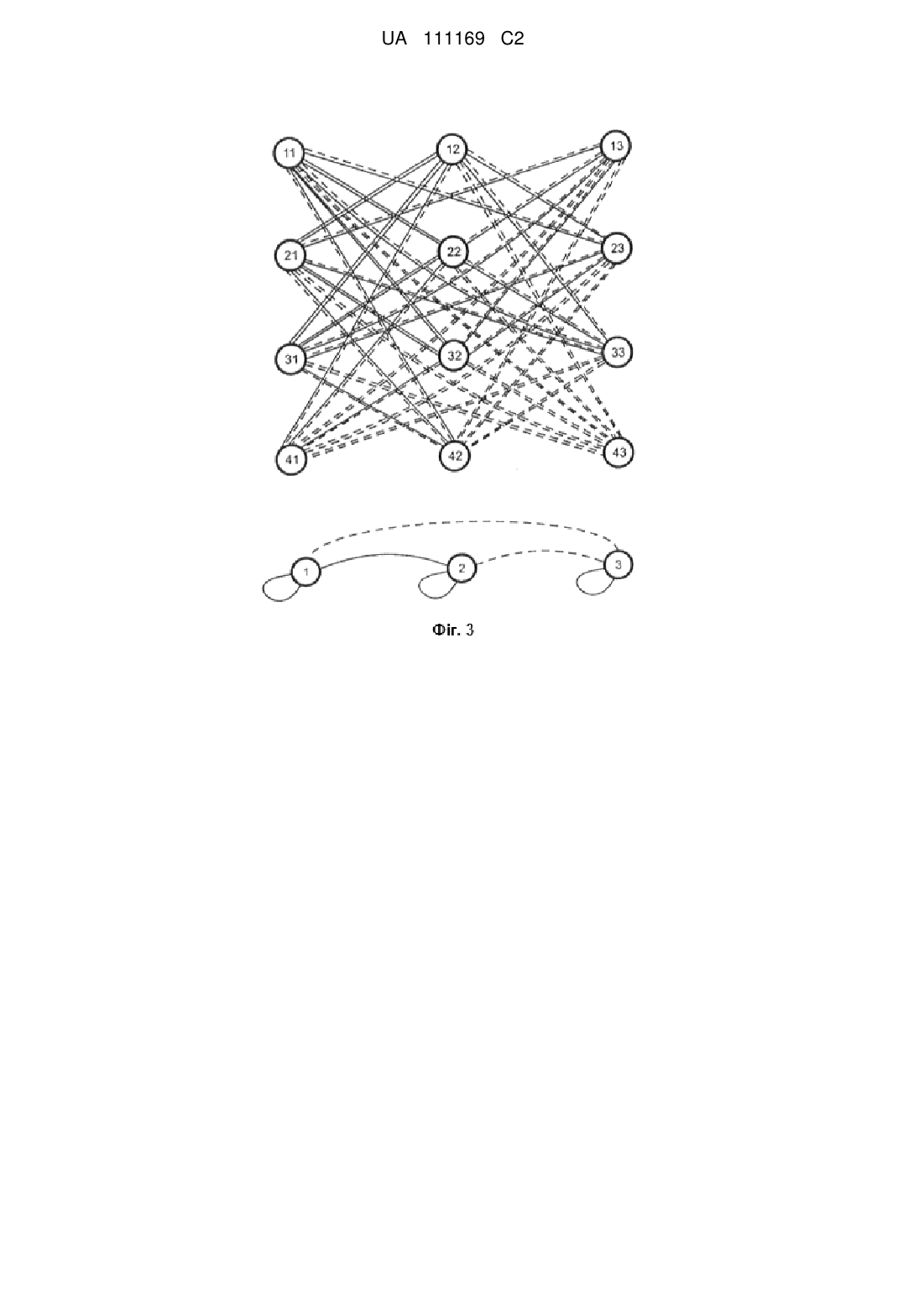
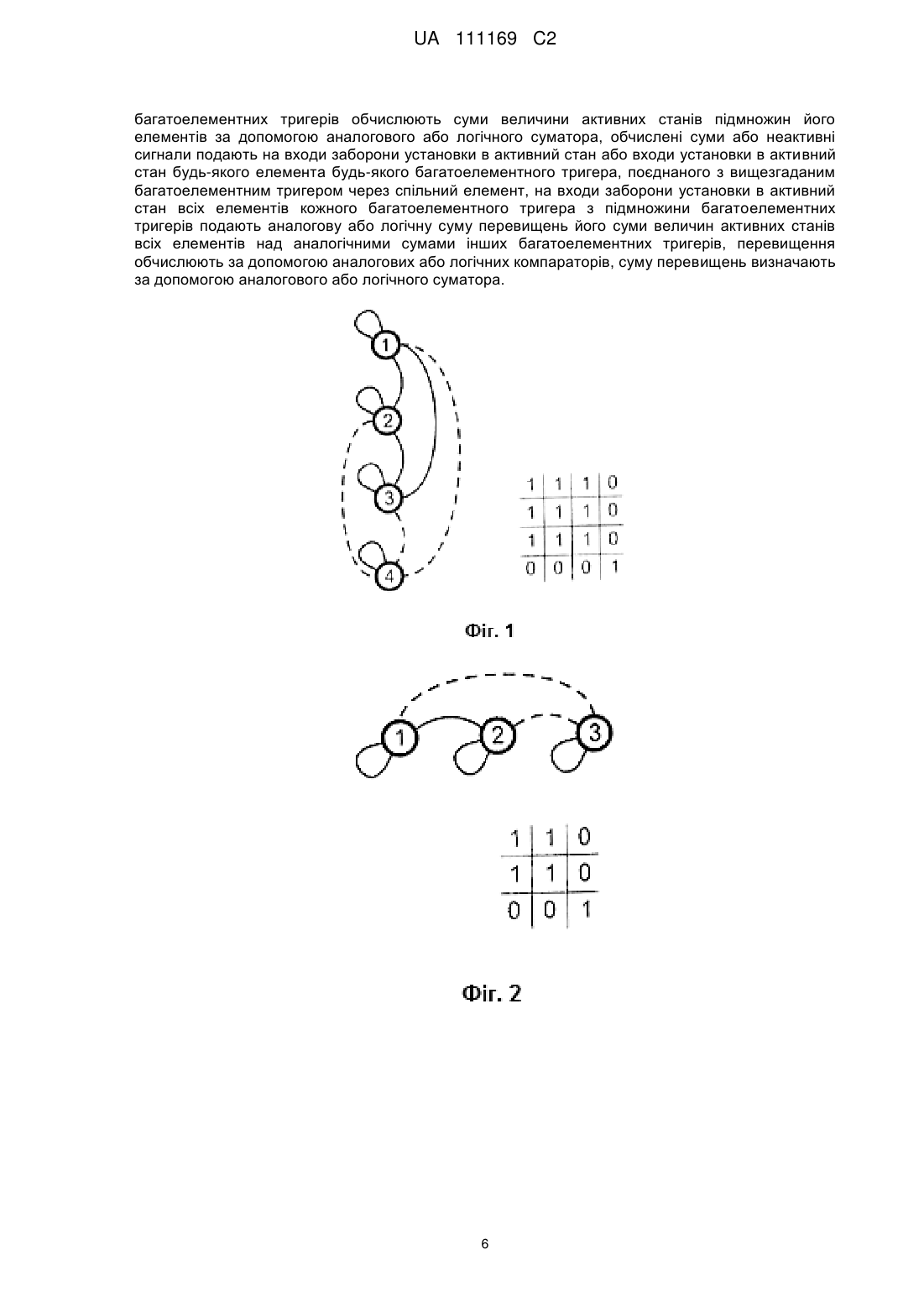
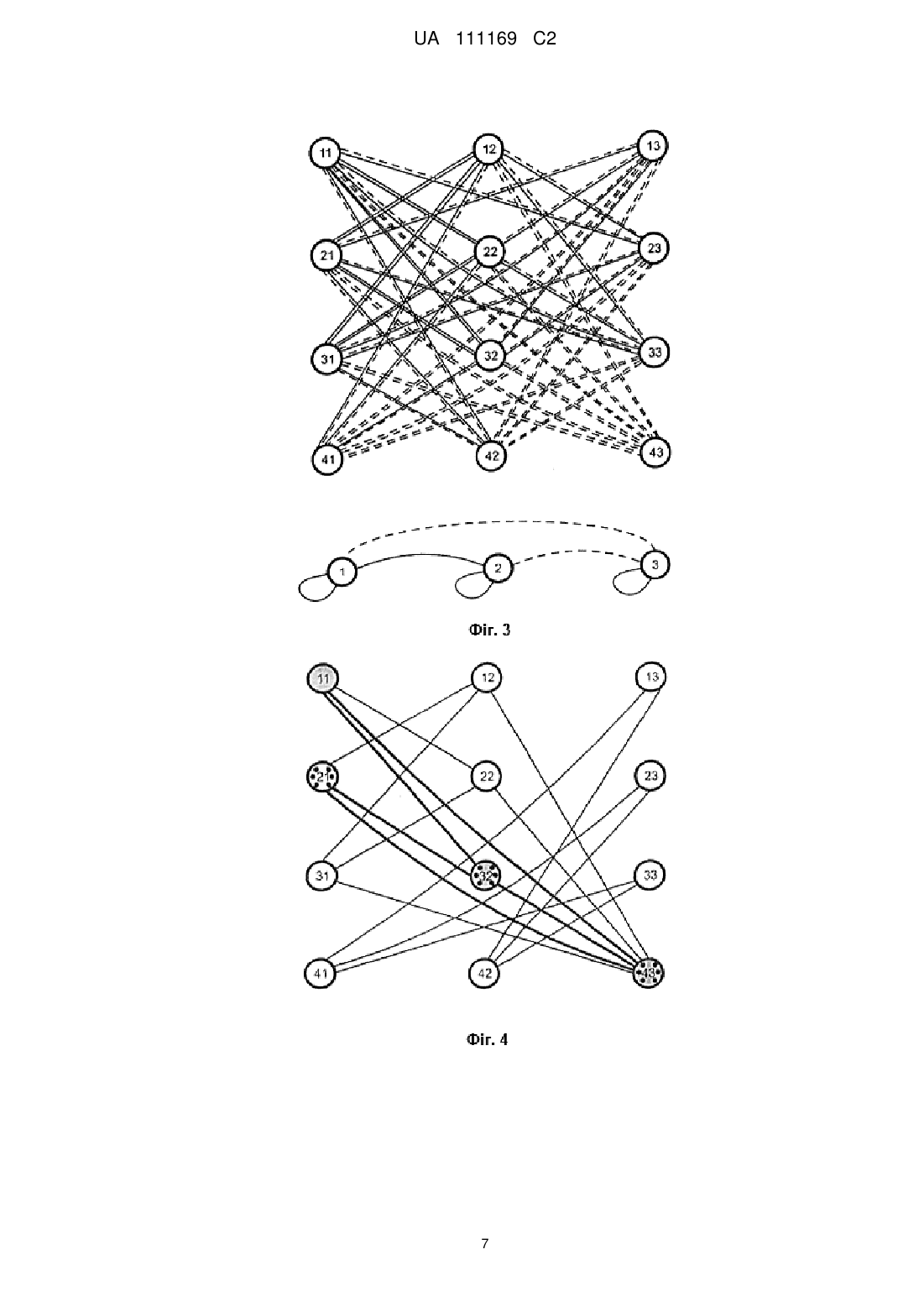
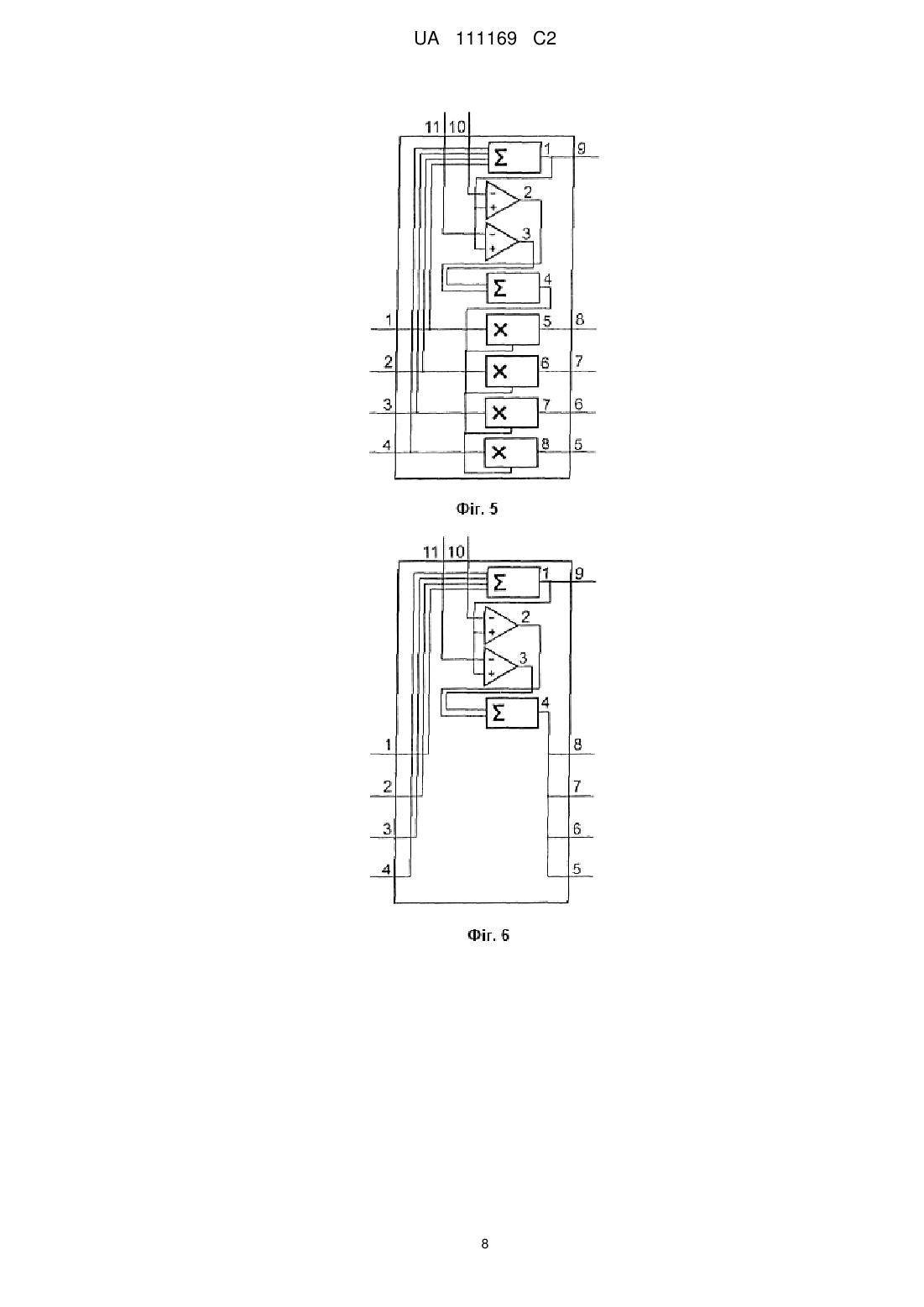
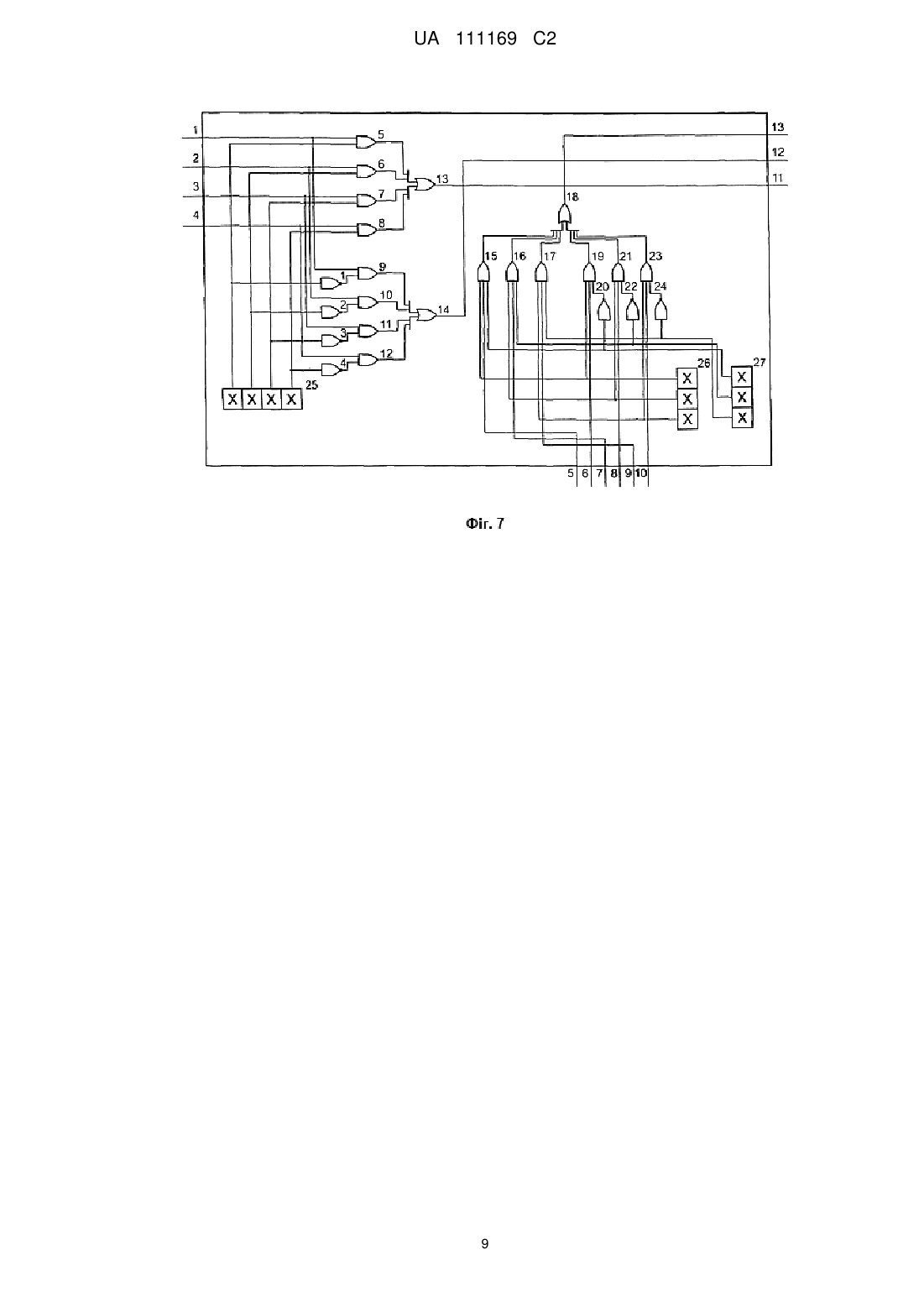
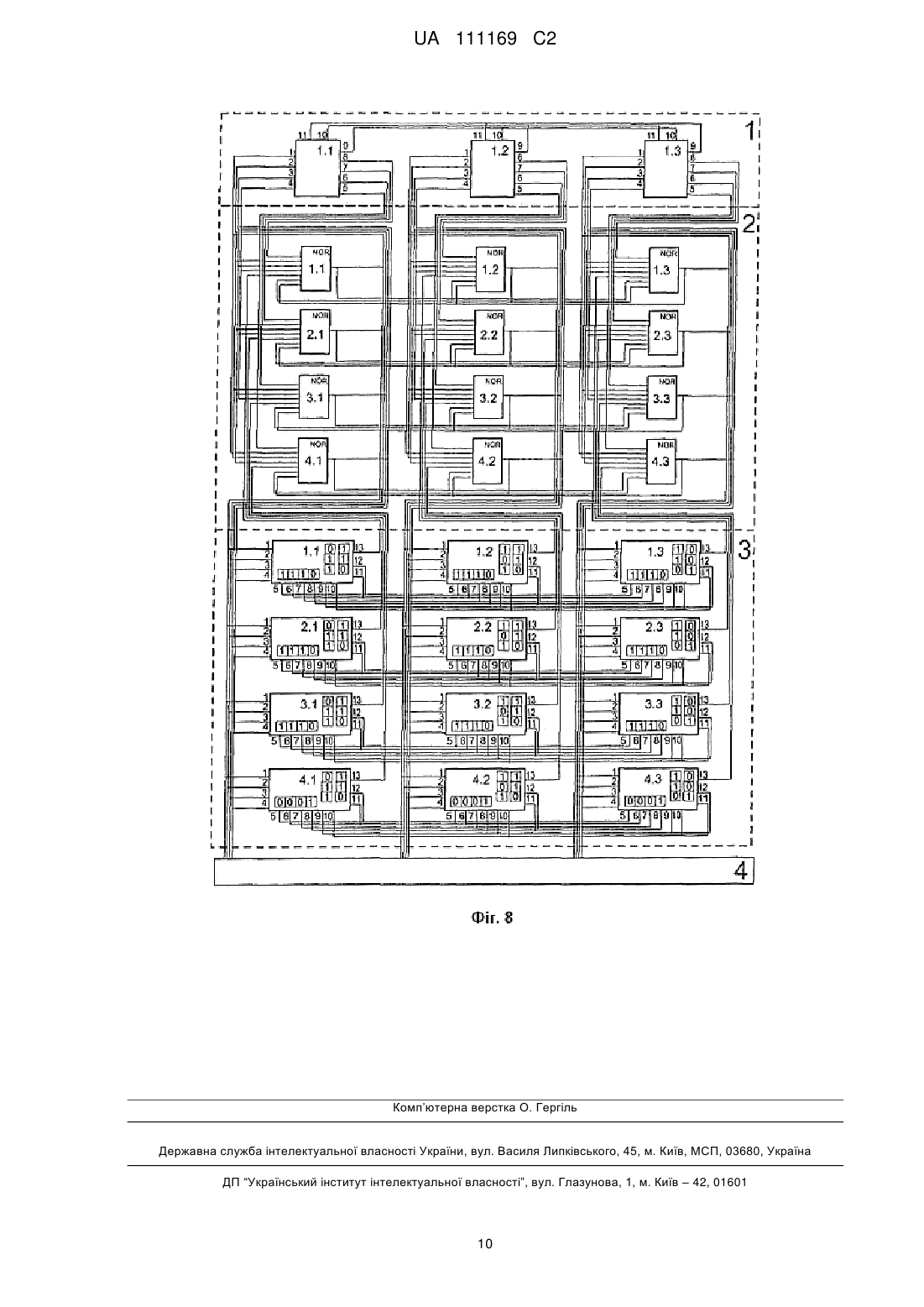
Реферат: Винахід належить до області комп'ютерної техніки та може бути використаний як процесор або співпроцесор для вирішення експоненціально-складних задач (NP-задач) за час, поліноміально залежний від об'єму вхідних даних. Спосіб роботи NP-процесора побудовано на основі обчислювального середовища, що складається із кінцевої множини багатоелементних тригерів, з'єднаних спільними елементами. Відповідно до винаходу в NP-процесор введені, залежні від умов задачі, інтерференційні зв'язки між елементами обчислювального середовища і, не залежні від умов задачі, від'ємні зворотні зв'язки для динамічного вирівнювання активності елементів обчислювального середовища. Введені зв'язки призначені для виділення з експоненціального числа форм коливань в обчислювальному середовищі стаціонарного стану, що є вирішенням задачі. UA 111169 C2 (12) UA 111169 C2 UA 111169 C2 5 10 15 20 25 30 35 40 45 50 55 60 Винахід належить до області комп'ютерної техніки та може бути використаний як процесор або співпроцесор для вирішення експоненціально-складних задач (NP-задач) за час, поліноміально залежний від об'єму вхідних даних. Основне призначення винаходу - побудова на його основі систем штучного інтелекту. Сучасні комп'ютери, що побудовані на алгоритмічних принципах, ефективно розв'язують всі задачі, для яких створюються алгоритми у вигляді програм. Але крім алгоритмічно розв'язуваних задач є великий клас задач, для яких не існує алгоритмів з обсягом обчислень, що росте повільніше, ніж експонента від об'єму вхідних даних, - це NP (non polynomial tasks) задачі. Серед них особливе місто займають NP-повні задачі, до будь-якої з них зводяться усі інші NP-задачі. Тому процесор, що розв'язує одну з NP-повних задач, буде універсальним NPпроцесором. Задачею винаходу є побудова NP-процесора для розв'язання NP-повної задачі пошуку в графі частини, ізоморфної заданому графу. Математичною основою для побудови NP-процесора є добуток графів, вперше запропонований Vizing, V. G. ("Reduction of the problem of isomorphism and isomorphic entrance to the task of finding the nondensity of a graph", Proc. 3rd All-Union Conf. Problems of Theoretical Cybernetics, 1974, p. 124.). Незалежно, аналогічний результат було одержано Новіковим А.А. відносно до задач розпізнавання образів ("Выделение частей в графе отношений, изоморфных заданному графу", Республиканский межведомственный научно-технический сборник, Проблемы бионики, вып. 21. - К.: Выща школа, 1978. - с. 129). Там же висловлено припущення, якщо добуток графів визначає зв'язки нейронів у ансамблі, то множина нейронів, зв'язки котрих визначаються повним графом, більш схильна до збудження, що може бути підтвердженням існування на нейронному рівні механізмів розв'язання вищезгаданої задачі. Абстрактним пристроєм, що вирішує NP-задачі за поліноміальний час, є недетермінована машина Тюринга (Карпов Ю.Г., 2003, Теория автоматов, Питер, 208 с.). В патенті (US20050013531) запропонована реалізація недетермінованої машини Тюринга на основі паралельних оптичних обчислень. Але електронна повнофункціональна реалізація поки що не одержана. NP-процесор, що пропонується, також як і недетермінована машина Тюринга, створює для кожної гілки задачі свою машину, тільки віртуальну, складену з елементів кінцевої множини шляхом їх комбінування. Кількість віртуальних машин так же експоненційно залежить від кількості елементів цієї множини, як і обсяг обчислень для розв'язання NP-задачі від кількості вхідних даних. Кількість елементів для побудови віртуальних машин поліноміально залежить від кількості вхідних даних. Експоненціальна кількість віртуальних машин розв'язує експоненціальної складності задачу за поліноміальний час. Віртуальні машини конкурують (інтерферують між собою) у взаємній суперпозиції. Рішенням є машина, що збереже задану кількість елементів у активному стані. Такий підхід є єдиним, що дозволяє не порушуючи фундаментальних результатів теорії складності алгоритмів (Christos H. Papadimitriou, 1994, Computational Complexity, Addison-Wesley.), розв'язувати NP-задачі за поліноміальний час. Розглянемо роботу NP-процесора на простому прикладі з невеликою кількістю вхідних даних. Це два графи: один з трьома вершинами, другий з чотирма. Графи задані своїми матрицями суміжності (Фіг. 1, 2). Будемо шукати частину чотиривершинного графа, співпадаючу з тривершинним. Для зручності подальшого розгляду, відсутність зв'язку між вершинами графа, відповідна нулю в матриці суміжності, у графічному представленні графів зображується пунктирною лінією між цими вершинами. Побудуємо допоміжний граф, що складається із дванадцяти вершин, тобто чотирьох вершин чотиривершинного графа, розміщених у вигляді вертикальних стовбців, повторених три рази. Поєднаємо вершини усіх пар стовбців так, як вони зв'язані у вищезгаданому чотиривершинному графі, а вершини усередині стовбців зв'язувати не будемо (Фіг. 3). Розмістимо, горизонтально, під допоміжним графом три вершини тривершинного графа з відповідними ребрами. Проіндексуємо вершини кожного стовбця допоміжного графа, узявши другим індексом номер вершини тривершинного графа, що знаходиться під індексованим стовбцем. Потім кожним ребром тривершинного графа поєднаємо попарно (суцільною або пунктирною лінією) відповідні вершини кожних двох стовбців допоміжного графа (Фіг. 3). Наприклад, перша вершина і друга вершина тривершинного графа зв'язані суцільною лінією, тоді зв'яжемо суцільною лінією кожну пару вершин першого і другого стовбців допоміжного графа з неспівпадаючими першими цифрами індексів. 1 UA 111169 C2 5 10 15 20 25 30 35 40 45 50 55 60 Побудуємо граф - добуток чотиривершинного графа і тривершинного за наступним правилом. Якщо ребра допоміжного графа і тривершинного графа співпадають (суцільна лінія із суцільною або пунктирна із пунктирною), замінимо їх просто ребром, якщо не співпадають, нічого не рисуємо. У підсумку отримаємо добуток графів (Фіг. 4). Проаналізуємо, яку структуру отримано між вершинами 11, 32, 43 і 21, 32, 43, добутку графів, виділивши вершини графа цієї частини сірим кольором і крапками (Фіг. 4). У кожному з двох наборів пар цифр перша цифра вказує, на вершину чотиривершинного графа, з якою повинна бути співставлена вершина тривершинного графа, для того, щоб тривершинний граф співпав з частиною чотиривершинного. Виділена структура у добутку графів утворює два повних тривершинних графа, що мають спільні вершини та є двома рішеннями задачі. Але задача виділення повних підграфів (клік) також є NP-повною та при більшій кількості вершин графів так просто не розв'язується. При розробці NP-процесора на електронній чи іншій фізичній основі ми можемо або покласти на нього приведені вище перетворення, або виконати їх на звичайному комп'ютері, звівши початкову NP-задачу до NP-задачі пошуку повних підграфів у добутку графів. Оберемо перший варіант, він веде до більших апаратних витрат, але пристрій, що розв'язує NP-задачу пошуку повного підграфа буде окремим випадком реалізації пристрою, що розв'язує NP-задачу пошуку в графі частин, ізоморфних заданому графу. Проаналізуємо побудову добутку графів (Фіг. 4) і розміщення на ньому вершин повного підграфа - рішення. Візьмемо будь-яке одне із двох рішень. Основна властивість рішення - на кожному стовбці добутку графів повинно бути по одній вершині повного підграфа - рішення, на кожному рядку - не більш однієї. 1. Для NP-процесора знадобиться обчислювальне матричне середовище, що має чотири рядки по три елементи або у загальному випадку N рядків і К стовбців, де N більше або рівне К. Середовище допускає на кожному стовбці тільки один елемент у стаціонарному активному стані, а на кожному рядку не більше одного елемента в стаціонарному активному стані. NP-процесор (Фіг. 8) складається із обчислювального середовища 2, блока зчитування рішення 4, інтерференційного блока 3, призначеного для зберігання та інтерпретації умов задачі, блока динамічного вирівнювання активності елементів середовища 1, призначеного для контролю за реалізацією властивостей середовища за п. 1. Як обчислювальне середовище використаємо відомий NК-елементний матричний тригер (US Patent 3,764,919, Oct. 9, 1973 Filed: Dec. 22, 1972 Fig.9.). Там же описано його функціонування. Один з варіантів 43-елементного матричного тригера побудований на логічних елементах АБО-НI (NOR) і використовується нижче як приклад обчислювального середовища 2 (Фіг. 8) для NP-процесора. Обчислювальне середовище складається з множини багатоелементних тригерів, а саме з чотирьох трьохелементних тригерів і трьох чотирьохелементних тригерів поєднаних між собою через спільні елементи так, що установка в активний стан спільного елемента приводить до установки в неактивний стан всіх елементів багатоелементних тригерів, пов'язаних спільним елементом. Елементи багатоелементних тригерів мають по два забороняючих установку в активний стан входи. Додатково можуть бути введені входи для конфігурування і зв'язку з іншими пристроями. Запропоноване обчислювальне середовище, як і усі наведені нижче технічні рішення, по аналогії може бути розширене до практичних значень N і К. Розподіл стаціонарних активних станів по 43-елементному матричному тригеру, аналогічно розподілу вершин повного під графа в добутку графів (Фіг. 4), буде рішенням задачі, воно подається на блок зчитування рішення 4, котрий тут докладно не розглядається. Для рішення NP-задач на обчислювальному середовищі введемо залежні від умов задачі взаємоподавляючі (інтерференційні) зв'язки між елементами з різних стовбців обчислювального середовища. Зв'язки вводяться між тими елементами, для яких відповідні їм вершини добутку графів не зв'язані. Ця частина NP-процесора - інтерференційний блок 3, також має матричну (Фіг. 8) структуру 43 (у загальному випадку NК) і складається з 12 (NК) елементів. Одне з можливих схемотехнічних рішень nk-елемента інтерференційного блока 3 (Фіг. 8), де n-номер рядка, в котрому знаходиться елемент, a k-номер стовбця, представлено на Фіг. 7. Кожний nk-елемент використовує як вхідні дані для рішення NP-задачі n-тий рядок 25 (Фіг. 7) матриці суміжності чотири(N)вершинного графа і k-тий стовбець 27 (Фіг. 7) матриці суміжності три(К)вершинного графа. На вхід кожного nk-елемента інтерференційного блока подаються чотири (N) вихідних сигнали з чотирьох (N) елементів k-того стовбця обчислювального середовища. Елемент інтерференційного блока формує дві логічні АБО (OR), чи аналогові суми вихідних сигналів елементів з k-того стовбця обчислювального середовища. Суми формуються двома суматорами 13 і 14 (Фіг. 7). На суматорі 14 (Фіг. 7) формується сума (типу 0) з виходів 2 UA 111169 C2 5 10 15 20 25 30 35 40 45 50 55 60 елементів обчислювального середовища відповідним нулям в n-тому рядку матриці суміжності чотири(N)вершинного графа. На суматорі 13 (Фіг. 7) формується сума (типу 1) з виходів елементів обчислювального середовища відповідним одиницям в n-тому рядку матриці суміжності чотири(N)вершинного графа. Для цього, збережені в елементі блока значення n-того рядка 25 (Фіг. 7) матриці суміжності чотири(N)вершинного графа інвертуються інверторами 1, 2, 3, 4, (Фіг. 7), інверсні значення керують ключами 9, 10, 11, 12, (Фіг. 7), що пропускають сигнали з обчислювального середовища на суматор 14 (Фіг. 7). Прямі значення n-того рядка керують ключами 5, 6, 7, 8, (Фіг. 7), що пропускають сигнали з обчислювального середовища на суматор 13 (Фіг. 7). Керовані ключі можуть бути реалізовані на аналогових ключах або логічних ключах I (AND). У кожному із рядків елементів інтерференційного блока такі суми двох типів, що сформовані кожним елементом рядка, подаються на входи всіх елементів цього ж рядка інтерференційного блока (Фіг. 8). На суматорі 18, nk-того елемента інтерференційного блока (Фіг. 7), ці суми підсумовуються за типами та подаються на забороняючий вхід nk-того елемента обчислювального середовища. Тип сум (0-вого або 1-ого типу) визначається нулем або одиницею в k-тому стовбці 27 (Фіг. 7) матриці суміжності три(К)вершинного графа. Значення маски 26 (Фіг. 7) використовується для заборони обробки в елементі nk своїх сум, сформованих суматорами 13, 14 (Фіг. 7). Маска може застосовуватись для конфігурування NP-процecopa під розмірність NP-задачі. В результаті такої побудови схеми інтерференційний блок фізично реалізує математичну процедуру обчислення добутку графів. Для кожного чотирьохелементного тригера залежно від умов NP-задачі обчислюються аналогові або логічні суми величин активних станів підмножин його елементів. Будь-які з обчислених сум або неактивні сигнали залежно від умов задачі можуть бути подані на входи заборони установки в активний стан будь-якого елемента будьякого трьохелементного тригера, поєднаного з вищезгаданим чотирьохелементним тригером через спільний елемент. Конкретних варіантів схемо-технічної реалізації NP-процесора може бути безліч, наприклад, на позитивній і негативній логіці, аналоговій схемотехніці і т. д. II. Активність nk-того елемента обчислювального середовища блокується через його забороняючий вхід nk-тим елементом інтерференційного блока, якщо будь-який інший активний елемент обчислювального середовища, розташований на будь-якому іншому стовбці, не зв'язаний з ним у добутку графів (Фіг. 4). Розглянемо роботу інтерференційного блока на прикладі двох не зв'язаних в добутку графів вершин 32 і 13 (Фіг. 4). У відповідності з п. ІІ елементи обчислювального середовища 2 з індексами 3,2 і 1,3 (Фіг. 8) не можуть одночасно знаходитись в активному стані, а на виходах 13 однойменних елементів інтерференційного блока 3 (Фіг. 8) мають бути присутніми сигнали заборони переходу в активний стан для елементів 3,2 і 1,3 обчислювального середовища 2 (Фіг. 8). Якщо елемент 3,2 (на третьому рядку та другому стовбці) обчислювального середовища 2 (Фіг. 8) знаходиться в активному стані, тоді на виході 13 елемента 1,3 інтерференційного блока 3 (Фіг. 8) повинен бути сигнал заборони переходу в активний стан елемента 1,3 обчислювального середовища 2 (фіг. Ф). Покажемо це. Розглянемо роботу елемента інтерференційного блока (Фіг. 7). Для елемента 1,3 блока 3 (Фіг. 8) значеннями першого рядка матриці чотиривершинного графа 25 (Фіг. 7), маски 26 (Фіг. 7) і третього стовбця 27 (Фіг. 7) матриці суміжності тривершинного графа будуть бітові рядки "1110", "110", "001". Ці бітові рядки показано на умовному зображенні елемента 1.3 інтерференційного блока 3 (Фіг. 8). Вихідний сигнал елемента формує суматор 18 (Фіг. 7) і зв'язана з ним частина схеми. Активний сигнал на виході суматора можливий, тільки якщо хоча б на одному виході елементів 15, 16, 17, 19, 21, 23 присутній активний сигнал. Елементи 17 і 23 (Фіг. 7) можна виключити з подальшого аналізу, тому що вони заблоковані нулем у масці 26. Для установки в активний стан хоча б одного із елементів, що залишилися, 15, 16, 19, 21 (Фіг. 7) необхідно, щоб хоча б один із входів 6, 8 елемента 1,3 інтерференційного блока 3 (Фіг. 8) знаходився в активному стані. Вхід 6 елемента 1,3 блока 3 (Фіг. 8) у відповідності із схемою (Фіг. 8) зв'язаний з виходом 11 елемента 1,1 (Фіг. 8) інтерференційного блока 3. Елемент 1,1 (Фіг. 8) інтерференційного блока 3 приймає сигнал активності елемента 1,1 (Фіг. 8) обчислювального середовища 2 на свій вхід 1. Сигнал з цього входу надходить на ключ 5 всередині інтерференційного блока (Фіг. 7), відкритий першою одиницею у першому рядку "1110" матриці суміжності чотиривершинного графа, записаному в елемент 1,1 (Фіг. 8) інтерференційного блока 3. З виходу ключа 5 (Фіг. 7) сигнал надходить на вхід суматора 13 (Фіг. 7), з виходу 3 UA 111169 C2 5 10 15 20 25 30 35 40 45 50 55 60 суматора 13 на вихід 11 елемента 1,1 (Фіг. 8) інтерференційного блока 3. Таким чином, проходження сигналу блокування повністю доведено. Результатом роботи інтерференційного блока може бути і те, що будь-який один активний елемент, що не зв'язаний у добутку графів з іншими елементами, подавить активність інших. Таке ж може статись з будь-якою підмножиною взаємно зв'язаних активних елементів з кількістю вершин, меншою трьох (К), і це не буде рішенням NP-задачі. III. Рішенням NP-задачі, незалежно від її умов, може бути тільки три К) одночасно активних, взаємно не блокованих стани елементів, по одному в кожному стовбці обчислювального середовища. Для цього потрібно, щоб величина активності в кожному з трьох (К) стовбців обчислювального середовища в процесі динамічних змін, перехідних процесів, в обчислювальному середовищі була не вище, ніж в інших двох (К-1) стовбцях. Одночасний, однаковий ріст активності усіх трьох (К) елементів різних стовбців майже до стаціонарного стану, тобто рішення NP-задачі, досягається введенням від'ємних зворотних зв'язків між (К) стовбцями обчислювального середовища в блоці 1 (Фіг. 8) - динамічного вирівнювання активності. У двох варіантів виконання елементів 1,1, 1,2, 1,3 блока динамічного вирівнювання активності 1 (Фіг. 8), зображених на Фіг. 5, 6, суми активності всіх елементів спочатку формуються аналоговими або логічними "АБО" (OR) суматорами 1 (Фіг. 5, 6) для кожного стовбця обчислювального середовища окремо. Виходить три (К) суми, величина котрих відбиває динамічну активність стовбців обчислювального середовища. Потім для кожного стовбця обчислюються аналоговими компараторами або логічними компараторами 2 та 3 (Фіг. 5, 6) величини перевищень його активності над активністю інших стовбців. Такі перевищення складаються аналоговим або логічним суматором 4 (Фіг. 5, 6). В результаті для кожного стовбця обчислювального середовища, а отже для кожного чотирьохелементного тригера, отримується сума перевищень його активності над активністю інших стовбців, тобто інших чотирьохелементних тригерів. Чотирьохелементні тригери складають підмножину всіх багатоелементних тригерів, з яких складається обчислювальне середовище. Динамічна активність кожного стовбця обчислювального середовища, що має не нульову суму перевищень над активністю інших стовбців, повинна бути подавлена у відповідності з п. ІІІ. Подавлення активності у першому варіанті реалізовано поданням значення суми перевищень на усі забороняючі входи стовбця обчислювального середовища (Фіг. 6). У другому варіанті (Фіг. 5), величина, що подається на забороняючий вхід кожного елемента стовбця обчислювального середовища, індивідуальна і залежить від величини його активності. Для цього кожний елемент кожного стовбця обчислювального середовища охоплюється, керованим за інтенсивністю, від'ємним зворотним зв'язком. Сигнал зворотного зв'язку подається з виходу елемента обчислювального середовища на його забороняючий вхід через елемент блока динамічного вирівнювання активності. Цей сигнал зворотного зв'язку в елементі блока динамічного вирівнювання активності (Фіг. 5) пропускається через аналогові ключі або керовані підсилювачі, або логічні ключі "І" (AND) 5, 6, 7, 8. На входи керування інтенсивністю від'ємного зворотного зв'язку елементів 5, 6, 7, 8 (Фіг. 5) подається величина суми перевищень. Чим більша сума перевищень, тим більш інтенсивність від'ємного зворотного зв'язку. NP-процесор (Фіг. 8) працює наступним чином. Зміна вхідних даних, розмішених в інтерференційному блоці 3, призводить до розладу всередині поточного розподілу активних станів у обчислювальному середовищі 2. Структура інтерференційних зв'язків змінилась, частина активних станів обчислювального середовища подавляється новими інтерференційними зв'язками до неактивного стану. Інші активні стани вирівнюються до неактивного стану блоком динамічного вирівнювання активності 1. Усі елементи обчислювального середовища 2 переходять у близькі до неактивних стани. Цей стан обчислювального середовища є нестійким, як і перехідний стан звичайного двійкового тригера. Оскільки всі елементи обчислювального середовища 2 охоплено позитивними зворотними зв'язками, починається процес хаотичного зростання активності елементів обчислювального середовища. Але ріст активності будь-якого елемента обчислювального середовища обмежено взаємними забороняючими зв'язками за умовами п. І та інтерференційними зв'язками за п. ІІ, Якщо у процесі зростання активності, активність елемента якогось стовбця перевищить величину активності елемента у іншому стовбці, то вона буде подавлена від'ємними зворотними зв'язками у відповідності з п. III. Усі наведені вище процеси відбуваються одночасно. Взаємодія таких процесів призводить до коливань, у яких беруть участь різні комбінації елементів обчислювального середовища. Кількість таких комбінацій (форм коливань) як "віртуальних машин" зростає експоненційно з ростом кількості елементів обчислювального середовища. Умови за п. ІІ та п. III приводять до їх взаємного подавлення, інтерференції. 4 UA 111169 C2 5 Досягти максимальній активності може тільки така форма коливань, котра має узгоджений, рівномірний ріст активності, контрольований блоком 1 динамічного вирівнювання активності. Розподіл максимальної стаціонарної активності по елементам обчислювального середовища буде рішенням NP-задачі. Рішення зчитується пристроєм зчитування рішення 4. Будь-яка зміна у вхідних даних приведе із-за дії від'ємних зворотних зв'язків у блоці динамічного вирівнювання активності 1 та інтерференційному блоці 3 до нового коливального процесу в обчислювальному середовищі 2 та нового рішення. Якщо рішення NP-задачі не існує, процес коливань буде продовжуватись без кінця або до вводу даних, що приведуть до рішення. 10 ФОРМУЛА ВИНАХОДУ 1. Спосіб роботи NP-процесора, який складається з кінцевої множини багатоелементних тригерів, які мають входи установки в активний стан або входи заборони установки в активний стан, який відрізняється тим, що для кожного багатоелементного тригера обчислюють суми величини активних станів підмножин його елементів за допомогою аналогового або логічного суматора, обчислені суми або неактивні сигнали подають на входи заборони установки в активний стан або входи установки в активний стан будь-якого елемента будь-якого багатоелементного тригера, додатково вводять керовані від'ємні зворотні зв'язки для кожного елемента кожного багатоелементного тригера, інтенсивність від'ємного зворотного зв'язку для всіх елементів будь-якого багатоелементного тригера визначають у вигляді аналогової або логічної суми перевищень його суми величин активних станів всіх елементів над аналогічними сумами інших багатоелементних тригерів, перевищення обчислюють за допомогою аналогових або логічними компараторів, суму перевищень визначають за допомогою аналогового або логічного суматора. 2. Спосіб роботи NP-процесора, який складається з кінцевої множини багатоелементних тригерів, які мають входи установки в активний стан або входи заборони установки в активний стан, який відрізняється тим, що для кожного багатоелементного тригера обчислюють суми величини активних станів підмножин його елементів за допомогою аналогового або логічного суматора, обчислені суми або неактивні сигнали подають на входи заборони установки в активний стан або входи установки в активний стан будь-якого елемента будь-якого багатоелементного тригера, на входи заборони установки в активний стан всіх елементів кожного багатоелементного тригера подають аналогову або логічну суму перевищень його суми величин активних станів всіх елементів над аналогічними сумами інших багатоелементних тригерів, перевищення обчислюють аналоговими або логічними компараторами, суму перевищень визначають аналоговим або логічним суматором. 3. Спосіб роботи NP-процесора, який складається з кінцевої множини багатоелементних тригерів, поєднаних між собою через спільні елементи так, що установка в активний стан спільного елемента приводить до установки в неактивний стан всіх елементів багатоелементних тригерів, поєднаних спільним елементом, елементи багатоелементних тригерів мають входи установки в активний стан або входи заборони установки в активний стан, який відрізняється тим, що для кожного багатоелементного тригера з підмножини багатоелементних тригерів обчислюють суми величини активних станів підмножин його елементів за допомогою аналогового або логічного суматора, обчислені суми або неактивні сигнали подають на входи заборони установки в активний стан або входи установки в активний стан будь-якого елемента будь-якого багатоелементного тригера, поєднаного з вищезгаданим багатоелементним тригером через спільний елемент, вводять керовані від'ємні зворотні зв'язки для кожного елемента кожного багатоелементного тригера з підмножини багатоелементних тригерів, інтенсивність від'ємного зворотного зв'язку для всіх елементів будь-якого багатоелементного тригера з підмножини багатоелементних тригерів визначають у вигляді аналогової або логічної суми перевищень його суми величин активних станів всіх елементів над аналогічними сумами інших багатоелементних тригерів, перевищення обчислюють за допомогою аналогових або логічних компараторів, суму перевищень визначають за допомогою аналогового або логічного суматора. 4. Спосіб роботи NP-процесора, який складається з кінцевої множини багатоелементних тригерів, поєднаних між собою через спільні елементи так, що установка в активний стан спільного елемента приводить до установки в неактивний стан всіх елементів багатоелементних тригерів, поєднаних спільним елементом, елементи багатоелементних тригерів мають входи установки в активний стан або входи заборони установки в активний стан, який відрізняється тим, що для кожного багатоелементного тригера з підмножини 5 UA 111169 C2 багатоелементних тригерів обчислюють суми величини активних станів підмножин його елементів за допомогою аналогового або логічного суматора, обчислені суми або неактивні сигнали подають на входи заборони установки в активний стан або входи установки в активний стан будь-якого елемента будь-якого багатоелементного тригера, поєднаного з вищезгаданим багатоелементним тригером через спільний елемент, на входи заборони установки в активний стан всіх елементів кожного багатоелементного тригера з підмножини багатоелементних тригерів подають аналогову або логічну суму перевищень його суми величин активних станів всіх елементів над аналогічними сумами інших багатоелементних тригерів, перевищення обчислюють за допомогою аналогових або логічних компараторів, суму перевищень визначають за допомогою аналогового або логічного суматора. 6 UA 111169 C2 7 UA 111169 C2 8 UA 111169 C2 9 UA 111169 C2 Комп’ютерна верстка О. Гергіль Державна служба інтелектуальної власності України, вул. Василя Липківського, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут інтелектуальної власності”, вул. Глазунова, 1, м. Київ – 42, 01601 10