Кліть гвинтова тривалкова планетарна консольна обтискна
Номер патенту: 99867
Опубліковано: 10.10.2012
Автори: Литвинов Віктор Іванович, Жукова Наталя Вікторівна, Литвинова Таїсія Серафімівна
Формула / Реферат
Кліть гвинтова тривалкова планетарна консольна обтискна, що містить розміщений у нерухомому корпусі механізм приводу кліті з центральним колесом і ротором, механізм валків зі своїм корпусом, поміщений у ротор кліті та зчленований з центральним колесом, при цьому осі робочих валків схрещуються з віссю прокатки під кутом ![]() і зміщені перпендикулярно осі прокатки на найкоротшу відстань
і зміщені перпендикулярно осі прокатки на найкоротшу відстань ![]() , а самі валки мають радіус
, а самі валки мають радіус ![]() , довжину
, довжину ![]() і відповідну їм зону деформації з радіусом
і відповідну їм зону деформації з радіусом ![]() , довжиною
, довжиною ![]() , обмежені кутом валка
, обмежені кутом валка ![]() і відповідно кутом зони деформації
і відповідно кутом зони деформації ![]() , яка відрізняється тим, що механізм валків установлений так, що кут схрещування осей валків і прокатки становить
, яка відрізняється тим, що механізм валків установлений так, що кут схрещування осей валків і прокатки становить ![]() , кут зони деформації
, кут зони деформації ![]() , відповідно кут валка
, відповідно кут валка ![]() , при цьому центральне колесо кліті встановлено з можливістю обертання відносно ротора з початковою кутовою швидкістю
, при цьому центральне колесо кліті встановлено з можливістю обертання відносно ротора з початковою кутовою швидкістю ![]() , а до приводу ротора або центрального колеса, відповідно при парній або непарній кількості ступенів передач валкового механізму, з'єднаний зовнішній редуктор з коефіцієнтом механічної передачі
, а до приводу ротора або центрального колеса, відповідно при парній або непарній кількості ступенів передач валкового механізму, з'єднаний зовнішній редуктор з коефіцієнтом механічної передачі 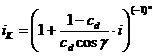 ,
,
де ![]() ,
, ![]() - радіуси підкату і розкату;
- радіуси підкату і розкату;
![]() ;
;
![]() - вісь валка, координати точок якої відлічуються від найкоротшої відстані
- вісь валка, координати точок якої відлічуються від найкоротшої відстані ![]() ;
;
![]() - вісь прокатки, координати точок якої відлічуються від найкоротшої відстані
- вісь прокатки, координати точок якої відлічуються від найкоротшої відстані ![]() ;
;
![]() - сумарний коефіцієнт передачі валкового механізму,
- сумарний коефіцієнт передачі валкового механізму, ![]() - кількість ступенів передач цього механізму;
- кількість ступенів передач цього механізму;
![]() - коефіцієнт передачі обертання валка
- коефіцієнт передачі обертання валка ![]() і металу
і металу ![]() ;
;
![]() - кутова швидкість обертання центрального колеса;
- кутова швидкість обертання центрального колеса;
![]() - кутова швидкість обертання ротора, рівна зі зворотним знаком кутовій швидкості обертання металу
- кутова швидкість обертання ротора, рівна зі зворотним знаком кутовій швидкості обертання металу ![]() при нерухомому роторі кліті;
при нерухомому роторі кліті;
![]() - початкова кутова швидкість валка при заданій швидкості
- початкова кутова швидкість валка при заданій швидкості ![]() входу заготовки в кліть.
входу заготовки в кліть.
Текст
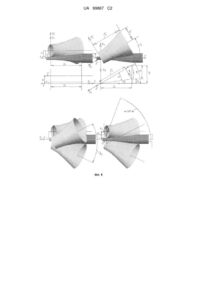
Реферат: Винахід належить до прокатного виробництва і може бути використаний на безперервних прокатних станах. Кліть містить розміщений у нерухомому корпусі механізм приводу кліті з центральним колесом і ротором та механізм валків зі своїм корпусом, поміщений у ротор кліті та зчленований з центральним колесом. Осі робочих валків схрещуються з віссю прокатки під кутом 30 і зміщені перпендикулярно осі прокатки. Валки мають певний змінний радіус та довжину і відповідну їм зону деформації, обмежену кутом зони деформації та кутом валка. При цьому швидкість ротора знаходиться у визначеному початковому співвідношенні до швидкості центрального колеса, а до приводу ротора або центрального колеса, відповідно при парній або непарній кількості ступенів передач валкового механізму, з'єднаний зовнішній редуктор для вирівнювання швидкостей електродвигунів кліті. Прокатка в такій кліті, де радіуси валків по всій своїй довжині пропорційно більше радіуса зони деформації у відношенні 4:1, забезпечує мінімальний знос валків. Деформація металу відбувається без його обертання і скручування з великою витяжкою, малими енерговитратами та з максимальною продуктивністю. UA 99867 C2 (12) UA 99867 C2 UA 99867 C2 5 10 15 Винахід належить до прокатного виробництва і може бути використаний на безперервних прокатних станах. Дві такі кліті можуть замінити 15…17 чорнових клітей подовжньої прокатки із сумарною-витяжкою близько 100 одиниць, що значно заощадить обладнання і споживану енергію при виробництві сортового прокату. Найбільш близьким аналогом до технічного рішення, що заявляється, є кліть тривалкова гвинтова консольна планетарна (Патент України № 88522, кл. В21В 13/12. опубл. Бюл. № 20, 2009 p.). Ця кліть містить механізм приводу кліті з обертовим ротором і центральним колесом, механізм валковий із своїм корпусом, розташований у роторі, і нерухомий корпус кліті. У цій кліті зафіксовані характерні параметри гвинтової прокатки: найкоротша відстань d і кут схрещування між осями прокатки і валка. Дана кліть є найбільш близькою по технічній суті до кліті, яка заявляється, тому що розробка її конструкції заснована на простих функціональних зв'язках характерних параметрів гвинтової прокатки з геометрією валків і зони деформації, які використовуються в подальшій оптимізації об'єкта і тому ця кліть вибрана як прототип. Загальними ознаками для кліті, що заявляється, і кліті, вибраної як найближчий аналог, є: механізм приводу кліті із центральним колесом і ротором, механізм валків із своїм корпусом, поміщений у ротор кліті, і нерухомий корпус кліті, валки робочі, осі яких схрещуються стосовно осі прокатки під кутом і зміщені перпендикулярно осі прокатки на найкоротшу відстань r cos і відповідну їм d 1 , валки мають радіус r ' z' c 2 d2 z' 2 tg 2 і довжину z '0 z 0 d 1 c d cos зону деформації з радіусом r z 20 валка sin MAX розкату, c d 25 30 35 40 2 r1 z 2 tg 2 3 sin і відповідно кутом зони MIN MAX , де r0; r1 - радіуси підкату і 2 2 3 cos 2 1 3 cos 2 , z' - вісь валка, координати точок якої відлічуються від найкоротшої відстані d , z - вісь прокатки, координати точок якої відлічуються від найкоротшої відстані d. Стосовно прототипу тут формули приймають більш простий вид, якщо прийняти =с, =(1с), =+. Недолік відомої кліті в тому, що в даній конструкції кут схрещування між осями прокатки і валка вибраний більшим (45). Такий же кут і в інших відомих конструкціях кліті (Черные металлы, № 22, 1973 р…, с. 29…35; Черные металлы, №1, 1988 р., с. 26…32). При таких кутах схрещування валки мають малий радіус на своїй калібруючій ділянці, що призводить їх до швидкого зносу, що у виробничих умовах не економно. В основу винаходу поставлена задача - удосконалити кліть гвинтову тривалкову планетарну консольну обтискну, яка забезпечить раціональну технологію гвинтової прокатки, за рахунок вибору оптимального кута схрещування між осями прокатки і валка , а також геометрії зони деформації і валка і кінематичних параметрів кліті. Це дозволить збільшити розміри валків на калібруючій ділянці, збільшити швидкість прокатки, вести обтискний процес без обертання і скручування металу з великими витяжками і малими енерговитратами, а також зменшити питомий знос валків на тонну прокату. Поставлена задача вирішується тим, що у гвинтовій тривалковій планетарній консольній обтискній кліті, що містить механізм привода кліті із центральним колесом і ротором, механізм валків із своїм корпусом, поміщений у ротор кліті, і нерухомий корпус кліті, валки робочі, осі яких схрещуються стосовно осі прокатки під кутом і зміщені перпендикулярно осі прокатки на r найкоротшу відстань d 1 , валки мають радіус r ' z' c 2 d2 z' 2 tg 2 і довжину d 1 c d z '0 z 0 cos cos відповідна їм зона деформації з радіусом r z r 2 z 2 tg 2 1 і довжиною 2 2 r0 r1 , обмежені кутом валка sin MAX 3 sin і відповідно кутом зони tg 2 MIN MAX , відповідно до винаходу, механізм валків установлений так, що кут z0 45 і довжиною z 0 2 2 r0 r1 , обмежені кутом tg 1 UA 99867 C2 схрещування осей прокатки і валка становить 30 , кут зони деформації arctg1 c d tg30 , відповідно кут валка 30 arctg1 c d tg30 , при цьому центральне колесо кліті стосовно ротора обертається з початковою кутовою швидкістю Ц Р 1 і ім , а 5 до приводу ротора або центрального колеса відповідно при парній або непарній кількості ступенів передач валкового механізму з'єднано зовнішній редуктор з коефіцієнтом механічної ( 1)n 1 c d передачі iK 1 , де c d cos i 1n i1 i2...in - сумарний коефіцієнт передачі валкового механізму, n - кількість щаблів передач цього механізму; 1 cd ' - коефіцієнт передачі обертання валка ' і металу M ; iM M c d cos 10 15 20 25 30 35 40 45 Ц - кутова швидкість обертання центрального колеса; P - кутова швидкість обертання ротора, рівна зі зворотним знаком кутової швидкості обертання металу P M при нерухомому роторі кліті; V0 початкова кутова швидкість валка при заданій швидкості V0 входу заготовки ' d c d sin в кліть. Характерні і основні параметри гвинтової прокатки, а також кінематичні схеми гвинтової планетарної кліті, що пояснюють вибір заявлених нових ознак винаходу, наведені на фіг. 1…6. На фіг. 1 - Характерні і основні параметри гвинтової прокатки; На фіг. 2 - Граничні умови (d0, =0); (d=0, 0), при яких гвинтова прокатка неможлива; На фіг. 3 - Кінематична схема планетарної гвинтової кліті із двоступінчастим валковим механізмом і головною конічною передачею; На фіг. 4 - Кінематична схема планетарної гвинтової кліті з одноступінчастим валковим механізмом і головною гепоїдною передачею; На фіг. 5 - Максимальні валки для кліті з кутом схрещування =45°(верхні), а також валки для кліті з кутом =30°(нижні) при дотриманні умови не скручування металу; На фіг. 6 - Валки для клітей з кутом схрещування =45°(верхні), а також валки для кліті з кутом =30° (нижні) при дотриманні умови не скручування металу. Виходячи із суті винаходу, що ґрунтується на аналізі геометрії гвинтової прокатки, об'єктивно виходить так, що три валки кліті, які розташовуються в обмеженому валковому просторі, жорстко зв'язують між собою складним нелінійним чином незалежні характерні геометричні параметри гвинтової прокатки d i (найкоротша відстань між осями прокатки і валка і кут схрещування між цими осями). У цій складній трансцендентній нелінійній геометрії гвинтової прокатки (див. Проектирование профилировок валков клетей винтовой прокатки /Ф.Е. Долженков, А.Ю. Литвиненко, В.І. Литвинов, Ф.А. Писаренко. - К.: Техника, 1992. - 135 с.) за допомогою простих геометричних моделей вдалося знайти цей зв'язок у вигляді простих функцій. Вони дозволяють вибрати оптимальні d і . Оптимізація гвинтової прокатки в планетарному виконанні ґрунтується на простих вимогах: 1. Вихідними даними для побудови кліті є задані радіуси підкату r0 і розкату r1. Цієї інформації достатньо, щоб побудувати в першу чергу геометрію валків і зони деформації. Валки тут представляються у вигляді заготовок - гіперболоїдів, які надалі здобувають захоплюючі, деформуючі і калібруючі ділянки. Основні елементи кліті, які досить відомі, добудовуються до інструмента з вимогою їх неперетинання з аксіально-симетричними сусідами. Вони не повинні заходити за межі продовженого максимального гіперболоїда валка. Маючи початкову інформацію з геометрії в простому аналітичному вигляді, кінематика і динаміка технологічного процесу також представляється в простій аналітичній формі. Отже, оптимізація кліті практично залежить від геометрії гвинтової прокатки. 2. Валки повинні мати розміри як мінімум в 3-4 рази більше стосовно металу, який деформується, що в існуючих тривалкових планетарних клітях не дотримується. Початкові діаметри валка досить великі, а калібруюча ділянка інструмента має малий діаметр, тому ця ділянка швидко зношується, що в умовах виробництва приносить додаткові витрати. 2 UA 99867 C2 3. Обтискна планетарна гвинтова кліть повинна мати максимальну поздовжню швидкість прокатки VZ стосовно аксіальної швидкості V заготовки, яка обертається щодо ротора кліті. V Даний критерій гвинтової прокатки КВП Z відповідає максимальному ККД кліті. V 5 10 15 20 25 30 35 4. У звичайних гвинтових клітях існує ефект скручування металу. У тій кліті, де прокатка відбувається за найкоротшою відстанню d, від скручування металу позбутися принципово неможливо. Що стосується планетарної кліті, то згаданий ефект не повинен мати місце, тому що частково втрачається її перевага стосовно звичайної прокатки, якщо підкат або розкат починає повільно обертатися відносно один до одного. Усунення цього ефекту потребує додаткових витрат енергії при втриманні підкату в аксіальному напрямку, якщо аксіальна швидкість розкату підтримується на нулі приводом ротора кліті. 5. Для побудови приводу робочих валків і приводу ротора кліті необхідна інформація про початкове співвідношення кутових швидкостей центрального колеса Ц і ротора Р. Зрозуміло, що умова азимутального спокою розкату залежить не тільки від параметрів механічної передачі кліті, але і від характерних геометричних її параметрів, що необхідно виявити. З метою подальшої оптимізації параметрів планетарної гвинтової кліті, які використовуються в пропонованій модернізації обладнання, запишемо в більш компактній формі відомі основні аналітичні залежності дотичних поверхонь обертання валка і "фіктивної" зони деформації, далі вона буде називатися "зона". Отже, між осями прокатки z і валка z' кут схрещування рівний і ці осі відстоять один від одного на найкоротшій відстані d. Як і в прототипі, зазначені поверхні обертання валка і "зони" є гіперболоїдами, отриманими обертанням однієї й тієї ж прямої лінії. Ця твірна пряма відстоїть від осі прокатки на відстані, рівній заданому радіусу розкату r 1, і має з віссю прокатки кут схрещування , так званий кут "зони" . "Зона" - гіперболоїд утворюється обертанням твірної прямої лінії навколо осі прокатки z, а валок - гіперболоїд – обертанням тієї ж прямої лінії навколо осі валка z'. Між твірною прямою і віссю валка кут схрещування рівний =-, так званий кут валка . Нижні індекси "0", "1" відповідають початку і кінцю "зони" або валка; верхній індекс, штрих, «/» присвоюється величинам, відповідним до осі валка; Х і, X i' , і=1,2,3 координати, пов'язані з віссю прокатки і віссю валка. Валок, "зона" і використані характерні і основні параметри гвинтової прокатки показані на фіг. 1. Виходи валка і зони сполучені з найкоротшою відстанню d. При такій конфігурації найкоротша відстань d стає максимально можливою у тривалковій системі з максимальними розмірами валків. Якщо "зона" буде зміщена уздовж осі прокатки від свого оптимального положення, валки повинні бути збільшені, але вони будуть перетинатися, тоді d треба зменшувати, але це призводить до зменшення ККД гвинтової кліті. Отже, таке положення "зони" на осі прокатки відповідає оптимальній геометрії системи валки - метал. Основні робочі формули, виходячи із заданих радіусів підкату r 0 і розкату r1, мають простий вигляд: AB d 0 d 2 3 cos X1A d; X2 A d 40 - найкоротша відстань між осями валків; 1 3 cos 2 3 sin2 2 1 3 cos ; X3 A d 3 sin cos 1 3 cos2 . 2 cos2 sin2 3 1 cos2 ; X d ; X d 3 sin cos . X1B d 2B 3B 2 2 1 3 cos 1 3 cos 1 3 cos2 3 cos ; 1 3 cos 2 AB AB sin 2 cos 2 1 1 3 cos 2 cos 1 3 cos 2 ; sin ; 90 ; ; cos 2 2 1 3 cos 1 3 cos sin 2 2 cos 4 cos ; cos ; 1 3 cos 2 1 3 cos 2 3 UA 99867 C2 d ' r1 0 cos d 2 сd cd 2 3 cos 2 1 3 cos 2 0 3 cos 2 cos 1 3 cos 2 d 1 3 cos 2 ' ' ; r1 c d d; d r1 r1; d 2 3 cos 2 1 3 cos 2 d проекц . 0 на пл. перпенд . осі прокатки 2 r1 ; 1 c d 3 2 3 ' 3 ;d r ; r' d ; r1 r1 ; 0 1 2 3 1 0 2 2 0 2 3 r ' z' c 2d2 z'2 tg2 - функція валка; d 5 ' cd r1 1 3 cos 2 2 3 cos 2 ' ; d r1 ; r1 r1 ; r1 1 c d 1 2 3 3 cos 2 1 2 3 3 cos 2 MAX; sin MAX 3 sin - максимальний кут валка; 2 2 r z r1 z 2 tg 2 - функція "зони"; MIN; MIN MAX - мінімальний кут "зони"; z0 10 2 2 r0 r1 2 cos ' ; z'0 z0 ; r0 z'0 tg2 c 2d2 ; d tg cos ' ' Тут z 0 - довжина "зони", z '0 - довжина валка, r0 , r1 - початковий і кінцевий радіуси валка. Точки z, z' - відлічуються на осях прокатки і валка від найкоротшої відстані d. Максимальні 3 sin і габарити валка визначаються максимальним кутом валка MAX arcsin 2 найкоротшою відстанню d r1 15 20 25 30 1 3 cos 2 1 2 3 3 cos 2 , мають простий вигляд і зручні при побудові кліті. У зв'язку з тим, що незалежний параметр d став залежним від кута і при його збільшенні d зменшується, об'єктивно існує оптимум вибору кута . Наведені функції задовольняють граничним умовам гвинтової прокатки, при яких сам процес прокатки неможливий. На фіг. 2 показані "валки", які перетворюються в конуси при d=0, 0. Ці конуси стикаються за максимальним кутом конуса MAX 0 . 0 - кут між осями 2 1 cos 0 3 3 sin 2 ; sin 0 . Тому sin MAX sin . В іншому 2 2 2 2 прикордонному випадку при d0, =0 "валки" перетворюються в циліндри, відповідні до формул, наведених вище. При росту кута схрещування циліндри перетворюються в гіперболоїди з таким же максимальним кутом валка МАХ. Якщо обертання валка ініціює рух і деформацію металу, тоді кінематика точок поверхні валка, що контактують із металом, має першорядне значення у виборі параметрів конструкції кліті. Відомо, що геометричне місце точок (ГМТ) валка, що мінімально відстоять від осі прокатки, визначає не тільки геометрію переходу металу від заготовки до кінцевого прокату, але і співвідношення поздовжньої і азимутальної течії металу. Для валка - гіперболоїда це ГМТ є не що інше, як вищезгадана пряма лінія, що утворює гіперболічні поверхні валка і "зони". В основній і штрихованій системах координат, пов'язаних з віссю прокатки z і віссю валків z', лінійні швидкості точок даної прямої при кутовій швидкості валка ', мають вигляд: сусідніх конусів, cos 0 1 ' ' V1 ' z' tg; V2 ' c1d; ' ' V1 V1; V2 V2 cos ; z' tg z cos sin tg z zc 2 sin ; cos cos 4 UA 99867 C2 r' a c1 1 ; c 2 ; d g 2 2 V V1 V2 ; V ' c1 cos 2 d2 z 2 c 2 sin 2 ; 2 V ' cos c1 d2 c 2z2tg2 ; 2 ' Vz V2 sin ; Vz ' c1d sin ; r' c d a V d tg ; c1 c 2; 1 d c d ; KВП1 z ; d d g V 2 c1 d2 c 2z2tg2 d2 z2tg2 2 Співвідношення поздовжньої і азимутальної швидкостей названих точок, що дуже важливо, не залежить від функції валка і "зони", воно є функцією характерних параметрів d, і координати z осі прокатки. Тому має сенс користуватися середнім критерієм КВП1 уздовж осі прокатки. dtg dtg z 1 z ; zОТН ; w ; ZОТН 0 ; d tg d 2tg2 d2 2 z 1 z dtg d tg2 10 Vz V c1 d tg K ВПср 5 1 Zоот Z ОТН 0 z ОТН 2 z ОТН w 2 Zоот 2 2 In z ОТН z ОТН w Z ОТН 0 1 2 1 z0 z 0 tg d Vz 1 d КВПср1 ln z0 1 V CP d tg 15 1 Z ОТН In 2 Z ОТН z ОТН w 2 ; w 2 . Другий критерій гвинтової прокатки характеризує скручування металу у зоні деформації. Скручування металу буде відсутнє, якщо співвідношення кутових швидкостей дотичних точок поверхонь валка і "зони" буде величиною постійною уздовж осі прокатки, тобто це співвідношення є функцією незалежних геометричних параметрів. 2 2 V r z r1 z2tg2 1 c d 2 d2 z2tg2 V ' cos c1 d2 c 2z2tg2 ; ; 2 2 2 2 2 2 cd cos c1 d c 2z tg ; при c 1 c 2 c d ; tg 1 c d tg; cos ; ' ' 1 c d 2 2 2 2 1 cd d z tg cd cos при обов'язковій умові tg 1 c d tg . ' 1 c d Третій критерій гвинтової прокатки стосується до її планетарного виконання (дивися кінематичні схеми на фіг. 3, 4). Планетарна гвинтова кліть, яка має два незалежні приводи валків і їх рухомого корпусу ротора кліті, належить до планетарних диференціальних механізмів із двома ступенями свободи. За допомогою даного планетарного механізму реалізується гвинтова прокатка без обертання металу навколо осі прокатки. Це головна відмінність даного обладнання дозволяє сполучити в безперервному режимі гвинтову і поздовжню прокатки металу. Кінематика такого складного об'єкта аналізується методом Вілліса. Суть цього методу полягає у відомості задачі аналізу планетарних і диференціальних механізмів до аналізу звичайних зубчастих передач шляхом переходу від абсолютного руху ланок розглянутого планетарного механізму до їхнього відносного руху стосовно водила. Тут водило називається ротором. Розрахунки планетарних і диференціальних передач можна робити, повідомивши подумки всьому механізму обертання з кутовою швидкістю, рівною за модулем і протилежною за напрямком кутової швидкості ротора (метод зупинки або метод Вілліса). KВП2 20 25 30 5 UA 99867 C2 5 10 15 20 25 30 35 40 У задачі для планетарної диференціальної гвинтової кліті застосуємо формулу Вілліса до центрального колеса (ц), ротора (р) і деформованого металу (м). Як зрозуміло з кінематичної схеми (фіг. 3) формула Вілліса має вигляд: Ц Р іМ і 2 і1 і . М Р Тут іМ, і2, і1, відповідно співвідношення між кутовими швидкостями валка і металу, між кутовими швидкостями шестірень валка і сателіта і кутовими швидкостями шестірень сателіта і центрального колеса. Тоді із цього виразу кутова швидкість металу буде у вигляді: Ц Р 1 і Р М . і Зрозуміло, що метал не буде обертатися при дотриманні кінематичної рівності: 1 i Ц 0, Р . Ц Р 1 іМ і2 і1 Це головне кінематичне співвідношення можна одержати із простих логічних розумінь. Коли ротор спочиває, відношення кутових швидкостей металу і центрального колеса буде у вигляді: Ц = -іМі2і1М при Р=0. Далі, щоб метал не обертався, необхідно ротор обертати з кутовою швидкістю, рівною кутовій швидкості металу, але зі зворотним знаком, тобто Р=-М. Тоді, щоб не змінився відносний рух центрального колеса і сателіта і їх вибране кінематичне співвідношення Ц = іМі2і1М = іМі2і1Р, центральну шестірню необхідно обертати з додатковою кутовою швидкістю Р. Тобто, сумарна кутова швидкість центральної шестірні приймає вид: Ц = іМі2і1Р+Р, ' 1 Ц Р 1 іМ і2 і1; іМ ; і і1і2.. М КВП2 В результаті отриманий той же результат у головному кінематичному співвідношенні планетарної гвинтової кліті, яке визначає умову відсутності обертання металу навколо осі прокатки. Коли ця умова отримана з різних точок зору, тоді вона вірна і її можна застосовувати при реалізації проекту розглянутої кліті. Отже, третій критерій гвинтової прокатки має вигляд: Ц Ц ' 1 сd КВП3 1 і; КВП3 1 і. Р М Р c d cos n Необхідно відзначити, що знак коефіцієнта передачі і=(-1 )·i1…in залежить від кількості ступенів передач механізму кліті. При використанні гіпоїдної одноступінчастої передачі (дивися фіг. 4) коефіцієнт i буде зі знаком (-). Знайдений третій критерій надійно можна використовувати в розрахунках коефіцієнтів механічної передачі приводу і є тільки початковою умовою для керування подвійним електроприводом планетарної гвинтової кліті. Динаміка процесу зажадає вести керування даним електроприводом зі зворотним зв'язком від датчика аксіальної швидкості розкату, але із зазначеною кінематичною початковою умовою. Так само третій критерій використовується при вирівнюванні обертів двигунів центрального колеса і ротора, що дуже зручно при регулюванні цих двигунів. На кінематичній схемі кліті (фіг. 3) установлено зовнішній редуктор приводу ротора з коефіцієнтом передачі, рівним 1 c d iK 1 i за умови рівності діаметрів коліс ротора і центрального колеса. На фіг. 4 c d cos показана кліть із одноступінчастою гіпоїдною передачею валкового механізму, тому зовнішній 1 cd редуктор з передаточним числом iK 1 c d cos колеса. 6 1 з'єднано із приводом центрального UA 99867 C2 5 10 15 20 25 30 Для виявлення оптимальних параметрів кліті з вихідними даними r 0=75 мм, r1=25 мм, виконана таблиця 1 з параметрами кліті: ' 2.25 рад с ' ' z , c d, d, r1, MAX, MIN, , z0, z'0, r0, 0 , KВПср1, Vz. d ' ,r ' , z0 У таблиці 1 параметри z 0 , z 0 0 відповідають двом парам кутів , =- при відсутності d скручування металу, а також за максимальним валком і мінімальною "зоною" MAX, MIN=-MAX. На фіг. 5 побудовані максимальні валки для кліті з кутом схрещування =45, a також валки для кліті з кутом =30 при дотриманні умови не скручування металу. При =30° кут "зони" і кут валка відрізняються від свого мінімального (=-МИН=2) і відповідно максимального значення (=МАХ-=2) на малу величину, при збільшеній довжині "зони" усього на 9 % стосовно "зони" кліті з кутом =45. Зрозуміло, що кут схрещування між осями прокатки і валка =30 більш підходить для виробництва прокату з погляду зносу інструменту. Тут валки і "зона" по всій своїй довжині мають пропорційні розміри у відношенні приблизно 4:1, що не спостерігається для кліті з кутом схрещування =45°. На фіг. 6 побудовані валки при відсутності скручування металу для тих же клітей з кутами схрещування =30°,45°. При =45° валки дуже поменшали, тому що кут "зони" і кут валка відрізняються від свого мінімального (=-МИН=10) і відповідно максимального значення (=МАХ-=10°) на більшу величину. Тому, у виробничих умовах, якщо дотримувати умови не скручування металу, кліть із кутом схрещування =45° застосовувати не можна. З наведених таблиць видно, що для кутів =30 і =46° критерій КВП1, що визначає ККД прокатки, однаковий, хоча він має максимум при =37°. Швидкість прокатки Vz має максимум при =30. Тобто, враховуючи, що при =30° розміри валків по всій своїй довжині пропорційно більші стосовно "зони" у відношенні 4:1 і мають великий діаметр на калібруючій ділянці, а також задовольняють умові відсутності скручування металу, тоді кут =30° схрещування найбільш оптимальний при побудові планетарної гвинтової кліті. При цих оптимальних параметрах гвинтової прокатки =30°, d r1 Р 40 45 ; 1 2 3 3 cos 2 габарити валків пропорційно більші, що необхідно для мінімального питомого їхнього зносу. 2 3 cos 2 tg і кутом валка =-. Це Відсутнє скручування металу за кутом зони tg 1 1 3 cos 2 важливо для планетарного виконання кліті, тому що підкат обертається з малою швидкістю, якщо не дотримується названа умова, незважаючи на те, що подвійний привод кліті автоматично настроюється на відсутність обертання розкату. Швидкість прокатки Vz='cddsin максимальна при зменшеному куті =30° через значне зменшення найкоротшої відстані d в області =40…60. І як наслідок, такий вибір параметрів d i зв'язує початкові кутові швидкості обертання центрального колеса і ротора в конкретну залежність від цих же параметрів Ц 35 1 3 cos 2 1 1 2 3сos 2 1 3 cos 2 2 3 cos 2 i . Таким чином, можна стверджувати, що процес планетарної cos 1 3 cos 2 гвинтової прокатки оптимізується за допомогою вищенаведених простих формул геометрії кліті і трьох її кінематичних критеріїв КВП1, КВП2, КВП3. Енергія, затрачувана на роботу деформації металу, визначається також із простих фізичних розумінь. Коли ротор кліті нерухомий, його привод не споживає енергію, метал при цьому cd cos . Центральне колесо кліті, відповідно до обертається з кутовою швидкістю M ' 1 cd кінематичної схеми (фіг. 3), обертається з кутовою швидкістю Ц=-МіМі2і1, а двигун центрального колеса здобуває швидкість ДВ,Ц=-ЦіЦ, де іЦ - передаточне число між центральним колесом і його двигуном. Якщо один валок сприймає момент навантаження від деформівного металу МН, тоді загальна потужність двигуна центрального колеса, необхідна для трьох валків кліті, Р=3МН'. У силу того, що споживана потужність не трансформується (тут ККД механізму приймаємо за одиницю), момент навантаження на цьому двигуні визначається з 7 UA 99867 C2 відомого 5 10 15 20 25 30 співвідношення MH,ДВ,Ц 3 МН ' ДВ,Ц 1 . iЦ і2 і1 При цьому метал обертається, передаючи своє аксіальне навантаження своїй нерухомій опорі, тобто - ротору. Як тільки, ротор відпускається в холостий спонтанний безперешкодний рух, процес прокатки зупиняється через те, що валки перестають обертатися щодо своїх осей, а обертаються разом з ротором тільки щодо осі прокатки. Тобто, поверхні валків уже не мають складової швидкості уздовж осі прокатки і метал не затягується у вогнище деформації. При цьому шестерні сателітів не мають відносного руху стосовно обертового центрального колеса, тобто холоста швидкість ротора стає рівною швидкості центрального колеса. А регульований привод центрального колеса при зникненні навантаження не йде в рознос через підтримку швидкості свого двигуна на заданому рівні. Це схоже на неможливість руху автомобіля, у приводі якого використовується диференціальний механізм, якщо на одному з коліс зникає навантаження. Щоб у процесі деформації металу зупинити його аксіальний рух, а метал мав можливість рухатися тільки уздовж осі прокатки, до ротора кліті необхідно прикласти активний момент, що компенсує аксіальне навантаження МН,М, прикладене до деформуючого металу. Швидкість обертання ротора повинна бути рівною зі зворотним знаком швидкості обертання металу при зупиненому роторі, але з умовою, що центральне колесо обертається з добавкою швидкості, рівної швидкості ротора, інакше центральне колесо буде перешкоджати руху ротора. Тобто, здається, що споживання енергії при планетарній гвинтовій прокатці більше, ніж при звичайній, тому що витрачається додаткова енергія в приводі центрального колеса, а також додаткова енергія в приводі ротора. Все це схоже на "парадокс споживання енергії", але цей парадокс необхідно згадати, тому що з подібними ефектами зустрічаються дослідники, що вивчають диференціальні механізми (Кудрявцев В.Н. Планетарные передачи. Издание второе, переработанное и дополненное, издательство "Машиностроение", Москва, 1966, Ленинград, 307 с, смотри 47-ю с.; Планетарные передачи. Справочник. Под ред. докторов технических наук В.Н. Кудрявцева и Ю.Н. Кирдяшева. Л., "Машиностроение", Ленингр. отд-ние, 1977, 536 с, смотри стр. 43…45). Тут відмічається, що в планетарних передачах зубчасті колеса крім корисної потужності, передають додаткову потужність, названу замкненою. Вона циркулює в механічному контурі також як і потужність у зачепленні, має розмірність потужності, але не є енергетичним поняттям. Для кліті із гіпоїдною передачею (фіг. 4), міркування ті ж, тільки центральне колесо обертається з "різницевою" швидкістю стосовно ротора. ' Отже, момент навантаження щодо осі z' на один робочий валок MH T SКОНТ fTP rCP . Момент навантаження щодо осі прокатки z, прикладений до деформованого металу від трьох валків, відповідно рівний MH,M 3 T SКОНТ fTP rCP cos . Потужність прокатки на трьох 35 валках швидкості входу заготовки в кліть V0='cddsin рівна V0 ' . Потужність, яку необхідно прикласти до приводу PПР 3 Т SКОНТ fTP rCP c d d sin ротора, РПР=3·МН·' щоб при зупинити Використовуючи обертання металу, PВР 3 T SКОНТ fTP rCP cos М . cd КВП2 М cos , критерій ' 1 c d другий cd cos . 1 c d колеса PВP 3 T SKOHT fTP rCP cos ' 40 центрального Сумарна потужність, прикладена і до ротора, c ' P PПР РВР 3 Т SKOHT fTP rCP '3 T SKOHT fTP rCP cos ' d cos 1 cd ' PПР rCP 1 c d . РВР rCP c d cos2 Кліть, що заявляється, гвинтова тривалкова планетарна консольна обтискна пояснюється кресленнями на фіг. 7, 8, 9, 10, 11, 12. На фіг. 7 показана схема планетарної гвинтової кліті з відомими параметрами =45, d=81.4 мм. Валки утворюють замкнений калібр, виконані максимальними, мають початковий і кінцевий радіуси нерозмірно великий і малий стосовно початку і кінцю "зони". Калібруюча їх ділянка має великий питомий знос інструмента. Кліть має властивість скручувати метал. розподіляється відповідно: 45 8 UA 99867 C2 5 10 15 20 25 30 На фіг. 8 показана пропонована кліть із оптимально вибраним кутом схрещування =30° і залежній від цього кута найкоротшою відстанню d=125 мм. Валки виконані із пропонованою умовою не скручування металу у зоні деформації, мають пропорційні розміри до цієї зони по всій своїй довжині у відношенні приблизно 4:1, близькі до максимальних пропорційних габаритів, що краще з погляду їх зносу. Кліть має максимальну швидкість прокатки, її ККД мало відрізняється від максимального у відповідності із оптимально вибраними характерними параметрами d і . Кліть складається із чотирьох складальних одиниць: механізм приводу кліті 1, механізм валків 2, корпус валків 3 і нерухомий корпус кліті 4. Механізм приводу кліті 1 має центральне колесо 5, зчленоване з механізмом валків 2, ротор 6 і ведучі шестерні 7, 8, що знаходяться у зачепленні із центральним колесом 5 і ротором 6. Механізм валків 2 із своїм корпусом валків 3 поміщені в ротор кліті 6. Ведучі шестерні 7, 8 з'єднані із двома двигунами, обороти яких вирівнюються за допомогою зовнішнього редуктора 9. На фіг. 9, 10 виконані 3-d моделі клітей з кутами =45° й =30°. Кліть із кутом =30° має правильні пропорції з погляду геометрії системи валки - метал. На фіг. 11 показана 3-d модель пропонованої кліті із зовнішнім редуктором, що мають конкретний коефіцієнт передачі, за допомогою якого вирівнюються обороти подвійного електропривода. На фіг. 12 показана технологічна схема застосування пропонованої кліті. Перевага даної кліті у великому ступені деформації за один прохід і можливості її стикування на вході з безперервним розливанням металу, а на виході - із клітями поздовжньої прокатки, де відбувається чистова обробка прокату. Кліть працює в такий спосіб. Ведуча шестірня 7 приводить в обертання центральне колесо 5, це колесо обертає механізм валків 2, валки обертаються навколо своїх осей. Ведуча шестірня 8 приводить в обертання ротор 6 навколо осі прокатки. При подачі заготовки в міжвалковий зазор валки затягують заготовку у зону деформації й обтискають її до заданого розміру без відносного скручування підкату і розкату. При цьому обертання заготовки компенсується обертанням ротора 6, швидкість якого знаходиться в визначеному початковому співвідношенні до швидкості центрального колеса 5. Розраховане початкове кінематичне співвідношення приводів планетарної кліті дозволяє автоматизованому подвійному електроприводу за допомогою датчика оборотів розкату забезпечити подальший рух деформованого металу тільки уздовж осі прокатки. Приклад конкретного виконання пропонованого обладнання розглянемо для умов роботи дротового стану 150 Макіївського металургійного заводу. З метою економії енергії можна сполучити з безперервним розливанням круглої заготовки 150 мм дві планетарні гвинтові кліті 2 35 2 150 50 із сумарною витяжкою 81 . Ці кліті заміняють обтискну і дві проміжні 50 16 .66 групи клітей поздовжньої прокатки, що полягають із 17=9+4+4 клітей згаданого стану 150, де 2 40 45 150 мм відбувається чорновий обтиск металу із загальною витяжкою 17 мм 78 . Далі в десятикліттьовому блоці із горизонтальних і вертикальних клітей, що чергуються, поздовжньої прокатки із сумарною витяжкою 8 одиниць розкат приймає кінцеві розміри дроту 6 мм. Отже, після безперервного розливання гаряча кругла заготовка 150 мм, проходячи через індукційний нагрів, де вирівнюється її температура, безупинно подається із середньою швидкістю 6 м 0,1 м в першу планетарну гвинтову кліть. Її кут схрещування і найкоротша хв с відстань між осями прокатки і валка відповідно рівні =30°, d125 мм. Як зрозуміло із представленої таблиці 1, поздовжня швидкість входу заготовки в кліть узгоджується із швидкістю розливання, якщо швидкість обертання валків V0 100 об . Метал деформується з витяжкою f' 0.319 2 c d d sin 2 3.14 0.79941 124 .63 0.5 с 2 2 r 75 0 9 r 25 1 при схрещеному куті зони деформації r r 75 25 rCP 0 1 50 мм , 2 2 як показує практика 0.79941)0.57735]=6.606°. Середній радіус зони деформації площа контакту металу і валка, 9 =arctg[(1-cd)tg]=arctg[(1 UA 99867 C2 2 rCP z 0 2 3.14 50 610 .6 15985 мм2 , границя текучості гарячого металу 6 2 62 Н Т 100 , сила прокатки F=TSKOHT=10015985=1598500H1600 kH, середній радіус валка мм2 SKOHT r' r' 100 264 ' rCP 1 0 182 мм 0,182 м , 2 2 M S 5 10 15 f r' коефіцієнт тертя fTP=0,3, момент прокатки 1600 0.3 0.182 87.36 кН м H T KOHT TP CP (навантаження) . Момент навантаження, прикладений до деформованого металу від трьох валків, Потужність MH,М 3 T SKOHT fTP rСР cos 3 1600 0.3 0.05 0.866 62.35 кН м . прокатки на трьох валках РПP=3·MH·' при швидкості входу заготовки в кліть V0='cddsin рівна V0 0,1 ' PПР 3 Т SKOHT f TP rCP 3 87,36 524,5 кВТ . Потужність, c d d sin 0,79941 0,125 0,5 прикладена до приводу ротора для зупинки обертання металу, cd 0.79941 PВР 3 Т SKOHT f TP rСР cos ' cos 62.35 2.007 0.866 431 .9 кВТ . 1 cd 1 0.79941 Частота обертання ротора і центрального колеса відповідно cd рад об Р ' cos 2.007 3.451 6.926 11 ; , 1 cd с с 1 сd рад 1 0.79941 об Ц Р 1 i1i 2 6.926 1 3 0.55 10.24 1.63 . c d cos 0.79941 0.866 с с Зовнішній редуктор з коефіцієнтом механічної передачі 1 сd 1 0.79941 іК 1 i 1 3 0.55 1.478 , з'єднаний із двигуном ротора, збільшує c d cos 0.79941 0.866 об з метою вирівнювання швидкості двох приводів. с кліті розкат діаметром 50 мм рухається із його обороти до 11 1 478 163 , , , На 20 виході з першої швидкістю м і входить у другу планетарну гвинтову кліть, яка повністю V1 V0 0,1 9 0,9 с геометрично подібна першій кліті в масштабі 1:3. Вихідні дані другої кліті зведено в таблицю 2. Зона деформації другої кліті має початковий і кінцевий радіуси r 0=25 мм, r1=8.33 мм. У другій кліті кут схрещування і найкоротша відстань між осями прокатки і валка відповідно рівні =30°, V0 900 об d42 мм. Частота обертання валків f ' . 8.63 2 c d d sin 2 3.14 0.79941 41.53 0.5 с 2 25 2 r 25 Метал деформується з витяжкою 0 9 при схрещеному куті зони r 8.33 1 деформації =arctg[(1-cd)tg]=arctg[(1-0.79941)0.57735]=6.606°. Середній радіус зони r0 r1 25 8.33 16 .7 мм , площа контакту металу і валка, як показує деформації rcp 2 2 2 rCP z 0 2 3.14 16.7 203 .5 практика SКОНТ 1780 мм2 , границю текучості гарячого 6 2 62 Н металу Т 100 , сила прокатки F=TSКОНТ=1001780=178000Н178 кН, середній радіус мм2 валка 30 r' r' 33.2 87.9 ' rCP 1 0 60.6 мм , 2 2 коефіцієнт тертя fTP=0,3, момент прокатки ' MH T SКОНТ fTP rCP 178 0.3 0.0606 3.24 кН м . (навантаження) Момент навантаження, прикладений до деформівного металу від трьох валків Потужність MH,М 3 T SКОНТ fTP rСР cos 3 178 0.3 0.01666 0.866 2.32 кН м . прокатки на трьох валках PПР=3·МН·' при швидкості входу заготовки в кліть V0='cddsin рівна 10 UA 99867 C2 V0 900 3 3.24 526 .87 кВТ . c d d sin 0.79941 41.54 0.5 Потужність, прикладена до приводу ротора для зупинки обертання металу cd 0.79941 PВР 3 Т SКОНТ f TP rСР cos ' cos 2.32 54.2 0.866 433 .97 кВТ . 1 cd 1 0.79941 Частота обертання ротора і центрального колеса відповідно cd рад об Р ' cos 54.19 3.451 187 29,76 ; 1 cd с с ' PПР 3 Т SКОНТ f TP rCP 5 1 сd рад 1 0.79941 об Ц Р 1 i1i 2 187 1 3 0.55 276 .48 44 . Зовнішній c d cos 0.79941 0.866 с с редуктор з коефіцієнтом механічної передачі 1 сd 1 0.79941 іК 1 i 1 3 0.55 1.478 , з'єднаний із двигуном ротора, вирівнює c d cos 0.79941 0.866 об . с У зв'язку з тим, що в другій кліті швидкості валків, ротора, центрального колеса в 27 разів більше, ніж в першій кліті, тоді внутрішня редукція приводу ротора і центрального колеса анулюється і виконується в співвідношенні 1:1. Отже, циліндричний нерухомий корпус другої кліті трансформується у форму куба, а електродвигуни, один з них із пропонованим редуктором, установлюються по різні сторони кліті. Усе це не змінює суть пропонованого винаходу, тому на технологічній схемі фіг. 12 зазначена корекція другої кліті конкретно не показана. Другу кліть просто виконано в масштабі 1:3 стосовно першої. Кінематика і динаміка гвинтової прокатки у великій і малій клітях протилежні один одному. його обороти із двигуном центрального колеса 29,79 1478 44 , 10 15 3 M1 r0 2 обернено пропорціональне r M2 1 1 відношенню кутових швидкостей валків і рівне в кубі коефіцієнта геометричної подоби деформуючого металу в цих клітях. Тобто, у споживанні енергії дві кліті повністю ідентичні за умови рівності витяжок. Якщо мати справу з енергією такого складного об'єкта, значно полегшуються будь-які розрахунки розглянутої технології. А якщо керувати енергією або потужностями активних елементів кліті або електроприводами, а їх чотири у двох клітях, тоді узгодження загальної їхньої роботи більш оптимально здійснюється регуляторами потужностей усіх зв'язаних приводів. Тому указана керована робота двох гвинтових агрегатів буде узгоджена з наступними елементами прокатного стану і попереднім тягнучим пристроєм безперервного розливання. Здавалося б, таке технологічно необхідне велике геометричне співвідношення двох клітей за збереженням споживаних потужностей (однакові витяжки), нелінійним чином вплине на розміри електродвигунів, у яких потужності повинні бути однаковими. Однак відомо, що в асинхронних двигунах з однаковими потужностями з ростом номінального моменту і з паралельним зменшенням швидкості, їх діаметр також росте пропорційно числу пар полюсів. На стані 150 чорнова обробка металу в 17 - і клітях проводиться встановленою потужністю електроприводів на один рівчак близько 10 Мвт, що в п'ять раз більше пропонованої технології обтиску металу на двох гвинтових клітях. Відомо, що останнім часом обтискна група горизонтальних клітей поздовжньої прокатки комплектується вертикальними клітями, які чергуються, що дозволило ліквідувати операцію кантування металу. Але кількість клітей можливо значно зменшити, застосовуючи тільки технологію гвинтової прокатки в планетарному виконанні. Тому й ця модернізована технологія поздовжньої прокатки уступає пропонованій технології, де обтиск металу з великою витяжкою здійснюється з мінімальним його розширенням, за рахунок чого і заощаджується споживана енергія. Кліть гвинтова тривалкова планетарна консольна обтискна, що заявляється, забезпечує оптимальну технологію прокатки за рахунок вибору оптимального кута схрещування між осями прокатки і валка, що видно з наведених таблиць, кінематичних співвідношень механізму подвійного приводу кліті і профілювання валків і зони деформації. Прокатка в кліті, що заявляється, де радіуси валків пропорційно більше радіусів зони деформації у співвідношенні 4:1 забезпечує мінімальний знос валків, дозволяє вести процес деформації без обертання і Відношення моментів прокатки у двох клітях 20 25 30 35 40 45 11 UA 99867 C2 скручування металу при великій витяжці і малих енерговитратах з максимальною швидкістю прокатки завдяки оптимальному співвідношенню характерних геометричних параметрів гвинтової прокатки d і . Таблиця 1 r0=75 мм, r1=25 мм, '=2.007 рад/с 1 2 3 , град сd d, мм 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 0,85076 0,84858 0,84625 0,84376 0,8411 0,83826 0,83526 0,83207 0,8287 0,82513 0,82137 0,81741 0,81324 0,80886 0,80425 0,79941 0,79433 0,78901 0,78343 0,77758 0,77146 0,76506 0,75837 0,75137 0,74405 0,7364 0,72842 0,72008 0,71138 0,70229 0,69282 0,68294 0,67264 0,66191 0,65074 0,6391 0,62699 0,61439 0,6013 0,58769 0,57356 0,55891 0,54371 0,52798 0,5117 0,49487 167,51 165,106 162,602 160,006 157,327 154,572 151,751 148,871 145,94 142,967 139,958 136,921 133,864 130,792 127,712 124,631 121,554 118,487 115,434 112,401 109,392 106,412 103,463 100,549 97,6746 94,8415 92,0528 89,3108 86,6176 83,9753 81,3856 78,8499 76,3696 73,9457 71,5794 69,2714 67,0223 64,8328 62,7033 60,6341 58,6255 56,6775 54,7902 52,9636 51,1977 49,4924 4 ' r1 , мм 142,51 140,106 137,602 135,006 132,327 129,572 126,751 123,871 120,94 117,967 114,958 111,921 108,864 105,792 102,712 99,6311 96,5542 93,4869 90,4344 87,4014 84,3924 81,4115 78,4627 75,5493 72,6746 69,8415 67,0528 64,3108 61,6176 58,9753 56,3856 53,8499 51,3696 48,9457 46,5794 44,2714 42,0223 39,8328 37,7033 35,6341 33,6255 31,6775 29,7902 27,9636 26,1977 24,4924 5 , град 2,29 2,4861 2,6913 2,9062 3,1318 3,369 3,6185 3,8815 4,1589 4,4518 4,7614 5,089 5,4358 5,8032 6,1928 6,6061 7,0448 7,5108 8,0058 8,532 9,0915 9,6866 10,32 10,993 11,71 12,472 13,283 14,146 15,064 16,04 17,076 18,176 19,343 20,58 21,889 23,273 24,732 26,269 27,883 29,575 31,342 33,183 35,093 37,067 39,1 41,183 5 12 6 7 8 min, град , град max, град 2,047 2,19 2,333 2,478 2,623 2,771 2,919 3,07 3,222 3,375 3,531 3,689 3,848 4,01 4,174 4,341 4,51 4,682 4,857 5,035 5,216 5,4 5,588 5,78 5,975 6,174 6,378 6,586 6,798 7,016 7,239 7,467 7,701 7,941 8,187 8,439 8,699 8,966 9,24 9,522 9,813 10,11 10,42 10,74 11,07 11,41 12,71 13,514 14,309 15,094 15,868 16,631 17,381 18,119 18,841 19,548 20,239 20,911 21,564 22,197 22,807 23,394 23,955 24,489 24,994 25,468 25,908 26,313 26,68 27,007 27,29 27,528 27,717 27,854 27,936 27,96 27,924 27,824 27,657 27,42 27,111 26,727 26,268 25,731 25,117 24,425 23,658 22,817 21,907 20,933 19,9 18,817 12,953 13,81 14,667 15,522 16,377 17,229 18,081 18,93 19,778 20,625 21,469 22,311 23,152 23,99 24,826 25,659 26,49 27,318 28,143 28,965 29,784 30,6 31,412 32,22 33,025 33,826 34,622 35,414 36,202 36,984 37,761 38,533 39,299 40,059 40,813 41,561 42,301 43,034 43,76 44,478 45,187 45,887 46,578 47,259 47,93 48,59 9 z0, мм (при min) 1977,9131 1849,3634 1735,6358 1634,2596 1543,2842 1461,1492 1386,5914 1318,5773 1256,253 1198,907 1145,9417 1096,8514 1051,2052 1008,6341 968,81961 931,48599 896,39301 863,33048 832,11372 802,57982 774,58449 747,99951 722,71058 698,61544 675,62237 653,64887 632,62053 612,47009 593,13659 574,56468 556,70399 539,50862 522,93662 506,94965 491,51255 476,5931 462,16168 448,19106 434,65617 421,53393 408,80304 396,44388 384,4383 372,76959 361,42231 350,38219 UA 99867 C2 Продовження табл. 1 1 10 , град z0, мм (при ) 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 1768,206 1628,589 1504,291 1392,854 1292,337 1201,187 1118,147 1042,186 972,4517 908,2319 848,9262 794,0245 743,0901 695,7465 651,6668 610,5654 572,1913 536,3226 502,7624 471,3345 441,881 414,2597 388,3419 364,0106 341,1593 319,6907 299,5152 280,5507 262,7214 245,9573 230,1932 215,369 201,4286 188,3196 175,9933 164,404 153,509 143,2682 133,6442 124,6015 116,1069 108,1292 100,6387 93,60781 87,01009 80,82071 11 z '0 , мм (при max, min) 1928,8187 1797,2127 1680,4706 1576,124 1482,225 1397,2156 1319,8351 1249,0523 1184,0158 1124,0167 1068,4595 1016,841 968,7327 923,76768 881,62994 842,04587 804,77747 769,61672 736,38108 704,90973 675,06044 646,70701 619,73708 594,05032 569,55687 546,17603 523,83515 502,46866 482,0172 462,427 443,64917 425,63918 408,35643 391,7638 375,82727 360,51566 345,80028 331,65474 318,05467 304,97757 292,40259 280,31041 268,68307 257,50384 246,75713 236,42834 12 z '0 , мм (при , ) 1726,2572 1584,991 1459,2347 1346,5336 1244,9495 1152,9309 1069,2204 992,78664 922,77541 858,47178 799,27204 744,66197 694,20007 647,50432 604,24181 564,12045 526,88234 492,29835 460,1638 430,29488 402,5257 376,70584 352,69836 330,37811 309,63028 290,3492 272,43736 255,80449 240,36686 226,0466 212,77118 200,4729 189,08848 178,55868 168,828 159,84435 151,55884 143,92551 136,90113 130,44505 124,51898 119,08686 114,11475 109,57064 105,42439 101,6476 13 13 ' r0 , мм (при max, min) 465,9485 463,4665 460,852 458,1093 455,2422 452,2549 1 449,1514 445,9356 442,6111 439,1818 435,6512 432,0227 428,2997 424,4854 420,5828 416,5948 412,5244 408,3741 404,1467 399,8445 395,4701 391,0258 386,5138 381,9364 377,2958 372,5942 367,8336 363,0162 358,144 353,2194 348,2443 343,221 338,1517 333,0387 327,8843 322,6909 317,4609 312,1971 306,9019 301,5781 296,2285 290,8561 285,464 280,0552 274,6331 269,201 14 ' r0 , мм (при , ) 414,606 405,877 396,813 387,448 377,816 367,953 357,891 347,664 337,305 326,845 316,315 305,745 295,162 284,593 274,064 263,599 253,22 242,949 232,804 222,804 212,965 203,302 193,829 184,558 175,5 166,665 158,061 149,695 141,574 133,701 126,082 118,719 111,615 104,77 98,1854 91,8608 85,7951 79,9868 74,4338 69,1333 64,082 59,2764 54,7123 50,3851 46,2901 42,422 UA 99867 C2 Продовження табл. 1 1 , град 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 15 Zoтн, z0=600 3,58188 3,63403 3,68999 3,74986 3,81372 3,88168 3,95385 4,03034 4,11127 4,19678 4,287 4,38208 4,48218 4,58745 4,69806 4,81421 4,93607 5,06385 5,19776 5,33801 5,48484 5,63849 5,79919 5,96722 6,14285 6,32634 6,518 6,71811 6,92699 7,14495 7,37231 7,6094 7,85653 8,11406 8,3823 8,66159 8,95224 9,25457 9,56887 9,89542 10,2345 10,5862 10,9509 11,3285 11,7193 12,1231 16 KВПср 0,2380406 0,2506284 0,2626419 0,2740641 0,2848806 0,2950806 0,304656 0,3136015 0,3219149 0,3295965 0,3366492 0,3430783 0,3488915 0,3540982 0,3587101 0,3627401 0,3662032 0,3691152 0,3714934 0,373356 0,374722 0,3756113 0,3760441 0,3760414 0,3756241 0,3748136 0,3736315 0,3720994 0,3702387 0,368071 0,3656176 0,3628996 0,3599381 0,3567538 0,3533671 0,3497984 0,3460674 0,3421938 0,3381971 0,3340963 0,3299103 0,3256578 0,3213571 0,3170266 0,3126843 0,3083483 14 17 Vz, мм/с 74,04164 77,52288 80,75978 83,74729, 86,48174 88,96077 91,18326 93,1493 94,86013 96,31805 97,52638 98,48933 99,212 99,70021 99,96049 100 99,82641 99,44786 98,87289 98,11036 97,1694 96,05934 94,78966 93,36995 91,80983 90,11894 88,3069 86,38325 84,35743 82,23879 80,0365 77,75956 75,41681 73,01686 70,56813 68,07879 65,55679 63,00984 60,44541 57,8707 55,29268 52,71807 50,15331 47,60463 45,07798 42,57909 UA 99867 C2 Таблиця 2 r0=25 мм, r1=8,333 мм, '=54,2001 рад/с 1 2 3 , град сd d, мм 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 0,85076 0,84858 0,84625 0,84376 0,8411 0,83826 0,83526 0,83207 0,8287 0,82513 0,82137 0,81741 0,81324 0,80886 0,80425 0,79941 0,79433 0,78901 0,78343 0,77758 0,77146 0,76506 0,75837 0,75137 0,74405 0,7364 0,72842 0,72008 0,71138 0,70229 0,69282 0,68294 0,67264 0,66191 0,65074 0,6391 0,62699 0,61439 0,6013 0,58769 0,57356 0,55891 0,54371 0,52798 0,5117 0,49487 55,8364 55,0351 54,2005 53,3352 52,442 51,5239 50,5834 49,6234 48,6465 47,6554 46,6525 45,6402 44,621 43,5971 42,5706 41,5435 40,5179 39,4955 38,478 37,467 36,464 35,4704 34,4874 33,5163 32,5581 31,6137 30,6841 29,7701 28,8724 27,9917 27,1284 26,2832 25,4564 24,6485 23,8597 23,0904 22,3407 21,6109 20,901 20,2113 19,5417 18,8924 18,2633 17,6545 17,0658 16,4974 4 ' r1 , мм 47,5031 46,7018 45,8672 45,0019 44,1087 43,1906 42,2501 41,2901 40,3132 39,3221 38,3192 37,3069 36,2877 35,2638 34,2373 33,2102 32,1846 31,1622 30,1447 29,1337 28,1307 27,1371 26,1541 25,183 24,2248 23,2804 22,3508 21,4368 20,5391 19,6584 18,7951 17,9499 17,1231 16,3152 15,5264 14,7571 14,0074 13,2776 12,5677 11,878 11,2084 10,5591 9,93002 9,32118 8,73255 8,16409 5 , град 2,29 2,486 2,691 2,906 3,132 3,369 3,619 3,881 4,159 4,452 4,761 5,089 5,436 5,803 6,193 6,606 7,045 7,511 8,006 8,532 9,092 9,687 10,32 10,99 11,71 12,47 13,28 14,15 15,06 16,04 17,08 18,18 19,34 20,58 21,89 23,27 24,73 26,27 27,88 29,57 31,34 33,18 35,09 37,07 39,1 41,18 15 6 7 8 min, град , град max, град 2,047 2,19 2,333 2,478 2,623 2,771 2,919 3,07 3,222 3,375 3,531 3,689 3,848 4,01 4,174 4,341 4,51 4,682 4,857 5,035 5,216 5,4 5,588 5,78 5,975 6,174 6,378 6,586 6,798 7,016 7,239 7,467 7,701 7,941 8,187 8,439 8,699 8,966 9,24 9,522 9,813 10,11 10,42 10,74 11,07 11,41 12,71 13,514 14,309 15,094 15,868 16,631 17,381 18,119 18,841 19,548 20,239 20,911 21,564 22,197 22,807 23,394 23,955 24,489 24,994 25,468 25,908 26,313 26,68 27,007 27,29 27,528 27,717 27,854 27,936 27,96 27,924 27,824 27,657 27,42 27,111 26,727 26,268 25,731 25,117 24,425 23,658 22,817 21,907 20,933 19,9 18,817 12,953 13,81 14,667 15,522 16,377 17,229 18,081 18,93 19,778 20,625 21,469 22,311 23,152 23,99 24,826 25,659 26,49 27,318 28,143 28,965 29,784 30,6 31,412 32,22 33,025 33,826 34,622 35,414 36,202 36,984 37,761 38,533 39,299 40,059 40,813 41,561 42,301 43,034 43,76 44,478 45,187 45,887 46,578 47,259 47,93 48,59 9 z0, мм (при min) 659,30471 616,45479 578,54556 544,75347 514,42833 487,04999 462,19738 439,52598 418,7512 399,63586 381,98075 365,6173 350,40192 336,21153 322,94003 310,49549 298,79782 287,77697 277,37138 267,52674 258,19496 249,3333 240,90365 232,87193 225,20757 217,88307 210,87362 204,1568 197,71229 191,52165 185,56809 179,8363 174,31229 168,9833 163,8376 158,86445 154,05397 149,39709 144,88546 140,51138 136,26775 132,14802 128,14616 124,25659 120,47416 116,79412 UA 99867 C2 Продовження табл. 2 1 10 , град z0, мм (при ) 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 589,4023 542,8634 501,4307 464,2849 430,7791 400,3958 372,7158 347,3955 324,1507 302,7441 282,9755 264,6749 247,6968 231,9156 217,2224 203,5219 190,7305 178,7743 167,5875 157,1116 147,2937 138,0866 129,4474 121,3369 113,7198 106,5636 99,83844 93,51695 87,57386 81,98579 76,73111 71,78971 67,14289 62,77323 58,66445 54,80135 51,16968 47,7561 44,54808 41,53385 38,70232 36,04307 33,54626 31,20262 29,00338 26,94025 11 12 z '0 13 ' r0 , мм , мм z '0 , мм (при , ) (при max, min) (при max, min) 642,93987 575,41934 155,3162 599,07121 528,3306 154,4888 560,15714 486,41181 153,6174 525,37494 448,84475 152,7031 494,07526 414,98337 151,7474 465,73878 384,3105 150,7517 439,94524 356,40696 149,7172 416,35096 330,92904 148,6452 394,67214 307,59196 147,5371 374,67241 286,1574 146,394 356,15334 266,42415 145,2171 338,94717 248,22078 144,0076 322,91106 231,40014 142,7666 307,92271 215,83488 141,4952 293,87679 201,41404 140,1943 280,6821 188,04024 138,865 268,25929 175,62753 137,5082 256,53903 164,09953 136,1247 245,46048 153,38801 134,7156 234,97003 143,4317 133,2815 225,02026 134,1753 131,8234 215,56911 125,56867 130,342 206,57913 117,56618 128,838 198,01687 110,12609 127,3122 189,85238 103,21014 125,7653 182,05877 96,783115 124,1981 174,61181 90,812498 122,6112 167,48964 85,268206 121,0054 160,67248 80,122327 119,3814 154,14241 75,348906 117,7398 147,88313 70,923764 116,0815 141,8798 66,824334 114,407 136,11888 63,029524 112,7173 130,588 59,51959 111,0129 125,27582 56,276027 109,2948 120,17195 53,281477 107,5637 115,26682 50,519639 105,8204 110,55164 47,975193 104,0657 106,01828 45,633734 102,3007 101,65924 43,481706 100,5261 97,467579 41,506347 98,74288 93,43685 39,695641 96,95208 89,561068 38,038268 95,1547 85,834658 36,523564 93,35177 82,252418 35,14148 91,5444 78,809485 33,882549 89,73372 16 14 ' r0 , мм (при , ) 138,202 135,292 132,271 129,149 125,939 122,651 119,297 115,888 112,435 108,948 105,438 101,915 98,3872 94,8643 91,3547 87,8664 84,4068 80,9829 77,6013 74,2679 70,9882 67,7673 64,6096 61,5194 58,5001 55,5551 52,687 49,8984 47,1912 44,567 42,0273 39,573 37,2049 34,9233 32,7285 30,6202 28,5983 26,6623 24,8112 23,0444 21,3607 19,7588 18,2374 16,795 15,43 14,1407 UA 99867 C2 Продовження табл. 2 1 , град 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 15 Zoтн, z0=200 3,581893 3,634042 3,690006 3,749871 3,813735 3,881696 3,953864 4,030354 4,111289 4,196798 4,28702 4,3821 4,482194 4,587463 4,69808 4,814226 4,936089 5,063871 5,197779 5,338034 5,484864 5,638509 5,799217 5,967248 6,142873 6,326369 6,518026 6,718142 6,927023 7,144982 7,372342 7,609426 7,856566 8,114092 8,382334 8,661622 8,952276 9,254605 9,568907 9,895456 10,2345 10,58626 10,95091 11,32857 11,71931 12,12313 16 KВПср 0,2380404 0,2506282 0,2626417 0,2740638 0,2848803 0,2950803 0,3046556 0,3136011 0,3219145 0,329596 0,3366487 0,3430778 0,3488909 0,3540976 0,3587094 0,3627395 0,3662025 0,3691145 0,3714926 0,3733552 0,3747212 0,3756105 0,3760433 0,3760405 0,3756232 0,3748127 0,3736307 0,3720985 0,3702378 0,3680701 0,3656166 0,3628987 0,3599372 0,3567529 0,3533662 0,3497974 0,3460664 0,3421929 0,3381961 0,3340954 0,3299094 0,3256568 0,3213562 0,3170257 0,3126834 0,3083474 17 Vz, мм/с 666,3747 697,706 726,838 753,7256 778,3357 800,6469 820,6493 838,3437 853,7411 866,8625 877,7374 886,404 892,908 897,3018 899,6444 900 898,4377 895,0307 889,856 882,9932 874,5246 864,5341 853,107 840,3295 826,2884 811,0705 794,7621 777,4492 759,2169 740,1491 720,3285 699,8361 678,7513 657,1518 635,1132 612,7091 590,0111 567,0886 544,0087 520,8363 497,6341 474,4626 451,3798 428,4417 405,7019 383,2118 ФОРМУЛА ВИНАХОДУ 5 Кліть гвинтова тривалкова планетарна консольна обтискна, що містить розміщений у нерухомому корпусі механізм приводу кліті з центральним колесом і ротором, механізм валків зі своїм корпусом, поміщений у ротор кліті та зчленований з центральним колесом, при цьому осі робочих валків схрещуються з віссю прокатки під кутом і зміщені перпендикулярно осі 17 UA 99867 C2 прокатки на найкоротшу відстань d довжину z'0 z0 2 2 r0 r1 z0 tg r1 , а самі валки мають радіус r' z' c2d2 z'2 tg2 , d 1 cd cos 2 і відповідну їм зону деформації з радіусом r z r1 z2tg2 , довжиною cos , обмежені кутом валка sin MAX 3 sin 2 і відповідно кутом зони деформації MIN MAX , яка відрізняється тим, що механізм валків установлений так, що кут 5 схрещування осей валків і прокатки становить 30 , кут зони деформації arctg 1 c d tg30 , відповідно кут валка 30 arctg 1 c d tg30 , при цьому центральне колесо кліті встановлено з можливістю обертання відносно ротора з початковою кутовою швидкістю Ц Р 1 і ім , а до приводу ротора або центрального колеса, відповідно при парній або непарній кількості ступенів передач валкового механізму, з'єднаний зовнішній редуктор з коефіцієнтом механічної передачі 10 1 cd iK 1 c cos i d ( 1) n , де r0 , r1 - радіуси підкату і розкату; cd 2 3 cos2 1 3 cos2 ; z' - вісь валка, координати точок якої відлічуються від найкоротшої відстані d ; z - вісь прокатки, координати точок якої відлічуються від найкоротшої відстані d ; 15 i 1n i1 i2 ...in - сумарний коефіцієнт передачі валкового механізму, n - кількість ступенів передач цього механізму; iM 1 cd ' - коефіцієнт передачі обертання валка ' і металу M ; M c d cos Ц - кутова швидкість обертання центрального колеса; P 20 - кутова швидкість обертання ротора, рівна зі зворотним знаком кутовій швидкості обертання металу P M при нерухомому роторі кліті; ' V0 - початкова кутова швидкість валка при заданій швидкості V0 входу заготовки в d c d sin кліть. 18 UA 99867 C2 19 UA 99867 C2 20 UA 99867 C2 21 UA 99867 C2 22 UA 99867 C2 23 UA 99867 C2 24 UA 99867 C2 25 UA 99867 C2 26 UA 99867 C2 27 UA 99867 C2 28
ДивитисяДодаткова інформація
Назва патенту англійськоюThree-roll screw planetary cantilevered breakdown stand
Автори англійськоюLytvynov Viktor Ivanovych, Zhukova Natalia Viktorivna, Lytvynova Taisia Serafimivna
Назва патенту російськоюКлеть винтовая трехвалковая планетарная консольная обжимная
Автори російськоюЛитвинов Виктор Иванович, Жукова Наталья Викторовна, Литвинова Таисия Серафимовна
МПК / Мітки
МПК: B21B 13/12, B21B 13/20, B21B 19/00
Мітки: консольна, обтискна, планетарна, тривалкова, гвинтова, кліть
Код посилання
<a href="https://ua.patents.su/31-99867-klit-gvintova-trivalkova-planetarna-konsolna-obtiskna.html" target="_blank" rel="follow" title="База патентів України">Кліть гвинтова тривалкова планетарна консольна обтискна</a>
Попередній патент: Стіновий захист верхівки нагрівальної стінки між двома отворами пічних камер коксової батареї
Наступний патент: Фармацевтична композиція у формі мазі
Випадковий патент: Спосіб гідродинамічної штамповки та пристрій для його здійснення