Суматор у парафазному коді

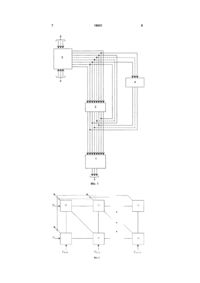
Суматор у парафазному коді, який містить блок регістра результату, блок матриці корекції переносу, блок матриці додавання і блок комута 3 18621 4 тього блоку, включеного послідовно з першими Матриця 2 корекції переносу являє собою двома, що значно зменьшує швидкодію. прямокутну матрицю елементів И 11 (Фіг. 2). Задачею корисної моделі є удосконалення суМатриця 2 корекції переносу містить тільки ті матора шляхом видалення шифратора і блоку елементи, що відповідають (N-1-1)-им позиціям контролю та вдосконалення регістру результату, кодового слова результату (де 1 - номера позицій блоку комутації та матриці додавання. цього слова, що залежать від переносу з молодЦе дозволяє забезпечити підвищення достовішого розряду ( 0 1 N ). Якщо прийнятий алфарності зберігання та обробки інофрмації та скоровіт, у якому кодові слова, що відповідають будьчення ступеней у ланцюгу обробки інформації. яким, двом сусіднім (в алфавіті) цифрам, відрізняПоставлена задача вирішується тим, що в суються один від одного тільки однією позицією (по маторі у парафазному коді, який містить блок регірівнях напруг у ній), то матриця має мінімальні стру результату, блок матриці корекції переносу, розміри (2хр), кожен вхід матриці 2 корекції переблок матриці додавання і блок комутації, причому носу з’єднані тільки з однією координатною шиною входи блоку матриці додавання з’єднані з вхідниїї. Якщо прийнятий алфавіт, у якому розходження ми шинами першого і другого операндів суматора, між кодовими словами, що відповідають сусіднім а перша група виходів блоку матриці додавання цифрам максимальні, то матриця корекції переноз’єднана з вхідними шинами суми блоку регістру су має також максимальні розміри (3хр), кожен результату, згідно з винаходом, в нього друга грувхід першої групи входів матриці корекції переносу па через блок матриці корекції переносу і третя з’єднаний з відповідними j-ми ( 1 j M ) координагрупа через блок комутації з’єднані з блоком регістними шинами кожен вхід другої групи - з однією тру результату. шиною. Виходи елементів И матриці корекції пеВидалення шифратору та блоку контролю та реносу, що відповідають однаковим позиціям ковдосконалення регістру результату, блоку комутадового слова результату, з’єднані вхідними діагоції та матриці додавання вигідно відрізняє запрональними шинами з відповідними виходами понований суматор від прототипу, оскільки виклюматриці 2 корекції переносу. чає виникнення помилкових комбінації при обробці Матриця 3 додавання являє собою матрицю інформації та її зберіганні. В результаті зменьшубагатовходових елементів И. Кількість входів кожється кількість ступеней у ланцюгу обробки інорного елемента И дорівнює 2М . Входи елементів И мації, і як наслідок, підвищюється достовірність з’єднані з визначеними шинами кодів операндів тривалого зберігання та обробки інформації. відповідно до обраного алфавіту. Шини кодів опеНа фіг.1 зображена блок-схема суматора у парандів з’єднані з входами матриці додавання. Корафазному коді. На фіг.2 - блок схема матриці жен елемент И має по два гальванічне незалежкорекції переносу. На фіг.3 - блок схема матриці них виходи. Перші, виходи елементів, що додавання. На фіг.4 - схеми формування значень відповідають однаковим переносам у наступний напівсуми в і-му розряді. розряд, з’єднані шинами з першою групою виходів Суматор містить регістр результату - 1, матриматриці додавання. Другі виходи, що відповідають цю корекції переносу - 2, матрицю додавання - 3 й однаковим результатам додавання в даному розблок комутації - 4. ряді, з’єднані шинами з другою групою виходів Входи матриці додавання з’єднані з вхідними матриці 3 додавання. шинами першого 5 і другого 6 операндів суматора. Блок 4 комутації представляє, собою групу з Перша група виходів матриці 3 з’єднані з вхідними ЧИ елементів, де 0 L M , у залежності від обшинами суми регістра результату. Друга група раного алфавіту. Входи блоку комутації, що відповиходів матриці 3 додавання з’єднана з першою відають кожної незалежної від переносу і повтогрупою входів матриці 2 корекції переносу, ті з рюваної позиції в кодових словах (представлених виходів, яким відповідають незалежні від переносу у коді, протилежному коду 1 з 2 по рівнях напруг) неповторювані позиції в кодових словах усіх можусіх можливих результатів, з’єднані з входами того ливих результатів, з’єднані безпосередньо з відсамого ЧИ елемента. Виходи ЧИ елементів є виповідними входами другої групи входів регістра ходами блоку. Існує залежність між числом ЧИ результату, інші виходи другої групи виходів мателементів блоку 4 комутації і числом елементів И риці додавання, яким відповідають незалежні від 11 блоку 2. Якщо блок 2 містить мінімальне число переносу повторювані позиції в кодових словах елементів И 11(2хр),то Число елементів блоку 4 усіх можливих результатів, з’єднані з входами комутації максимально L=М. Якщо блок 2 містить блоку комутації 4. Виходи матриці корекції переномаксимальне число елементів И (3хр), те L=0, тобсу з’єднані з однією групою входів регістра 1 рето необхідність у блоці 4 комутації відпадає. зультату. Виходи блоку комутації 4 з’єднані з відОперанди в коді „1 з 2” поступають з пам’яті на повідними входами другої групи входів регістра входи матриці додавання 3. Якщо поступають результату. Виходи регістру результату 7 з’єднані правильні кодові слова операндів, спрацьовує шиною з пам’яттю, куди зберігається остаточний один з елементів И матриці 3 та з його виходів результат додавання. сигнал, що відповідає результату операції постуСуматор працює в такий спосіб. пає на один з входів блоку корекції переносу 2 та Регістр 1 результату являє собою групу з N на один з входів блоку комутації 4. С одного з витригерів, одиничні входи яких утворять першу груходів блоку переносу 2 сигнал, що відповідає „0” пу входів, а нульові - другу групу входів регістра 1. або „1”, поступає в вихідну шину, якщо розглянуОдиничні виходи тригерів утворять групу виходів тий суматор є частиною багаторозрядного прирегістра 1, а нульові виходи приєднані до блоку строю. З виходу блоку комутації сигнали протилеконтролю. 5 18621 6 жні (по рівням напруг) результату операції в коді „1 наступною, більш старшою виглядає наступним з 2”, поступають на нульові входи тригерів регістру чином. 1, попередньо встановлених в одиничний стан. На виходах регістру 1 результату створюється кодове 1i 1 Z i,01Z i 1,01Z i 2,01Z i 3,01 1i 4 Z i,01Z i 1,01Z і 2,01 слово, яке відповідає результату операції в коді „1 Z i 3,10 Z i,01Z i 1,01Z i 2,10 Z i,01Z i 1,10 ( Z i,10 Z i 1,10 ). з 2”. Поява помилкових кодових слів операндів з меньшою, чим потрібно, кількістю „одиниць” призПовна множина категорій помилок, що можливодить до відсутності сигналів на всіх виходах ві в і-му розряді при представленні інформації паелементів матриці 3. Поява помилкових кодових рафазним кодом: слів операндів з більшою, чим потрібно, кількістю - перша - ai1 ai0 - не представлено ні одну „одиниць” призводить до появи на виходах елемецифру; нтів И матриці 3 одразу декількох сигналів, які по- друга - ai1 ai0 - представлено дві цифри тім шифруються в коді, оберненому (по рівням напруг) коду „1 з 2”, блоком комутації 4 як резульодночасно; тат декількох правильних операцій, які з’явилися - третя - представлена тільки одна цифра, але одночасно. Внаслідок цього на виходах блоку копомилково. мутації 4 з’являється кодове слово з більшою, чим Виявлення помилок перших двох категорій запотрібно, кількістю „одиниць”. Сигнали, які відповібезпечується з методичною імовірністю Рml=1, а дають „одиницям” цього кодового слова поступатретьої з імовірністю Рml=0. Отже вірогідність Dl ють на нульові входи відповідних тригерів (попецифрової інформації, повністю визначається іморедньо встановлених в одиничний стан) регістру 1. вірністю R3, утворення помилки третьої категорії: На виходах регістру 1 результату створюється Dl=1-R3. кодове слово з меньшою, чим потрібно кількістю Утворення помилок третьої R3 категорії мож„одиниць”. Як вже раніше говорилося, таке кодове ливо при спільному прояві помилок перших двох слово не може бути дешифроване як вірне і, таким tk категорій у перебігу часу t a * tk , де чином помилка не отримує подальшого розповсюрозв’язна здатність автоматичного контролю за дження. часом; 0