Спосіб перевірки вірогідності вимірювання параметрів руху космічного апарата

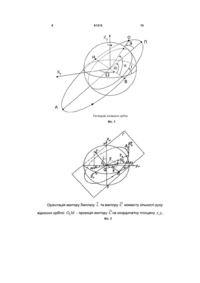
Спосіб перевірки вірогідності вимірювання параметрів руху космічного апарата, який полягає в тому, що в обчислювальній машині бортового комплексу керування дані з апаратури супутникової навігації ( xi, y, z, Vxi , Vyi , Vzi ) (координати та Корисна модель належить до галузі навігаційного забезпечення керування космічними апаратами, зокрема, до підсистем навігаційного забезпечення космічних апаратів (КА) та може бути використана в навігаційних системах вітчизняних космічних апаратів, що працюють в умовах однопунктної технології, для роботи бортових комплексів керування КА та їх навігаційної апаратури[1]. Відомі способи перевірки вірогідності параметрів руху КА проводять лише відбраковування аномальних вимірювань, отриманих з апаратури автономної супутникової навігації. Також в навігаційному приймачі різноманітними методами здійснюється згладжування та виділення навігаційних даних[2]. Недоліком відомих способів, обраних як прототип, є те, що на даний час на космічний апарат в космічному просторі діють ряд збурень, які вносять до характеристик прийнятих сигналів значні помилки, які неможливо розпізнати та відкинути, використовуючи стандартизоване програмне та математичне забезпечення, що призводить до значного погіршення точності визначення параметрів руху КА. Поряд з тим критичні збурення в штучних навігаційних полях іноземних держав викликані природними чи штучними причинами унеможливлюють якісне виконання координатних процедур керування. У основу корисної моделі покладено завдання створити спосіб перевірки вірогідності вимірювання параметрів руху КА, який шляхом прийняття рішень про достовірність даних, отриманих з апаратури супутникової навігації, дав можливість за безпечити незалежність від штучних навігаційних полів при виконанні координатних процедур керування, високу точність та достовірність визначення параметрів руху КА, нечутливих до малих відхилень та великих збурень, викликаних випадковими та цілеспрямованими завадами. Для рішення поставленого завдання у способі перевірки вірогідності вимірювання параметрів руху КА, який полягає в тому, що в обчислювальній машині бортового комплексу керування дані з апаратури супутникової навігації ( xi, y, z, Vx i , Vy i , Vzi ) (координати та швидкості) пе та швидкостей космічного апарата (КА) у Гринвіцькій рухомій системі координат (ГРСК), яка вводиться наступним чином: початок системи відліку у центрі Землі, вісь ОХ лежить у площині екватора та направлена на Гринвіцький меридіан, вісь OZ по осі обертання Землі, вісь OY доповнює систему до правої. Для вимірювання обробки ACH використаємо робастні процедури, за якими БКУ буде проводити (13) 61315 (11) UA (19) реводяться у Кеплерові елементи орбіти (, i, , p, e, ) та порівнюються із прогнозованими значеннями на момент вимірювань. За результатами порівняння робиться висновок про достовірність параметрів і можливості їх використання. Суть запропонованої корисної моделі полягає у наступному: Апаратура супутникової навігації проводить рішення навігаційної задачі та формування вектора  T K g  (KXg, KYg, KZg, KVxg, KVyg, KVzg ) координат U швидкості) переводяться у Кеплерові елементи орбіти (, i, , p, e, ) та порівнюються із прогнозованими значеннями на момент вимірювань, а за результатами порівняння роблять висновок про достовірність параметрів і можливості їх використання. 3 61315 обробку вимірювання, мінімізуючи менш швидко зростаючу функцію - функцію від залишків [3,4]: p n   ˆ (1)   xi   x j   min   i1  j1  або розв'язати систему p n   ˆ ˆ   xi   ijx j  xk  0   (2) i 1  j1  k 1 p ,..., 1 2  x , при x  c; де ( x )   2 c x , при x  c,  (3) Константа с визначає ступінь завадостійкості. Оптимальні значення с знаходяться в інтервалі [, 2 , де  - стандартне відхилення спостережень. Розв'язання системи проводиться, використовуючи стандартні ітераційні процедури ураховуючи характеристики обчислювальних можливостей апаратури супутникової навігації. При використанні координатно - часового способу керування операції на борту можуть виконуватись: в залежності від місцеположення КА(в суворо заданій частині простору); в суворо заданий час; в заданій точці простору та в заданий час. Виходячи з цього планування роботи бортових систем КА може здійснюватись як в структурі "часподія", "координати-подія" та "час-координатиподія". Тому на якість виконання координатних процедур прямо впливає якість навігаційної інформації, інструментом контролю якої є перевірка вірогідності навігаційних вимірюваннь, як наслідок можливі такі ситуації: вимірювання координат ACH достовірні, заданої точності; вимірювання координат достовірні, низької якості через природні причини чи поставлення завад; вимірювання координат недостовірні через природні причини чи поставлення завад; вимірювання координат недостовірні через дезінформацію шляхом випромінювання невірних сигналів навігаційним угрупуванням КА. Доцільним та зручним є контроль відповідності розрахункової орбіти КА спостереження, тобто реальних кеплерових елементів орбіти (, i, , p, e, ) (Фіг. 2), елементам орбіти обрахованим за вимірюваннями ACH. Для обчислення кеплерових елементів орбіти у вимірюванні ACH у ГРСК необхідно зробити перехід від координат у ГРСК у Абсолютну Геоцентричну екваторіальну систему координат ( xГ , yГ , zГг, VXГ , VYГ , VZГ за формулами: 4 x A  cos S  xГ  sin S  yГ   y A  sin S  xГ  cos S  yГ   z A  zГ  (4)  VXA  cos S  VXГ  sin S  VYГ  3  yг  VYA  sin S  VXГ  sin S  VYГ  3  xг    VZA  VZГ  де S - кут, рівний зоряному часу на гринвіцькому меридіані в розглядуваний момент часу. Вважатимемо, що ми маємо обчислені з ГРСК на деякий момент часу при t  t0 координати та проекції швидкості в АГЕСК ( x A0, y A0, zA0, VXA0, VYA 0, VZA0 ) . Для визначення елементів  та і використає мо постійний вектор C (Фіг. 2)моменту кількості руху одиниці маси, який перпендикулярний площині орбіти та рівний подвійній секторній швидкості. Позначимо радіус-вектор та вектор швидкості в  начальний момент відповідно через r та V0 , тоді   C  r  V0 .     r  x A 0 i  y A 0 j  z A 0k Оскільки    V0  VXA 0 i  VYA 0 j  VZA0k то для отримання век тора C на осі АГЕСК отримуємо вирази CX  y A 0 VZA0  z A 0 VYA 0,  CY  z A 0 VXA 0  x A 0ZZA0  (5)  CZ  y A 0 VYA 0  z A 0 VXA 0  а модуль вектора C  C2  C2  C2 X Y Z  Вектор C утворює з віссю Z r кут, рівний на  хилу орбіти i . Тоді проекція вектора C на площину екватора рівна відрізку O3M  C sin i . Якщо вважати, що задані кути , i та модуль C , то для обчислення проекцій вектора на АГЕСК отримаємо наступні вирази: CX  O3M sin  sin i sin    CY  O3M cos  C sin i cos  (6)  Cz  cos i  Оскільки проекції CX, CX, CX та модуль C знайдені раніше по начальних умовах, то ці вирази використаємо для визначення прямого сходження висхідного кута та нахилу орбіти. Нахил і визначаємо з останнього рівняння C cos i  Z , 0  i   . (7) C Для визначення кута  використаємо вирази (6) (7). В результаті отримаємо Cx sin   , c sin i (8) CY cos   , 0    2 . C sin i 5 61315 Перейдемо до визначення елементів, які характеризують геометрію орбіти. Склавши скалярний  добуток векторів r0 та V0 , знаходимо   r0 V0  r0 VA 0 cos( 90  0 )  r0 VA 0 sin 0  x A 0 VXA 0  yVYA 0  zVA 0 , де  0 - кут нахилу вектора начальної швидкості до місцевого горизонту; r0  x 2 0  y 2 0  z2 0 A A A 2 2 2 VA 0  VXA 0  VYA 0  VZA 0 (9) Із співвідношень () отримаємо вираз для визначення кута  0 : sin 0   x A 0 VXA 0  y A 0 VYA 0  z A 0 VZA0 , r0 V0    0  2 2 (10)  Після визначення кута  0 та величин r та V0 фокальний параметр обчислюємо за формулою p  2r00 cos 0 , (11) де 0  2 ro VA0 2k Ексцентриситет орбіти знаходимо, користуючись залежністю e 1 40 (1 0 ) cos2 0 . (12) Значення великої півосі отримуємо з виразу r0  (13) 2(1   0 ) Для визначення аргументу перигею  необхідно ввести в розгляд вектор Лапласу:     r L  VC k . (14) r Вектор Лапласу це постійний вектор, який не залежить від положення центру мас КА на орбіті  dL 0. dL Проекції вектора Лапласу на осі АГЕСК визначаються наступним чином: x A0   r0  Y   L Y  VZA0 ( y A 0 VZA0  z A 0 VYA 0 )  x A 0 ( x A 0 VYA 0  y A 0 VXA 0 )  k A 0  r0  z  L Z  VXA 0 ( z A 0 VXA 0  x A 0 VZA0 )  y A 0 ( y A 0 VZA0  z A 0 VYA 0 )  k A 0  r0   6 L Y cos   L x sin     L cos i (17)  L x cos   L Y sin  cos   ,0    2  L  Далі необхідно визначити час проходження перигею орбіти t, порядок розрахунку буде наступним. Спочатку знаходимо 2 sin 0 cos 0 sin 0  0 , e (18) 20 cos2 0  1 cos 0  , e Далі знаходимо значення E 0 використовуючи залежності: cos 0  e cos E0  , 1  e cos  (19) sin  sin E0  1  e2 . 1  e cos  Знаходимо  за формулою: sin     t0   3 2 (20) (E0  e sin E0 ) , k Тоді на момент видачі параметрів орбіти ACH в деякий начальний момент часу при t  t0 задані координати ( x0, y0, z0, Vx0, Vy0, Vz0 ) Для описання руху по близьких до кругових орбіт в Кеплерових елементах орбіти використовується наступна система рівнянь: d p sin u W , dt K R sin i di p cos u W , dt K R dp p p 2 T, dt K R dq  dt p k sin u  q  cos u   cos u T  W ctgi, S sin u   K R R   dk  dt (21) p q sin u  q  sin u   sin u T  W ctgi,  S cos u   K R  R  3 dt p 2 *  1, du R2 K L x  VYA 0 ( x A 0 VYA 0  y A 0 VXA 0 )  z A 0 ( z A 0 VXA 0  x A 0 VZA0 )  k (15)  Модуль вектора L :  L  L2  L2  L2 X Y Z  Проекції вектора L на осі АГЕСК: L x  L(cos  cos   sin  cos i sin   L Y  L(cos  sin sin  cos i cos   (16)  L z L(sin  sin i  Тому отримуємо наступні два вирази для визначення кута : де R  1 qcosu  k sin u , 1 * 1  , 2 1 KR3 Wctgi sin u u    , q  e cos  , k  e sin , S, T, W - проекції прискорення збурень на напрямки одиничних векторів, K - стала притягання центрального тіла (Землі). j  Ser  Te   W e w , (22) 7 61315 де e r , e  , e w одиничні вектори, направлені відповідно по радіуса, трансверсалі та нормалі до площини оскулюючої орбіти. Нові оскулюючі елементи q і k необхідно ввести через труднощі, пов'язані з визначенням перицентру оскулюючої орбіти. Крім того неможливо встановити залежність між часом t та кутом d  .  , оскільки при e  0 величина dt  e  q2  k 2  Тоді . (23) k   arcsin  e У випадку, коли прискорення збурення S, T, W не залежать явно від часу, то доцільно перейти в цих рівняннях до незалежної змінної u замість t . Для цього необхідно використовувати співвідношення 3 p 2 * (24) 1du R K Тоді рівняння виражені через незалежну змінну u будуть мати наступний вигляд dt  2 2 d sin u * p  1 W, du KR3 sin i 2 di * p  1 cos uW, du KR3 3 dp * p  21 T, du KR3 2 dq * p  1 dt KR2 (25)  k sin u  q  cos u   cos u T  W ctgi, S sin u   R R    2  dk k sin u  q  sin u  * p  1  sin u T  W ctgi,  S sin u   dt R R KR2    В реальних умовах руху КА спостереження прискорення збурення W набагато менше прискорення від центрального гравітаційного поля, при * цьому величина 1 близька до одиниці. При розрахунку її можливо прийняти рівною одиниці без шкоди для точності обчислень. Для розв'язання системи рівнянь (25) для оскулюючих близьких до кругових можна застосувати різні численні методи. Після розв'язання рівнянь (21), (23) можна зробити перехід до змінних e та  . Залежність системи (25) від часу може бути знайдене через диференційний зв'язок p3 2  *du (26) dt  1 R2 K після інтегрування якої отримаємо: 8 t  t0  u p3  R2 u0 2  * du 1 K (27) З результатів моделювання явно бачимо, що значення , e, i на добовому інтервалі майже не змінюються, величина коливань залежить від обраної математичної моделі для розрахунків, тому логічним є закладання даних параметрів в сеансі зв'язку з КА на інтервал планування, прогнозування борту КА u є досить простим (навіть спрощеним інтерполюванням) та не вимагає значних витрат обчислювальних ресурсів КА. Отримання точних начальних умов для прогнозування проводиться за описаною вище робастною процедурою обробки даних ACH. Величини відхилень визначаються та обґрунтовуються при розробці конкретної КС. На основі співставлення обчислених за допомогою ACH та прогнозованих значень кеплерових елементів орбіти робиться висновок про вірогідність вимірювання параметрів руху КА та приймається рішення на використання при відпрацюванні координатних процедур керування вимірювання ACH чи прогнозованих параметрів руху КА Фіг. 3. Джерела інформації 1. Загорулько А.Н. Особенности программных способов управления космическими аппаратами при однопунктной технологии. // Моделювання та інформаційні технології: Збірник, наукових, праць. X.: НАНУ, Інститут проблем моделювання в енергетиці імені Г.Є. Пухова.-2005.- Вип. 32. -С.80-87 2. Бабак В.П., Конін В.В., Харченко В.П. Супутникова радіонавігація.-К.: Техніка, 2004.-328 с 3. Устойчивые статистические методы оценки данных /Пер. с англ. Ю.И.Малахова; Под ред. Н.Г. Волкова. - М.: Машиностроение, 1984.-232 с. 4. Хьюбер Дж. П. Робастность в статистике: Пер. с. англ. - М. Мир, 1984.-384 с, ил. 5. Пат. № 19490 Україна, МПК B64G1/24. Кординатно-часовий спосіб керування космічними апаратами: Пат. № 19490 Україна, МПК B64G1/24. / О.М. Загорулько, В.І. Богомья, О.М. Моргун (Україна). - № и2006 07244; Заявл. 30.06.06; Опубл.15.12.06; Бюл №12.-8с. 6. Теоретичні основи польоту космічних апаратів: Навчальний посібник / В.Є.Бажан, І.Д. Варламов, П.В. Фриз, СП. Фриз/ Під ред. Д.В. П'ясковського. -Житомир: ЖВІРЕ, 2000.-180 с. 9 61315 10 11 Комп’ютерна верстка Г. Паяльніков 61315 Підписне 12 Тираж 24 прим. Міністерство освіти і науки України Державний департамент інтелектуальної власності, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601