Спосіб шліфування ступінчастих валів зі схрещеними осями деталі і круга

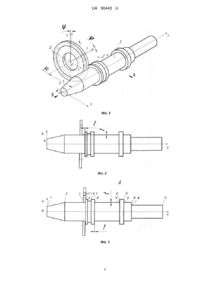
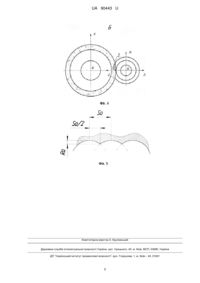
Реферат: UA 90443 U UA 90443 U 5 10 15 20 25 30 35 Корисна модель належить до металообробки та може бути використана при шліфуванні циліндричних ступінчастих валів. Відомий спосіб глибинного круглого шліфування зі схрещеними осями деталі і круга вибрано за аналог (Патент № 47457 Україна, МПК В24В 5/00. Спосіб глибинного швидкісного поздовжнього круглого шліфування зі схрещеними осями деталі та круга / Кальченко В.І., Кальченко В.В., Дмитренко М.А.; опубл. 25.03.2010, Бюл. № 3, 2010). Недоліком цього способу є те, що він призначений тільки для обробки циліндричних поверхонь і не розглядає можливість шліфування торцевих поверхонь зі схрещеними осями круга та деталі. Відомий спосіб глибинного круглого шліфування циліндричних поверхонь зі схрещеними осями деталі і круга та торцевих поверхонь при паралельних осях (А. с. 1234163 СССР, МКИ В24В 5/04. Способ круглого шлифования с продольной подачей. Авт. изобр. В.И. Кальченко. № 3813415/25-08. Заявлено 20.11.84. опубл. 30.05.86. Бюл. № 20. - 4 с.), який прийнято як найближчий аналог. Даний спосіб дає змогу при обробці різних деталей з різними припусками використовувати всю периферію круга. Недоліком даного методу є наявність прижогів на торцевій поверхні через велику площу контакту круга і торця при їх паралельних осях. Задача корисної моделі - підвищення продуктивності і точності шліфування ступінчастих валів і уникання прижогів за рахунок різних кутів орієнтації при обробці циліндричних і торцевих поверхонь. Поставлена задача вирішується тим, що при обробці торцевих поверхонь кут орієнтації круга вибирається з умов отримання необхідної точності, а для циліндричних поверхонь оптимальний кут знаходять з умов потрібної шорсткості, яка описується рівнянням: S  Ra  Pr d0   Pr d o  ,  2  де Pr d0 - висота профілю деталі в точці повороту кута; S  Pr d o  - висота профілю деталі в точці, віддаленій на половину подачі, S o на оберт  2  деталі. На фіг. 1 показано схему глибинного круглого шліфування ступінчастих валів зі схрещеними осями деталі і круга. На фіг. 2 - схема шліфування циліндричної поверхні. На фіг. 3 - вид по стрілці А фіг. 1. На фіг. 4 - вид по стрілці Б фіг. 1. На фіг. 5 - утворення геометричної шорсткості. На фігурах 1-4 вказані позиції: 1 - оброблювана деталь, 2 - шліфувальний круг, 3 - пляма контакту круга і деталі. Схема процесу глибинного круглого шліфування ступінчастих валів зі схрещеними осями інструмента та деталі зображено на фіг. 1, де ступінчастий вал 1 шліфується ельборовим кругом 2. При шліфуванні конусної ділянки 1-2 (фіг. 3) вісь ОuYu, яка співпадає з віссю симетрії круга системи координат OuXuYuZu, розташовується перпендикулярно твірній конусної поверхні, при цьому кут повороту  дорівнює половині кута конусності. Для регулювання площі плями контакту 3 деталі 1 з торцем круга 2 його повертають навколо осі ОuХu на кут  . При поздовжній подачі S  круга 2 після обробки точки 2 (фіг. 3) круг повертається у положення, коли вісь ОuYu перпендикулярна твірній циліндра, тобто   0 . Круг 2 переміщується вздовж осі O Z 40 45 системи координат OXYZ деталі до точки 3, з подачею на оберт S o , а параметр гвинтового руху р дорівнює S p  o . (2) 2 Для розробки загальної модульної 3D моделі зняття припуску та точності формоутворення при шліфуванні ступінчастих валів необхідно описати інструментальну поверхню. Загальна модель інструментальної поверхні шліфувального круга описуються циліндричним модулем, який обумовлюється наявністю таких параметрів: і - координата ділянки шліфувального круга, за допомогою якої задаємо профіль шліфувального круга у площині OuYuZu,  u - кут повороту інструмента навколо осі O uZu (фіг. 1). Загальну модель шліфувального круга можна представити у вигляді ru  Cu i  R i   e 4 , (3) Z u 50 u u де ru - радіус вектор точок шліфувального круга; Cu u i u Ru i  - циліндричний модуль формоутворення шліфувального круга, який являє Z собою матрицю переходу радіус-вектора початкової точки e 4 в систему координат інструмента. 1 UA 90443 U У модульних 3D моделях використовуються однокоординатні матриці М1, М2, М3, М4, М5, М6, які описують переміщення вздовж напрямків Хu, Yu, Zu та повороти навколо осей ОuХu, OuYu, OuZu. Циліндричний модуль, який описує інструментальну поверхню, має вигляд Cui  M3Zu i  M6u   M2Ru i , (4)  5 ru ,i  M3Zu i  M6u   M2Ru i  e 4 . (5) Профіль шліфувального круга запишемо за допомогою функції Хевісайда:   i  ir поч Zu i  i  1  Фi  ir поч    ir поч  r  sin  r     Фi  ir поч   Фi  ir кін   ir поч  r   Фi  ir кін ,      (6)    i  ir поч     1  Ru i  R  1  Фi  ir поч    R  r  cos  r   (7)       Фi  ir поч   Фi  ir кін   R  r  i  ir кін   Фi  ir кін , де ir поч - координата i початку профільної ділянки шліфувального круга; 10 15 ir кін - координата кінця профільної ділянки шліф круга. Використовуємо циліндричний шліфувальний круг прямого профілю з радіусом R радіусом заокруглення r . Номінальна поверхня вала описується радіус вектором шліфувального круга, модулем орієнтації та модулем формоутворення r  Mu  ru  Cф  So  ru , (8)  z   y c де Mu - матриця переходу з системи координат інструмента в систему координат деталі, яка являє собою добуток сферичного модуля S o  орієнтації шліфувального круга щодо  системи координат деталі та циліндричного модуля Cф z   20  y c , який задає рух інструмента відносно деталі. Сферичний модуль орієнтації інструмента дорівнює So   M4   M5  , (9)  Циліндричний модуль формоутворення Cф  M3z   M6   M2yc  , (10) z  yc 25 де y c - міжосьова відстань шліфувального круга і деталі;   - кут повороту деталі; z  - подача, яка описує рух деталі вздовж осі OZ відносно шліфувального круга. Враховуючи формули (3), (8), рівняння обробленої поверхні має вигляд r z,  , ,i  Cф  So  Cu i  R i   e 4 , (11)  Z z   y c 30  p  yc 35 40 u u u Поверхня деталі залежить від 4 параметрів. Тобто треба зв'язати два параметри. Використовуючи параметр гвинтового руху зв'яжемо подачу S o на оберт з кутом повороту деталі використовуючи формулу (2). z    p , (12) враховуючи зв'язок (12) перепишемо рівняння (11) r  , ,i  Cф  So  Cu i  R i   e 4 , (13)  Z u u u Для визначення оброблюваної поверхні необхідно записати рівняння, яке буде визначати лінію контакту деталі та інструментальної поверхні V  n  0 , (14) де n - одиничний вектор нормалі до інструментальної поверхні; V - вектор швидкості відносного руху інструмента в системі координат деталі. Нормаль можна знайти як добуток векторів, дотичних до інструментальної поверхні, тобто для знаходження нормалі необхідно диференціювати радіус-вектор деталі за двома незалежними параметрами   та i . Для знаходження вектора відносної швидкості необхідно радіус вектор інструментальної поверхні в системі координат деталі диференціювати за параметром   , який моделює кут повороту оброблюваної поверхні за одиницю часу. 2 UA 90443 U Отже, при однопараметричному огинанні зв'язок між параметрами u , i,  має вигляд рівності нулю змішаного добутку трьох векторів частинних похідних вектора r .  r r  r , (15)   i       0   u   r r де     n - вектор нормалі до інструментальної поверхні в точці з координатами i та i u 5 10 15 20 u ; r  V - вектор швидкості руху інструмента відносно деталі.  Шорсткість циліндричної поверхні R a (фіг. 5) знаходимо з виразу (1). Необхідна шорсткість забезпечується регулюванням So в залежності від діаметра круга і кута його нахилу. Коли шліфувальний круг підходить до точки 3 - t (фіг. 3), він починає обробляти припуск t торця 3-4 вала. При цьому збільшується пляма контакту 3 і виділення тепла, що негативно впливає на якість обробки, утворюються прижоги. Щоб цього уникнути треба зменшити подачу S o або частоту обертання вала. Оскільки шліфувальний круг повернений навколо осі ОuХu на кут  , тобто осі інструмента і деталі не паралельні, виникає похибка. Після обробки торця 3-4 шліфуємо циліндричні поверхні між точками 4-5, 6-7, 8-9, 10-11, 1213, 14-15, 16-17 та торці ступінчастого вала в напрямку подачі Sд (фіг. 3):7-8, 11-12. Після обробки циліндричної поверхні 16-17 кут нахилу шліфувального круга змінюється на протилежний -  і шліфуємо необроблені торці: 15-16, 13-14, 9-10, 5-6 у напрямку подачі S'д (фіг. 1). При цьому в рівнянні (6) Zu i перед дужками заміняємо знак «+» на «-». Корисна модель може бути застосована майже у всіх галузях машинобудування. ФОРМУЛА КОРИСНОЇ МОДЕЛІ 25 30 Спосіб шліфування ступінчастих валів зі схрещеними осями деталі та круга, який включає використання ельборового круга, вісь якого повернута на певний кут відносно осі деталі, і який здійснює радіальне установче переміщення, при цьому деталь обертається навколо власної осі і переміщується вздовж неї, який відрізняється тим, що при обробці торцевих поверхонь кут орієнтації круга вибирається з умов отримання необхідної точності, а для циліндричних поверхонь оптимальний кут знаходять з умов потрібної шорсткості, яка описується рівнянням: S  Ra  Pr d0   Pr d o  ,  2  де Pr d0 - висота профілю деталі в точці повороту кута; S  Pr d o  - висота профілю деталі в точці, віддаленій на половину подачі, S o на оберт деталі.  2  3 UA 90443 U 4 UA 90443 U Комп’ютерна верстка А. Крулевський Державна служба інтелектуальної власності України, вул. Урицького, 45, м. Київ, МСП, 03680, Україна ДП “Український інститут промислової власності”, вул. Глазунова, 1, м. Київ – 42, 01601 5